螺栓结合面法向静态刚度特性提取方法研究

蔡力钢，郝 宇,2，郭铁能，刘志峰，张冬梅

(1.北京工业大学 机械工程与应用电子技术学院,北京 100022; 2.北京实验工厂，北京 102600)

机械结构中零部件、组件之间接触面即为结合面。结合面存在的接触刚度是机械结构整体刚度的重要组成部分，在力封闭链各联接部件之间若某个结合面接触刚度低，其它构件刚度再高也会失去意义。螺栓联接结合面为机械结构中最典型结合面。螺栓联接具有可靠、强度高、可拆卸、能自锁等优点。螺栓结合面静刚度在载荷作用下具有较强非线性特性，为研究机械系统的重要基础。对螺栓结合面静刚度特性进行的研究对此仍未解决。原因在于机械结合面无厚度，无法直接测量。

曾有研究用内含颜料的微珠敷于螺栓结合面之间，利用受压后微珠破裂颜料扩散，观察染色范围及深浅以估计压力分布范围及趋势。亦曾用压敏材料置于结合面之间检测压力分布规律[1]；但此种试验已改变原结合面状态及性质，因而不能真正反映原结合面特性，且不能做定量分析。Masuko等[2]利用超声波测量结合面压力分布规律，虽不改变原结合面状态，但超声波易受结合面间气隙、介质及金属材料不均匀或组织缺陷等影响，所得压力分布曲线出现无法解释的边缘凸峰，且曲线仅能以超声波回波波高描述压力分布趋势，不能定量分析。姚公棨等[3]分析螺栓结合面特性时采用激光全息摄影与有限元计算结合方法，虽其图像可记录整个板面变形情况，但对试件要求、技术操作、感光材料等均较苛刻，且所得结合面变形为离散的点，不能系统说明结合面静态刚度连续非线性特性变化。

本文舍弃直接求解结合面刚度思想，利用螺栓结合面法向静态刚度、被联接段刚度及螺栓结合部整体静态刚度三者间串联倒数关系，提取螺栓结合面法向静态接触刚度非线性特性曲线。螺栓结合部整体静态刚度通过法向静态拉伸实验方式获得；对计算螺栓结合面被联接段刚度方法进行优化，推导的被联接段刚度的精化解析公式，适用于不同材料、不同尺寸的被联接段。并给出简单易行的螺栓结合面面压计算方法，将所得各数据拟合，获得对应于螺栓结合面面压的螺栓结合面法向静态接触刚度非线性特性曲线。该方法既保持原结合表面特性，亦可进行一定程度的定量分析，且螺栓结合面法向静态刚度连续非线性特性变化得到更直观体现。

1 计算模型处理方法

图1 结合面模型处理方法

将含粗糙面计算模型分成无厚度结合面层及具有相同长度的光滑被联接段[4]，见图1。结合面模型法向刚度K与等长度光滑被联接段法向刚度km均具有可测性，两者差别由粗糙接触表面所致。据无厚度结合面及等长度光滑被联接段法向串联关系，可得法向界面接触刚度kn为

(1)

若已知螺栓结合部刚度K及被联接段刚度km，螺栓结合面刚度kn则不难获得,即

(2)

螺栓结合面结构中螺栓组件主要作用为被联接段及结合面施加法向预紧力，螺栓刚度对求解螺栓结合面法向静态刚度影响不大，求解时可忽略[5-7]。故可用上述方法对螺栓结合面模型进行处理。

2 螺栓结合部静态刚度提取实验

2.1 测试系统与实验装置

鉴于螺栓结合部法向刚度K的可测性，本文设计测试系统获取螺栓结合部刚度K，见图2。试件尺寸及形状由材料试验机卡头特性、应变螺栓尺寸、螺栓预紧力有效范围及拉伸试验机加载方向等特点决定，见图3。

图2 螺栓结合部刚度实验系统

图3 螺栓结合面静态刚度试件装配图及实物图

螺栓结合部法向静态特性测试系统包括材料试验机、螺杆、试件、螺栓、电涡流位移传感器、力传感器、动态应变仪、数据采集系统及计算机。螺栓垂直穿过上、下试件中心的通孔，为螺栓施加一定预紧力，使上下两试件端面相互贴合构成结合面；螺杆与压紧结合面组件同轴心，去除悬臂梁结构对实验结果影响；螺栓预埋的应变片引出导线连接动态应变仪；电涡流位移传感器夹紧在有孔定位法兰上测量电涡流位移传感器与无孔定位法兰间距及螺栓结合部法向位移变化量；上下试件由两螺杆分别与材料试验机连接，通过螺纹部位的旋转使上下两螺杆自动调整合适对正位置，可有效去除试件不对正产生的扭矩；材料试验机搭载力传感器并沿纵向为上、下试件施加静态拉力，可保证试件受力沿轴心方向，力的大小、速率较稳定，易调节。用动态应变仪测量预紧力及螺栓应变信号，用电涡流位移传感器测量结合部法向位移变化量，用力传感器测量静态力信号；三种测量装置将各自信号输出至数据采集系统，并输送至计算机，可获得法向静态拉力数据、法向位移数据。

对螺栓结合面法向静态刚度而言，研究静止状态并非滑动状态，但在法向载荷作用下螺栓结合部仍存在法向微动，造成螺栓结合部法向位移。据刚度计算公式及数学导数相关知识，可推断螺栓结合部法向静态刚度计算式为

(3)

式中：ΔY为螺栓结合部受力改变量；ΔX为螺栓结合部法向位移改变量。

对螺栓结合部所受法向力求导可得与此螺栓结合部所受法向力范围对应的螺栓结合部法向刚度数据。该实验方案各点预压力分布均匀，易控制、调整、测量的物理量个数少，试件易更换及定位，能将结合部刚度特性从实验装置系统特性中分离。

2.2 螺栓结合部刚度提取实验步骤

为提取螺栓结合面法向静态特性曲线，以被联接段厚度相同、结合面间无介质、M16高强螺栓、材料C45粗糙度1.6的工件为例，进行实验与分析。

2.2.1 基础数值

利用材料试验机为试件施加纵向静态力，高强螺栓预紧力10 kN，静态拉力速度 /min，静态拉力终值10 kN。工作时间保持3 min，可得准确数据及合适的实验数据。

2.2.2 位移-外加载荷曲线

数据采集系统处理静态力、位移信号后分别形成一组静态力数据、三组位移数据，并传输PC机。一组静态力数据即外加载荷数据；利用多款数据处理软件(ORIGIN)对三组位移数据进行均值处理，可得一组平均位移数据。利用一组外加载荷数据和一组平均位移数据可得在预紧力10 kN时位移-外加载荷曲线，见图4(a)。

2.2.3 位移-结合面受力曲线

结合面受力=预紧力-外加载荷，通过已知高强螺栓预紧力与外加载荷数据，可得结合面受力数据。利用结合面受力数据与平均位移数据用多种数据拟合方法(六次多项式拟合)可得预紧力10 kN时位移-结合面受力曲线，见图4(b)。

2.2.4 结合面受力-结合部刚度曲线

将所得位移-结合面受力函数关于位移求导，即求图4(b)中每点斜率，并结合每点对应结合面受力，可得合面受力-结合部刚度曲线及结合部刚度数据，见图4(c)。其中结合面受力-结合部刚度曲线由六次多项式拟合获得。

2.2.5 不同预紧力的结合面受力-结合部刚度曲线图

重新设定实验基础数值，改变施加在高强螺栓组件的预紧力分别为20 kN 、30 kN、40 kN、50 kN，材料试验机施加在实验组件的静态拉力速度6 kN/min、9 kN/min、12 kN /min、15 kN/min，静态拉力施加结束值为20 kN、30 kN、40 kN、50 kN。不同实验基础数值下对同一实验组件分别进行相同实验及分析拟合。获得4组不同预紧力的结合面受力-结合部刚度曲线，形成4组不同预紧力下结合部刚度数据，见图4(c)。

2.2.6 实例结合面受力-结合部刚度曲线

对所得5组结合部刚度数据进行处理。结合面受力yi相同结合部刚度ki不同时对ki求平均，即得该实例结合部刚度数据。据结合面受力数据及处理后结合部刚度六次多项式拟合可得修正后结合部刚度函数K。

用结合面受力数据除以结合面有效面积即得结合面面压数据，与结合部刚度数据拟合后可得该实例在多种预紧力时的结合面面压-结合部刚度曲线，见图4(d)。由图4(d)看出，含结合面模型试件总刚度随面压的增大而增大，速率随结合面面压P的增大而减小，与文献[7]结果相符。

(a)(b)(c)(d)

3 被联接段刚度计算方法

为表述简单、计算方便，以结合面位置为界，分别称等长度光滑被联接段上、下两部分为上、下被联接段。Lehnhoff等[5]提出的简单有效螺栓结合面分析模型见图5，并利用有限元分析、计算被联接段刚度。分析计算中设垂直螺栓结合面方向压应力均匀分布，大小随z向位置变化而变化，压应力分布呈截头圆锥体，见图6。

图5 螺栓结合面模型

组成结合部上、下试件为同材料、同厚度时螺栓联接的单个被联接段截头圆锥体刚度kmi的计算式为

(4)

该螺栓被联接段整体刚度为

式中：γ为螺栓接触直径比率；d为螺栓直径；α为截头圆锥体半锥角；E为被联接段材料弹性模量；L为单个被联接段截头圆锥体厚度。

由式(4)看出，此计算被联接段刚度方法涉及参数数量较少且易确定，在保证一定精度前提下，使被联接段刚度计算简单实用。但需注意的是，① 计算时应选螺栓孔直径d0而非螺栓直径d；② 式(4)中γd指螺栓接触直径，在给定螺栓组件中螺栓接触直径即为螺栓组件垫片外直径d1；③ 式(4)只适用计算同种材料的被联接段刚度，具有一定局限性。

针对①、②，式(4)应修改为

(5)

式中：kmi为单个被联接段刚度；d0为被联接段螺栓孔直径；d1为螺栓垫片外径；α为截头圆锥体半锥角；Ei为被联接段材料弹性模量；Li为截头圆锥体厚度。

针对③，设螺栓预紧力为F；上下被联接段刚度分别为km1，km2；其z向变形分别为δ1，δ2。据胡克定律有km1=F/δ1，km2=F/δ2。被联接段z向总变形[6]δ=δ1+δ2，其整体刚度为

(6)

将式(5)所得km1，km2代入式(6)便得螺栓结合面被联接段整体刚度km，可用于不同材料、不同尺寸的被联接段。

图7 螺栓结合面静态刚度实例被联接段等效模型

由图7知，d0=18×10-3m，d1=33×10-3m，d=16×10-3m，E1=E2=200×109，L1=L2=20×10-3m，利用定锥角法刚度公式[5]确定半锥角α=30°。由于上下被联接段厚度、材料相同，故km1=km2。据式(6)得实例被联接段刚度为

6.15×109(N/m)

4 螺栓结合面刚度提取

以所得实例结合部与被联接段刚度数据利用式(3)可得结合面刚度。数据拟合的实例面压-结合面刚度曲线见图8，该曲线亦为螺栓结合面法向静态特性曲线。由图8看出，结合面面压小于5 MPa时，结合面法向接触刚度与结合面面压成非线性关系，并随其增大而增大；结合面面压大于5 MPa时，结合面刚度值增大缓慢甚至不增加。所得结果与其它实验所得结合面特性规律[9]及结合面微观分形理论[10]一致。表明该提取螺栓结合面法向静态刚度方法的可靠性与正确性，在保持原结合表面的特性情况下能容易进行定量分析，且直观体现一定条件下螺栓结合面法向静态刚度连续非线性特性变化。

图8 螺栓结合面法向静态特性曲线

5 螺栓结合面有效作用面积确定

通过对被联接段刚度计算可知，螺栓联接结合面有效作用面积并非接触面积，为压应力截头圆锥体分布在结合面的投影面积。因而需注意被联接段上下试件厚度对结合面有效作用面积影响。两试件厚度相同时，上下试件所受压应力的截头圆锥体分布在结合面的投影面积相同，取其一作为螺栓结合面有效作用面积即可；两试件厚度不同时上下试件所受压应力的截头圆锥体分布在结合面上的投影面积不同，应选投影面积较小者为结合面有效作用面积。

螺栓结合面接触面积形状大小对结合面有效作用面积亦有影响。分别以圆形、方型两种最基本的结合面接触面积为例，描述上下试件厚度相同、不同时各螺栓结合面的有效作用面积，见表1、表2。为计算其它形状结合面接触面积有效作用面积奠定理论计算基础。由表1知，该实例上下被联接段厚度相同L1=L2，结合面接触面外径R>d2/2。则结合面有效作用面外径为

d2=d1+Ltanα=33×10-3+40×10-3tan30°=

56.09×10-3(m)

其有效作用面积为

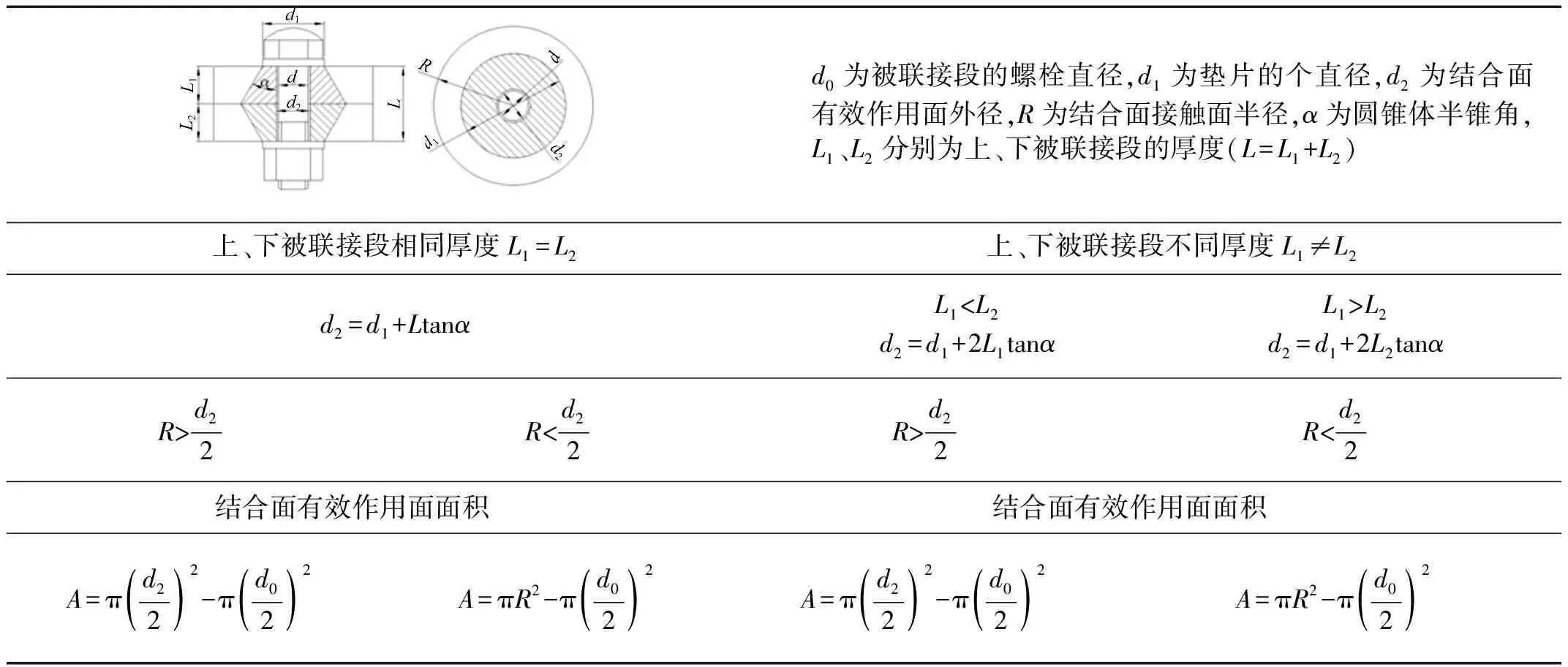
表1 圆形结合面接触面积

表2 方形结合面接触面积

6 结 论

(1) 本文据螺栓结合面法向静态刚度、被联接段刚度及螺栓结合部刚度三者间串联倒数关系，提出提取螺栓结合面法向刚度新方法。通过法向静态拉伸实验及理论分析结合方式，将螺栓结合面法向静态接触刚度非线性从螺栓结合部整体静态刚度模型中分离；并对计算螺栓结合面被联接段刚度方法进行优化，推导出新的被联接段刚度计算公式，可用于不同材料、不同厚度计算。

(2) 提出的确定螺栓结合面有效作用面积方法，能完整提取螺栓结合面法向静态接触刚度非线性特性曲线。并用实例验证其可靠性与正确性。

(3) 结合本文提取螺栓结合面法向静态刚度方法，通过改变螺栓结合面各种结合条件(结合面材质、加工方法、加工质量、结合面间介质等)，可进一步研究各种不同基本结合因素对螺栓结合面静态刚度影响。

[1] Yu Hong-rong, Wu Yong-li, Li Guo-chen. Plane strain asymptotic fields for cracks terminating at the interface between elastic and pressure-sensitive dilatant materials[J]. International Journal of Fracture,1997, 86(4): 343-360.

[2] Minakuchi Y．Measurement of contact pressure by means of ultrasonic waves[J]．Bulletin of JSME,1985,28(239):792-798.

[3] 姚公棨,赵汝嘉,陶钟．全息摄影在机械结合面特性研究中的应用[J]．应用激光,1989,9(6)：263-266．

YAO Gong-qi, ZHAO Ru-jia, TAO Zhong. Application of holography in the study on the characteristics of mechanical joints[J]. Laser Journal, 1989,9(6):263-266．

[4] 李辉光,刘恒,虞烈.粗糙机械结合面的接触刚度研究[J].西安交通大学学报,2011,45(6):69-74．

LI Hui-guang, LIU Heng,YU Lie. Contact stiffness of rough mechanical joint surface[J]. Journal of Xi’an Jiaotong University, 2011,45(6):69-74．

[5] Lehnhoff T F, Ko K II, Mckay M L. Member stiffness and contact pressure distribution of bolted joints[J]. Journal of Mechanical Design, 1994, 116(2): 550-557.

[6] 杨国庆,王飞,洪军,等．螺栓被连接件刚度理论的计算方法[J]．西安交通大学学报,2012,46(7): 50-56．

YANG Guo-qing, WANG Fei,HONG Jun, et al. Theoretical analysis for bolted member stiffness [J]. Journal of Xi’an Jiaotong University, 2012, 46(7): 50-56．

[7] Nassar S A. An improved stiffness model for bolted joints[J]. Journal of Mechanical Design, 2009,131:121001.1-121001.11．

[8] 黄玉美,佟竣贤,秦世良.机床结构设计效果预断中结合条件的处理方法[J]机床,1990(6): 8-12．

HUANG Yu-mei,TONG Jun-xian,QIN Shi-liang. Method of prcessing joining condition in predicting the result of machine tool structural design[J]. Machine Tool,1990(6):8-12．

[9] Toshimichi F, Masataka N, Nobukuni S. Experimental investigation and finite element analysis of the free vibration problem of bolted joint by taking account of interface stiffness[J]. Journal of Environment and Engineering,2009, 4(1):101-111.

[10] 张学良．机械结合面动态特性及应用[M]．北京：中国科学技术出版社,2002．