多跨体外预应力连续梁动力特性研究-模态解析解
石鲁宁,闫维明,何浩祥,陈彦江
(北京工业大学 工程抗震与结构诊治北京市重点实验室,北京 100124)
结构动力特性的重要指标为频率、振型,对其进行数值求解或求得解析表达具有重要工程意义。现有求解方法主要有两类,即离散方法与连续方法。前者将结构视为多自由度离散体系,其计算精度取决于结构离散自由度数量;后者将结构视为分布参数体系,建立无限自由度体系运动方程,将模态参数求解归结为超越方程问题求解。对简支梁等简单结构,连续方法可求得解析解[1-2],但连续梁等复杂结构解析解较难求得;连续梁有预应力作用时,预应力与模态参数关系较难确定,仅依靠有限元方法对具体结构求解无法获得规律性结果。因此需研究多跨预应力连续梁模态解析解。Ayaho等[2]研究体外预应力加固组合梁的动力特性,推导出双折线形式体外预应力简支梁振动方程,并分析预应力及预应力钢筋转角等参数对组合梁自振频率影响。Hamed等[3]通过试验研究有、无粘结预应力对简支梁自振频率影响。Hamed等[4-5]研究带裂缝预应力梁的动力特性,分析轴向力对频率振型影响。宗周红等[6]通过试验研究预应力对混凝土简支梁动力特性影响。方德平等[7]用能量法分析体外预应力对简支梁动力特性影响。Li[8]基于渐进Timoshenko梁理论研究轴向荷载作用下弹性支承及梁段集中质量剪切梁的振动特性。以上研究均未考虑预应力对连续梁动力特性影响。Luo[9]研究轴向力作用下无限长等间距支承梁的横向振动问题,分析不同轴向载荷对梁振动特性影响。王小岗等[10-11]利用狄拉克函数建立的多跨连续梁振动方程求解异常复杂,工程实践中较难普及。熊学玉等[12]研究两等跨体外预应力连续梁动力特性,引入狄拉克函数建立两跨连续梁振动方程,而求解三跨及三跨以上连续梁振动方程较困难,且未给出具有普遍意义多跨体外预应力多跨连续梁的频率方程解析解。
关于三跨及三跨以上预应力连续梁振动特性研究多限于数值模拟,理论研究尚不成熟。本文基于Ayaho等[2,12]理论研究方法,据多跨预应力连续梁结构特点及力法基本原理建立体外预应力变化量与位移的函数关系,将连续梁视为满足边界条件的多个单跨梁,采用分段联立方法建立多跨体外预应力连续梁振动方程组,简化预应力连续梁振动方程求解,求得多跨预应力连续梁频率方程与多跨体外预应力连续梁自振频率及振型。
1 多跨预应力连续梁振动方程
1.1 预应力简支梁振动方程
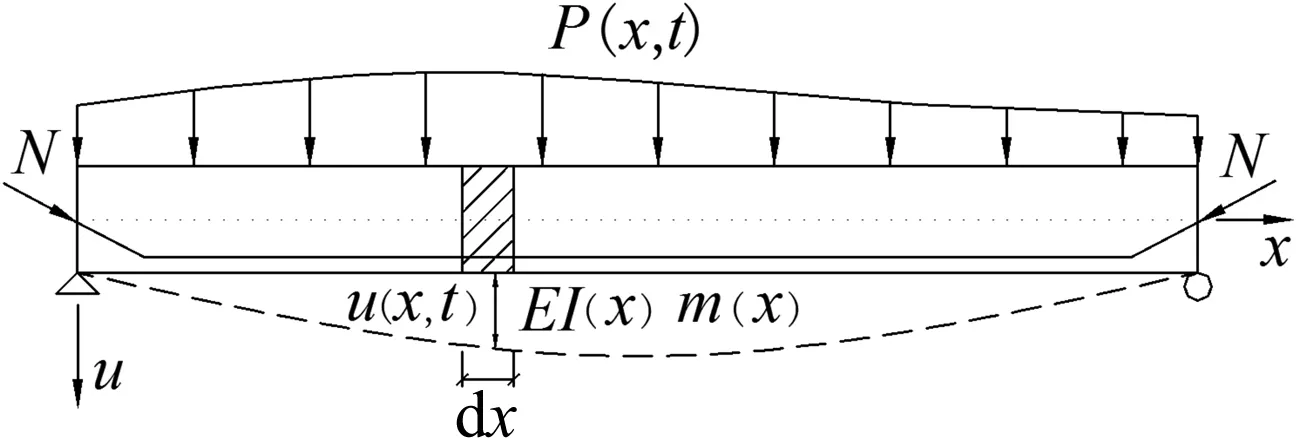
图1 受动力荷载体外预应力简支梁
非均匀预应力简支梁见图1,沿梁长x方向变化的等效抗弯刚度为EI(x),单位长度质量为m(x),作用于梁上预应力为N。梁横向荷载P(x,t)及横向位移μ(x,t)随位置、时间任意变化。设梁的运动为平面弯曲,预应力N沿x向无损失,简支梁在预应力作用下弯曲振动方程[2,12-13]为
(1)
式中:Nx为预应力N水平分量;ΔN为随振动位移变化所致预应力改变量;H为预应力钢筋等效偏心距,预应力钢筋在不同梁横截面位置上偏心距不相同,需按弯矩图面积相等原则计算。
1.2 多跨预应力连续梁振动方程
n(n≥2)跨预应力连续梁材料为均匀、连续各向同性且变形满足平面假,见图2。设第i跨等效抗弯刚度为EIi(x),单位长度质量为mi(x),作用于第i跨上预应力为Ni,横向荷载为Pi(x,t),梁的横向位移为μi(x,t)。

图2 受动力荷载多跨预应力连续梁
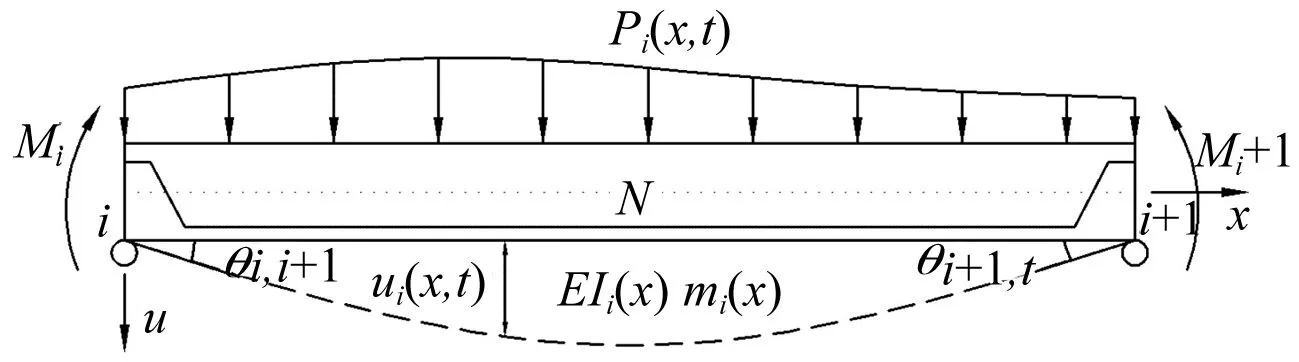
图3 受动力荷载第i跨梁段
以第i跨梁段为研究对象,见图3。设第i跨梁段起点i的转角为θi,i+1,弯矩为Mi,i+1,终点i+1处转角为θi+1,i,弯矩为Mi+1,i。第i跨振动方程为
(2)
多跨预应力连续梁第i(1≤i≤n)跨自由振动方程为
(3)
第i(2≤i≤n-1 )跨梁段与相邻跨弯矩、转角需满足:
(4)
首跨及末跨与其相邻跨弯矩、转角需满足:
(5)
等截面多跨预应力连续梁第i(1≤i≤n)跨自由振动方程可简化为
(6)
显然,n跨预应力连续梁振动方程为满足弯矩、转角条件的n个单跨振动方程组成的方程组。本文公式推导以等截面多跨体外预应力连续梁为例。为求解多跨预应力连续梁自由振动方程组需先求得振动过程中预应力变化量ΔN与梁体振动位移μ(x,t)之关系。
1.3 预应力变化量与梁位移关系
多跨体外预应力连续梁在自由振动过程中预应力变化量ΔN随梁体振动位移μ(x,t)变化而变化,梁体自由振动处于小变形状态,几何变形上可近似认为预应力变化量ΔN与梁体竖向振动位移μ(x,t)成正比[2,12]。设跨中作用集中力F,先求F与ΔN关系,再求F与μ(x,t)关系,由代换求ΔN与μ(x,t)关系。

图4 连续梁边跨简化模型及内力图
多跨预应力连续梁边跨(i=1、n)近似简化结构见图4。设梁跨中作用集中力F,将预应力变化量与中间支座弯矩作为多余未知力X1,X2,去掉多余联系获得基本体系,求单位力X1=1,X2=1及集中力F作用下弯矩图(图4)。建立变形协调方程为
(7)


由式(7)解得:
(8)
边跨梁段在跨中集中力F作用下,跨中竖向位移μF为
(9)
整理式(8)、(9)得ΔN与μF关系为
(10)
梁体内预应力钢筋产生的次内力作用使预应力产生改变量ΔN,而次内力作用使梁段产生与μF方向相反的竖向位移μΔN。求出边跨次内力产生的竖向位移μΔN为
(11)
边跨梁段在F作用下产生的竖向位移μ为
μ=μF-μΔN
(12)
将式(10)、(11)代入式(12)整理得:
ΔN=φμ
(13)

(14)

图5 连续梁中间跨简化模型及内力图
多跨预应力连续梁中间跨(2≤i≤n-1)可近似简化为图5结构。设梁段跨中作用集中力F,将预应力变化量与支座弯矩作为多余未知力X1,X2,X3,求得单位力X1=X2=X3=1及集中力F作用下弯矩图(图5),建立变形协调方程为
(15)
式中:δij,ΔiF按式(7)计算。由式(15)解得:
(16)
式中:

中间跨梁段在F作用下竖向位移μF为
(17)
中间跨梁段在F作用下由次内力产生的竖向位移μΔN为
(18)
中间跨梁段在F作用下产生的竖向位移μ与预应力变化量ΔN的函数关系式同式(12)。同理求得:

(19)
1.4 等效偏心距求解
H为等效偏心距,将预应力作用弯矩按面积相等原则等效为沿梁长均布求得H[2,12]。由图5可求得中间跨预应力效应引起的弯矩MN为
(20)
MN弯矩图面积为
(21)

由式(21)得:
(22)
同理,由图4可求得边跨等效偏心距H为
(23)
将式(14)、(19)代入式(6)可得多跨体外预应力连续梁自由振动方程组为
(24)
2 多跨预应力连续梁频率及振型
2.1 振动方程求解
文献[7,12,14]利用狄拉克函数建立的连续梁振动方程不易求得三跨及以上连续梁频率方程,因此本文将多跨预应力连续梁振动方程求解转化为满足弯矩、转角条件的多个单跨振动方程求解,且可方便获得频率方程。据式(24)多跨体外预应力连续梁第i跨振动方程可化简为
(25)
该方程采用分离变量法求解[13,15],设定解形式为
ui(x,t)=φi(x)Y(t)
(26)
将解的形式代入式(32)得:
φ″″i(x)+g2φ″i(x)-a4φi(x)=0
(27)
Y″(t)+ω2Y(t)=0
(28)

式(27)为四阶常系数微分方程,设解的形式为Φi(x)=Gesx,代入方程得:
s1,2=±ihi,s3,4=±ini
(29)
式中:

代入Φi(x)=Gesx得方程通解为
φi(x)=G1eihix+G2e-ihix+G3enix+G4e-nix
(30)
式中:G1,G2,G3,G4为复常数。
用三角函数、双曲函数等价替换指数函数,并令式(30)中虚部为零,得:
φi(x)=Asin(hix)+Bcos(hix)+
Csinh(nix)+Dcosh(nix)
(31)
式中:A,B,C,D为实常数,可由梁端边界条件(位移、转角、弯矩等)求出,从而获得预应力梁自振频率及振型。
2.2 振型方程求解
图3中第i(1≤i≤n)跨梁段两端位移、弯矩需满足:
(32)
利用式(31)及对x二阶偏导数,由式(32)求得:
(33)
将系数A,B,C,D代入式(31)可得第i(1≤i≤n)跨振型函数表达式。
2.3 频率方程求解
第i(1≤i≤n)跨梁段由振型函数式(33)微分一次得转角方程:
θi(x)=[Mi+1,i-Mi,i+1cos(hiLi)]cos(hix)-
[Mi+1,i-cosh(niLi)Mi,i+1]cosh(nix)-
Mi,i+1sin(hiLi)sin(hix)-
Mi,i+1sinh(niLi)sinh(nix)
(34)
式中:
因Mi=Mi,i+1=Mi,i-1,支座i(2≤i≤n)两侧转角为
θi,i+1=[ψicosh(hiLi)-
ηicos(hiLi)]Mi-(ψi-ηi)Mi+1
(35)
θi,i-1=(ψi-1-ηi-1)Mi-1-[ψi-1cosh(ni-1Li-1)-
ηi-1cos(hi-1Li-1)]Mi
(36)
n跨连续梁相邻两跨转角需满足θi,i-1=θi,i+1,其中2≤i≤n,由式(35)、(36)得:
Xi-1Mi-1+(Yi-1+Yi)Mi+XiMi+1=0
(37)
式中:Xi=ψi-ηi;Yi=ηicos(hiLi)-ψicosh(niLi)。
以上方程组共有n-1个方程、n+1个未知数,整理成矩阵形式为
CM=0
(38)
式中:M=[M1,M2,…,Mn+1]T
n跨连续梁需满足M1=Mn+1=0,整理式(38)得:
C0M0=0
(39)
式中:M0=[M2,M3,…,Mn]T
式(39)系数矩阵为稀疏带状矩阵;n跨预应力连续梁在任意激励下式(39)必存在非零解,且恒成立:

(40)
式(40)即n跨体外预应力连续梁频率方程。通过计算可得该方程前n个正根,即该n跨体外预应力连续梁竖向前n阶频率。n跨体外预应力连续梁横向振动频率按本文方法可同样求得,参数φ,H为考虑预应力钢筋横向作用效应时求得。由式(40)可得两跨体外预应力连续频率方程为
η1cos(h1L1)-ψ1cosh(n1L1)+
η2cos(h2L2)-ψ2cosh(n2L2)
(41)
三跨体外预应力连续梁频率方程为
[η1cos(h1L1)-ψ1cosh(n1L1)+
η2cos(h2L2)-ψ2cosh(n2L2)]×
[η2cos(h2L2)-ψ2cosh(n2L2)+η3cos(h3L3)-
ψ3cosh(n3L3)]-[ψ2-η2]2=0
(42)
3 公式、试验与有限元分析
3.1 两跨体外预应力连续梁频率方程验证
文献[16]对一矩形截面体外预应力两跨连续梁进行试验,并测得自振频率。试验梁高0.36 m,宽0.17 m,材料弹性模量用实测值2.68×104MPa,预应力钢筋弹性模量为1.98×105MPa,预应力钢筋用2根1860级φ15.2钢绞线,每根预应力钢绞线有效预应力为140 kN,计算跨度(4.3+4.3) m。由式(41)所得自振频率及试验梁自振频率、实测频率及有限元结果[12]见表1。
由表1知,本文公式计算所得两跨体外预应力连续梁基频与试验结果吻合较好;与有限元及文献[12]计算连续梁基频及有限元结果相对误差分别在2.62%,2.9%以内,从而验证本文利用分段联立方法建立多跨体外预应力连续梁动力方程及所得的频率方程的正确性;利用本文方法所求两跨体外预应力连续梁自振频率具有足够精度。本文方法亦可求解多跨体外预应力连续梁自振频率。

表1 两跨体外预应力连续梁自振频率公式、试验及有限元结果
3.2 三跨体外预应力连续梁频率方程验证
利用推导的三跨体外预应力连续梁频率方程式(42)求解三跨体外预应力连续梁自振频率及振型,并与有限元分析结果对比。三跨体外预应力连续梁见图6,高1.0 m,宽0.7 m,计算跨度(10+ 16+10)m;混凝土等级C35;预应力钢筋为4根1860级φ15.2钢绞线,每根预应力钢绞线有效预应力140 kN,预应力钢筋布置简化为多折线形式。

图6 三跨体外预应力连续梁示意图
求解式(42),频率方程根分布情况见图7,三跨体外预应力连续梁前四阶振型见图8,三跨体外预应力连续梁自振频率、有限元结果见表2。

图7 三跨体外预应力连续梁频率方程根分布

图8 三跨体外预应力连续梁振型图

表2 三跨体外预应力连续梁分析结果
由表2知,本文方法所求三跨体外预应力连续梁基频与有限元结果相对误差为1.22%,连续梁前四阶频率与有限元分析结果平均误差在3%内,满足工程需要。利用本文推导方程可准确求得结构动力参数、有效指导工程实践。
4 结 论
(1) 详细推导多跨体外预应力连续梁的振动方程,给出多跨体外预应力连续梁频率方程解析解。
(2) 给出多跨体外预应力连续梁振动过程中预应力变化量ΔN与位移μ(x,t)关系计算式及等效偏心距H计算式。
(3) 对两、三跨体外预应力连续梁,本文公式计算结果与文献[12]、实测及有限元结果吻合较好;验证本文推导的多跨体外预应力连续梁频率方程的正确性。本文公式也适用三跨以上体外预应力连续梁动力参数求解,将本文理论成果编写程序予以推广,可有效指导工程实践,具有重要工程意义。
(4) 本文基于Bernoulli-Euler梁理论推导的多跨体外预应力连续梁的振动方程适用于梁挠度远小于梁长度情况,且计算精度足够。
[1] Piersol H. Harris’ shock and vibration handbook (fifth edition)[M]. New York: McGraw-Hill,2002.
[2] Miyamoto A,Asce M,Tei K,et al. Behavior of prestressed beam strengthened with external tendons[J]. Journal of Structural Engineering, 2000, 126(9):1033-1044.
[3] Hamed E, Frostig Y. Natural frequencies of bonded and unbonded prestressed beams-prestress force effects[J]. Journal of Sound and Vibration, 2006, 295(1/2):28-39.
[4] Hamed E, Frostig Y. Free vibrations of cracked prestressed concrete beams[J]. Engineering Structures, 2004, 26(11):1611-1621.
[5] Binici B. Vibration of beams with multiple open cracks subjected to axial force[J]. Journal of Sound and Vibration, 2005, 287(1/2):277-295.
[6] 夏樟华,宗周红. 预应力对混凝土梁动力特性的影响分析[J]. 振动与冲击,2007, 26(7):129-134.
XIA Zhang-hua,ZONG Zhou-hong. Analysis of influence of prestressing on dynamic characteristics of a concrete beam[J]. Journal of Vibration and Shock, 2007, 26(7): 129-134.
[7] 方德平,王全凤. 体外预应力梁动力特性的能量法分析[J]. 振动与冲击,2012,31(1):177-181.
FANG De-ping, WANG Quan-feng. Dynamic behavior analysis of an externally prestressed beam with energy method[J]. Journal of Vibration and Shock, 2012, 31(1):177-181.
[8] Li X F. Free vibration of axially Loaded shear beams carrying elastically restrained lumped-tip masses via asymptotic Timoshenko beam theory[J]. Journal of engineering mechanics, 2013,139(4):420-426.
[9] Luo Yan-yun. Frequency analysis of infinite continuous beam under axial loads[J].Journal of Sound and Vibration, 1998, 213(5):791-800.
[10] 王小岗.简谐激励下多跨连续梁振动问题的解析解[J]. 青海大学学报,1996, 14(4):31-36.
WANG Xiao-gang. Analytical solution of the vibration of simple harmonic excitation of continuous beam[J]. Journal of Qinghai University,1996,14(4):31-36.
[11] 李吉.求解多跨连续梁固有振动精确解的一种方法[J]. 力学与实践,1992, 14(2):27-29.
LI Ji. Anexact solution of multi-span continuous beam natural vibration[J]. Mechanics and Engineering, 1992, 14(2): 27-29.
[12] 熊学玉,高峰,李阳. 体外预应力连续梁振动特征的分析与研究[J]. 振动与冲击,2011, 30(6):104-108.
XIONG Xue-yu, GAO Feng, LI Yang. Analysis on vibration behavior of externally prestressed concrete continuous beam[J]. Journal of Vibration and Shock, 2011, 30(6):104-108.
[13] 刘晶波,杜修力. 结构动力学[M]. 北京:机械工业出版社, 2005: 122-156.
[14] Hosking R J,Husain S A, Milinazzo F. Natural flexural vibrations of a continuous beam on discrete elastic supports[J]. Journal of Sound and Vibration, 2004, 272(1/2):169-185.
[15] Penzien C. Dynamics of structure[M]. New York: Computers and Structures,2011.
[16] 郑玉庆,卜伟筠,周海浪,等.体外预应力梁的振动问题的研究分析[J].四川建筑科学研究,2002,28(3): 75- 78.
ZHENG Yu-qing, BU Wei-yun,ZHOU Hai-lang,et al. Vibration models analysis of prestressed concrete beam with external tendons[J]. Building Science Research of Sichuan, 2002, 28(3): 75-78.

