First-principles calculation of electronic properties of N- and X(X=S,Se,Te)-codoped anatase TiO2

LI Chang-sheng, REN Jun, GUO Hai-yan，PENG Xing，WANG Jian-long, CAO Duan-lin

(School of Chemical Engineering and Environment, North University of China, Taiyuan 030051, China)

TiO2(titanium dioxide) has attracted intensive attention due to its extensive applications in decomposition of organic pollutants, solar cells and photoelectrochemical splitting of water[1,2].However, as a wide band gap semiconductor (3.20 eV), anatase allows only absorption of ultraviolet irradiation, which amounts to 3% of solar energy.Only about 5% of the solar spectrum can be utilized due to its wide intrinsic band gap.Furthermore, its photo-excited electron-hole pairs recombine relatively easily.Therefore, it is of great interest to find ways to extend absorption wavelength range of TiO2in the visible region without decreasing the photocatalytic activity.

Generally speaking, impurity doping is usually one of the typical approaches to adjust the band gap in the visible region.Research indicates that doping metals and non-metals can obviously narrow the forbidden gap to improve effective photocatalytic performance[3-9].Extensive studies have proposed that N-doped TiO2is a promising photocatalytic material[10,11].Umebayashi et al.[8]indicated that in the visible region, S-doping caused the absorption edge of TiO2to shift into the lower energy region.Theoretical analysis shows that using ab initio calculations, mixing of S 3p states with the valence band contributes to the band gap narrowing.However, S-doped TiO2can narrow the band gap, but it is difficult for S-doped TiO2to achieve it due to large formation energies required for substituting S for O in TiO2[7].So it is important to study the photocatalytic application of S-doped TiO2.For the Se-doped study, Jenks et al[12]indicated that the Se-modified TiO2displayed greater visible absorption than undoped TiO2under ultraviolet (UV) light.Gurkan et al[13]indicated that, for Se(IV)-doped TiO2, the experimental results manifested that there is a high visible light absorption from 420 nm to 650 nm.Combined with density functional theory (DFT) calculations, Se(IV)-doped TiO2enhances the photocatalytic activity by introducing the additional electronic states originating from the Se 4p orbit in the band gap.However, there is no reported theoretical work focusing on the synergistic effect of Te-doped anatase TiO2.

On the basis of DFT for the chalcogen elements mono-doped TiO2, there are some researches about N- and X(X=S, Se, Te)-codoped anatase TiO2.GAO et al.[14]indicated that the experimentally observed absorption edges of (N, S)-codoped TiO2are 420, 413, and 429 nm, respectively.DFT calculations explained that N doping leads to the narrowed energy gap with the optical absorption shifting to the red region and S-doping introduces impurity states between the conduction band and the valance band.Behpour et al.[15]confirmed that N and S lead to less grain size, the red shift in optical absorption wavelength to visible region has high photocatalytic activity by different detected measurements.However, there is no reported theoretical work focusing on the synergistic effects of (N,Se)- and (N, Te)-codoped anatase TiO2on the mechanism of band-gap narrowing about substituting O and Ti.Our study focuses on the electronic properties of the N- and/or X(X=S, Se, Te)-doped anatase TiO2using DFT calculations.In this paper, we try to study the cooperative role of N and X(X=S, Se, Te)-codoped TiO2on the mechanism of band-gap reduction of TiO2.

1 Computational methods and models

All of the spin-polarized calculations were performed using the projector augmented wave (PAW) pseudopotentials for implementation in the Vienna ab initio simulation package (VASP) code[16,17].The Perdew-Burke-Ernzerhof parametrization[18]of the generalized gradient approximation[19]was adopted for the exchange-correlation potential.The electron wave function was expanded in plane-wave up to the cutoff energy of 420 eV and the optimized lattice constants agreed well with the experimental values.The calculations of optimized geometry and electronic properties were carried out, using the block Davidson scheme[20,21]for geometry optimization.The Brillouin-zone integrations were performed using Monkhorst-Pack grids[22].A 4×4×1k-mesh was used for optimization of geometry and a substantially denserk-mesh of 8×4×2 was used for substitution energies, and electronic properties calculations due to 2×2×2 anatase supercell was used in this study.The supercell model is shown in Fig.1.

To overcome the well-known underestimated band gap problem of the metal oxides in 3d electrons, The DFT + U[23]approach introduces an on-site correction in order to describe the system with localized d and f electrons, which can produce better band gaps in comparison with experimental results.Here, effective on-site Coulomb interactionsU(U=U′-J) for Ti 3d were used to obtain the correct band gap.U′ andJrepresent the energy cost of adding an extra electron at a particular site and the screened exchange energy, respectively.Here,U=6.2 eV was used on Ti 3d electrons.Although the DFT+U approach yields a more accurate band gap, the accuracy in thermodynamic predictions and optimized cell parameters was reduced, owing to dependence on the effective U parameter[24].Therefore, we use DFT+U method for the calculations of structural optimization, substitution energies and electronic structure.

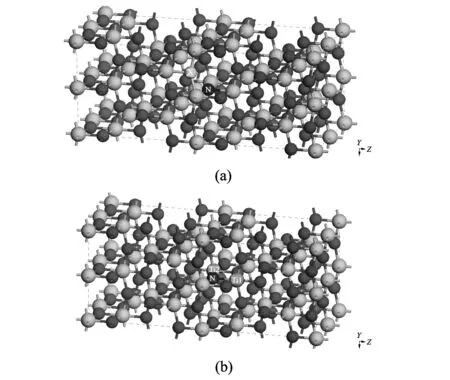
Fig.1 Supercell model for N and X(X=S, Se, Te)-codoped 96-atom anatase TiO2, showing the location of the dopants for (a) and (b).The ion doping sites are marked with N, X, Ti1 and Ti2.

2 Results and discussion

2.1 Geometry analysis

After structural optimization of pure anatase TiO2, the optimized lattice parameters area=b=3.842 Å,c=9.625 Å, which are in good agreement with the experimental values,a=b=3.787 Å,c=9.502 Å[25], as well as the theoretical results,a=b=3.880 Å,c=9.681 Å[26].The result demonstrates that the computational methods adopted in this paper are reasonable and reliable.

The optimized lattice parameters for pure TiO2, as well as N- or/and X(X=S, Se, Te)-doped anatase TiO2are summarized in Table 1 and Table 2, respectively.

Table1Calculatedlatticeparametersa,b,candVofpure,N-,S-,Se-,Te-dopedand(N,S)-, (N,Se)-, (N,Te)-codopedanataseTiO2forsubstitutingOforNandX(X=S,Se,Te).TheexperimentaldataandtheoreticalresultsarelistedforcomparisonwithGGA+Umethod

a(Å)b(Å)c(Å)V(Å3)Pure TiO2(This work)7.7417.74119.3431 159.09Pure TiO2(Experimen-tal[25])7.5647.56419.0041 087.30Pure TiO2(Theoretical[26])7.7617.76119.3621 166.23N-doped TiO27.7467.75819.3011159.86S-doped TiO27.7387.80419.3311 167.35Se-doped TiO27.7347.82319.3371 169.95Te-doped TiO27.7347.82019.4611 177.00(N, S)-codoped TiO27.7617.75219.3901 166.57(N, Se)-codoped TiO27.7677.75819.4061 169.34(N, Te)-codoped TiO27.7757.76119.4361 172.80

Table2Calculatedlatticeparametersa,b,candVofpure,N-,S-,Se-,Te-dopedand(N,S)-, (N,Se)-and(N,Te)-codopedanataseTiO2forsubstitutingTiforX(X=S,Se,Te)andOforN.TheexperimentaldataandothertheoreticalresultsarelistedforcomparisonwithGGA+Umethod

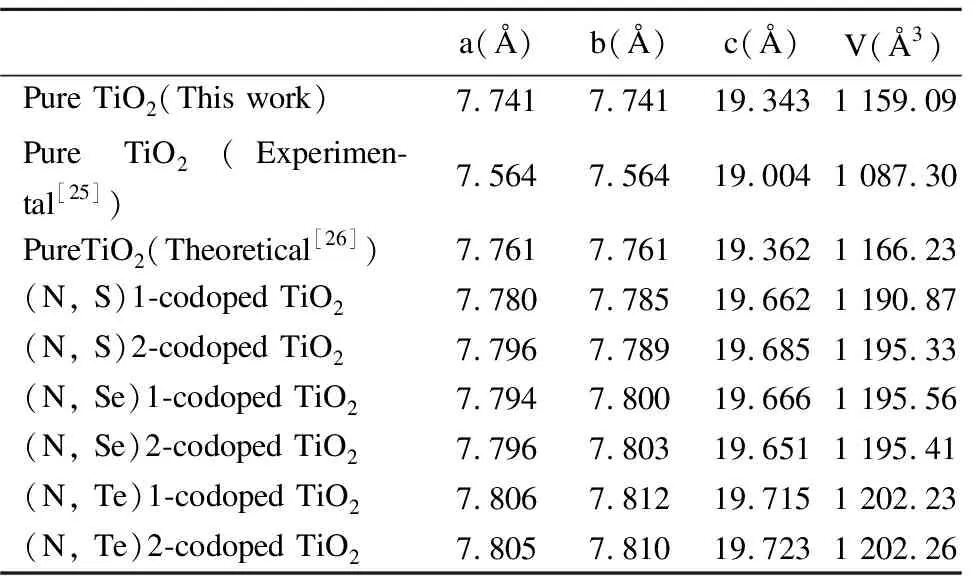
a(Å)b(Å)c(Å)V(Å3)Pure TiO2(This work)7.7417.74119.3431 159.09Pure TiO2(Experimen-tal[25])7.5647.56419.0041 087.30PureTiO2(Theoretical[26])7.7617.76119.3621 166.23(N, S)1-codoped TiO27.7807.78519.6621 190.87(N, S)2-codoped TiO27.7967.78919.6851 195.33(N, Se)1-codoped TiO27.7947.80019.6661 195.56(N, Se)2-codoped TiO27.7967.80319.6511 195.41(N, Te)1-codoped TiO27.8067.81219.7151 202.23(N, Te)2-codoped TiO27.8057.81019.7231 202.26

As seen from Table 1, for mono-doped anatase TiO2, the lattice parameters are almost unchanged.Compared with the volume of pure anatase TiO2(1 159.09 Å3), the volumes of mono-doped anatase TiO2are increasing, and the same cases appear in the codoped anatase TiO2.It is obvious that the volumes of codoped TiO2for replacing O and Ti have different large lattice expansions.By means of calculated data, it is noticed that the supercell has larger lattice expansions due to its larger atomic radius of Se (Se, 1.60 Å; Ti, 1.48 Å) and Te (Te, 1.70 Å; Ti, 1.48 Å), v.s smaller atomic radius of N (0.80 Å), S (1.12 Å) and O (0.60 Å).

2.2 Substitution energies

To compare the relative stability of these dopant combinations in anatase TiO2, substitution energy (Esub) of substitutionally doped systems (for either O or Ti) are estimated by

Esub=E(doped)-E(pure)-μN-μX(X=S,Se,Te)+μO+μTi.

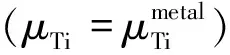
As for the so-called substitution energy, it is the energy difference of the system after and before the replacement.The substitution energy indicates that the dopant combinations tend to incorporate into supercell and integrate with each other when both of them are doped in anatase TiO2.The calculated results are summarized in Table 3.

Table3SubstitutionEnergyE(sub)(eV)forN-,S-,Se-,Te-doped, (N,S)-, (N,Se)-, (N,Te)-codopedanataseTiO2underTi-richandO-richconditions

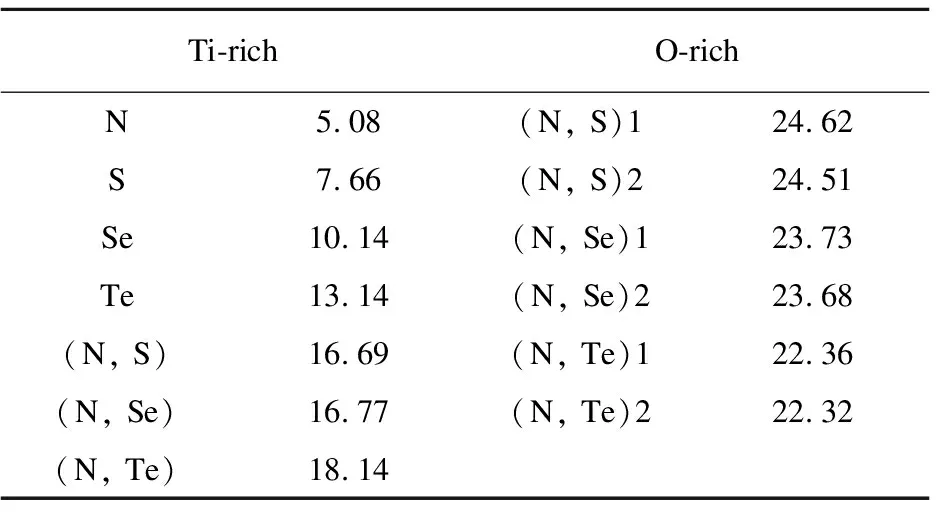
Ti-richO-richN5.08(N, S)124.62S7.66(N, S)224.51Se10.14(N, Se)123.73Te13.14(N, Se)223.68(N, S)16.69(N, Te)122.36(N, Se)16.77(N, Te)222.32(N, Te)18.14

As listed in Table 3, the substitution energies for N- or/and X(X=S, Se, Te)-doped anatase TiO2are 5.08, 7.66, 10.14, 13.14, 16.69, 16.77, 18.14 eV under Ti-rich grown condition and 24.62, 24.51, 23.73, 23.68, 22.36 and 22.32 eV under O-rich grown condition, respectively.These suggest that (1) N-doped is easy to incorporate into the anatase TiO2under Ti-rich grown condition; (2) With respect to the chalcogen elements substituting O site doped anatase TiO2, S is easy, but Te is hard.The same case is to be in the codoped systems; (3) Both N and X(X=S, Se, Te) at the substitutional sites are energetically and preferentially favorable under Ti-rich condition; (4) Under O-rich condition, the incorporation of X(X=S, Se, Te) are gradually decreased, but the case is opposite under Ti-rich condition; (5) The incorporation of X(X=S, Se, Te) can not promote the incorporation of N into bulk TiO2under both O- and Ti-rich grown conditions.The (N,Te)-codoped possesses the lowest substitution energy of 22.3 eV among the codoped systems under O-rich grown condition.At the same time, O-rich grown conditions are closest to the experimental environment in conjunction with the sol-gel method for the synthesis of titania.Hence, we will select this configuration to discuss its electronic structure with N- and X(X=S,Se,Te)-codoped compared with N or X(X=S,Se,Te) monodoping.N- and X(X=S,Se,Te)-codoped under Ti-rich condition has the substitutional energy, which is lower than that under O-rich condition.It is a large difference in the substitution energies obtained by means of DFT+U.The different substitution energies of dopants may be mainly caused by atomic radius.

2.3 Electronic structure

The key role to determine the photocatalytic efficiency of anatase TiO2is electronic structure.To understand the origin of band-gap narrowing, two cases about density of states (DOS) and partial DOS (PDOS) are discussed, as plotted in Figs.2 and 3.For comparison, DOS and PDOS of pure anatase TiO2are also shown in figures, with up-spin DOS above the Fermi level and down-spin DOS below the Fermi level.To modify the band structure of TiO2mono-doping and codoping, the compositions need to be investigated firstly.According to the PDOS of pure TiO2, it can be seen that the valance band edge of TiO2is mainly composed of O 2p states while the conduction band is dominated by Ti 3d states.

Fig.2 Calculated DOS and PDOS of pure anatase, N-, S-, Se- and Te-doped, (N, S)-, (N, Se)- and (N, Te)-codoped anatase TiO2 for substituting N with X(X=S, Se, Te) for O

For N-doped TiO2, substitution of N at O site, the electronic structures of N and O are 2s22p3and 2s22p4because N has one electron less than O with respect to p orbital character.In the PDOS of N-doped TiO2, N 2p orbit is mainly located at the top of valance band maximum (VBM) and some states exist in the conduction band.As shown in the DOS between pure TiO2and N-doped TiO2, from the VBM to the bottom of conduction band (CBM), there is hardly any change in N-doepd TiO2.In the case of that, N-doped TiO2is responsible for the photocatalytic activation in the visible-light irradiation.For S-doped TiO2, there are S 3p states localizing slightly above the upper edge of the valence band compared with undoped TiO2.Excitations from the impurity state of S 3p orbit to the conduction band may be responsible for the red shift of the absorption edge observed in S-doped TiO2[8].The width of band gap between VBM and CBM is narrower than that of pure TiO2and N-doped TiO2, which makes the band gap shift to the valance band.For (N, S)-codoped, S 3p orbital is strongly hybridized with N 2p orbit in the valance band.The impurity energy levels at the Fermi level sufficiently overlap with N 2p states located at the VBM of anatase TiO2.

For Se- and Te-doped and (N, Se)-, (N, Te)-codoped TiO2, it is significant from the PDOS that some impurity states below the Fermi level contain N 2p-Se 4p and N 2p-Te 5p states.The partial Se 4p and Te 5p states are split below the VBM and located at the edge of the conduction band.Incorporations of Se and Te into N-doped anatase TiO2make N 2p orbital character changed, which is fully occupied by N 2p-Se 4p and N 2p-Te 5p states above the VBM.The Se 4p and Te 5p orbital states are maximally dominated in the valance band edge, which makes Se 4p and Te 5p orbital energies vis-à-vis N 2p orbital energy be related to the more delocalized characters of 2p, 4p and 5p states.Therefore, incorporations of N and X(X=S,Se,Te) can modify the CBM and VBM because of their different p orbital energies with respect to N 2p, S 3p, Se 4p and Te 5p orbital states.

Substituting N for O and X(X=S, Se, Te) for Ti, the DOS and PDOS are plotted in Fig.3.

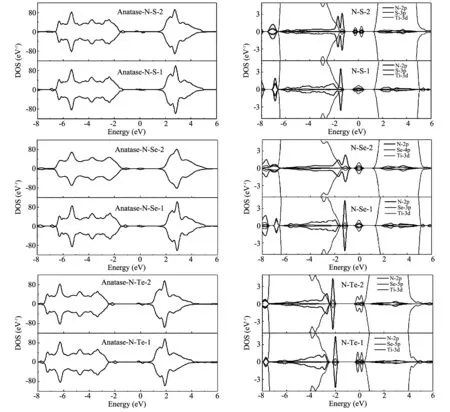
Fig.3 Calculated DOS and PDOS of pure anatase, N-, S-, Se- and Te-doped, (N, S)-, (N, Se)- and (N, Te)-codoped anatase TiO2 for substituting X(X=S, Se, Te) for Ti and N for O

For (N, S)-codoped TiO2, it is found that N 2p states are located above the VBM as well as mixing well with S 3p states.Ti 3d level is dominated by the host CBM while leaving N 2p and S 3p states residing deep in the conduction band.For (N, Se)-codoped case, the conduction band stems mostly from Ti 3d orbital but not from N 2p and Se 4p states.For (N, Te)-codoped, the width of CBM tail is larger than that of (N, S)-, (N, Se)-codoped case.With respect to pure TiO2, the CBM also originates from Ti 3d orbit, whereas S 3p, Se 4p and Te 5p orbits lie in the energy region.For (N, S)2-codoped TiO2, Ti 3d-N 2p-S 3p orbit is split into two parts.In this case, (N, Te)-codoped appears.It is possible that introduction of chalcogen elements into N-doped anatase TiO2leads to large lattice expansion by the large atomic radius.It is evidently found that Ti 3d level is located at the forbidden gap because the strong lattice expansion causes S 3p (Se 4p or Te 5p )-N 2p-Ti 3d hybridized states more significantly, which induces these states to reside in the middle of the gap region.Therefore, it is expected that these states are responsible for large gap narrowing and the hybridization effects may enhance the photocatalytic performance in the visible region.

To investigate the electrons transfer between N and X(X=S, Se, Te), a Bader[27,28]analysis of the charge density is performed.The average Bader charges are calculated for N and X(X=S, Se, Te) with respect to substituting N with X(X=S,Se,Te) for O, as plotted in Table 4.

Table4AverageBaderchargesondopantatomsandtheiradjacentatomsinN-,S-,Se-,Te-dopedand(N,S)-, (N,Se)-and(N,Te)-codopedanataseTiO2forsubstitutingNwithX(X=S,Se,Te)forO

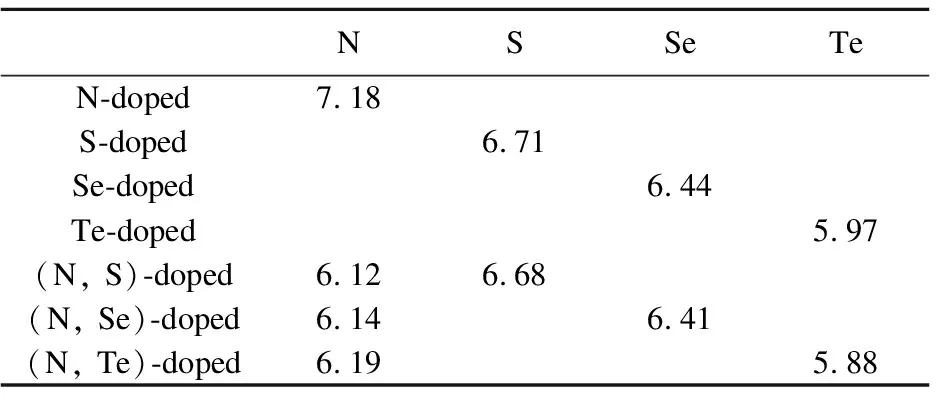
NSSeTeN-doped7.18S-doped6.71Se-doped6.44Te-doped5.97(N, S)-doped6.126.68(N, Se)-doped6.146.41(N, Te)-doped6.195.88

The obtained valance electron numbers for N- or X(X=S, Se, Te)- doped anatase TiO2are 7.18, 6.71, 6.44, 5.97, respectively.For N and X(X=S, Se, Te)-codoped anatase TiO2, the electron numbers are 6.12 and 6.68 for (N, S)-codoped, 6.14 and 6.41 for (N, Se)-codoped, 6.19 and 5.88 for (N, Te)-codoped, respectively.It is concluded that there are some changes in the codoped systems.Compared with mono-doped systems, the electron numbers of N are increasing gradually.In (N, S)- and (N, Se)-codoped TiO2, there are 0.56 and 0.27 electrons from S and Se to N, respectively.However, in (N, Te)-codoped, there are 0.31 electrons from N to Te.

For replacements of Ti and O with X(X=S, Se, Te) and N, the calculated results are summarized in the Table 5.The obtained valance electron numbers are 6.06 and 4.34 for (N, S)1, 6.05 and 4.30 for (N, S)2, 6.20 and 3.86 for (N, Se)1, 6.19 and 3.88 for (N, Se)2, 6.40 and 3.06 for (N, Te)1, 6.35 and 3.12 for (N, Te)2, respectively.According to the results, it is obviously found that there are about 1.25, 1.28, 1.30, 1.56, 1.13 and 2.02 electrons transfer from the chalcogen elements to N in the (N, S)-, (N, Se)-, (N, Te)-codoped anatase TiO2.

Table5AverageBaderchargesondopantatomsandtheiradjacentatomsinN,S,Se,Tedopedand(N,S)-, (N,Se)-and(N,Te)-codopedanataseTiO2forsubstitutingX(X=S,Se,Te)forTiandNforO

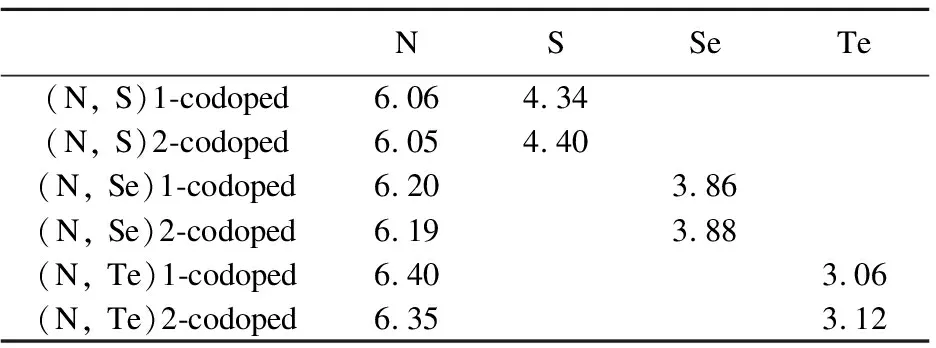
NSSeTe(N, S)1-codoped6.064.34(N, S)2-codoped6.054.40(N, Se)1-codoped6.203.86(N, Se)2-codoped6.193.88(N, Te)1-codoped6.403.06(N, Te)2-codoped6.353.12

3 Conclusion

The impact of N- and X(X=S, Se, Te)- codoped on the electronic properties of anatase TiO2has been systematically investigated using DFT method.By means of the optimized geometries, it is displayed that the lattice parameters become large expansions because of large atomic radius.According to substitution energies, it is indicated that incorporation of X(X=S, Se, Te) into N-doped bulk TiO2can not promote N synergistic effects for substituting Ti, whereas it is better for substituting O.The PDOS of substitutions of O makes N 2p states be strongly hybridized with impurity states S 3p, Se 4p, Te 5p states.Substituting X(X=S, Se, Te) for Ti atoms, Ti 3d level almost is dominated by the conduction band and forms S 3p (Se 4p or Te 5p )-N 2p-Ti 3d hybrid states.Finally, the Bader analysis demonstrates that the electrons transfer is from N to X(X=S, Se, Te) for chalcogen elements substituting O, however, the substitution of Ti is opposite.Therefore, it is indicated that elemental doping makes the excellent explanation of photocatalytic efficiency in the N- or/and X(X=S, Se, Te)- doped anatase TiO2.

[1] Linsebiger A L, Lu G Q, Yates J T.Photocatalysis on TiO2surfaces: principles, mechanisms, and selected results.Chemical Review, 1995, 95(3): 735-758.

[2] Fujishima A, Honda K.Photolysis-decomposition of water at the surface of an irradiated semiconductor.Nature, 1972, 238(5385): 37-38.

[3] Choi W, Termin A, Hoffmann M R.The role of metal ion dopants in quantum-sized TiO2: correlation between photoreactivity and charge carrier recombination dynamics.Journal of Physical Chemistry, 1994, 98(51): 13669-13679.

[4] Yamashita Y, Ichiashi M, Taeuchi S, et al.Characterization of metal ion-implanted titanium oxide photocatalysts operating under visible light irradiation.Journal of Synchrotron Radiation, 1999, 6(3): 451-452.

[5] WANG Yan-qin, CHENG Hu-min, ZHANG Li, et al.The preparation, characterization, photoelectrochemical and photocatalytic properties of lanthanide metal-ion-doped TiO2nanoparticles.Journal of Molecular Catalysis A-Chemical, 2000, 151(1/2): 205-216.

[6] Long R, English N J.Synergistic effects of Bi/S codoping on visible light-activated anatase TiO2photocatalysts from first principles.Journal of Physical Chemistry, 2009, 113(19): 8373-8377.

[7] Asahi R, Morikawa T, Ohwaki T, et al.Visible-light photocatalysis in nitrogen-doped titanium oxides.Science, 2001, 293(5528): 269-271.

[8] Umebayashi T, Yamaki Y, Itoh H, et al.Band gap narrowing of titanium dioxide by sulfur doping.Applied Physics Letters, 2002, 81(3): 454-456.

[9] CHEN Dai-mei, YANG Dong, WANG Qun, et al.Effects of boron doping on photocatalytic activity and microstructure of titanium dioxide nanoparticles.Industrial and Engineering Chemistry Research, 2006, 45(12): 4110-4116.

[10] Lindgren T, Mwabora J M, Avendano E, et al.Photoelectrochemical and optical properties of nitrogen doped titanium dioxide films prepared by reactive DC magnetron sputtering.Journal of Physical Chemistry B, 2003, 107(24): 5709-5716.

[11] Irie H, Watanabe Y, Hashimoto K.Nitrogen-concentration dependence on photocatalytic activity of TiO2-x N x powders.Journal of Physical Chemistry B, 2003, 107(23): 5483-5486.

[12] Jenks W S, Howk R S, Rockafellow E M, et al.Selenium-modified TiO2and its impact on photocatalysis.Langmuir, 2010, 26(24): 19052-19059.

[13] Curkan Y Y, Kasapbasi E, Cinar Z.Enhanced solar photocatalytic activity of TiO2by selenium (IV) ion-doping- Characterization and DFT modeling of the surface.Chemical Engineering Journal, 2013, 214(1): 34.

[14] GAO Hong-tao, LIU Yuan-yuan, DING Cui-hong, et al.Synthesis, characterization, and theoretical study of N, S-codoped nano-TiO2with photocatalytic activities.International Journal of Minerals Metallurgy and Materials, 2011, 18(5): 606-615.

[15] Behpour M, Atouf V.Study of the photocatalytic activity of nanocrystalline S, N-codoped TiO2thin films and powders under visible and sun light irradiation.Applied Surface Science, 2012, 258(17): 6595-6601.

[16] Kresse G, Hafner J.Ab initio molecular dynamics for liquid metals.Physical Review B, 1993, 47(1): 558-561.

[17] Kresse G, Furthmuller J.Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set.Physical Review B, 1996, 54(16): 11169-11186.

[18] Perdew J P, Burk K, Ernzerhof M.Generalized gradient approximation made simple.Physical Review Letters, 1996, 77(18): 3865-3868.

[19] Perdew J P, WANG Yue.Accurate and simple analytic representation of the electron-gas correlation energy.Physical of Review B, 1992, 45(23): 13244-13249.

[20] Davidson E R.Methods in computational molecular physics.Edited by Diercksen G H F, Wilson S D.Reidel Publishing Company, Dordrecht, Holland, 1982.

[21] Wilson S.NATO advanced study institute, series C.Plenum, Newyork, 1983, 113: 95-114.

[22] Monkhorst H J, Pack J D.Special points for Brillouin-zone integrations.Physical of Review B, 1976, 13(12): 5188-5192.

[23] Dudarev S L, Botton C A, Savarsov S Y, et al.Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study.Physical of Review B, 1998, 57(3): 1505-1509.

[24] Loschen C, Carrasco J, Neyman K, et al.First-principles LDA+U and GGA+U study of cerium oxides: dependence on the effective U parameter.Physical of Review B, 2007, 75(3): 035115-035123.

[25] Burdett J K, Hughbandks T, Miller G J, et al.Structural-electronic relationships in inorganic solids: powder neutron diffraction studies of the rutile and anatase polymorphs of titanium dioxide at 15 and 295 K.Journal of the American Chemical Society, 1987, 109(12): 3639-3646.

[26] Kamisaka H, Suenaga T, Nakamura H, et al.DFT-based theoretical calculations of Nb-and W-doped anatase TiO2: complex formation between W dopants and oxygen vacancies.Jourcal of Physical Chemistry C, 2010, 114(29): 12777-12783.

[27] Henkelman G, Arnaldsson A, Jónsson H.A fast and robust algorithm for Bader decomposition of charge density.Computational Materials Science, 2006, 36(3): 354-360.

[28] Sanville E, Kenny S D, Smith R, et al.Improved grid-based algorithm for Bader charge allocation.Journal of Computational Chemistry, 2007, 28(5): 899-908.