QIM digital watermarking based on LDPC code and message passing under scaling attacks

CUI Xin, YAN Bin, JIA Xia, WANG Ya-fei

(College of Information and Electrical Engineering, Shandong University of Science and Technology, Qingdao 266590, China)

The advent of Internet and other public information sharing networks has given rise to a multitude of applications in which data hiding plays a very important role.In particular, simple desynchronization operation can have a catastrophic impact on performance of the decoder, usually measured via the probability of correctly decoded hidden da-ta[1,2].In Ref.[3], a repetition code-aided quantization index modulation (QIM) watermarking algorithm, factor graph (FG) repetition code, is proposed.However, the transmission rate is low.Motivated by the iterative decoding theory, a low density parity check (LDPC) code-aided QIM watermarking algorithm, FG-LDPC, is proposed in this paper, which uses message passing in watermark decoding stage.The amplitude scaling parameters can be estimated based on LDPC code decoding and message passing on Forney style factor graph (FFG).Meanwhile, the newly estimated parameter estimation can be used to improve the performance of decoder in the next decoding iteration.Thus, it is an effective method against amplitude scaling attacks.

1 System model

The watermarking system model proposed in this paper is illustrated in Fig.1.

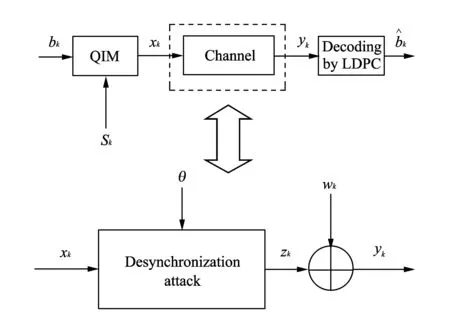
Fig.1 Model of watermarking and desynchronization attacks

2 Factor graph model and message passing algorithm

In general, an FFG consists of nodes, edges, and half edges which are connected only to one node.An edge is defined as a variable and a node is defined as a function of several variables[4,5].In this paper, three nodes are applied to the watermarking system model, as shown in Table 1.

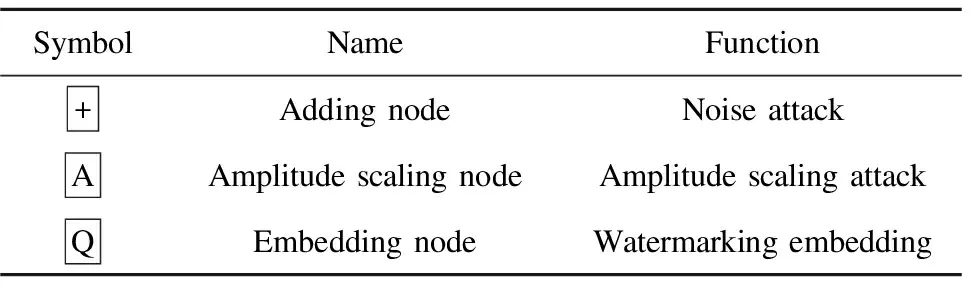
Table 1 Three FFG nodes in system model

According to the notation in Table 1 and using the basic sum-product rule, each model of FFG nodes is established and its corresponding message passing updating algorithms are designed[6].The results are shown in Tables 2, 3 and 4.

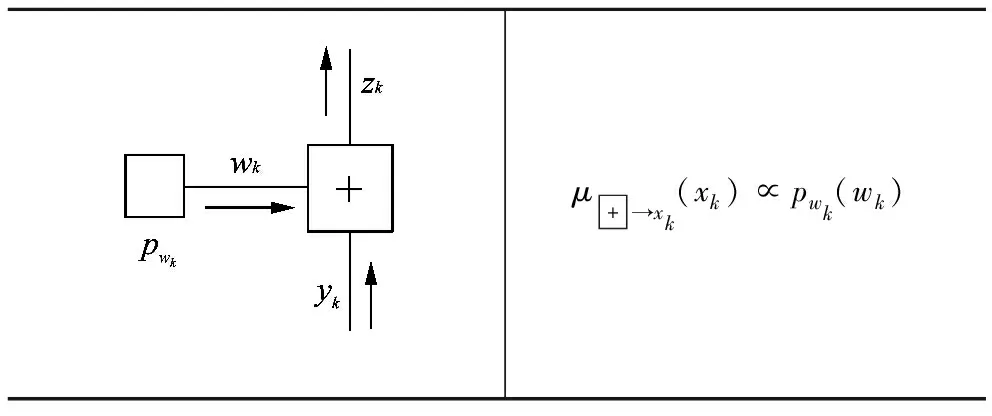
Table 2 Adding node model and message updating rule

Table3Amplitudescalingnodemodelandmessageupdatingrule

μA→xk(xk)∝μθk-1→A(θk-1)·μθk→A(θk)·∑xk∈Λ0∪Λ1μzk→A(θkxk)μA→θk(θk)∝μθk-1→A(θk-1)·∑xk∈Λ0∪Λ1μxk→A(xk)·μzk→A(xkθk)

whereμ→(·) is the message from original node to target node.The symbolpwk(·) andpSk(·) are denoted as the PDF of AWGN and that of host sequence, respectively.The symbolΛ0andΛ1are denoted as the quantification of lattice 0 and that of 1, respectively.The symbolθkdenotes the amplitude scaling parameter.The symbolQbk(·) is used to denote the quantizer of QIM[7,8].

Table 4 Embedding node model and message updating rule

In addition to local message passing rules, a global message passing schedule must be specified.Here we use a natural message passing schedule: The message is updated from the channel output data to the codewords.

Step 1: Update the message in the adding node;

Step 2: Update the message in the embedding node upward;

Step 3: Update the message in the embedding node downward;

Step 4: Update the message in the amplitude scaling node.Using “Step 1” and “Step 3” to compute amplitude scaling right message which contains N branches.Then the original amplitude scaling right message can be updated by it.

Step 5: Circle the whole message passing algorithm until the decoded codeword does not change over iterations.

3 Simulation results

To test the performance of the FG-LDPC algorithm proposed in this paper, simulation is conducted.The watermarking signal is encoded by regular (3, 6) LDPC code.The code rate is 1/2 and code length is 4 000.In the simulation, the host-to-watermark (HWR) is 25 dB and the host signal standard deviation is 50 dB.Fig.2 shows the simulation results of FG-LDPC algorithm.Here, the symbol WNR is denoted as the watermark-to-noise ratio.

It can be seen from Fig.2, FG-LDPC algorithm is closer to Shannon limit than FG-repetition code algorithm[9,10].Compared with FG-repetition code algorithm, FG-LDPC algorithm has a good performance when the system is attacked by AWGN.

In Fig.3, amplitude scaling parameters conform to the uniform distribution in the region of [0, 2].We test the accuracy of amplitude scaling parameter estimation when FG-LDPC algorithm is attacked by amplitude scaling and AWGN.The results show that the algorithm can estimate amplitude scaling parameter with low WNR.

Fig.2 Performance of FG-LDPC algorithm

Fig.3 Accuracy of amplitude scaling parameter estimation with FG-LDPC algorithm (WNR: 3 dB)

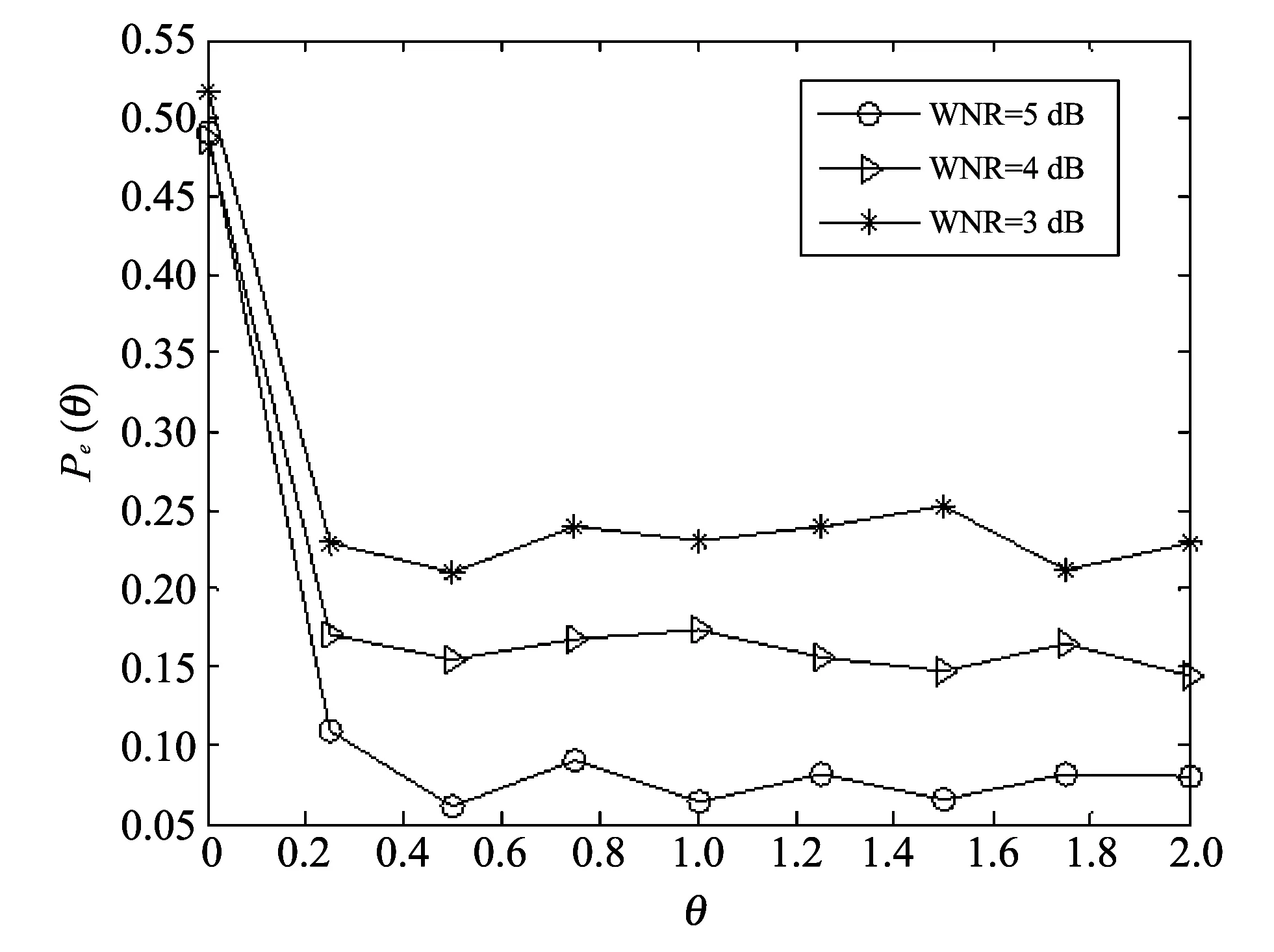
Fig.4 Stability of amplitude scaling parameter estimation (host: Gaussion)

In Fig.4, the stability of amplitude scaling parameter estimation is tested.In different WNRs, the volatility of the curve is so small that it can be concluded that the algorithm can reach stability when estimating the scaling parameters.Meanwhile, the better performance of parameter estimation can be achieved with the increase of WNR.

In Fig.5, we test the performance of FG-LDPC algorithm when the algorithm is attacked by amplitude scaling.Compared with the algorithm, the simulation results show that the algorithm can obtain similar performance without desynchronization.Compared with the situation that is no code aided or only 10-pilot aided, FG-LDPC algorithm has better performance.

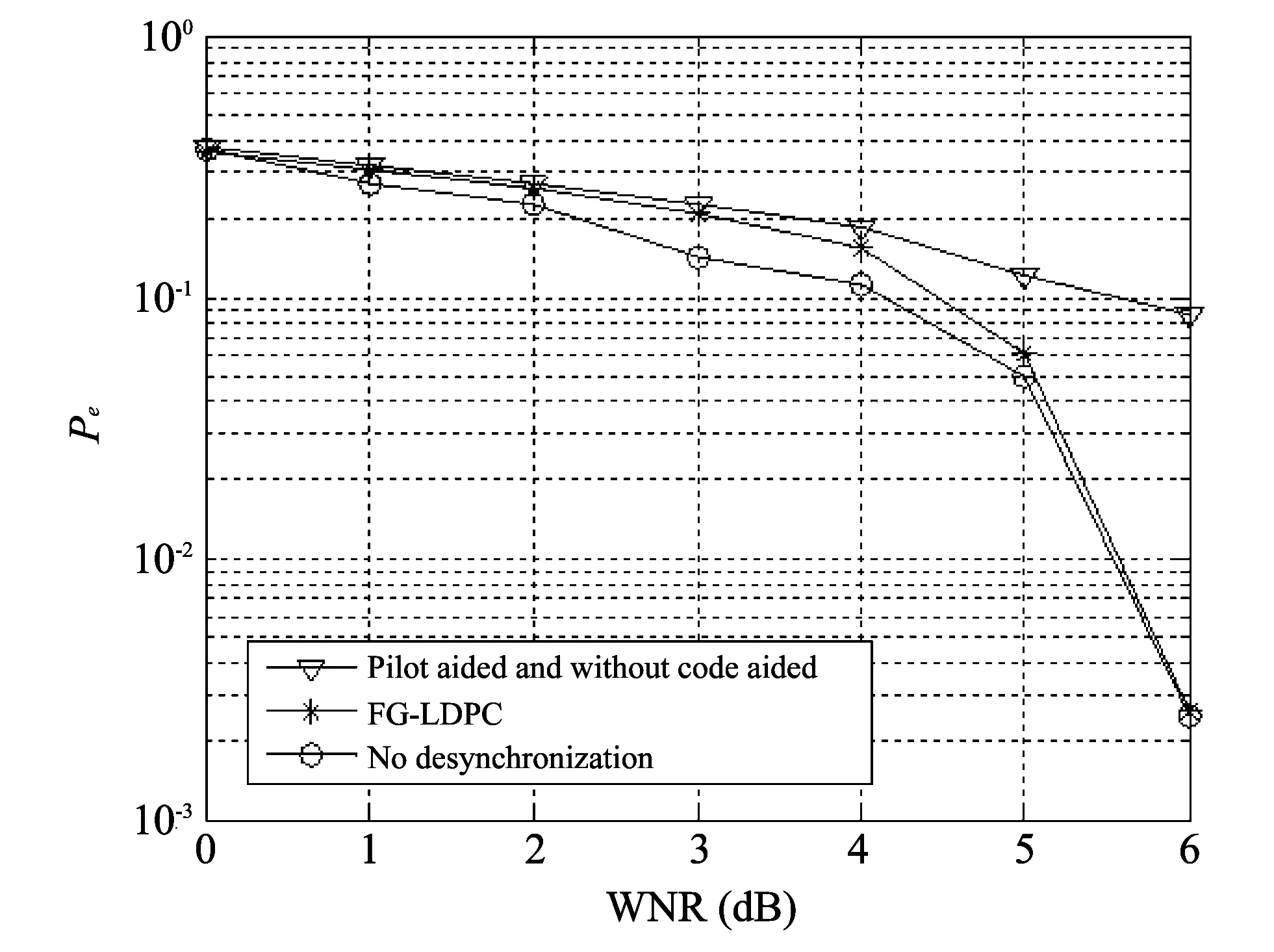
Fig.5 FG-LDPC algorithm with amplitude scaling

4 Conclusion

Using the framework of iterative estimation and decoding, LDPC coded QIM watermarking system is closer to dirty paper Shannon limit than repetition coded system.In addition, it is superior to pilot based system.

[1] Cox I J, Miller M L, Bloom J A.Digital watermarking.Beijing: Publishing House of Electronics Industry, 2002: 78-103.

[2] Moulin P, Briassouli A, Malvar H.Detection-theoretic analysis of desynchronization attacks in watermarking.In: Proceedings of the 14th International Conference on Digital Signal Processing, Santorini, Greece, 2002, 1: 77-84.

[3] Sadasive S, Moulin P.A message passing approach to combating desynchronization attacks.IEEE Transactions on Information Forensics Security, 2011, 6(6): 1-13.

[4] Loeliger H A.An introduction to factor graphs.IEEE Signal Processing Magazine, 2004, 21(1): 28-41.

[5] Loeliger H A, Dauwels J, HU Jun-li, et al.The factor graph approach to model-based signal processing.In: Proceedings of the IEEE, 2007, 95: 1295-1322.[doi:10.1109/JPROC.2007.896497]

[6] Dauwels J H G.On graphical models for communications and machine learning: algorithms, bounds, and analog implementation.Series in Signal and Information Processing, 2006, 17: 100-150.

[7] Chen B, Wornel G W.Preprocessed and post-processed quantization index modulation methods for digital watermarking.In: Proceedings of International Society for Optics and Photonics: Security and Watermarking of Multimedia Contents II, 2000, 3971: 48-59.

[8] Borne D V D, Kalker T, Willems F.Codes for writing on dirty paper.In: Proceedings of the 23rd Symposium on Information Theory, Benelux, 2002: 45-52.

[9] Perez-Gonzalez F, Hernandez J R, Balad F.Approaching the capacity limit in image watermarking: a perspective on coding techniques for data hiding applications.Signal Processing, 2011, 81: 1215-1238.

[10] Johnson S J.Iterative error correction.UK: Cambridge University Press, 2010: 34-279.