Dynamic compensation for sensors based on particle swarm optimization and realization on LabVIEW
ZHANG Xia, ZHANG Zhi-jie, CHEN Bao-li
(School of Information and Communication Engineering, North University of China, Taiyuan 030051, China)
For most of the sensors,there are such defects as dynamic response lag and static nonlinear distortion under the conditions of current technology.To establish a linear relationship between input signal and output signal, some methods are necessary, for example, intermediate compensation and correction.
With the popularity of computer technology, subsequent processing for output signal of sensor with software or a dynamic compensation filter has been widely used.Generally, the methods of designing a dynamic compensator include zero-pole assignment method and system identification method, etc.Especially, if using these methods, the structure of dynamic compensation filter must be constructed in advance.Furthermore, if the sensor is used in a high-order nonlinear system, the structure design of dynamic compensation filter is very complex.
In this paper, particle swarm optimization (PSO) algorithm is used for dynamic compensation for the sensor to overcome the shortcomings of the above methods.The test results show that the sensor after compensation obtains the required ideal dynamic characteristics.
1 Dynamic compensation principle based on particle swarm optimization (PSO) algorithm[1-4]
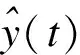

Fig.1 Principle of dynamic compensation for sensor
In order to avoid building dynamic model of the sensor, this paper directly designs dynamic compensation filter using the experimental data.The essence of this method is to transform dynamic compensation filter design into compensation filter parameters by means of the experimental data.The specific principle is described as follows.
The dynamic compensation for sensors can be described as a single variable differential equation in practical application,
y(t)(b0+b1z-1+…+bmz-m)+e(t),
(1)
wherez-1is delay operator,mandnare steps of the compensation filter ande(t) denotes output noise.To simplify the expression, Eq.(1) can be expressed as a vector form,
(2)
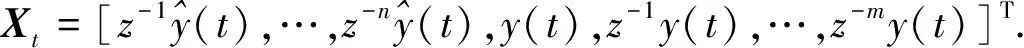
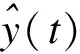
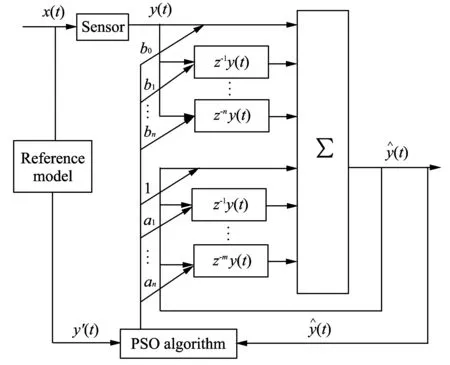
Fig.2 Principle of dynamic compensation of sensors based on PSO
2 PSO algorithm
2.1 Principle of PSO algorithm
PSO is a kind of excellent evolutionary algorithm, which has developed rapidly in recent years and become simpler and more efficient than genetic algorithm in coding and optimization strategy[5].The basic idea of PSO is to initialize a group of random particles, and then look for the optimal solution via iteration.In each iteration, the particles update their position by tracking two “extremums”: one is the optimal solution found by themselves, called individual extreumpbest; the other is the optimal solution found by the overall group at present, called the global extremumgbest.Then the speed and position are updated by
V=wV+c1r( )(pbest-p)+c2r( )(gbest-p),
(3)
p=p+V,
(4)
whereVdenotes the particle's speed;Pdenotes the particle's current position;pbestandgbestare individual extremum and global extremum, respectively;c1andc2are learning factors between 0-2;r( ) is the random function between (0,1);w(k) is weighting factor, which reduces linearly from the maximum weighting factorwmaxto the minimum weighting factorwminwith the iteration proceeding, as described by
(5)
In the initial stage of iteration,wselects a larger value to guarantee fast searching speed, and later it selects a smaller value to guarantee the convergence of the algorithm.Typical values are:wmax=0.9 andwmin=0.4.
In this paper, the fitness function using mean square error (MSE) is defined as
(6)
whereNis the sample size.
PSO algorithm has characteristics of less parameters, fast convergence and efficiency, so it has been widely used in the optimization process.The specific steps of calculating the dynamic compensation filter's coefficients are as follows.
1) Initialize the speed and position of each particle from the particle swarm within the given target area;
2) Set the parameters of PSO algorithm and calculate the fitness of the particles according to Eq.(6);
3) Update the particle's speed and position according to Eqs.(3) and (4) and calculate the fitness of each particle again;
4) Judge whether the particle's individual extremumpbestand the particle swarm's global extremumgbestare updated or not;
5) Repeat 4) and 5) until meeting the accuracy requirement or reaching the number of iterations;
6) Get outputgbestand the compensation coefficients.
2.2 Validation of PSO algorithm[6-8]
The algorithm is validated by the dynamic calibration experiment for the pressure sensor.In the experiment, the shock tube is used to generate a standard step pressure to press on the measured pressure sensor.Then the pressure sensor is calibrated and actual working performance is analyzed according to the output response of the pressure sensor.The curve 1 in Fig.3 is a piece of data starting from the first rising edge of the measured response curve of the pressure sensor obtained in the dynamic calibration experiment.
Creating a inverse model using PSO algorithm, it makes the sensor output equivalent to compensation filter input, and the sensor input equivalent to the compensator output.In Fig.3, curve 1 is the input of compensation system and the output of reference model is an ideal step signal.The 3-order compensation filter's coefficients can be got by using the above method.Curve 2 is the compensation result with the response-time of 10 μs and overshoot volume of 10%, which achieves the technical requirements.
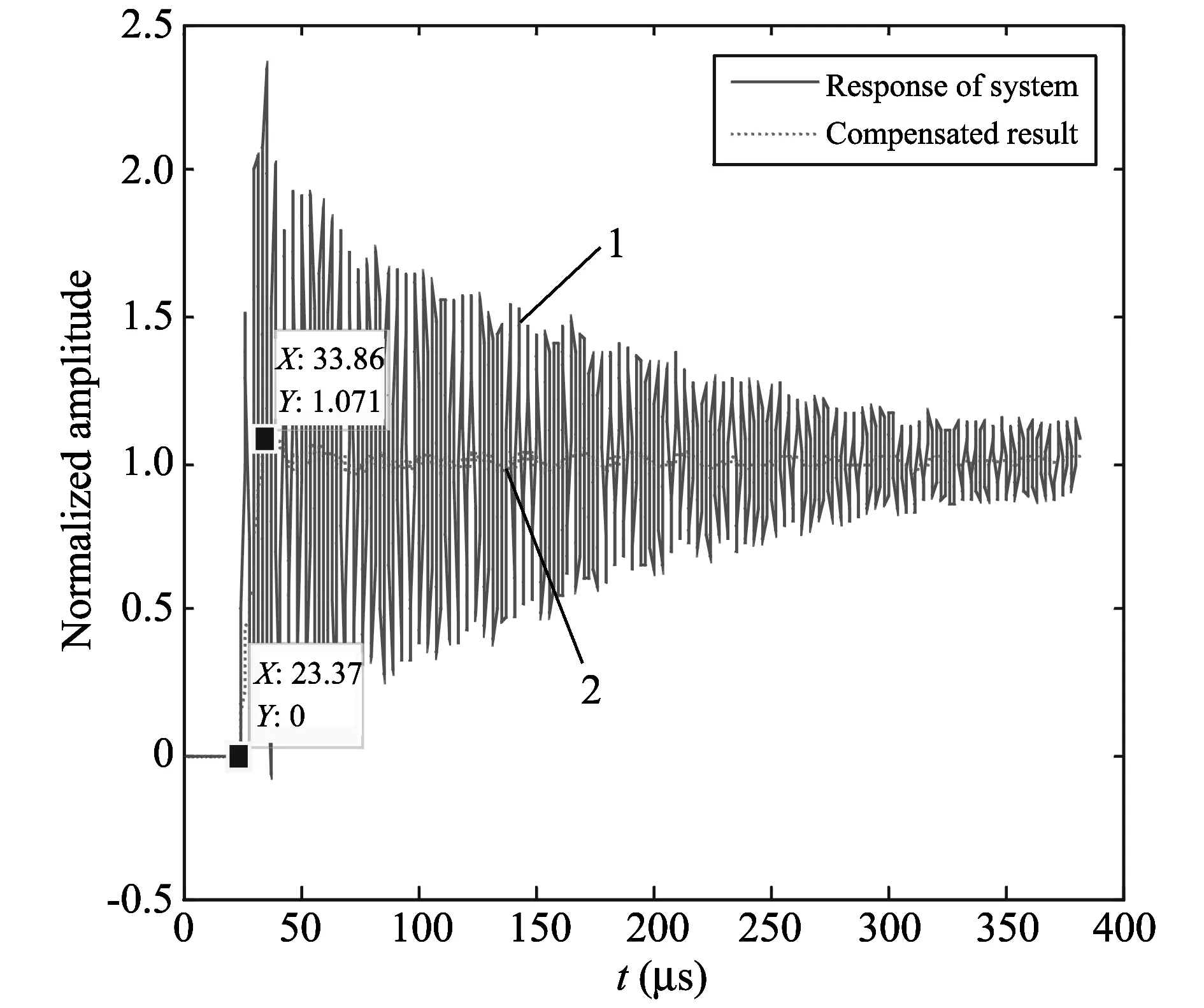
Fig.3 Compensation result
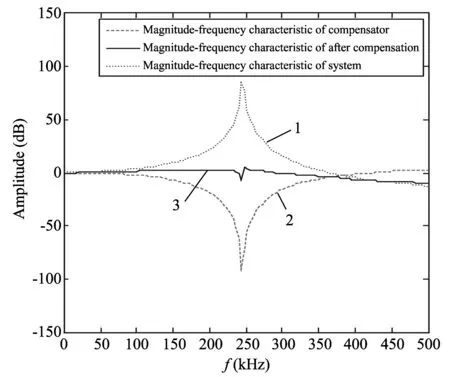
Fig.4 Contrast of amplitude frequency characteristics before and after compensation
In order to verify compensation effect, the amplitude frequency characteristics of the system before and after compensation are compared.Firstly, the sensor model is established using the above method, and then the amplitude frequency response is worked out, as shown in Fig.4.Curve 2 shows amplitude frequency characteristic of the dynamic com-pensation filter.Finally, the amplitude frequency response of the system after compensation is calculated, as curve 3 shows in Fig.4.It can be seen from Fig.4 that the amplitude frequency characteristic of the sensor has a a flat working band below 70 kHz, but a larger amplitude error near the resonance frequency (245 kHz).The working band is extended to 400 kHz by dynamic compensation filter.Therefore, PSO algorithm can extend the effective working band of sensors.
3 Realization on LabVIEW[9]
LabVIEW has extensive applications in the measurement and control fields owing to powerful features and lots of advantages, so it is of important practical significance to realize the dynamic compensation for sensor on the LabVIEW platform.In this paper, PSO algorithm on LabVIEW platform is implemented.The modeling process of PSO needs a large amount of calculation and complex programming.To improve the efficiency of programming, training model on Matlab platform is established, and the model and parameters are obtained.This method implements the mixed programming by invoking COM component generated by M-file to achieve dynamic compensation for sensors.The method is as follows.
1) Configurate COM component compiler.Input ‘mbuild-setup’ command and select the appropriate C/C++ compiler.Set the compiler according to hint step by step until the configuration is completed successfully.
2) Generate COM component.Firstly, create a new m-function which defines statements using the ‘Function’ keyword and design compensation using ‘filter’ function with the coefficients got by modeling.Secondly, create a new project by inputting ‘deploytool’ command, and add the created m-file.Finally, compile and package the engineering.The generated DLL file is COM component.
3) Register COM component.Start the_install.bat file to complete the component's register inside the computer.So other ActiveX client can invoke COM component.
4) Invoke COM component on LabVIEW.Program block diagram is shown in Fig.5.The implementation effect is shown in Fig.6.

Fig.5 Program block diagram on LabVIEW
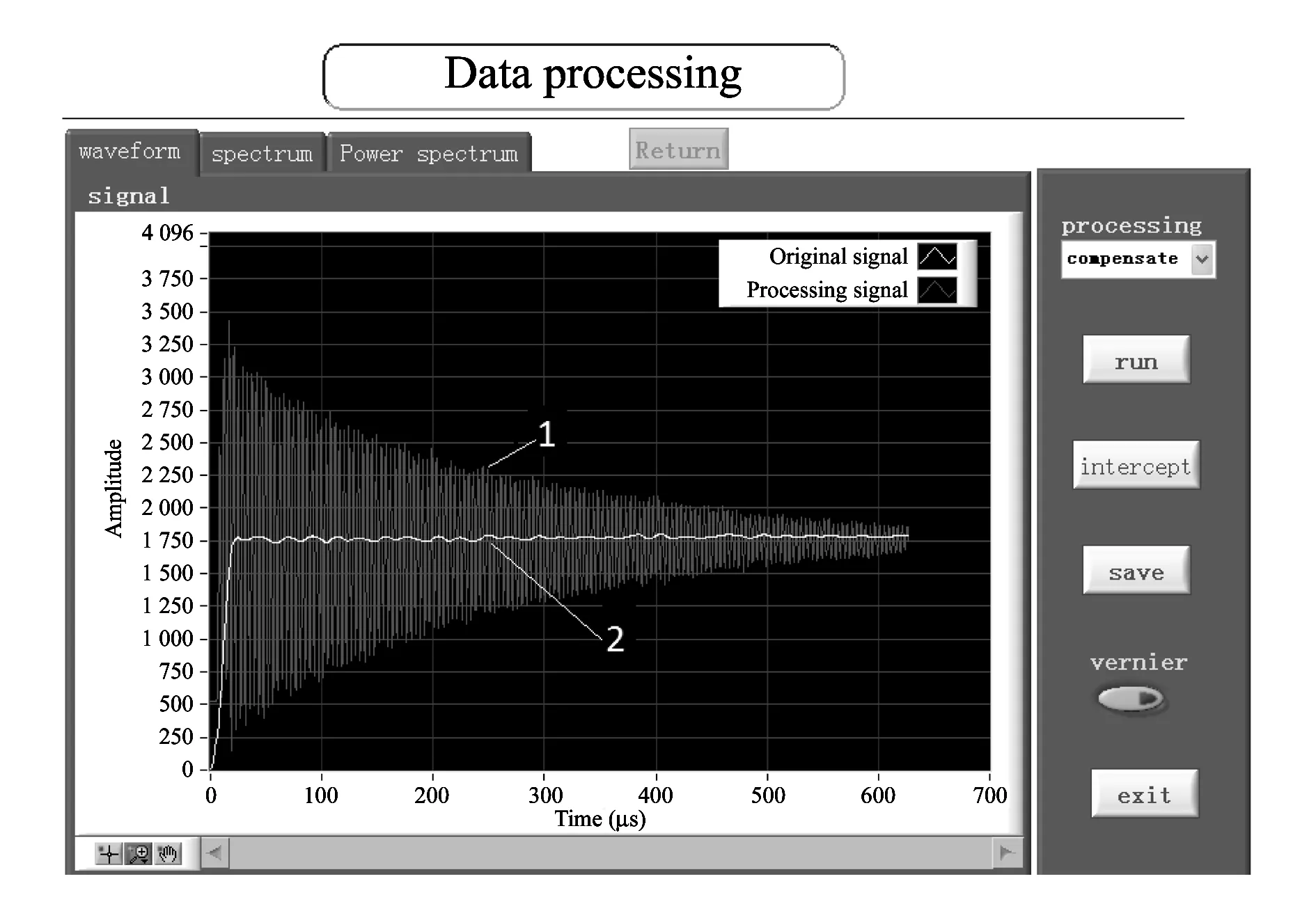
Fig.6 Results of dynamic compensation
4 Conclusion
For dynamic test, it is important to broaden the passband of sensors using dynamic compensation technology to reduce measuring error.The method based on PSO algorithm establishes an optimal dynamic compensation filter by optimizing the sensor's input and output through the calibration experiment.Without modeling process, there is not modeling error.In this paper, the feasibility of compensation filter is verified, and the experimental results show that the application of PSO algorithm in sensor's dynamic compensation is an effective method.
[1] WU Jian, ZHANG Zhi-jie, DONG Gang-gang, et al.
Real-time correction for sensor's dynamic error based on DSP.In: Proceedings of 2011 IEEE International Instrumentation and Measurement Technology Conference, Hangzhou, China, 2011: 633-639.
[2] ZHANG Yuan-yuan, XU Ke-jun, XU Yao-hua.Dynamic modeling approach based on improved PSO and FLANN for a sensor.Journal of Vibration and Shock, 2009, 28 (1): 1-7.
[3] TIAN Wen-jie, LIU Ji-cheng.A new optimization algorithm for dynamic compensation of sensors.In: Proceedings of the 2nd International Conference on Computer Modeling and Simulation, 2010, 2: 38-41.
[4] WU De-hui, HUANG Song-ling, XIN Jun-jun.Dynamic compensation for an infrared thermometer sensor using LSSVR based FLANN.Measurement Science and Technology, 2008, 19(10): 105202-105208.[doi:10.1088/0957-0233/19/10/105202]
[5] GAO Zhen-bin, ZENG Xiang-ye, WANG Jing-yi, et al.FPGA implementation of adaptive IIR filters with particle swarm optimization algorithm.In: Proceedings of the 11th Singapore International Conference on Communication Systems (ICCS 2008), Guangzhou, China, 2008: 1364-1367.[doi: 10.1109/ICCS, 2008.4737406]
[6] CHEN Sheng, Luk B L.Digital IIR filter design using particle swarm optimization.International Journal of Modelling Identification and Control, 2010, 9(4): 327-335.
[7] Ben Arfia F, Ben Messaoud M, Abid M.Nolinear adaptive filters based on particle swarm optimizer.Leonardo Journal of Sciences, 2009, 14: 244-251.
[8] ZHAO Zhong-kai, GAO Hong-yuan.FIR digital filters based on cultural particle swarm optimizer.In: Proceedings of 2009 International Workshop on Information Security and Application (IWISA 2009), Qingdao, China, 2009: 252-255.
[9] CHEN Xi-hui, ZHANG Yin-hong.LabVIEW8.20 programming from entry to the master.Beijing: Tsinghua University Press, 2007.
 Journal of Measurement Science and Instrumentation2014年1期
Journal of Measurement Science and Instrumentation2014年1期
- Journal of Measurement Science and Instrumentation的其它文章
- Error separation in CMM coordinate metrology
- Design and theoretical analysis of test system for propellants’ gas pressure in warhead
- A new probe for atmospheric electric field mill
- Experimental analysis of high temperature capacitance variance of MLCC
- Application of RLS adaptive filtering in signal de-noising
- QIM digital watermarking based on LDPC code and message passing under scaling attacks
