均值漂移优化的粒子滤波目标跟踪方法初

红霞，司金龙，宋起超，于浩洋，韩 晶，张 鹏，秦 杰

(黑龙江工程学院 电气与信息工程学院，黑龙江 哈尔滨 150050)

均值漂移优化的粒子滤波目标跟踪方法初

红霞，司金龙，宋起超，于浩洋，韩 晶，张 鹏，秦 杰

(黑龙江工程学院 电气与信息工程学院，黑龙江 哈尔滨 150050)

为了实现粒子集的有效传播，克服粒子滤波跟踪时的退化问题，提出尺度和方向自适应的均值移动优化粒子滤波目标跟踪算法。用改进的均值移动作为一种优化机制对粒子进行传播，使粒子能够有效分散和聚类，有效解决退化问题。最后将该方法应用到真实图像序列中，实验表明算法在性能和效率上有明显提高。

均值移动；粒子滤波；自适应；跟踪

粒子滤波是一种有发展前景而且被广泛采用的视觉跟踪方法。但在粒子的传播过程中，由于粒子的过度发散或集中都会导致退化现象的发生，因此，需要粒子集的有效传播来减少退化现象的发生。研究人员利用粒子滤波的开放跟踪框架体系，找到与它的结合点，即在这种框架下引入各种方法与跟踪技术实现粒子集的有效传播。

作为跟踪的主流方法之一，均值移动算法在目标跟踪中的最大优点是计算量很少，而且能实现对粒子的传播，很适用于实时跟踪系统。基于此，研究人员提出了将均值移动和粒子滤波算法相结合来解决此类问题，提高算法整体的实时性。几种混合粒子滤波器/均值移动跟踪方法已经被提出，Maggio等[1]在每次Condensation迭代中使用均值移动跟踪将粒子向评价函数的局部极大值处移动。算法显示了比凝聚算法和核均值移动更多的优势，但还有一些缺限。如果凝聚趋向于一个不正确的局部最大值，均值移动将加速这一过程。

通过对文献[2-5]中粒子滤波算法的深入分析还发现，算法重点在于能同时使粒子交替分散和聚类，提供某种程度的平衡，在减少粒子集的同时，避免粒子退化和采样贫瘠。本文使用尺度和方向自适应的均值移动算法(SOAMST)[6]聚类粒子集，最终完成粒子的有效传播，有效地处理了目标遮挡和尺寸变化情况下的跟踪问题。

1 系统状态模型

应用零阶自适应模型学习描述目标状态的变化。此模型在前k帧计算平均状态速度，即为

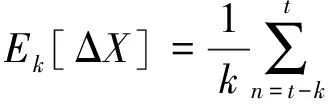
因此，状态转移模型定义为

Xt=Xt-1+Ctvt.

(1)

式中：Ct∝Ek[ΔX]，vt为零均值高斯白噪声。粒子集通过这个简单的常速模型传播。

2 系统颜色特征观测模型

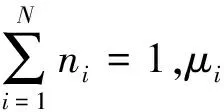
为了获得目标候选状态的颜色似然函数，需要将候选空间直方图和参考直方图相比较。将空间直方图看作加权高斯混合(每个空间直方图的子空间作为权值ni的高斯分布)N(μi,∑i)，Bhattacharyya系数推导为

(2)

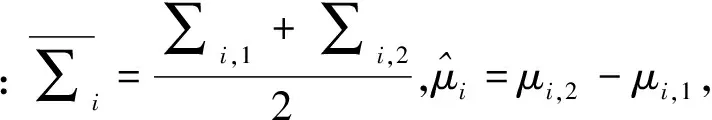
dc(hx,href)=(1-ρ)1/2.

(3)

假定平方距离是指数分布，则颜色似然模型为

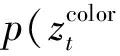
(4)

3 均值漂移优化的粒子滤波目标跟踪算法

图1给出均值移动优化粒子滤波目标跟踪算法的流程。下面将给出均值移动优化的粒子滤波目标跟踪算法实现步骤：

1)使用式(1)采样粒子。

2)用尺度和方向自适应变化的均值移动算法(SOAMST)[7]对粒子进行传播，即对每个粒子进行优化直到所有的粒子都到达一个稳定的位置。

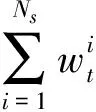
(5)

3)权值更新。根据系统观测模型中粒子的似然性确定权值。

(6)

4)模板更新。为了适应光照和遮挡等外部因素的影响，算法在跟踪过程中自适应对模板进行更新。假设当前模板为P，预测位置的直方图为Q，则当两者之间的Bhattachayya距离小于某个给定阈值T时，才对模板Q进行更新，否则认为外部点影响比较大，不进行更新。

图1 均值移动优化粒子滤波目标跟踪算法的流程

Qnew=(1-η)×Q+η×P，

式中：η为调整参数。

5)计算后验概率，得到目标状态，即

4 实验结果和分析

实验重点有两个方面的内容:一是粒子滤波和均值移动优化粒子滤波算法在目标跟踪中的效果对比。两种算法在背景单一且没有尺度变化和遮挡时的跟踪效果不容易区分，主要考查在目标有背景遮挡、尺度变化和有相似背景情况下算法的不同表现；二是讨论两种算法在跟踪同一目标算法执行时间的对比,实验中采用的特征提取方法及参数设置如下：

在目标区域RGB空间颜色直方图以N=N1N2N3=10×10×10个子空间计算，σc=5.5。目标状态X=(x,y,w,h)，其中(x,y)为目标的位置，(w,h)为目标区域的宽、高。

4.1 遮挡视频的实验结果及其分析

当视频中有运动遮挡物发生时，跟踪算法在跟踪精度上会急剧下降。为了验证所提出算法对各种复杂场景条件视频的跟踪精度的提高，首先用来源于http://www.cse.psu.edu/～rcollins/CSE598G的有严重遮挡情况下航拍的车辆运动视频进行了测试。所用视频中车辆在行驶过程中不时受到树木或树荫的大部分或几乎全部遮挡，树木的高矮和树荫的大小也在不断变化，有时只有车辆的极小部分区域在图像序列中显示。图像序列中每帧图像大小为640×480像素，共有450帧。

图2和图3给出了采用文献[3]中的粒子滤波器和本文改进方法跟踪关键帧的跟踪结果。从跟踪结果能够看出，所提出的算法对于这种严重遮挡的视频仍能精确定位目标，而文献[3]中的粒子滤波器则会发生较大偏差。尽管粒子滤波器可以通过使用较多粒子的随机分布来预测目标状态，但当遮挡发生时，只有很少的粒子能被分布在未被遮挡部分，这些粒子具有较大的权值，而遮挡部分的粒子权值则较小，因此，对目标状态的估计则主要由那些权值较大的粒子决定，此时粒子出现退化现象，最终造成跟踪的偏差，从图中还可以看出，遮挡发生时粒子滤波算法不能连续地跟踪目标，即在跟踪过程中当遮挡发生后，不能很好地定位目标，瞬间或间断帧内丢失目标。而应用均值移动算法对每一个粒子进行优化传播，使每一个粒子都能以自适应尺度和方向移动到邻域内的最大值点，更接近目标真实分布，实现连续定位，同时算法采用了自适应更新模板策略，遮挡结束后能恢复正确的跟踪，最终得到目标的准确位置，从而实现精确跟踪。结果表明，改进的算法在受到严重遮挡的影响下依然能稳定准确地跟踪到目标，保持了粒子滤波本身高鲁棒性和抗遮挡能力强的特点。

图2 退火粒子滤波跟踪结果

图3 本文改进粒子滤波跟踪结果

4.2 尺度变化视频的实验结果及其分析

采用来源于文献[8]的motinas_emilio_webcam_turning序列，从第1帧到110帧中被跟踪的头部有一个明显的尺度变化过程，目标从远离摄像机的位置向摄像机走来，逐渐变大。图4(a)采用文献[3]中的粒子滤波器的跟踪结果。其中：所采用的粒子数为500个，可以看出这时的粒子滤波器不能对目标位置进行很好地估计，当目标尺度变化时，预测的目标位置偏离了目标。分析其原因是由于目标状态向量包含4个变量，在采用退火粒子滤波方法进行目标状态估计时，每个粒子的状态在四维空间变换。如果想要得到对目标状态很好的估计，必须使用大量的粒子。本文即使将粒子数增加到500个，从图中也可以看出，这时目标的跟踪精度比少于500个粒子时会有所提高，如图4(a)第2幅图表明粒子能较好地近似目标状态。然而在其后的各帧中，尽管采用较多的粒子数目，仍产生了偏差和跟踪瞬间丢失现象。这是由退火粒子滤波器的跟踪原理决定的，目标不仅存在着位置的变化，而且存在尺度和方向的变化，使得目标状态搜索空间增大，很难通过采用大量粒子来估计目标状态。

图4(b)给出了采用本文方法的跟踪结果。与采用退火粒子滤波器的跟踪方法相比，本文提出的方法中，只使用100个粒子，由于均值移动算法对粒子滤波器的传播过程的优化作用，能够自适应地预测目标的大小和位置，使跟踪窗口能随着目标尺度的大小变化作出相应调整，缩小目标搜索区域。因此，仅需要较少的粒子来预测目标的大致区域，大大提高了算法的实时性。

图4 两种算法的跟踪比较

为了验证算法的执行效率，图5给出两种算法在跟踪实验中执行时间的对比。由图5可知，均值移动优化粒子滤波算法在实际跟踪中平均执行时间为15.456 5 ms。退火粒子滤波跟踪算法在粒子数为500个的条件下平均执行时间为84.564 0 ms，算法平均执行时间接近粒子滤波算法的1/5。可以看出，本文算法只需用100个粒子就能有好的跟踪效果，算法的实时性有很大提高。当尺度骤变时，退火粒子滤波器用来描述目标状态的粒子急剧增多或减少，这时候经动态模型传播后粒子的可变参数，如方向、速度、尺度等随之突变，因此，算法瞬时计算粒子分布的运算量增加，图5中时间曲线可以看到出现了几处较高的峰值。而改进的算法由于在动态模型传播后使用均值移动算法对每个粒子做聚集作用，有效抑制由于尺度骤变带来的计算量急剧增大的影响。因此，图5中算法运算时间几乎没有出现较高的峰值，而且稳定性更好。

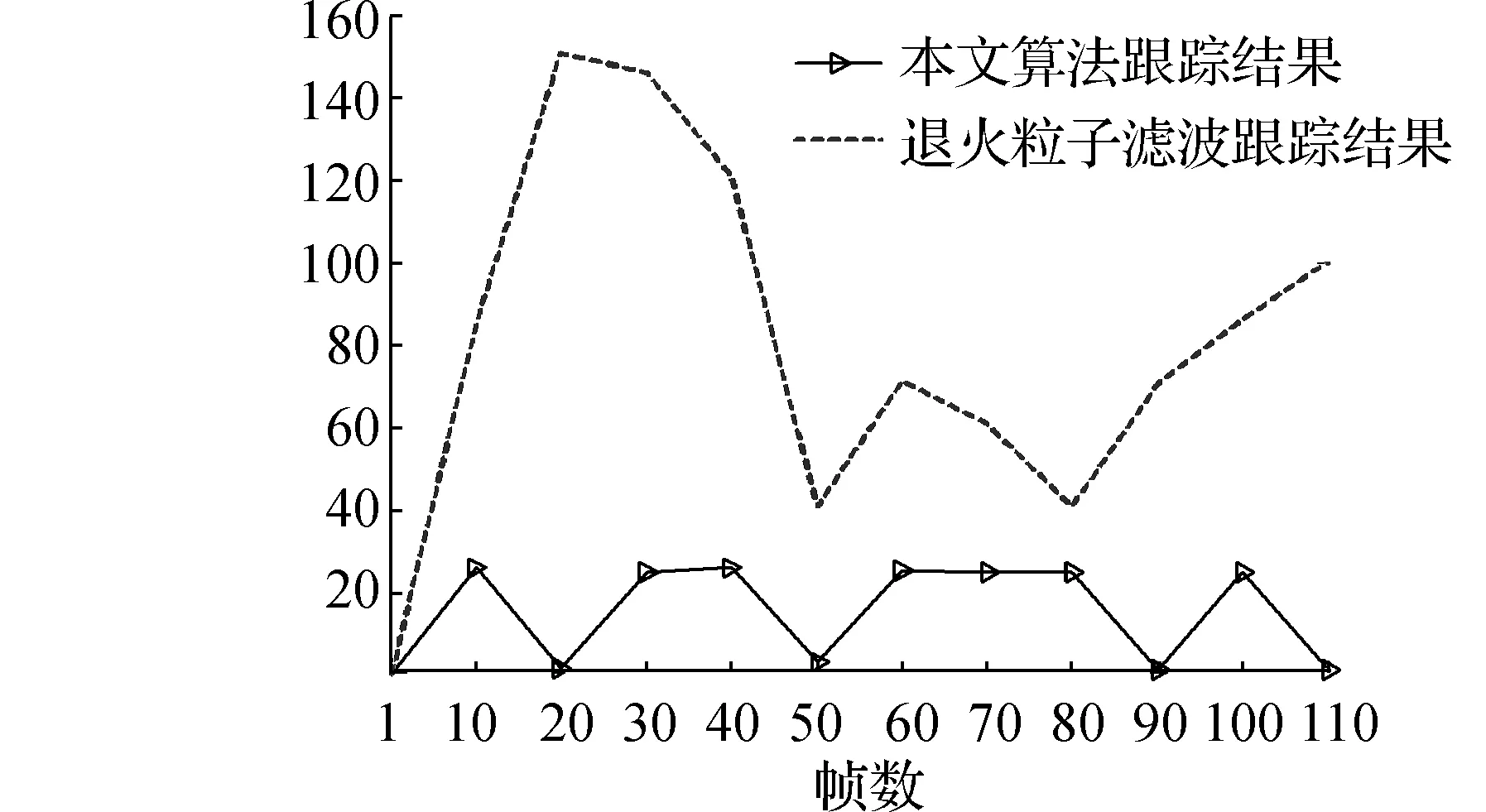
图5 两种算法关键帧执行时间比较

5 结束语

本文提出了均值移动优化的粒子滤波跟踪方法。该算法通过使用尺度和方向自适应的均值移动算法对粒子进行了有效的传播，有效解决了粒子的退化问题，增强了粒子滤波跟踪的抗干扰能力和跟踪精度。

[1]E. Maggio,A. Cavallaro,Hybrid particle filter and Mean Shift tracker with adaptive transition model[J]. Proc. Int. Conf. Acoustics,Speech,and Signal Processing，2005.

[2]朱明清，王智灵，陈宗海，等.基于灰色预测模型和粒子滤波的视觉目标跟踪算法[J].控制与决策，2012，(27)1：53-57.

[3]BLACKE DEUTSCHER,REID I. Articulated body motion capture by annealed particle filtering[J]. Proc. IEEE Conf. Computer Vision Pattern Recognition,2000.

[4]KHAN Z H,GU I Y. Robust visual object tracking using multi-mode anisotropic mean shift and particle filters[J]. IEEE Transactions on Circuits and Systems for Video Technology.2011,(21)1,74-87.

[5]KOICHIRO D,OKI K,TAKAYUKI O. Object tracking by the mean-shift of regional color distribution combined with the particle-filter algorithm[J]. In: Proc 17th Internat. Conf. on Pattern Recognition,2004,vol. 3,506-509P.

[6]NING J,ZHANG L,ZHANG D,et al. Scale and Orientation Adaptive Mean Shift Tracking[M]. in IET Computer Vision. 2010,1-23P .

[7]BIRCHFIELD S T,RANGARAJAN S. Spatiograms Versus Histograms for Region-Based Tracking[J]. Proc. CVPR,June 2005,1158-1163P.

[8]王亚东，雷国华，安波，等.一种仿人足球机器人视觉系统环境特征获取与识别方法[J].黑龙江工程学院学报：自然科学版，2013，27(2)：68-71.

[责任编辑：郝丽英]

Particle filter target tracking method optimized by mean shift

CHU Hong-xia,SI Jin-long,SONG Qi-chao,YU Hao-yang，HAN Jing,ZHANG Peng,QIN Jie

(College of Electrical and Information Engineering,Heilongjiang Institute of Technology,Harbin 150050,China)

In order to achieve the effective dissemination of the particle set and overcome the degradation of particle filter tracking,a particle filter target tracking algorithm optimalized by Scale and Orientation Adaptive Mean Shift is proposed. Considering improved mean shift as an optimization mechanism of particle propagation,the particles can be effectively dispersed and clustering,so the degradation problems can be effectively solved. Finally,this method is applied to the real image sequences. Experiments show that the performance and efficiency of the algorithm are significantly better.

mean shift;partilce filter;adaptive;tracking

2014-05-23

哈尔滨市科技局科技创新人才研究专项资金项目(RC2014QN009012);黑龙江省教育厅科学技术研究项目(12531528);黑龙江工程学院大学生创新训练项目(201311802100);黑龙江工程学院博士科学研究基金资助项目(2012BJ20)

初红霞(1976-),女,讲师,博士,研究方向：模式识别，计算机视觉.

TP391

A

1671-4679(2014)05-0035-04