混沌微粒群优化算法及其在非线性函数参数估计中的应用

曹体涛，罗 刊

(中国中铁二院工程集团有限责任公司，四川 成都 610031)

混沌微粒群优化算法及其在非线性函数参数估计中的应用

曹体涛，罗 刊

(中国中铁二院工程集团有限责任公司，四川 成都 610031)

混沌微粒群优化算法是在微粒群优化算法的基础上引入混沌思想，提高算法的局部搜索能力，具有良好的性能。主要介绍微粒群算法的原理以及混沌优化思想，最后结合求解平面度误差证明混沌微粒群算法在非线性函数参数估计中的有效性及应用前景。

微粒群优化算法；混沌原理；参数估计；平面度误差

微粒群优化算法(PSO)是美国心理学家Kennedy和电器工程师Eberhart受鸟类觅食行为的启发而提出的一种基于群体智能的新的进化算法[1]。该算法首先随机产生一定数量的微粒子，然后再通过迭代计算不断地调整自己的位置。在每一次迭代过程中，微粒子跟踪两个极值：一个是自身的最佳位置，另一个是群体最佳位置。PSO算法通用性强，而且原理简单容易实现，并能利用个体局部信息和群体全局信息指导搜索。但是，PSO算法也存在着一些缺点，算法的局部搜索能力不强，容易陷入局部极小解。而混沌思想通过混沌搜索的轨道遍历性，能够避免搜索陷入局部极小解的情况发生。

本文介绍了将混沌原理与PSO算法结合的混沌微粒群优化算法(CPSO)[2]，通过基于混沌机制的局部搜索来增强算法的局部搜索能力，提高算法的性能。并利用CPSO算法求解平面度误差，说明CPSO算法在进行非线性目标函数参数优化中的有效性和准确性。

1 混沌微粒群优化算法介绍

1.1 微粒子算法介绍

微粒子算法是一种基于群体智能的随机寻优算法。微粒子算法首先在可行解空间随机产生一组带速度和位置的微粒群，粒子在每一次的进化过程中跟踪两个极值：自身的最佳位置和群体最佳位置。在d维搜索空间，把第i个粒子的位置和速度分别表示为：Xi=[xi，1,xi,2,…，xi,d]和Vi=[vi，1,vi,2,…,vi,d]。然后根据计算得到的各微粒的目标函数值，更新在每次进化后的每个微粒所经过的最佳位置Pi=[Pi,1,Pi,2,…,Pi,d]以及群体的最佳位置Pg。对于每一次迭代，各微粒的速度和位置的更新公式为

(1)

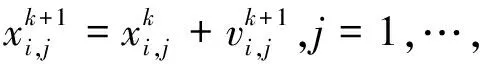
(2)

式中：w为惯性权因子，c1和c2为正的加速常数，r1和r2为在0～1之间均匀分布的随机数。

式(1)中，惯性权因子在决定下一次进化过程中微粒的速度起到了很大作用，因此，惯性权的选择直接影响算法的搜索性能。在此，采用自适应的惯性权系数，它能够根据目标函数值动态地调节惯性权，有利于提高算法的全局搜索能力

(3)

式中:wmax和wmin分别代表w的最大值和最小值，f为当前目标函数值，favg和fmin分别为所有微粒的平均值和最小目标值。

微粒子群算法流程如图1所示。

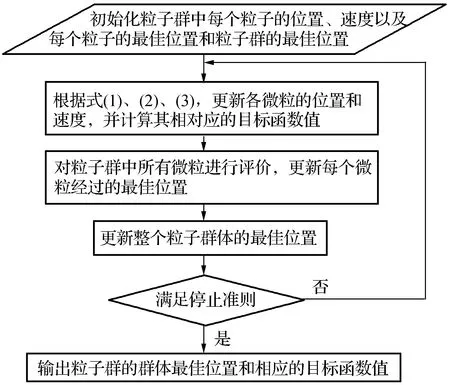
图1 微粒子群算法流程

1.2 混沌优化思想

混沌优化的主要思想是对给定的函数，通过将搜索过程对应为混沌轨道的遍历过程，利用混沌动态特性来实现对解空间的搜索。最常用的混沌序列发生器[3]

xk+1=4xk(1-xk),0≤x0≤1.

(4)

当x0∉{0,0.25,0.5,1}时，式(4)的映射所产生的序列呈现出混沌的动态特征，初始变量的微小变化将导致后续轨道的巨大不同。

i=1,2,…,n;j=1,2,…,d.

(5)

式中:n为粒子个数，d为搜索空间维数，xmin,j和xmax,j分别为第j维变量的搜索上下界。

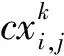
(6)

1.3 混沌PSO算法

在标准微粒子群算法的进化过程中，算法每迭代一次就更新一次所有粒子的速度、位置和目标函数值，因此，在每次更新的过程中引入混沌机制，对微粒子群中的最佳微粒进行混沌搜索。本文采用的混沌PSO算法步骤为：

1)初始化粒子群中每个粒子的位置、速度以及每个粒子和粒子群的最佳位置；

2)根据式(1)、(2)、(3)，更新各微粒的位置和速度，并计算其相对应的目标函数值；

3)对粒子群中所有微粒进行评价，更新每个微粒经过的最佳位置；

4)更新整个粒子群的群体最佳位置；

5)对群体的最佳微粒执行混沌局部搜索(认为拥有最佳目标函数值的粒子为群体的最佳微粒)，然后更新这个微粒的最佳位置和粒子群的群体最佳位置；

6)如果算法满足停止准则，则输出粒子群的群体最佳位置及相应的目标函数值。否则，算法流程转向2)继续进化。

混沌PSO算法是在PSO算法基础上的一个改进，是对两者的一个综合。用PSO算法主要进行全局搜索，而混沌搜索则主要根据PSO算法的结果执行局部搜索，这种混合方法更好地平衡了算法的全局搜索和局部搜索能力，从而提高整体算法的快速性、有效性以及鲁棒性。

2 混沌PSO算法在非线性目标函数参数估计中的应用

利用混沌PSO算法可以对一些复杂非线性函数参数进行估计[4，9]，本文以求解平面度误差为例，运用混沌PSO算法进行平面度误差的计算，并与其他方法的结果相比较，来说明混沌PSO算法的有效性。

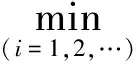
(7)

在算例中，采用参考文献[5]给出的用于平面度误差评定的一组测量数据，见表1。设置迭代次数为500，种群大小为20，粒子维数为3，惯性权因子下限为0.2，惯性权因子上限为1.2，加速常数C1和C2取为2。选取最小二乘的结果对粒子进行初始化，位置范围为-10～10。根据目标函数(7)，即可求得f(a,b)的最小值。

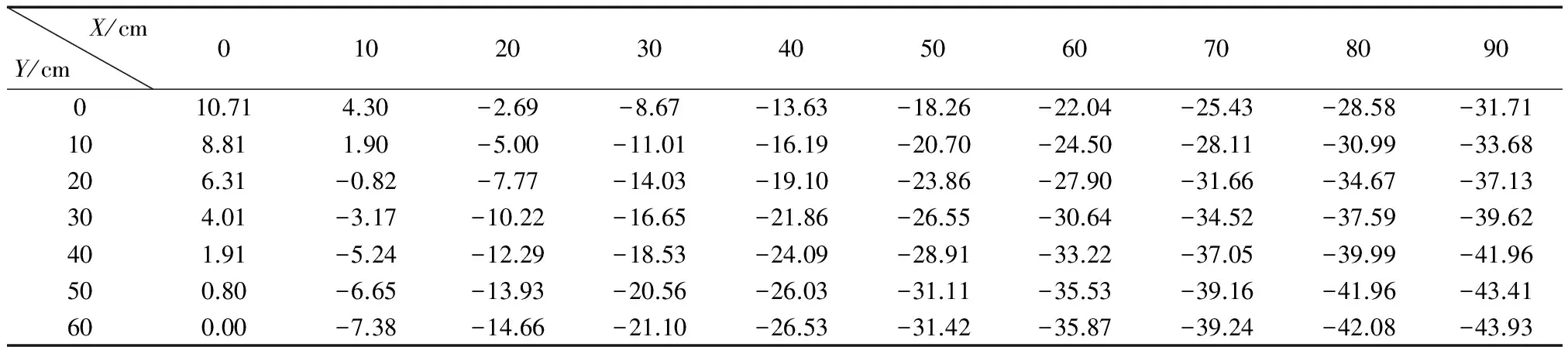
表1 待拟合平面点原始数据 μm

本文采用VC++进行程序设计[6]，通过对表1测量数据计算，得到平面误差为7.75 μm，a=-0.487 8 μm·cm-1,b=-0.204 4 μm·cm-1。利用本文介绍算法计算结果与参考文献[7]中的结果对比见表2。

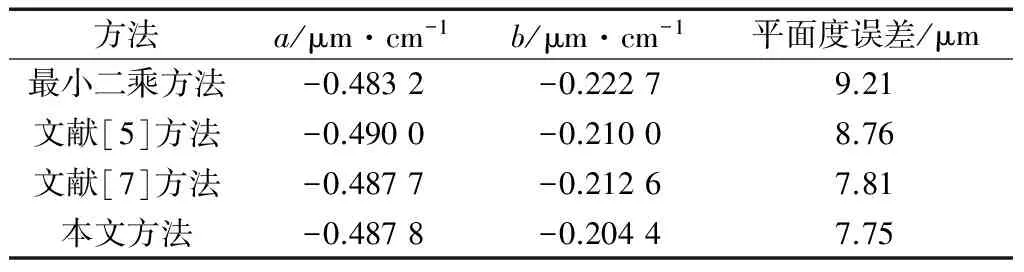
表2 计算结果对比

从表2可以看出，CPSO算法所得到的平面度误差最小，且只迭代了500次，说明本文介绍算法的有效性和快速性。由于该算法具有全局和局部搜索能力，可以保证搜索到全局的最优解，进而准确求得平面度误差。

3 结束语

通过求解平面度误差的计算应用，可以看出CPSO算法在进行非线性函数参数优化中具有较大优势。通常利用的最小二乘法是对非线性函数线性化后再平差求解，其线性化过程较麻烦且不够准确，但粒子群算法较好地解决了这些问题。与其他智能优化算法相比，PSO算法原理简单，参数个数较少，是新一代的群体智能优化算法，有广阔的发展前景[8-10]，PSO算法在与混沌优化法结合后表现出了更优秀的性能。虽然CPSO算法目前的实际应用还相对较少，但在一些专业领域，已经将其应用到图像处理以及变形监测的分析、预报中，相信在不久的将来会得到推广。

[1]KENNEDY J,EBERHART R C.Particles warm optimization[C]. Perth,Australia:Proceedings of the IEEE International Conference on Neural Networks,1995：1942-1948.

[2]王凌,刘波.微粒群优化与调度算法[M].北京:清华大学出版社,2008：58-135.

[3]MAY R M. Simple mathematical models with very complicated dynamics[J]. Nature,1976,261:459-467.

[4]路志强,杨文海,黄腾,等.粒子群算法及其在暴雨强度公式参数优化中的应用[J]. 南水北调与水利科技,2008,6 (3):72-73.

[5]HUANG S T,FAN K C,WU J H. A new minimum zone method for evaluating flatness error [J]. Precision Engineering,1993,15(1):25-32.

[6]文瑾.基于VB语言的粒子群优化算法描述[J]. 昆明大学报,2006,17(4):39-40.

[7]崔长彩,车仁生,罗小川,等.基于实数编码遗传算法的平面度评定[J].光学精密工程,2002,10(1):36-39.

[8]李宁,付国江,库少平,等.粒子群优化算法的发展与展望[J]. 武汉理工大学学报：信息与管理工程版,2005,2(2):26-29.

[9]姜焰鸣,刘桂雄.平面度误差粒子群算法评定的不确定度评估[J].中国测试,2013,39(1):13-16.

[10]曾凯,姜岩,吴玮,等.神经网络在GPS高程拟合中的应用[J].黑龙江工程学院学报:自然科学版,2013,27(3):12-16.

[责任编辑：郝丽英]

Chaoticparticleswarmoptimizationalgorithmanditsapplicationtononlinearfunctionparameterestimation

CAO Ti-tao LUO Kan

(China Railway No.2 Engineering Group Co. Ltd.，Chengdu 610031,China)

Chaotic particle swarm optimization algorithm is an algorithm based on the introduction of chaotic thought,which improves the algorithm’s local search capability,and has a good performance. It mainly introduces the principle of particle swarm optimization,as well as the chaos optimization idea,and finally combining with the two to solve flatness error is proves the effectiveness and the general application prospects of this algorithm for parameter estimation in nonlinear function.

particle swarm optimization algorithm;chaotic principle;parameter estimation;flatness error

2014-04-03

曹体涛(1977-)，男，工程师，研究方向：精密工程测量.

TP18

A

1671-4679(2014)05-0054-03