酉矩阵束方法在波达方向估计中的应用

刘述强

(黑龙江工程学院，黑龙江 哈尔滨 150050)

酉矩阵束方法在波达方向估计中的应用

刘述强

(黑龙江工程学院，黑龙江 哈尔滨 150050)

空间目标方位估计技术广泛应用于众多军事及国民经济领域，其中矩阵束方法(Matrix Pencil，MP)是广大学者研究的热点技术之一。首先对传统矩阵束方法的基本原理进行介绍，并针对传统方法在低信噪比条件下的方位估计精度明显下降问题，结合酉变换技术，对传统方法进行改进。理论分析及计算机仿真研究表明：基于酉变换的矩阵束方位估计方法在低信噪比条件下具有更高的估计精度及空间目标分辨能力，同时也表明该方法具有更优的有效性和正确性。

空间目标方位估计；矩阵束方法；酉变换技术；低信噪比条件

空间目标方位估计(Direction of Arrival，DOA)技术是阵列信号处理的一个重要分支，广泛应用于雷达、声呐、通信、勘探、医学工程等众多军事及国民经济领域[1]。近几十年，方位估计技术的研究日新月异，涌现出了大量的新思想、新方法，取得了长足的进步。1967年，Burg首次将线性预测法用于估计信号的入射方向，这就是著名的最大熵谱法(Maximum Entropy Method，MEM)。1979年，Schmidt R O等人提出了多重信号分类MUSIC算法，促进了子空间类算法的兴起，开启了高分辨方位估计技术的新纪元[2]。

除此之外，属于谐波恢复类的矩阵束算法(Matrix Pencil，MP)受到广大研究者的青睐，该算法不受相干源限制，且无需估计协方差矩阵，可在单次快拍基础上实现目标方位估计，算法复杂度低，满足工程实时性要求，但MP算法受噪声影响较大，在低信噪比条件下的方位估计精度明显下降。为克服噪声的影响，广大学者进一步研究基于多快拍的矩阵束算法，以期提高算法的估计精度，但仅在有限的程度上改善了算法的性能[3]。

究其原因，传统的矩阵束算法仅利用阵元上的观测数据，而没有利用共轭的观测数据。由于一个复观测数据和它的共轭包含不同的信息，如果能够同时利用两者，则可利用的数据长度等于增加了一倍，显然，这将提高传统MP算法的估计精度并改善其估计性能。针对这一问题，酉变换恰恰可实现同时利用观测数据和共轭观测数据的目的[4]。基于此，本文将酉变换与传统矩阵束算法相结合，研究一种基于酉变换的矩阵束方位估计方法，并通过仿真实验验证了该方法的有效性。

1 矩阵束算法

1.1 传统矩阵束算法

考虑一个由N个基元组成的均匀线阵，阵元间距为d，设空间中存在M个波长为λ的远场窄带相干声源，时间平稳且N>M，为讨论方便，忽略时间因子及噪声影响，则阵元接收信号可以表示为

k=0,…,N-1.

(1)

通过式(1)，构建Hankel矩阵

(2)

其中，L为束参数。进一步构造Ya和Yb

(3)

(4)

求得矩阵束[Ya,Yb]的广义特征值zi，即可得信号的方位估计结果。以上为基于单快拍的MP算法，下面介绍多快拍MP算法[5]。

以每个快拍数据分别构建数据Hankel矩阵

(5)

进一步将构建的N个单快拍Hankel矩阵组成一个多快拍Hankel矩阵

YE=[Y0,Y1,…,YN-1](N-L)×NL.

(6)

根据YE得到两个子阵YE1和YE2，对该两个子阵进行广义特征值分解，并根据MP算法的基本原理可得空间信源方位估计结果[3]。

1.2 酉矩阵束算法

传统的矩阵束算法存在一个缺陷：其仅利用阵元上的观测数据，而没有利用共轭的观测数据。本文将酉变换与传统矩阵束算法相结合，同时利用复观测数据和其共轭信息，提高传统MP算法的估计精度并改善其估计性能。

根据广义特征值分解

Ya-λYb=ZaR0[Z0-λI]Zb.

(7)

式(7)等价为

Ya-λYb=J2Y-λJ1Y.

(8)

其中:Ya=J1Y，Yb=J2Y，J1与J2为选择矩阵

Ya-λYb=J2Y-λJ1Y=0.

(11)

由式(11)可得

J2Y=λJ1Y.

(12)

根据Centro-Hermitian矩阵的相关定理[6]，QQH=I；QHYQ=Xr为实数，进一步可得

QHJ2QQHYQ=λQHJ1QQHYQ,

(13)

QHJ2QXr=λQHJ1QXr.

(14)

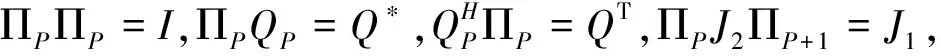
(15)

根据式(14)和(15)，可得

(QHJ1Q)*Xr=λQHJ1QXr.

(16)

将实部和虚部分离，进一步得到

[Re(QHJ1Q)-jIm(QHJ1Q)]Xr=

[Re(λ)+jIm(λ)][Re(QHJ1Q)+

jIm(QHJ1Q)]Xr.

(17)

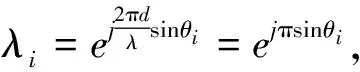
Re(λi)=cos(πsinθi),

(18)

Im(λi)=sin(πsinθi).

(19)

故

Im(QHJ1Q)Xr.

(20)

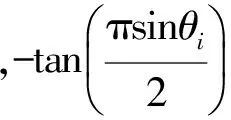
2 仿真分析

下面对常规MP算法及其改进算法进行计算机仿真分析。

仿真1：信号频率f=200 kHz，信号脉宽τ=0.05 ms，阵元数N=10，阵元间距为半波长，对于单信源目标情况，声源入射方向θ=30°。对于相干双信源目标情况，预设信源入射方向θ1=0°、θ2=15°，信噪比均为10 dB。数据总长共有80个数据快拍，每个估计结果均由1个快拍数据完成，则共进行80次MP估计。估计结果如图1所示。

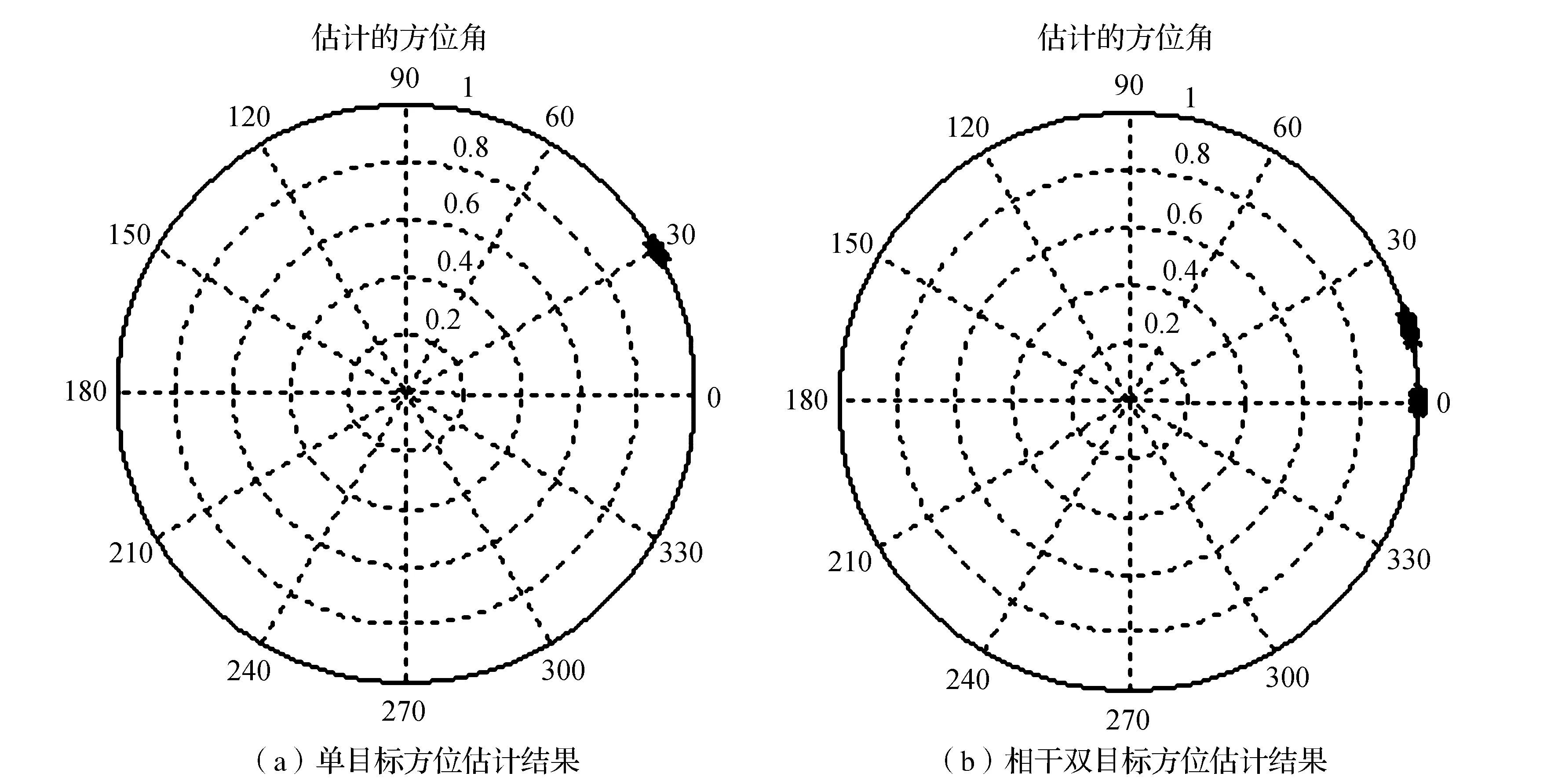
图1 MP算法的方位估计结果

图1(a)和(b)分别为单目标和双目标方位估计结果，从仿真结果可以清楚看出，在此仿真条件下，MP算法能够准确估计出目标的方位。

仿真2：分析单次快拍MP算法的双目标估计性能。信号频率f=200 kHz，8倍采样，脉宽τ=0.05 ms，阵元数8，阵元间距半波长，信号入射方向θ1=0°、θ2=10°，信号幅度分别为Amp1=0.8、Amp2=0.8，功率信噪比5 dB，采样快拍数80个，采用单次快拍数进行方位估计。

从图2可以看出，在双目标入射方位角较近的条件下，基于单次快拍数的常规MP算法的方位估计结果偏差较大，不能有效反映出声源的正确方位。究其原因是由于常规MP算法本身仅采用阵元域单次快拍处理，抗噪声干扰能力较差，算法性能下降，严重影响了该算法的实际工程应用。

图2 常规MP算法单次快拍估计结果

仿真3：为了克服单次快拍的制约，可采用多快拍MP方位估计算法，进一步对多快拍MP算法的性能进行计算机仿真分析。仿真条件与仿真2条件相同，讨论基于多次快拍的MP算法对空间双相干信源的估计性能。图3为基于多次快拍的MP算法仿真估计结果，估计空间两相干信源的方位分别为 5.323 9°和 24.746 5°，幅度分别为 0.790 6和0.340 1。

图3 常规MP算法多次快拍估计结果

与基于单次快拍的估计结果相比较可以看出，多快拍MP算法在一定程度上改善了单快拍MP算法的估计性能，方位估计结果的收敛性明显改善，但仍然有较大的方位估计偏差。

为进一步提高MP算法的性能，采用酉变换技术，在提高算法实时性的同时，降低算法信噪比门限，可有效提高算法的性能。

仿真4：下面进一步对酉矩阵束算法的性能进行计算机仿真分析。仿真条件与仿真3相同，讨论基于酉变换的多次快拍MP算法对双相干信源方位估计的性能。图4为基于酉变换的多次快拍MP算法仿真估计结果，估计空间两相干信源的方位分别为 0.748 1°和 11.368 0°，幅度分别为 0.863 2和 0.796 9。

图4 酉矩阵束估计结果

与基于多次快拍的估计结果相比较可以看出，基于酉变换MP算法的方位估计结果与仿真条件基本吻合，有效地提高了算法的性能。

3 结束语

本文研究了一种基于酉变换技术的矩阵束方位估计方法，针对传统方法在低信噪比条件下的方位估计精度明显下降这一问题，结合酉变换技术，

对传统方法进行改进。该方法有效地克服了低信噪比对传统矩阵束算法性能的影响和制约，具有更高的方位估计精度，更低的方位估计误差。同时，理论研究和计算机仿真分析结果表明该方法的正确性和有效性。

[1]HAMID KRIM，MATS VIBERG．Two decades of array signal processing research[J]．IEEE Signal Processing Magazine,1996：798-802.

[2]王永良，陈辉，彭应宁,等．空间谱估计理论与算法[M]．北京：清华大学出版社，2004:5-12.

[3]NURI YILMAZER，JINHWAN KOH,TAPAN K SARKAR．Utilization of a Unitary Transform for Efficient Computation in the Matrix Pencil Method to Find the Direction of Arrival[J]．IEEE Transactions on Antennas and Propagation，2006，54(1):175-181.

[4]NURI YILMAZER,TAPAN K SARKAR ．Efficient Computation of the Azimuth and Elevation Angles of the Sources by Using Unitary Matrix Pencil Method (2-D UMP)[J]．IEEE，2006:1 145-1 148.

[5]胡海波，刘柏森，许银，等．基于小波变换的语音增强研究[J]．黑龙江工程学院学报：自然科学版，2011,25(1)：43-46.

[6]卜长江，罗跃生．矩阵论[M]．哈尔滨：哈尔滨工程大学出版社，2003:156-184.

[责任编辑：郝丽英]

ApplicationofunitarymatrixpencilmethodtoDirection-of-Arrivalestimation

LIU Shu-qiang

(Heilongjiang Institute of Technology,Harbin 150050,China)

Direction-of-Arrival (DOA) estimation techniques have been widely applied to many military and civil economy fields. Especially,matrix pencil method is one of the hottest technologies for general scholars. First,it introduces the basic theory of traditional matrix pencil method. To the problem of a dramatic decline of DOA estimation accuracy for traditional method in low-SNR (Signal Noise Ratio) condition,existing method is improved in combination with the unitary transformation technology. The study of theory analysis and computer simulation show that unitary matrix pencil method in DOA estimation has higher estimation accuracy and space resolution under scenarios of low-SNR,and proves that the proposed method is effective and correct.

DOA;MP Method;unitary transformation technology;low-SNR condition

2014-04-19

刘述强(1982-)，男，讲师，研究方向：电气工程.

TN821.8

A

1671-4679(2014)05-0046-04