基本地貌形态数学模型的改进

钟业勋,胡宝清,朱重光

(1.广西师范学院 北部湾环境演变与资源利用省部共建教育部重点实验室 资源与环境科学学院，广西 南宁 530001；2.广西测绘地理信息局，广西 南宁 530023；3.中国科学院遥感应用研究所，北京 100101)

基本地貌形态数学模型的改进

钟业勋1，2,胡宝清1,朱重光3

(1.广西师范学院 北部湾环境演变与资源利用省部共建教育部重点实验室 资源与环境科学学院，广西 南宁 530001；2.广西测绘地理信息局，广西 南宁 530023；3.中国科学院遥感应用研究所，北京 100101)

以邻域、边界等拓扑学概念为基础，引入环状邻域和分离型邻域等概念，根据任意点对地貌特征点的高差所满足的不同条件，分别推导了山、洼地、鞍部、盆地、高原、岛屿等基本地貌形态的数学模型。

拓扑学；邻域；边界；山；鞍部；高原；数学模型

地表形态又称地形或地貌。规模不同、形态各异的地貌，是在不同的地球内、外营力作用下形成的。内营力是地球内部能量所发生的作用，主要是指地壳运动。地表的基本地貌或原生地形，是由内力作用造成的。外营力因素对地表的作用，总的说来就是不断起着剥蚀作用与堆积作用，它是趋向于破坏和削平那些由内力作用而产生的隆起部分，同时把这些破坏了的碎屑物质堆积到海洋中去。外力修饰地表的基本形态，又称为次生地形[1-2]。地貌测绘属基础测绘，它是国家基本比例尺地图表示的重要内容之一。研究山、平原、高原、盆地、岛屿等基本地貌形态的数学模型，在信息处理自动化、快速化和集成化的现代测绘技术环境下，对相关软件的研发和应用有重要的意义。笔者在文献[3-5]中曾给出了一些基本地貌形态的数学模型，由于还有岛屿等概念尚未涉及，一些模型还有改进的必要。所以本文再提出新的研究成果。

1 导出基本地貌形态表达式的拓扑学概念

定义1：内点和内部，外点和外部[6]设A是拓扑空间X的子集，x∈X,如果存在开集x∈V⊂A，则称x是A的内点。A的所有内点的集合称为A的内部，记作A°。如果a是A′的内点，则称a是A的外点。A的所有外点的集合称为A的外部，记作Ae。

定义2：边界[7]设A是拓扑空间X的子集，x∈X,如果在x的任意邻域中既有A的点又有X-A的点，则称x是A的边界点。A的边界点全体所成的集合，称为A的边界，记为BdA。集A的边界可表示为

(1)

定义3：环状正邻域 ∃地貌基准点p∈S，若p的邻域Np满足

∀i∈Np⇒Hi-Hp≥0∧S∈W°i|Wi={Hi}|.

(2)

定义4：环状负邻域 ∃地貌基准点p∈S，若p的邻域Np满足

∀j∈Np⇒Hj-Hp≤0∧S∈W°j|Wj={Hj}|.

(3)

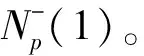
定义5：分离型正邻域 ∃地貌基准点p∈S，若任意点i满足

∀i∈Np⇒i′∈Np.s.t.Hi=Hi′,

Hi-Hp≥0|Wi∩Wi′=Ø|.|

(4)

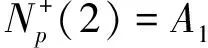
(5)

其中Wi={Hi}∈A1,Wi′={Hi′}∈A2。Wi∩Wi′=Ø。Wi和Wi′称为正向共轭等高线。

定义6：分离型负邻域 ∃地貌基准点p∈S，若任意点j满足

∀j∈Np⇒j′∈Np.s.t.Hj=Hj′,

Hj-Hp≤0|Wj∩Wj′=Ø|.

(6)

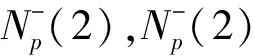
(7)

其中Wj={Hj}∈B1,Wj′={Hj′}∈B2,Wj∩Wj′=Ø。Wj和Wj′称为负向共轭等高线。

2 基本地貌形态的数学模型

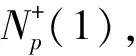
(8)

(9)

(10)

Wc=Wi∪Wi′∪Wj∪Wj′

(11)

称为鞍部的等高线图形。

定义10:盆地∃基准地貌区域A，A的边界为BdA，A的外部为Ae，地貌特征点p∈BdA，若满足

∀i∈A⇒Hi-Hp≤|K|∧∀i∈Ae⇒

Hi-Hp>K.

(12)

则称D=A∪BdA∪Ae为以A为底起伏度为K和周边为Ae的盆地。不同的A，BdA，Ae组合表达着不同的盆地形态。

定义11:高原 ∃基准地貌区域A，A的边界为BdA，A的外部为Ae，地貌特征点p∈BdA，若满足

∀j∈A⇒Hj-Hp≤|K|∧∀j∈Ae⇒

Hj-Hp

(13)

则称D=A∪BdA∪Ae为以A为主体，A的起伏度为K和周边为Ae的高原。不同的A，BdA，Ae组合表达着不同的高原形态。

定义12：平原 ∃地貌基准点p∈S和p的邻域Np，若满足

∀i∈Np∧i∈S⇒Hi-Hp≤|K|.

(14)

则称S与Np的并集D=S∪Np为起伏度为K的平原。

定义13：岛屿 设w0为基准地貌区域A的下界，p∈A∧p⇔上界，那末，满足下列条件的点i的集合

A={i|∀i| ∈A⇒Hp≥Hi≥0∧Ae∈ 海洋}.

(15)

则称A为以零等高线w0为范围和高程基准，以p为最高点的岛屿。

定义14：群岛 设定名区域D⊃Aj|j∈J|，如果满足

∀Aj⊂D⇒

(16)

则称D为包含J个岛屿和岛屿间间隔不大于K的群岛。

3 结束语

基本地貌形态是国家基本比例尺地图表示的重要内容之一。本文以点集的内部、外部、边界、邻域等拓扑学概念为基础，引入环状正邻域、环状负邻域、分离型正邻域、分离型负邻域等概念，推导了山、洼地、鞍部、盆地、高原、平原、岛屿和群岛等基本地貌形态的数学模型，揭示了这些基本地貌形态的数学本质和内在联系。对此前给出的如山、洼地、鞍部等的数学模型作了改进。本文提出的基本地貌形态的数学模型，对于地理学的理论研究和对相关制图软件的研发和应用有参考价值。

[1]南京大学地理系地貌教研室.地貌学[M].北京：人民教育出版社,1961.

[2]缪启龙.地球科学概论[M].北京：气象出版社,2001.

[3]钟业勋，魏文展，李占元.基本地貌形态数学定义的研究[J].测绘科学，2002,27(3):16-18.

[4]钟业勋，胡宝清，朱根雄.基本地貌形态数学定义体系研究[J]. 桂林工学院学报,2009，29(4):481-484.

[5]钟业勋，胡宝清.山地与平原数学定义的研究[J].黑龙江工程学院学报：自然科学版，2009，23(3):26-28.

[6]程吉树，陈水利.点集拓扑学[M]. 北京：科学出版社，2008.

[7]谷超豪，数学词典[M]. 上海：上海辞书出版社，1992.

[8]李孝传，陈玉清. 一般拓朴学导引[M]. 北京：高等教育出版社，1982.

[9]谷超豪.数学词典[M].上海：上海辞书出版社，1992.

[责任编辑：刘文霞]

Improvement of mathematical model of basic geomorphic form

ZHONG Ye-xun1,2,HU Bao-qing1,ZHU Chong-guang3

(1.key Laboratory of Beibu Gulf Environment Change and Resources Use (Cooperated with Ministry of Education),School of Resource and Environment Science,Guangxi Teachers’College,Nanning 530001,China；2.Guangxi Regional Geographical Information Bureau of Surveying and Mapping,Nanning 530023,China； 3.Institute of Remote Sensing Applications,Chinese Academy of Sciences,Beijing 100101,China)

On the basic topology concepts of neighborhood and boundary,etc. it presents the concept of annular neighborhood and separated neighborhood. In order to satisfy the different conditions of height difference between any point and geomorphic triat point,the mathematical models of basic geomorphic form are deducted for as the mountain,hollow,saddle,basin,highland,islands,etc. respectively.

topology;neighborhood;boundary;mountain;saddle;highland;mathematical model.

2014-06-18

国家自然科学基金资助项目(41361022)；广西科技开发资助项目(2014DD29090)；广西北部湾重大基础专项子课题(2012G1XNSFEA053001)

钟业勋(1939-)，男，教授，研究方向:地图学理论.

P931

A

1671-4679(2014)05-0001-02