下承式钢管混凝土刚架系杆拱桥吊杆断裂动力分析
吴庆雄,余印根,陈宝春
(福州大学 土木工程学院,福州 350108)
中、下承式拱桥由主拱肋(拱圈)、吊杆、桥道系等构件组成。其中,作为中、下承式拱桥的重要承重构件,吊杆起着连接拱肋和桥道系的作用,作用于桥面上的恒载、活载通过桥道系传递给吊杆,并最终作用在拱肋上[1]。因此,吊杆的可靠性、耐久性关系到中、下承式拱桥的安全和正常使用。
然而,吊杆这种索结构对外界的侵害比较敏感,在遭遇突发事件(如爆炸、撞击、火灾、雷击等)、疲劳损伤及锈蚀等作用下,可能出现吊杆断裂,吊杆断裂可能导致桥道系的垮塌,甚至拱肋的局部破坏或整体破坏[2]。2001年11月7日,四川(宜宾市金沙江小南门大桥吊杆发生断裂,导致两端共计长约30 m的桥道系坍塌[3]。2011年4月12日凌晨,新疆库尔勒孔雀河大桥主跨第二根吊杆断裂,造成主跨第三、四、五道主梁掉入河中,长约10 m、宽约12 m桥面发生坍塌[4]。仅事隔三个月,2011年7月14日8时50分,福建武夷山市公馆大桥由于吊杆断裂再度发生连续板垮塌[5]。
如何防止结构因局部破坏引起连续性倒塌问题引起了高度关注。房建领域的学者们提出了很多分析方法和设计建议,并形成了规范或规程,如英国规范[6]、欧洲规范[7]、美国GSA和DoD发布的规程[8-9]。在桥梁工程方面,对于斜拉桥设计计算中考虑了拉索断裂工况,采用去除该斜拉索进行全桥分析,并对主梁的内力和变形进行了限制[10]。但是,对于拱桥,没有相应的去除吊杆进行全桥分析的做法,也没有对桥道系和拱肋的内力和变形进行限制。同时,在计算拉索断裂工况时,只进行静力分析,没有考虑由于吊杆断裂过程中产生的大于静力响应的动力作用。
本文以一座下承式钢管混凝土刚架系杆拱桥为工程背景,采用有限元软件ANSYS/LS-DYNA对吊杆断裂过程进行动力模拟,选取短吊杆断裂和长吊杆断裂两种工况,分析了吊杆断裂前后拱桥各主要承重构件受力状态的动态变化,并对拱桥可能发生的破坏形态进行了讨论。
1 工程简介及有限元模型
1.1 工程简介
某下承式钢管混凝土刚架系杆拱桥的计算跨径150 m,矢跨比1/4.5,拱轴线采用拱轴系数1.167的悬链线,见图1[11]。全桥2片拱肋,拱肋截面为4根上下弦钢管(Φ750×12 mm)和上下平联(1Φ400×10 mm)、腹杆(Φ245×10 mm)焊接成的四肢格构桁式截面,截面高度3 m,宽度2 m,拱脚实腹腔内泵送50号微膨胀混凝土。吊杆采用34对2(61Φ7)双吊杆构造,材料为高强钢丝。桥道系采用以横梁受力为主的桥道系,横梁之间用加劲纵梁连续贯通,全桥共有17片预应力混凝土箱形截面横梁,36片箱型截面加劲钢纵梁。桥面板采用先简支后连续的体系,桥面板与横梁之间采用剪力键连接。
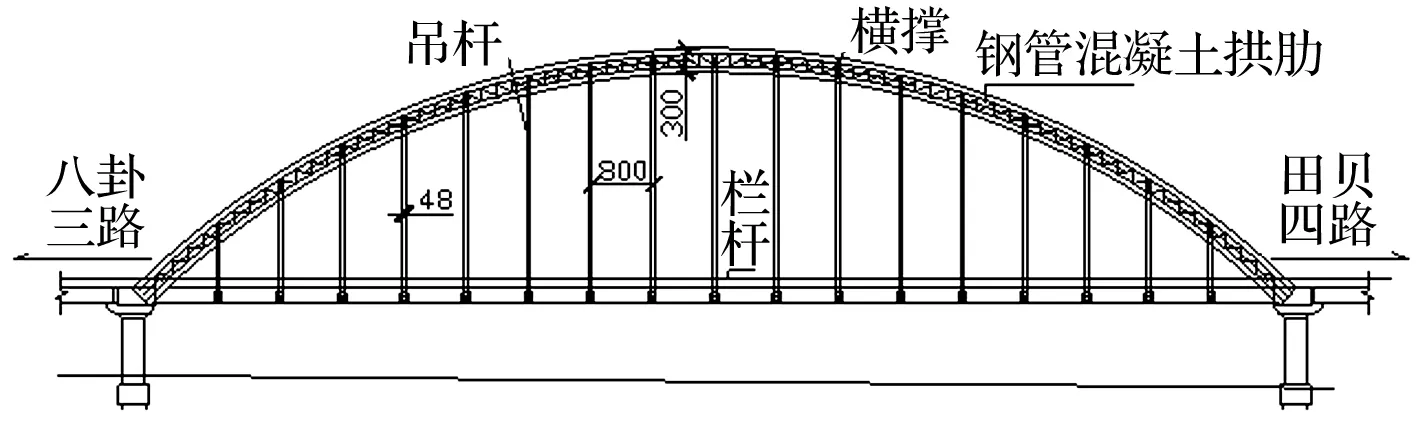
图1 某下承式钢管混凝土刚架系杆拱桥总体布置图
1.2 有限元模型
采用有限元软件ANSYS/LS-DYNA建立全桥三维有限元模型,如图2所示。

图2 ANSYS/LS-DYNA建立的桥梁空间有限元模型
拱肋采用Beam161空间梁单元来模拟,钢管混凝土拱肋的模拟采用了双单元法[12],拱肋共688个单元。横梁、纵梁、横撑、拱肋腹杆及上下平联也采用Beam161单元模拟,全桥端横梁共66个单元,内横梁425个单元,纵梁单元共36个单元,横撑共230个单元,拱肋腹杆528个单元,上下平联352个单元。
吊杆、系杆采用link167模拟,设置杆单元只受拉不受压,每根吊杆或系杆为一个单元,全桥吊杆共68个单元,系杆共8个单元。吊杆编号按照吊杆的位置从一端至另一端依次编为上游侧1#、2#、3#、……33#、34#,下游侧D1#、D2#、D3#、…D33#、D34#。
桥面板为预制空心板,在建模时将整个桥面系模拟为梁格系。桥面板通过有效宽度将其刚度分布于纵梁和横梁上,通过集中质量把其质量分布于桥面节点,不考虑桥面铺装刚度贡献,只将其重量计入桥面板中。采用Beam161单元模拟,全桥桥面板共396个单元。
吊杆下端节点与纵梁节点以及拱脚实心段和桁架式拱肋通过节点耦合功能处理它们之间的主从关系。边界条件根据实桥支承条件进行设置,四个拱脚处为刚接。由于纵梁、横梁和吊杆组成一漂浮体系,将纵梁与帽梁连接处纵桥向约束释放,以使桥面系不承受拉力,也使拱肋产生的推力全部由系杆承受。
1.3 有限元模型的验证
为了验证建立的计算模型的正确性,采用文献[11]的静载和动载试验数据进行校核。取有关拱肋的试验工况(工况1、2和3)进行讨论,其中工况1、2为南侧拱肋1/4截面最大正弯矩和拱脚截面最大负弯矩布载、工况3为南侧拱肋拱顶最大正弯矩布载。
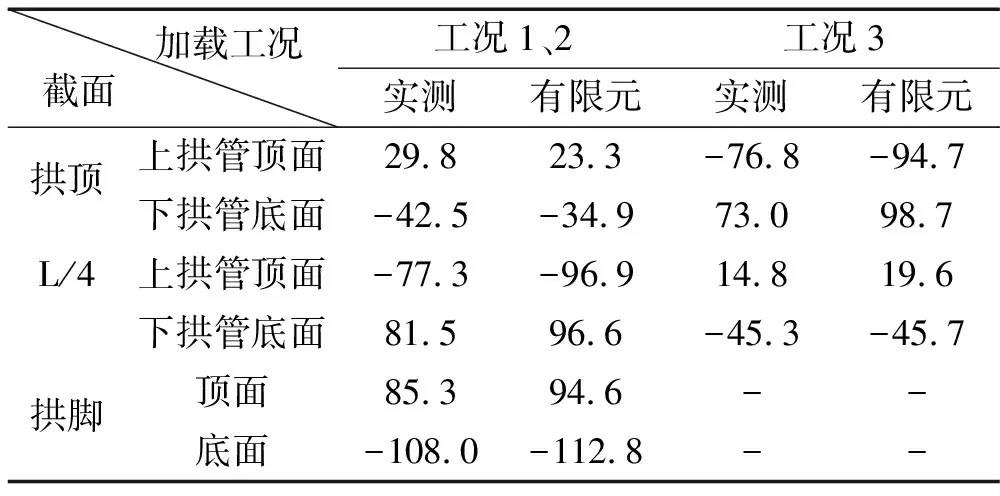
表1 拱肋应变结果对比表(单位:με)
表1为各控制截面上拱肋顶面和下拱肋底面的应变。可以看出,有限元结果与实测结果大部分差值不超过15%。图3为拱肋挠度曲线。可以看出,有限元计算挠度的变化趋势与实测结果一致,挠度计算值与实测值的差值不超过15%。表2为该桥的面外、面内基频,有限元计算基频与实测结果差别不大。因此,通过对静动载试验下有限元计算结果和实测结果的比较可知,荷载试验现场测试结果与有限元模型计算结果比较接近,从而证明了本文建立的有限元模型的可靠性。
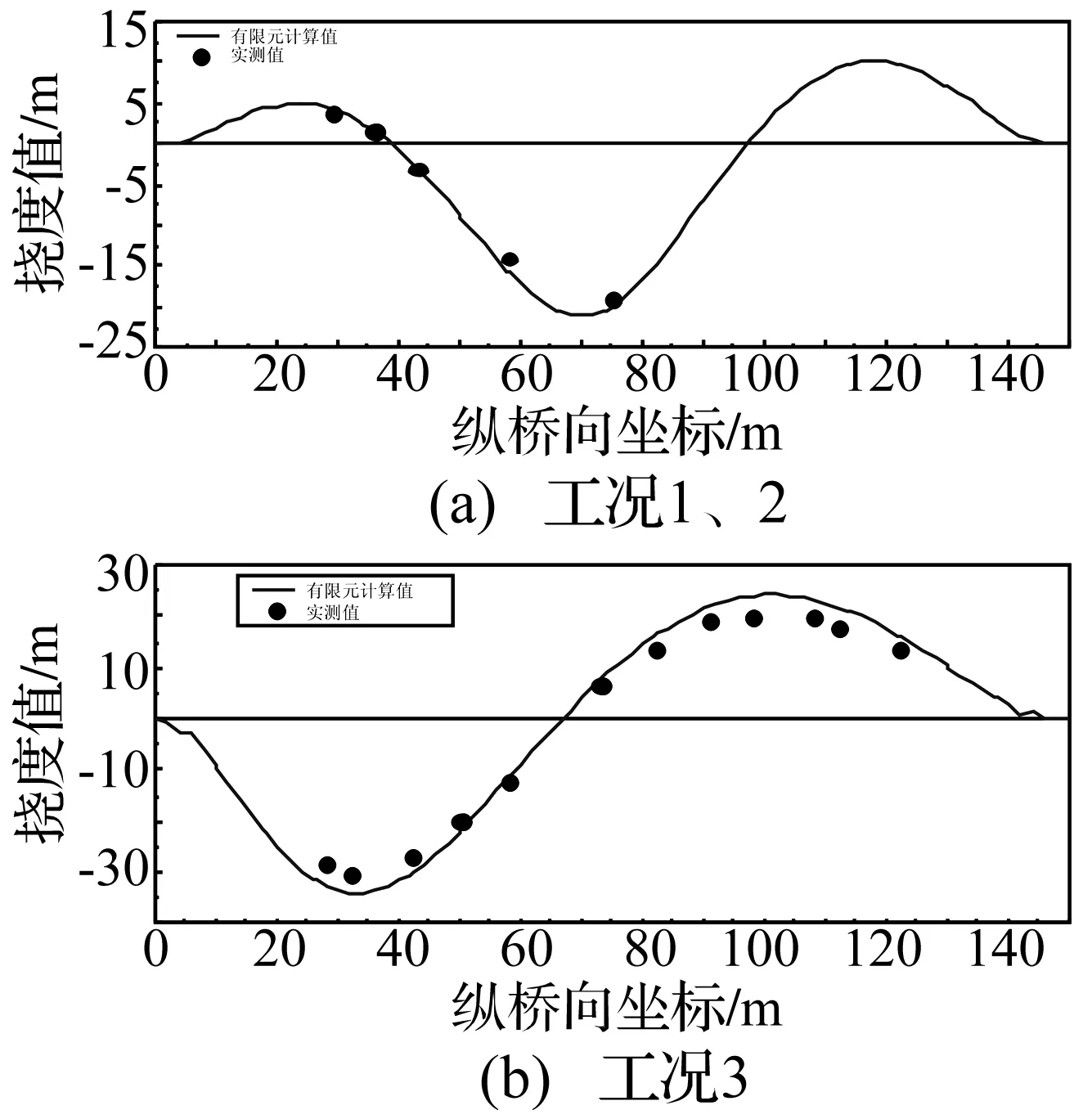
图3 拱肋挠度曲线
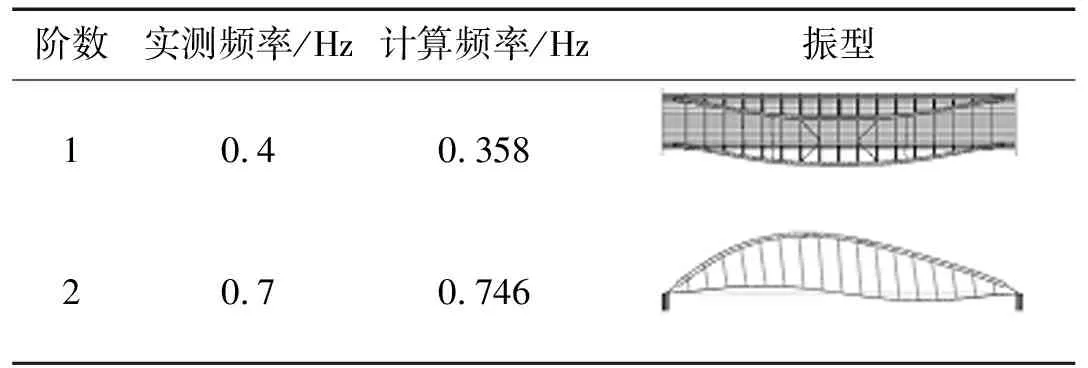
表2 主要模态对比表
2 吊杆断裂动力分析方法
2.1 吊杆断裂模拟方法
吊杆断裂可能引起桥梁结构的连续性倒塌,在结构的连续性倒塌研究中,需要考虑结构的动力响应,但是这个响应并不是由结构所承受的动力荷载引起的。事实上,在结构连续性倒塌的过程中,结构并没有承受具体的动力荷载(构件倒塌坠落的冲击荷载除外),结构的初始动力响应是由于几何突变所引起的构件振动造成的。这是连续性倒塌分析的动力计算与常规动力计算的本质区别[13]。因此,吊杆断裂引起的结构动力计算的关键在于如何恰当的模拟吊杆的失效,以获得最接近实际情况的结构动力响应。
本文主要采用接触—碰撞界面的处理算法来进行吊杆断裂的动力过程模拟,主要利用ANSYS/LS-DYNA中的接触碰撞处理功能。接触碰撞处理是该软件最主要的功能,被广泛运用于接触碰撞计算。当柔性吊杆受到横向碰撞时,吊杆力将会增大,通过控制碰撞体的速度,可以使吊杆力在短时间内达到某一个较大值。吊杆力的增大将对拱肋和桥道系产生扰动并产生竖向冲击的作用,如果吊杆在碰撞过程中内力达到某一个值时断裂,则相当于在该吊杆处施加了一个相应的断索冲击作用[14]。
碰撞体采用实体单元建模,主要考虑其在碰撞过程中动能的贡献,而不考虑与桥面板的相互作用。在模拟时,碰撞体质量及速度的控制以能使吊杆达到相应的内力值为标准。
在碰撞过程中,碰撞体与吊杆的接触采用单面接触的方式。采用这种方式,在程序中将自动判定模型中发生接触的表面。在模拟过程中主要采用的计算方式是重启动的方式,本文在模拟时使用的重启动方式有以下两种:
(1) 小型重启动:在程序运行时能对K文件(求解文件)进行某些小程度改动的一种分析。通过它可以更改结果文件输出时间间隔,重新设置求解时间,删除某些接触和单元,更改某些速度、边界和荷载条件,进行刚体和变形体的转换,更改某些控制参数等。
(2) 完全重启动:对原来计算模型K文件(求解文件)进行大量修改时进行的一种分析。通过它可以增加新的材料和PART,增加新的接触定义,更改曲线、阻尼的定义和一些控制参数等。完全重启动可以说是一种全新的分析,只不过这种分析希望继承原来分析中相关PART的变形和应力情况,将其作为完全重启动时的初始条件。
本文运用小型重启动对碰撞体施加初始速度、删除某些单元等,使用完全重启动来对模型进行修改后对模型进行变形及应力的初始化,两种重启动交替使用,从而完成整个过程的模拟。吊杆断裂模拟的整个过程可以表示为图4所示过程。
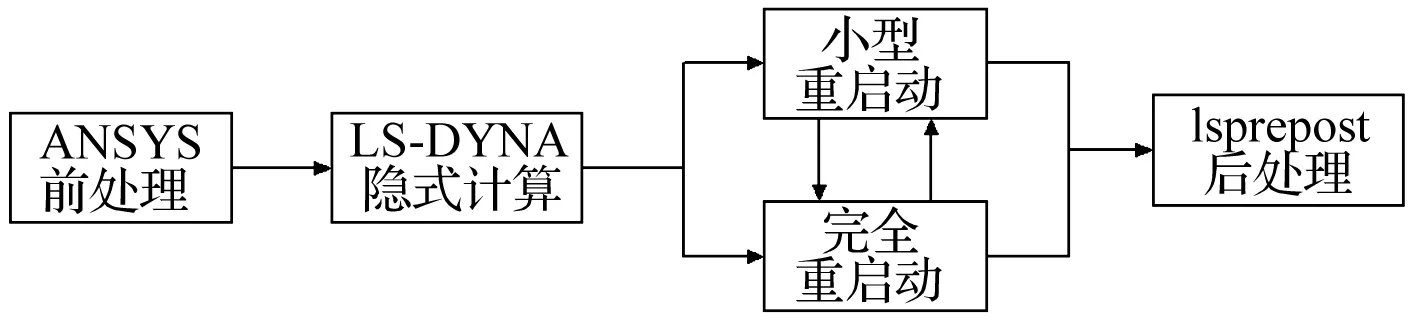
图4 吊杆断裂模拟过程
由于要考虑吊杆的断裂,模拟吊杆的本构模型采用ANSYS/LS-DYNA中的材料Material 3,采用Plastic Kinematic模型,如图5所示,该模型的基本公式为:
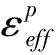
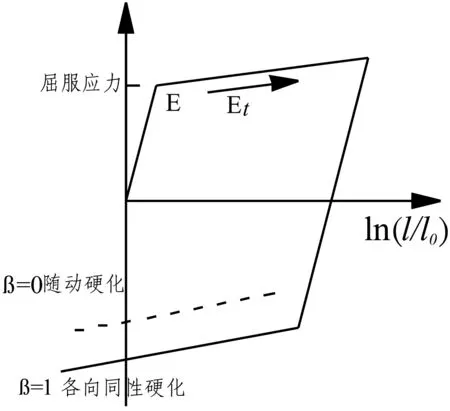
图5 Plastic Kinematic模型本构关系
Plastic Kinematic模型可以设置失效应变来考虑构件是否失效退出工作。通过设置吊杆的失效应变,可以使吊杆力达到一定值时吊杆即发生破断,从而产生相应的断索冲击的效果。吊杆受到碰撞时,相应的吊杆力时程曲线见图6。
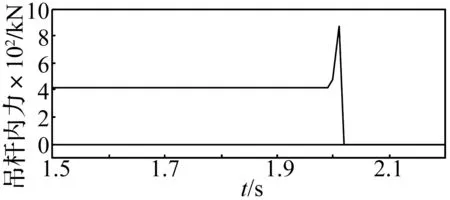
图6 受碰撞的吊杆力时程曲线
在动力分析中,塑性阻尼矩阵按Rayleigh阻尼矩阵考虑,阻尼比均取为0.05。
2.2 断裂吊杆的选取
在恒载作用下,长吊杆和短吊杆的受力情形是一样的,但短吊杆处于悬吊桥面与支承桥面交接处附近,该处集中了拱肋的受力变位和受温度作用的变位,以及桥道系温度变化时的变位,使得短吊杆比长吊杆更为不利。因此,本文重点对短吊杆断裂工况进行了分析讨论。
通过对不同荷载组合下该桥各吊杆力进行计算,根据最不利受力情况来确定吊杆断裂对象。根据最不利荷载基本组合(1.2恒载+1.4挂车荷载)进行承载能力极限状态分析,得到的各吊杆力分布示于图7(由于结构的对称性,仅列出单侧17根吊杆)。可以看出,3#和4#吊杆的吊杆力最大,故选取双短吊杆(3#和4#吊杆)作为短吊杆断裂的研究对象。
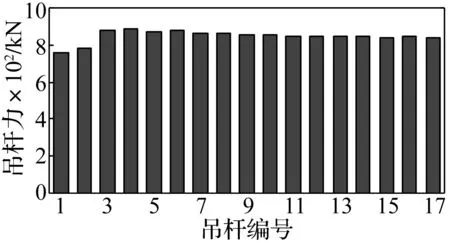
图7 最不利荷载基本组合下吊杆力
同时,为了考察长吊杆断裂时拱桥受力情况的变化,选取跨中附近且吊杆力相对较大的13#和14#吊杆作为长吊杆断裂的研究对象。
3 短吊杆断裂时全桥受力状态
3.1 吊杆
当短吊杆(3#和4#)断裂过程中,其余吊杆的轴力时程曲线分析可以得到,与3#和4#吊杆相邻的1#、2#吊杆和5#、6#吊杆的轴力变化最明显。图8给出了1#、2#、5#和6#吊杆力时程曲线。在3#、4#吊杆断裂冲击作用下,1#吊杆力最大为1421 kN,2#吊杆力最大为1546kN,均发生在吊杆断裂后约0.13 s;5#吊杆力最大为1225 kN,6#吊杆力最大为1 143 kN,均发生在吊杆断裂后约0.11 s。由于3#和4#吊杆断裂,与3#和4#吊杆相邻的左右吊杆的轴力变化量为初始轴力的3倍以上,因此需要考虑由于吊杆断裂过程中产生的大于静力响应的动力作用。
同时,与3#、4#吊杆横桥向对称的D3#、D4#吊杆处的桥面也因为断索冲击的作用而发生了较大的位移,D3#、D4#吊杆轴力最大值达到900 kN,且由于断索冲击作用产生的拱肋和桥面的振动向远处传播,使得离断裂吊杆较远处的吊杆轴力也发生了一定的变化,但变化量较小,最大轴力均小于700 kN。
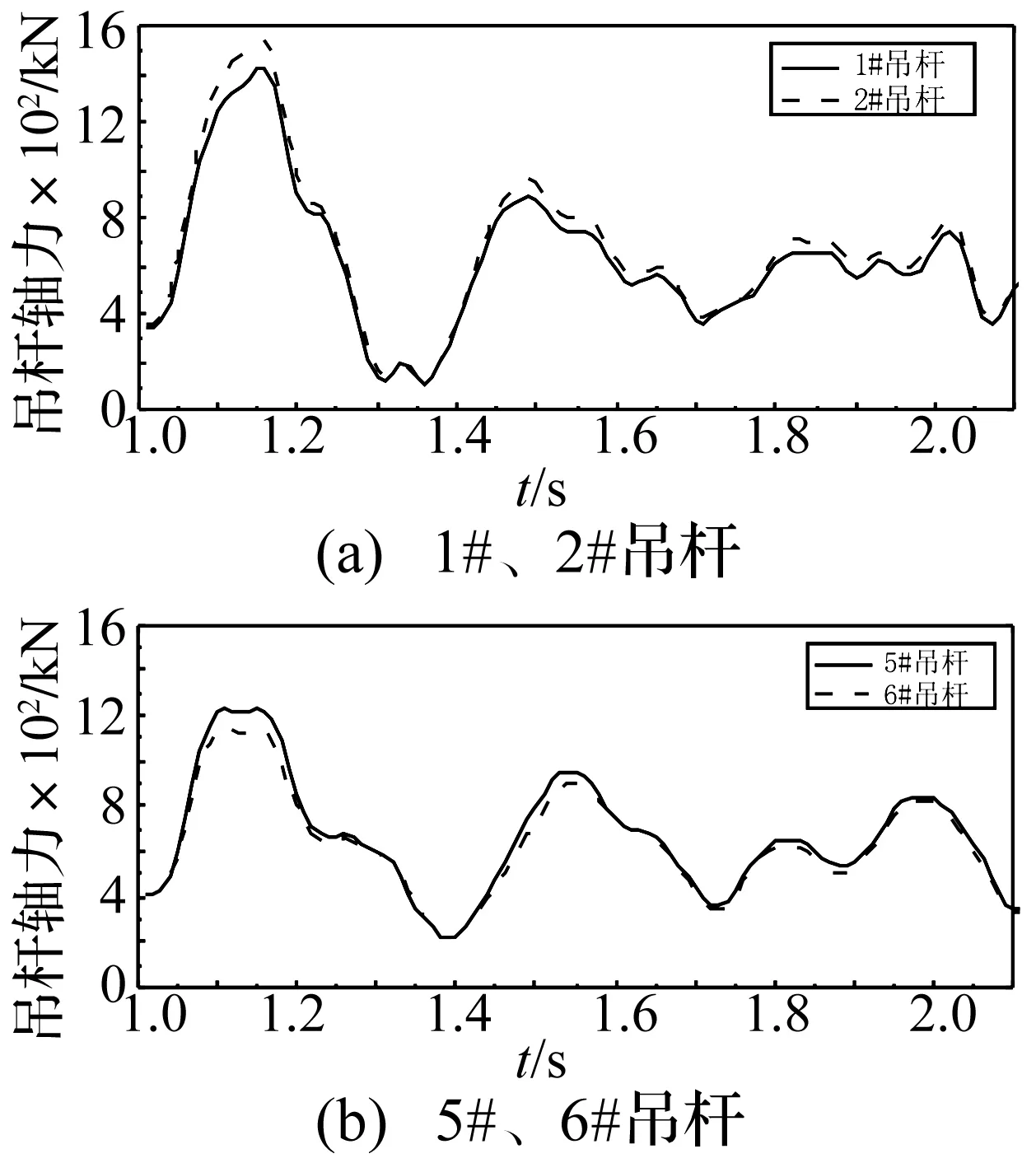
图8 双短吊杆断裂时相邻吊杆轴力时程曲线

图9 短吊杆断裂时断裂吊杆处拱肋和主梁的位移时程曲线
3.2 钢管混凝土拱肋
当短吊杆(3#和4#吊杆)断裂时,相应吊点处的拱肋和主梁位移时程曲线示于图9。可以看出,短吊杆断裂时拱肋位移变化较小,而主梁位移变化十分大,因此,短吊杆断裂对主梁产生的影响远大于拱肋。
以断裂吊杆吊点处达到最大位移为准,考察上下游侧拱肋拱脚截面、L/4截面和跨中截面拱肋内力变化情况。图10给出了吊杆断裂侧拱肋L/4截面弦杆内力时程曲线。在断裂吊杆吊点处位移达到最大时(t=1.08 s),拱肋截面轴力略有增大,弯矩未发生变化。L/4截面处上弦杆先减小后增大,下弦杆先增大后减小,上下弦杆弯矩变化规律相同。跨中拱肋在断索冲击作用下内力变化趋势一样。
短吊杆断裂前后拱肋内力变化见表3。可以看出,拱肋内力变化较小,通过拱肋承载力分析可知吊杆断裂后拱肋各截面均不会超过截面承载力。
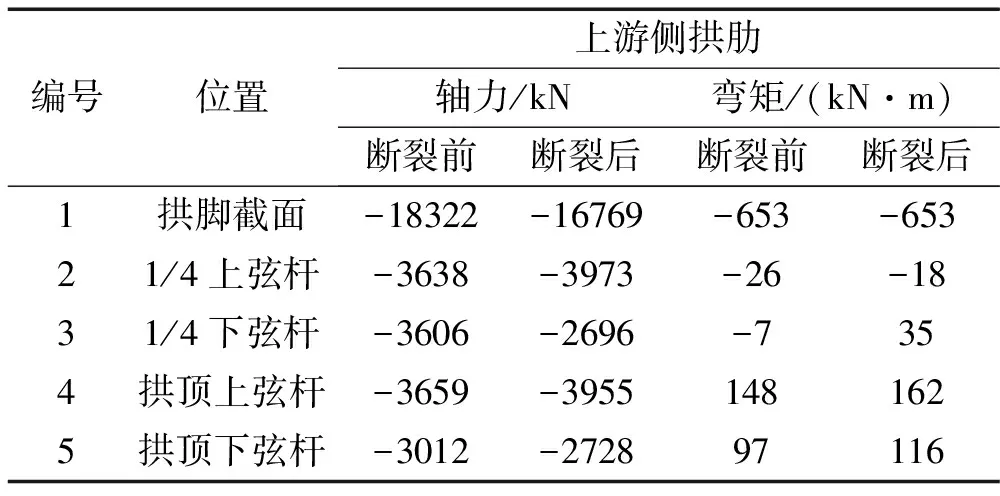
表3 短吊杆断裂前后拱肋内力
3.3 桥道系
该桥桥道系的纵梁与横梁连接采用焊接,纵梁为Q345钢,顶板和底板厚10 mm,纵梁与横梁连接处采用一级焊缝。由于焊缝连接是钢结构中的薄弱环节,本文主要考察吊杆断裂时纵梁处焊缝的内力变化情况。焊缝编号见图11。
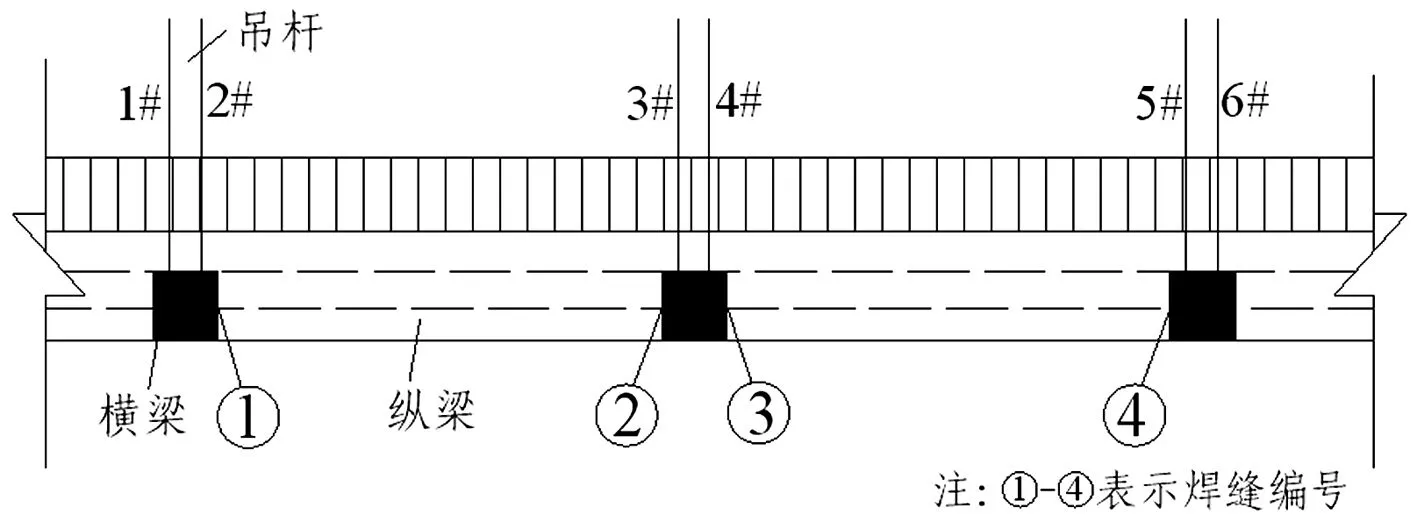
图11 纵梁焊缝编号示意图
图12为3#、4#吊杆断裂后②、 ③焊缝处弯矩和剪力时程曲线。可以看出,在断索冲击力作用下,②、 ③焊缝处弯矩和剪力突然剧烈增加,②处弯矩和剪力达3 204 kN.m和1 500 kN,③处弯矩和剪力达3 118 kN.m和-1 500 kN。 ①、④焊缝在断索冲击作用下内力变化约为②、 ③焊缝处内力的一半,焊缝①处弯矩和剪力为1 823 kN.m和645 kN,焊缝④处弯矩和剪力为1 429 kN·m和554 kN。
根据《钢结构设计规范》(GB50017-2003)[15]确定焊缝的抗力,示于表4。可以看出,在短吊杆断裂后②、 ③焊缝应力已超过抗力值,即纵梁可能会因焊缝强度不足而发生破坏,导致横梁及桥面板可能发生较大的竖向位移,使桥面板出现局部坍塌。
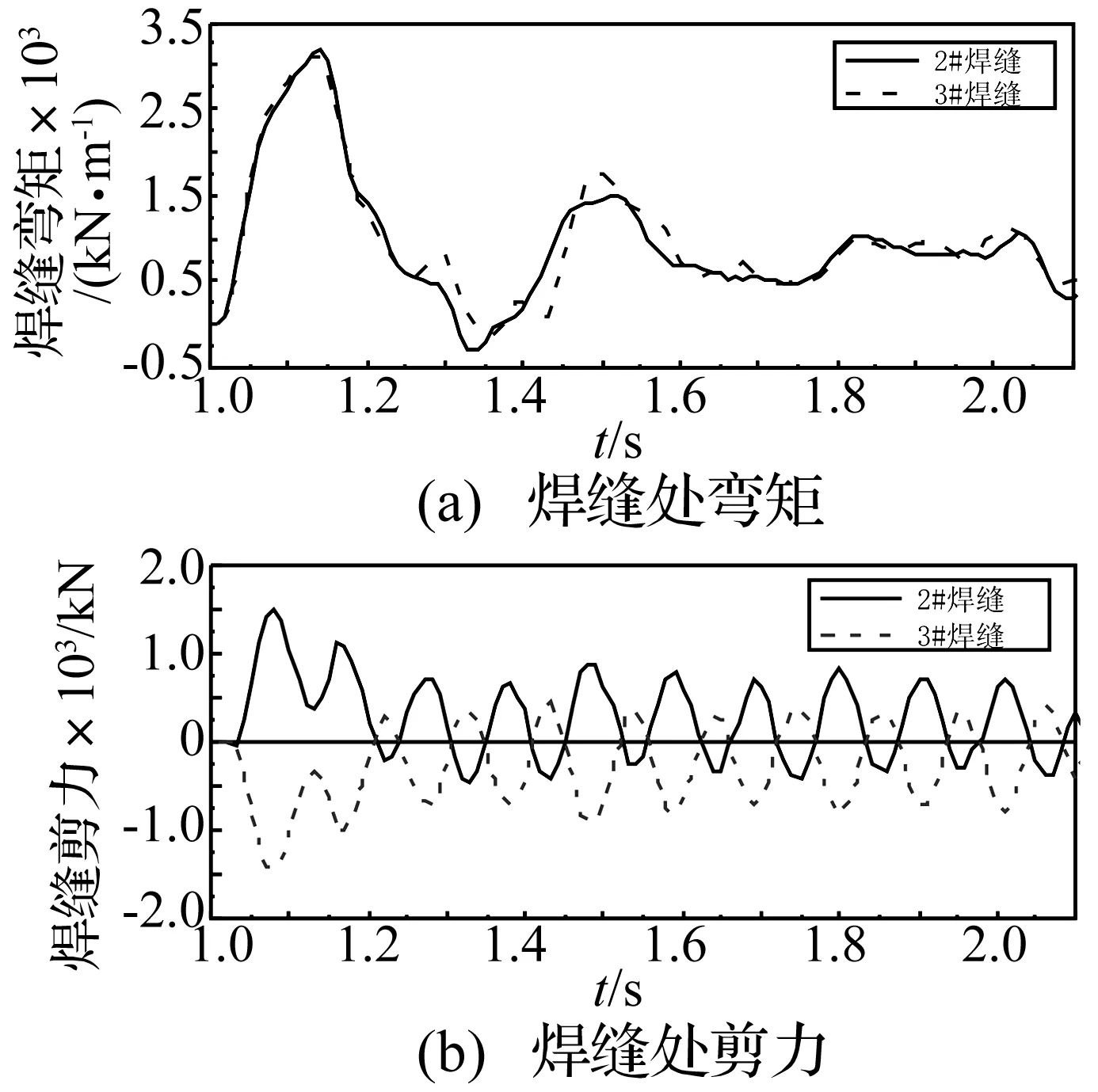
图12 短吊杆断裂时纵梁在②、③焊缝处的内力时程曲线

表4 短吊杆断裂时①~④焊缝应力和抗力
3.4 破坏形态
从前面的分析可知,在双短吊杆断裂后其他吊杆轴力均未超过容许值,不会发生破坏;拱肋内力变化较小,吊杆断裂后拱肋各截面承载力均满足要求;吊杆断裂处横梁两侧与纵梁连接处有可能因焊缝强度不足发生破坏,导致横梁及桥面板可能发生较大的竖向位移。因此,可能出现的破坏形态如图13所示,即桥道系出现局部坍塌的现象。
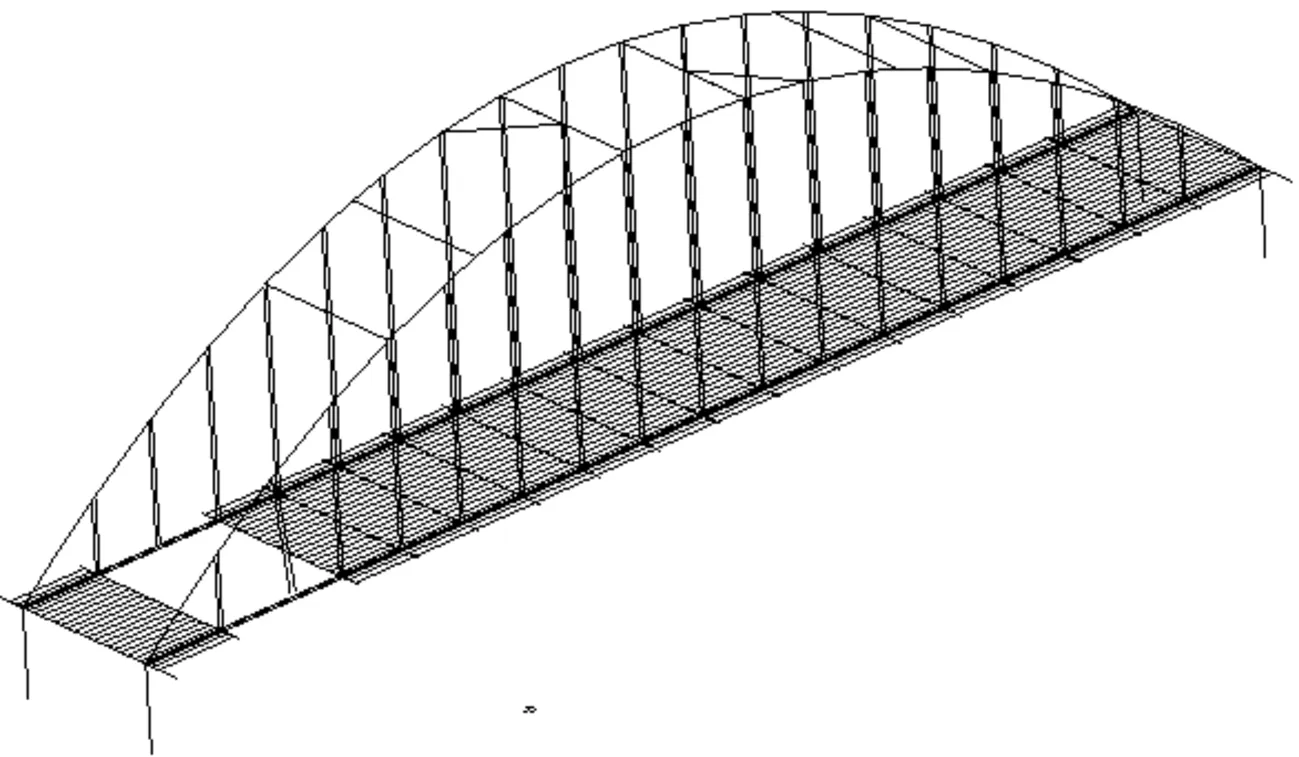
图13 短吊杆断裂时拱桥破坏形态
4 长吊杆断裂时全桥受力状态
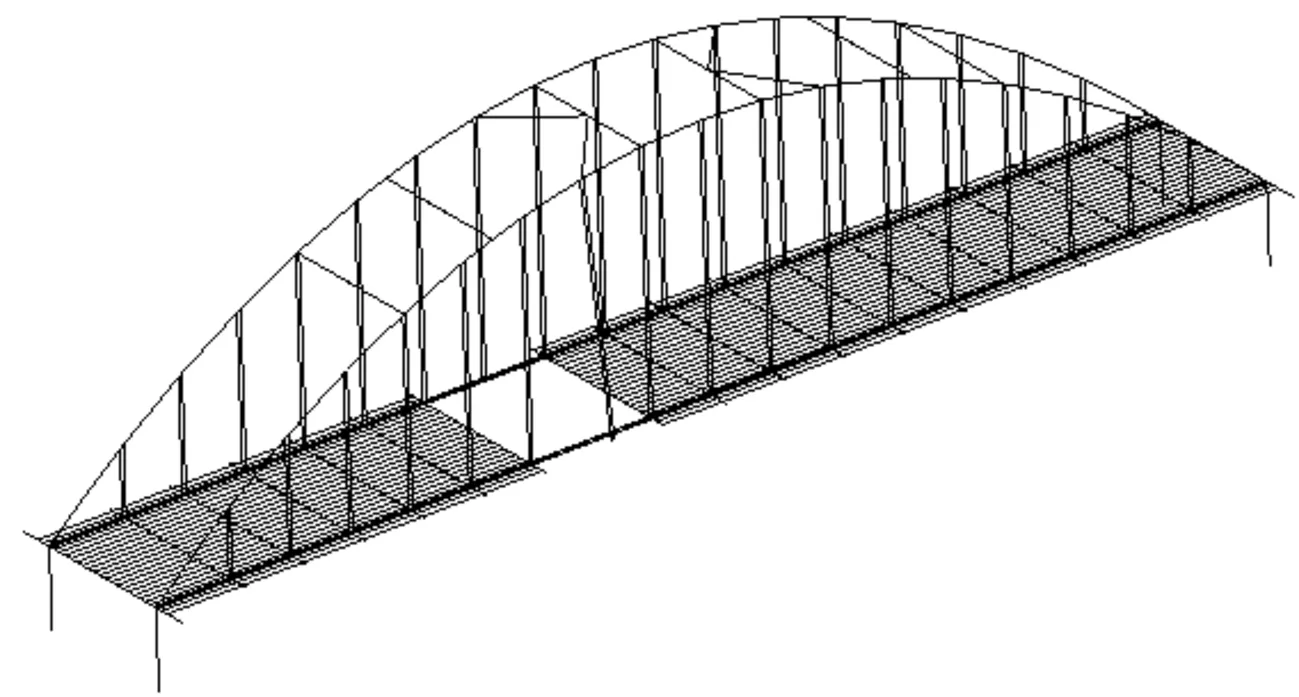
图14 长吊杆断裂时拱桥破坏形态
通过同样的计算方法对长吊杆断裂时全桥受力状态进行了分析,结果表明,在长吊杆断裂后桥梁结构破坏形态与短吊杆断裂后的破坏形态类似。其他吊杆和拱肋均不会发生破坏,吊杆断裂处横梁两侧与纵梁连接处有可能因焊缝强度不足发生破坏,导致横梁及桥面板可能发生较大的竖向位移而发生桥道系局部坍塌。因此,在13#、14#吊杆断裂后,拱桥可能的破坏情况如图14所示。
5 结 论
采用ANSYS/LS-DYNA建立一座下承式钢管混凝土刚架系杆拱桥的有限元模型,通过与实桥静动载试验进行的比较验证了建立的计算模型的正确性。
通过接触碰撞的方式进行吊杆断裂的模拟,分别选取最不利的同一截面双吊杆3#、4#两根短吊杆和跨中位置附近且内力相对较大的13#、14#两根长吊杆,进行了吊杆断裂前后全桥动力分析。分析结果表明,与断裂吊杆相邻的吊杆受到断索冲击的作用最大,其轴力变化量为初始轴力的3倍以上,需要考虑由于吊杆断裂过程中产生的大于静力响应的动力作用;吊杆断裂对主梁产生的影响远大于拱肋,拱肋内力变化较小;由于横梁两侧与纵梁连接处焊缝强度不足发生破坏可能导致桥道系局部坍塌。
本文研究了吊杆断裂的模拟算法及吊杆断裂引起的结构动力响应,为钢管混凝土拱桥安全可靠性设计提供了参考依据。如何将吊杆断裂时的动力效应简化为静力计算方式,如何通过桥梁结构构造设计提高结构抗连续性倒塌的能力有待进一步研究。
[1]陈宝春. 钢管混凝土拱桥(第二版)[M]. 北京:人民交通出版社,2007.
[2]郭志良. 拱桥吊杆断裂过程分析及对策研究[D]. 福州:福州大学硕士论文,2010.
[3]张秀成. 浅析“宜宾市小南门金沙江大桥”桥塌原因与修缮方案[J]. 河南城建高等专科学校学报,2002,11(2):15-17.
ZHANG Xiu-cheng. Analying the reason and renovating project of “little south door Jinsha River bridge of Yibin City”collapsing[J]. Journal of Henan Urban Construction Junior College. 2002, 11(2): 15-17.
[4]网易新闻. 新疆库尔勒孔雀河大桥部分垮塌[EB/OL]. http://news.163.com/photoview/00AN0001/14026.html/, 2011.
[5]百度百科. 武夷山公馆大桥[EB/OL]. http://baike.baidu.com/view/6108695.htm/, 2011.
[6]British Standard Institute. Structural Use of Concrete:(Part 1): Code of Practice for Design and Construction[S]. 1997.
[7]European committee for standardization. Euro code 1:Actions on Structures[S]. 2002.
[8]General Service Administration (GSA).Progressive Collapse Analysis and Design Guidelines for New Federal Office Buildings and Major Modernization Projects[S]. 2008.
[9]Department of Defense. Design of Buildings to Resist Progressive Collapse[S]. 2005.
[10]JTG D65-01-2007,《公路斜拉桥设计细则》[S].
[11]何晓晖,刘冰,李勇. 深圳北站大桥设计及施工简介[J]. 华东公路,2001,(06):28-31.
[12]韦建刚, 陈宝春. 钢管混凝土拱材料非线性有限元分析方法[J]. 福州大学学报(自然科学版),2004,32(3):344-348.
WEI Jian-gang, CHEN Bao-chun. Finite element methods for analysis on material nonlinearity of concrete-filled steel tubular arch[J]. Journal of Fuzhou University (Natural Science), 2004, 32(3): 344-348.
[13]蔡建国,王蜂岚,冯健,等. 大跨空间结构连续倒塌分析若干问题探讨[J]. 工程力学,2012,29(3):143-149.
CAI Jian-guo, Wang Feng-lan, Feng Jian, et al. Discussion on theprogressive collapse analysis of long-span space structures[J]. Engineering mechanics, 2012, 29(3):143-149.
[14]Wolff M, Starossek U. Cable-loss analyses and collapse behavior of cable-stayed bridges[C]. IABMAS2010, The Fifth International Conference on Bridge Maintenance, Safety and Management, July 11-15, 2010, Philadelphia, USA.
[15]GB50017-2003,钢结构设计规范[S].

