一种求解简支钢—混结合梁通用挠度表达式的数学解析方法
侯忠明,夏 禾,王元清,张彦玲
(1. 清华大学 土木工程系,北京 100084;2. 北京交通大学 土木建筑工程学院,北京市 100044; 3. 石家庄铁道大学 土木工程学院,石家庄 050043)
钢-混结合梁(下文简称结合梁)充分利用混凝土板抗压和钢梁抗拉的特点,采用抗剪连接件连接。这种构造方式受力性能优越,造型多样且施工方便,被大量应用在建筑、公路和铁路桥梁中。对于短跨及中等跨度的桥梁,尤其是60 m至80 m范围内,钢-混凝土结合梁桥的单位面积造价比混凝土桥要低18%以上,在综合效益上具有一定的优势[1],欧美等国在25 m~60 m跨径范围内的桥梁几乎都采用结合梁[2]。
由于抗剪连接件的柔性,外荷载作用下混凝土板和钢梁之间会产生一定的滑移,因此在进行结合梁静力计算时,必须要考虑由于这种滑移带来的影响[3]。而正是由于界面滑移的存在,与普通的单一材料梁(如混凝土梁,钢梁等)相比,其动力特性也表现出显著不同[4-5]。
当前公开报道的考虑界面滑移的结合梁挠度的表达式方法一般有以下几类:
第一类方法是基于弹性理论的换算截面法,也是最早期的方法,首先由Andrews[6]提出,假定钢与混凝土两种材料均是理想的弹性体,两者完全连接,变形协调,通过弹性模量比将混凝土换算成钢材,按材料力学的方法进行计算。但这种方法未考虑钢与混凝土交界面上实际的相对滑移,使承载力及变形结果偏于不安全,应该说,弹性设计法只适用于正常使用极限状态的分析。
第二类方法是为避免第一类方法带来计算误差,以刚度折减系数[7]或组合系数[8]的形式建立了结合梁的刚度计算公式,来考虑滑移对结合梁整体刚度降低的影响,计算接结合梁的挠度表达式。这两种方法虽然考虑了滑移因素,能体现组合梁实际变形性能,但刚度折减系数ξ的表达式并不是单调函数,受剪力连接件取值范围的限制;后者的组合系数方法是建立在半理论半经验的基础上,只有两个极端情况下放大系数ψ的解析解,中间取值只能用插值方法,且只能近似求得部分连接结合梁的挠度,未考虑完全连接时滑移效应的影响。
第三类方法是通过钢梁与混凝土板之间的相对滑移微分方程,考虑结合梁因滑移而引起的附加挠度,以得到考虑抗剪连接件柔性的结合梁挠度的一般公式[9]。这种方法考虑了滑移效应和剪力连接程度的影响,为了满足工程应用需要,采用了一些修正系数和构造限制以满足计算要求。
另外一种方法是通过能量变分原理,对混凝土翼板的内顶板、悬臂板和钢梁底板分设不同的纵向翘曲形函数,并考虑钢梁与混凝土板之间的相对滑移,采用概念比较明确的位移叠加法,得到不同荷载作用方式下结合梁挠度的解析解[10]。这种方法能够考虑结合梁剪切变形以及剪力滞的影响,能够求得多种荷载作用下结合梁的通用挠度表达式,但其中一些计算参数的计算方法较复杂。
上面几种考虑滑移的结合梁挠度的求解方法,均是基于静力理论。本文根据结合梁的基本动力理论(详细推导见文献[11]),基于模态叠加法,本文提出一种全新的求解集中荷载作用下结合梁的通用挠度表达式的数学分析方法,并与测试结果进行了对比。此方法的特点是:荷载可以是常量荷载,稍作变换也可以求得一定形式的时变荷载(如简谐荷载)作用下的挠度;同时,推导过程物理意义清晰,表达式参数意义明确,实际应用方便。本文以常量荷载为例,对所提出的方法进行说明。
1 基本分析模型及振动方程
为考虑抗剪连接件的影响,把结合梁划分成两个子梁,即混凝土板和钢梁,见图1。
建立基本分析模型时,作如下假设:
(1) 混凝土板和钢梁之间没有因掀起而脱离,即二者竖向变形协调;
(2) 考虑到一般的结合梁高跨比比较小,故忽略转动惯量和剪切变形的影响;
(3) 钢梁及混凝土板未发生大变形,均视为梁;
(4) 剪力栓钉承受的剪力沿梁长均匀分布,纵向单位长度的剪切刚度为常量;
(5) 在小变形时,栓钉所承受的剪力与变形成线性关系。
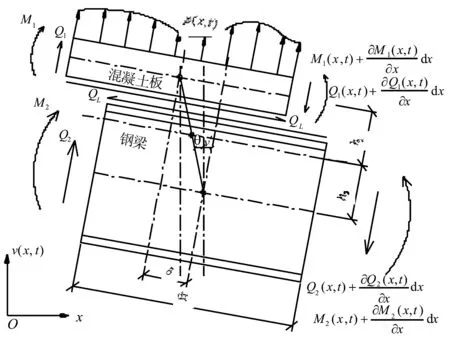
图1 结合梁微元示意图
1.1 微元平衡方程
取长度为dx的一段微元,其交界面上的剪力可表示为QL(x)=Ksδdx,并作以下定义:下标1、2分别代表混凝土和钢梁。
(1) 竖向力平衡方程
假设混凝土板与钢梁的阻尼系数分别为c1(x)和c2(x),分别考虑钢梁与混凝土板微元的竖向力平衡,即可建立结合梁微元的竖向力平衡方程
(1)
式中:Q(x,t)、m(x)和c(x)分别为单位长度的梁所承受的剪力、质量和阻尼系数。
(2) 弯矩平衡方程
假设混凝土板和钢梁重心轴之间的距离为h,它们到整个结合梁的重心轴的距离分别为h1和h2,显然h=h1+h2。对两个子梁的重心轴右侧分别取矩并求和,则可得到结合梁微元的弯矩平衡方程
(2)
式中:M(x,t)、Q(x,t)、f1(x,t)和fD(x,t)分别为梁体所承受的弯矩、剪力、惯性力和阻尼力。
(3) 位移协调方程
假设在dx的长度范围内,当梁体发生竖向挠度v(x,t)时,所引起的混凝土板与钢梁之间的纵向相对滑移为δ,由此而引起的重心轴法向连线的转角为θ,混凝土板和钢梁的转角为v′,则由图1可知
δ=(θ+v′)h
(3)
若不考虑式(2)中的极小项,则其可写为
(4)
显然,对于长度为dx的微元,有以下关系式
Ksh2(θ+v′)=(EI)cθ″
(5)
式中:θ为由混凝土板和钢梁之间的相对滑移引起的其重心轴法向连线的转角。上式左端为长度为dx的结合梁的滑移δ引起的弯矩,而右侧为长度为dx结合梁滑移角θ引起的弯矩。
1.2 振动方程的建立
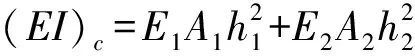
p(x,t)+Ksh2(θ′+v″)
(6)
由式(6)和式(5)整理可得考虑了结合梁滑移的等截面直线结合梁的运动方程
(7)
式(7)中:(EI)F=(EI)C+(EI)B,表示抗剪连接件的刚度KS为无穷大时结合梁的截面刚度,即相当于二者之间没有滑移的状态。
2 结合梁振动方程的求解
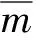
2.1 振动方程的求解及振型方程
假定解的形式为
v(x,t)=φ(x)·q(t)
(8)
式中:φ(x)表示振型,可看作式(7)的特征函数,而q(t)表示随时间变化的振幅。代入式(7),可得分离变量后的结合梁的振动方程,即
(9)
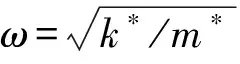
(10)
为6阶常微分方程,其特征方程为
(11)
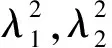
φ(x)=Asinhλ1x+Bcoshλ1x+Csinhλ2x+
Dcoshλ2x+Esinλ3x+Fcosλ3x
(12)
这就是等截面简支直线结合梁的振型方程。根据不同的边界条件,可得到各个系数的值。
2.2 边界条件和自振频率
对于等截面简支直线结合梁,在x=0及x=L处,梁的位移、弯矩均为0;θ′可视为其角滑移应变,在端部时为0,在跨中最大。那么根据式(5),有以下关系:
分别代入式(12),可得到关于系数A,B,C,…的六元齐次方程。若使上述六元齐次方程系数A,B,C,…不全为0,那么其系数矩阵行列式(6阶)的值应该为0,即
sinhλ1Lsinhλ2Lsinhλ3L=0
(14)
式(14)中仅当sinhλ3L=0时才成立,即λ3=nπL,则振型φn(x)=sin(nπL)。以λ=±iλ3代入式(11)可得
(15)
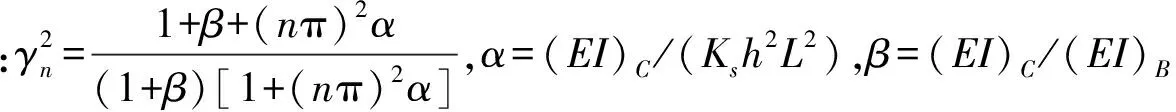

(16)
形式上与普通直梁一致,而(EI)F可视为不考虑滑移时结合梁的刚度。那么有
ωn=γnωn,F
(17)
(18)
式(18)中:(EI)eq表示结合梁的等效刚度。

3 集中荷载作用下简支结合梁的振动
3.1 振动方程的建立
在前文推导的基础上,把各阶振型分量叠加起来,于是有
(19)
式(19)两边各乘以φn(x),并沿梁长对x积分,有

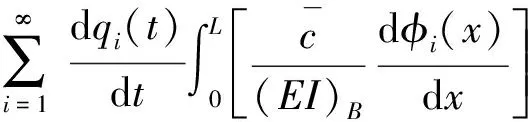

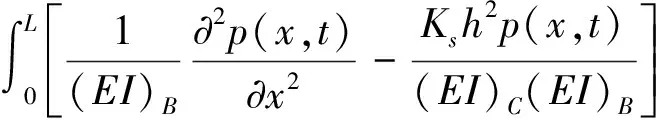
(20)
利用简支直线结合梁的正交条件及相应的边界条件[11],可知当i≠n时,其运动方程的某些项等于0,而广义阻尼项也可以简化。则上式可写成
(21)
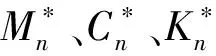

(22)
3.2 集中荷载下的振动方程
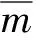
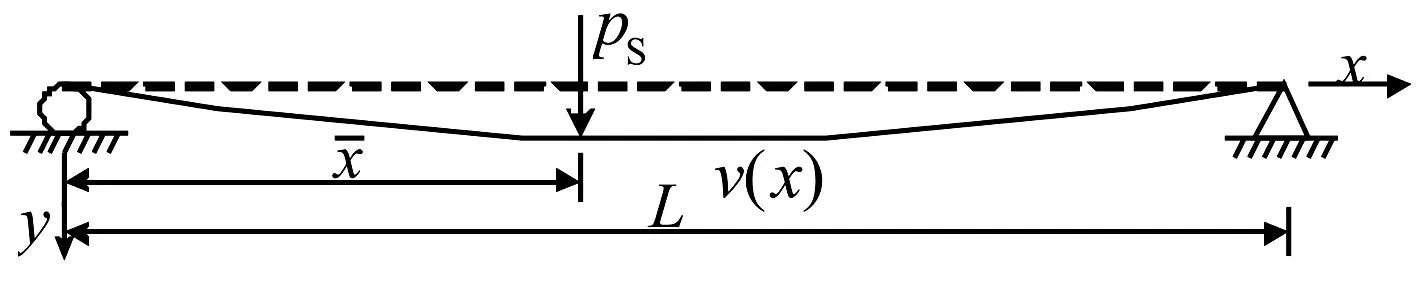
图2 集中力作用下结合梁的响应
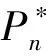
(23a)
(23b)
(23c)
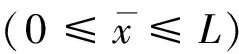
(23d)
(24)
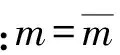
上式为常系数线性微分方程,各阶振型方程是相互独立的。虽然上述方程表达式与普通梁没有差别,但其自振圆频率表达式却比普通梁的复杂得多,见式(15)。注意到,此处荷载ps不随时间而改变,从形式上看,式(24)的结果反映了施加集中荷载后结合梁的最终反应。
3.3 振动方程的求解
式(24)为常系数线性微分方程,若忽略瞬态项,容易得到其特解为
(25)
上式中,由于ps为不随时间改变的常力,因此表达式中右侧项同样没有出现时间项。
由前文推导可知,简支结合梁的第n阶振型可表示为φn(x)=sin(nπx/L),那么根据振型叠加法,承受集中荷载的结合梁的最终反应为
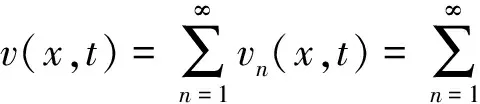
(26)
式中,v(x,t)为梁上x位置时的挠度值。
把结合梁自振圆频率的表达式代入,并作三角函数变换,有
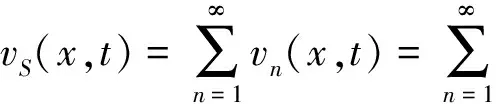
vS1+vS2+vS3
(27)
式中:
上式中的级数有三项,包含数学中的常用的两种级数形式,即
(28a)
(28b)
vS1和vS2可转化为S1所示的级数形式,S1的求和结果为[12]

(0<θ<1)
(29)
式中:φn(x)为Bernoulli函数,Bk为Bernoulli数。
vS3可转化为S2所示的级数形式,S2求和结果为
(30)
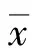
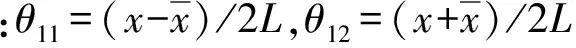
当k=1时,φ2(x)=x2-x,B1=1/6;当k=2时,φ4(x)=x4-2x3+x2,B2=1/30。把上述表达式代入式(27)并简化,有
(31a)
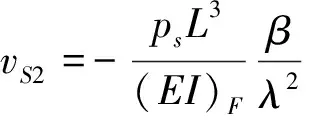
(31b)
其中
把a2=(1+β)/(απ2)=(λ/π)2代入并稍作变换,得到vS3具体结果为
(32)
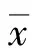
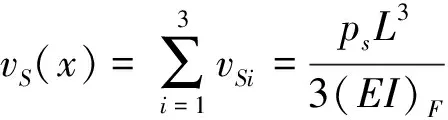
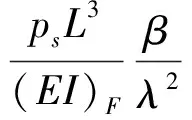
(33)
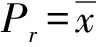
(34)
可知,当知道集中荷载在梁上的作用相对位置后,通过上式容易求出结合梁的任意位置处的竖向挠度,且这个挠度不随时间变化。

(35)
上述表达式共有两项:第一项相当于不考虑结合梁的滑移时的挠度表达式,与普通梁的一致;第二项是考虑滑移后的附加挠度。第一项和第二项之和,就是结合梁在集中静荷载作用下的挠度表达式。
上述推导均未考虑剪切变形和剪力滞的影响。下文将结果的正确性进行验证。
4 推导结果验证
4.1 理论验证
(1) 与现有公式的比较
对于式(33)和式(34)中第一项,相当于不考虑滑移的普通梁,经过简单变换,结果与结构力学里的结果完全一致,即按初等梁理论得到的结果。之所以分成两个表达式,是因为集中力的存在导致剪力分布图的突变,其表达式为分段函数。
如果同时考虑滑移的影响,式(33)和式(34)和文献[10]中公式(2-52)和(2-53)的表达式一致(不考虑剪切变形和剪力滞的影响)。这说明本文从动力理论所得到的集中荷载作用下结合梁挠度的静力表达式是正确的,验证了推导结果的正确性,换算过程略。
假如集中力ps作用在跨中,那么Pr=Px=0.5。代入式(33)和式(34),经过变换得到
(36)
与文献[5]中的表达式完全一致,且前一项与普通梁在同样荷载作用下的挠度表达式一致。
可以看出,对结合梁力学行为的求解,有多种方法和途径,从动力学方法所得到的结果,同时也反映了结合梁的动力学和静力学之间的联系。从某种意义上来说,静力荷载作用于结合梁上时,是其动力响应的一种特殊状态。
4.2 试验验证
(1) 模型参数
采用作者在文献[11]中的简支钢-混结合梁模型。模型为箱型截面,跨度4 200 mm,梁全长4 500 mm,混凝土板长4 400 mm,宽700 mm,厚110 mm;钢梁高200 mm,下翼缘宽500 mm,翼缘板厚8 mm,腹板厚6 mm;栓钉直径13 mm,高50 mm。每片梁用Q235钢材430 kg,C30混凝土0.35 m3,栓钉42个(部分连接PCB,剪力连接度为60%)或70个(完全连接FCB)。栓钉刚度的取值原则参见相关文献[13-14]。
(2) 结果验证

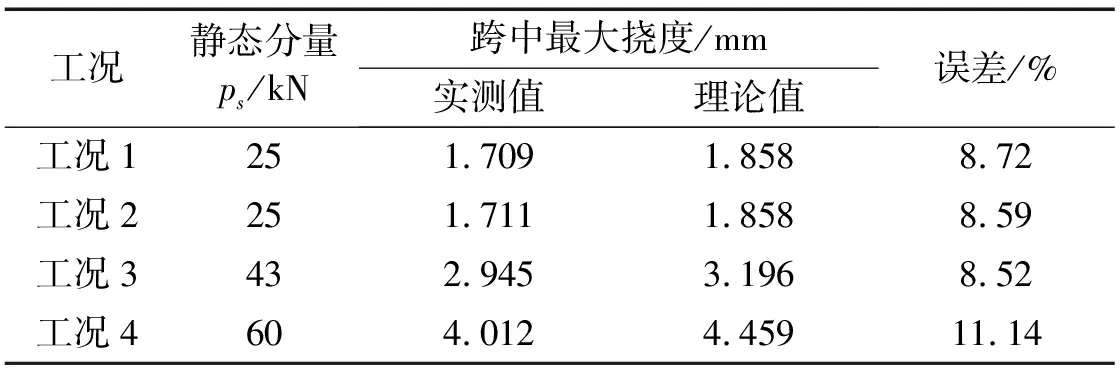
表1 集中荷载作用下简支结合梁的跨中挠度
从表中可以知道,对于此试验梁而言,在上述荷载大小的范围内,结合梁跨中挠度的理论值与实测值吻合良好,进一步验证了本文推导的正确性。
5 结 论
通过本文建立的结合梁基本动力理论,得到了集中荷载(也可以是其它形式的荷载)作用下结合梁静挠度的通用级数表达式,通过一定的数学变换,使其符合级数求和条件;将其相应的Bernoulli函数和Bernoulli数代入,即可得到与静力方法一致的集中荷载作用下结合梁挠度的通用表达式,且能体现滑移引起的附加挠度的影响。并与实测结果进行了对比,结果吻合良好。
主要结论如下:
(1) 与普通单一材料的梁相比,考虑相对滑移后的结合梁动力平衡方程形式上更为复杂,明显体现了抗剪连接件的影响,但仍可简化为常见的二阶常系数微分方程进行求解;
(2) 考虑钢梁与混凝土板之间的界面滑移后,结合梁的竖向自振频率明显降低。这说明界面相对滑移使结合梁整体刚度下降,频率降低,因此在静力和动力计算中都必须考虑其影响;
(3) 通过一定的数学变换,可将通常只能数值求解的响应表达式满足级数求和条件,以相应的Bernoulli函数和Bernoulli数代入,即可得到集中荷载作用下简支结合梁的通用挠度表达式,此表达式不仅能体现不考虑滑移的单一材料梁的挠度结果,也能反映因滑移引起的附加挠度的影响。
(4) 本文的方法不仅适用于结合梁,也适用于普通梁;荷载作用形式可以是常量荷载,稍作变换也可以求得一定形式的时变荷载(如简谐荷载)作用下的挠度;可以是单个荷载,也可以是多个荷载;同时,本文挠度表达式参数意义明确,应用方便。
[1]Taly N.Design of modern highway bridges [M]. McGraw-Hil1 Companies. Inc, New York, 1998.
[2]Theodore V. Galambos. Recent research and design developments in steel and composite steel-concrete structures in USA. Journal of Constructional Steel Research, 2000(55): 289-303.
[3]张晔芝. 高速铁路连续结合梁的响应分析 [J]. 铁道学报, 2002, 24(6): 84-88.
ZHANG Ye-zhi. Analysis on responses of continuous composite beams in high-speed railways [J]. Journal of the China Railway Society, 2002, 24(6): 84-88.
[4]蒋丽忠,丁发兴,余志武. 钢-混凝土连续组合铁路桥梁综合动力性能试验研究 [J]. 中国铁道科学. 2006, 27(5): 60-65.
JIANG Li-zhong, DING Fa-xing, YU Zhi-wu. Experimental study on the integrated dynamic behavior of continuous steel-concrete composite girders of railway bridges [J]. China Railway Science, 2006, 27(5): 60-65.
[5]Huang C W, Su Y H. Dynamic characteristics of partial composite beams [J]. International Journal of Structural Stability and Dynamics, 2008, 8(4): 665-685.
[6]Andrews E S. Elementary principles of reinforced concrete construction [J]. Scott, Greenwood and Sons, 1912.
[7]聂建国,李勇,余志武,等. 钢-混凝土组合梁刚度的研究 [J]. 清华大学学报(自然科学版), 1998, 38(10): 38-41.
NIE Jian-guo, LI Yong, YU Zhi-wu, et al. Study on short and long-term rigidity of composite steel-concrete beams [J]. Journal of Tsinghua University (Sci & Tech), 1998, 38(10): 38-41.
[8]王景全,吕志涛,刘钊. 部分剪力连接钢-混凝土组合梁变形计算的组合系数法 [J]. 东南大学学报(自然科学版), 2005, 35(Sup (I)): 5-10.
WANG Jing-quan, LÜ Zhi-tao, LIU Zhao. Consistency factor method for calculating deformation of composite steel-concrete girders with partial shear connection [J]. Journal of Southeast University(Natural Science Edition), 2005, 35(Sup (I)): 5-10.
[9]聂建国,沈聚敏,袁彦声. 钢-混凝土简支组合梁变形计算的一般公式 [J]. 工程力学, 1994, 11(1): 21-27.
NIE Jian-guo, SHEN Ju-min, YUAN Yan-sheng. A general formula for predicting the deflection of simply supported composite steel concrete beams with the consideration of slip effect [J]. Engineering Mechanics, 1994, 11(1): 21-27.
[10]张彦玲. 钢-混凝土组合梁负弯矩区受力性能及开裂控制的试验及理论研究 [D]. 北京:北京交通大学,2009:20-32.
[11]侯忠明,夏禾,张彦玲. 栓钉连接件抗剪刚度对钢-混凝土组合梁自振特性影响研究[J].中国铁道科学,2012,33(6):24-29.
HOU zhong-ming, XIA He, ZHANG Yan-ling. The influence of the shear stiffness of stue connectors on the natural vibration characteristics of steel-concrete composits beams[J]. China Railway Science,Y2012,33(6):24-29.
[12]Jolley L B W, CANTAB M A. M.I.E.E.. Summation of series (second revised version) [M]. Dover Publications, Inc. , New York, 2005:106, 138.
[13]Design of composite steel and concrete structures, Part 1.1: General rules and rules for buildings-General rules, EN 1994-1-1[S]. Eurocode 4, European Standard, 2007.
[14]Gattesco N. Analytical modeling of nonlinear behavior of composite beams with deformable connection [J]. Journal of Constructional Steel Research, 1999(52): 195-218.

