结构振动对风特性测试结果的影响研究

程怀宇, 王 浩, 肖士者, 郭 彤, 邓稳平

(东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 210096)

近年来，我国建成许多跨江渡海长大跨桥梁工程，其结构形式主要以悬索桥、斜拉桥为主，如苏通大桥、润扬大桥、马鞍山大桥等。对于这些大跨度缆索支承桥梁来说，随着跨径的增加，结构刚度减小，使得风荷载经常成为控制荷载。Tacoma悬索桥发生颤振风毁事故七十年后的今天，桥梁风致振动早已引起了各国桥梁工程师们的注意。随着桥梁风工程研究的不断深入，风环境及风致桥梁振动响应监测已经成为其中的热点课题之一[1-5]。因此，这些新建大跨桥梁均安装了包括风速仪和振动传感器在内的结构健康监测系统(SHMS)[5-7]，用以监测桥位处的风环境以及风、车辆等引起的桥梁振动。SHMS已成为一个研究桥梁风致振动的现场试验平台，近年来也有不少专家学者利用SHMS或者桥位现场实测对强/台风下的大桥风场特性进行了研究，如朱乐东教授等针对香港青马大桥进行了台风特性及结构同步风致振动实测研究[6]；陈政清教授等以湖南岳阳洞庭湖大桥为例，对大跨多塔斜拉桥结构斜拉索的风雨振进行了现场实测研究[3]。上述研究工作都是以现场实测风数据为基础的。

本课题组近年来参与了包括润扬大桥、苏通大桥等SHMS的建设，由于地处东部沿海台风多发区，这些SHMS每年均能实时记录下经过桥址区的各类强风。与此同时，鉴于SHMS中风速仪数量较少，且风速仪采样频率较低，课题组紧密追踪桥址区天气情况，每年台风期间均上桥进行补充实测。近年来开展的台风实测研究从2005年的麦莎、卡努开始，直至2011年的梅花、2012年的苏拉、达维，总计10余个台风[7-8]。大量的实测研究表明，台风作用下大跨缆索支承桥梁会发生明显的侧向、竖向和扭转振动，尤其以主梁、主缆、吊杆和拉索的振动响应最为明显。这就说明在结构风特性实测过程中，固定在结构上的风速仪自身也是随着桥梁振动不断往复运动的。有必要研究结构自身振动对风速仪测试数据可靠性的影响，但目前尚未见相关文献报道，这也正是本文研究工作的意义之所在。

1 实验介绍

本实验的目的是分析结构自身振动对风速仪所测数据的影响。为了模拟风速仪随结构自身振动的情况，将风速仪固定在振动台上，通过振动台来模拟安装在实际结构中的风速仪基底的振动。实验中振动台分别输入韦帕台风作用下润扬大桥主梁跨中横向振动信号(如图1)和白噪声(如图2)，所测风由风机匀速转动所输出。

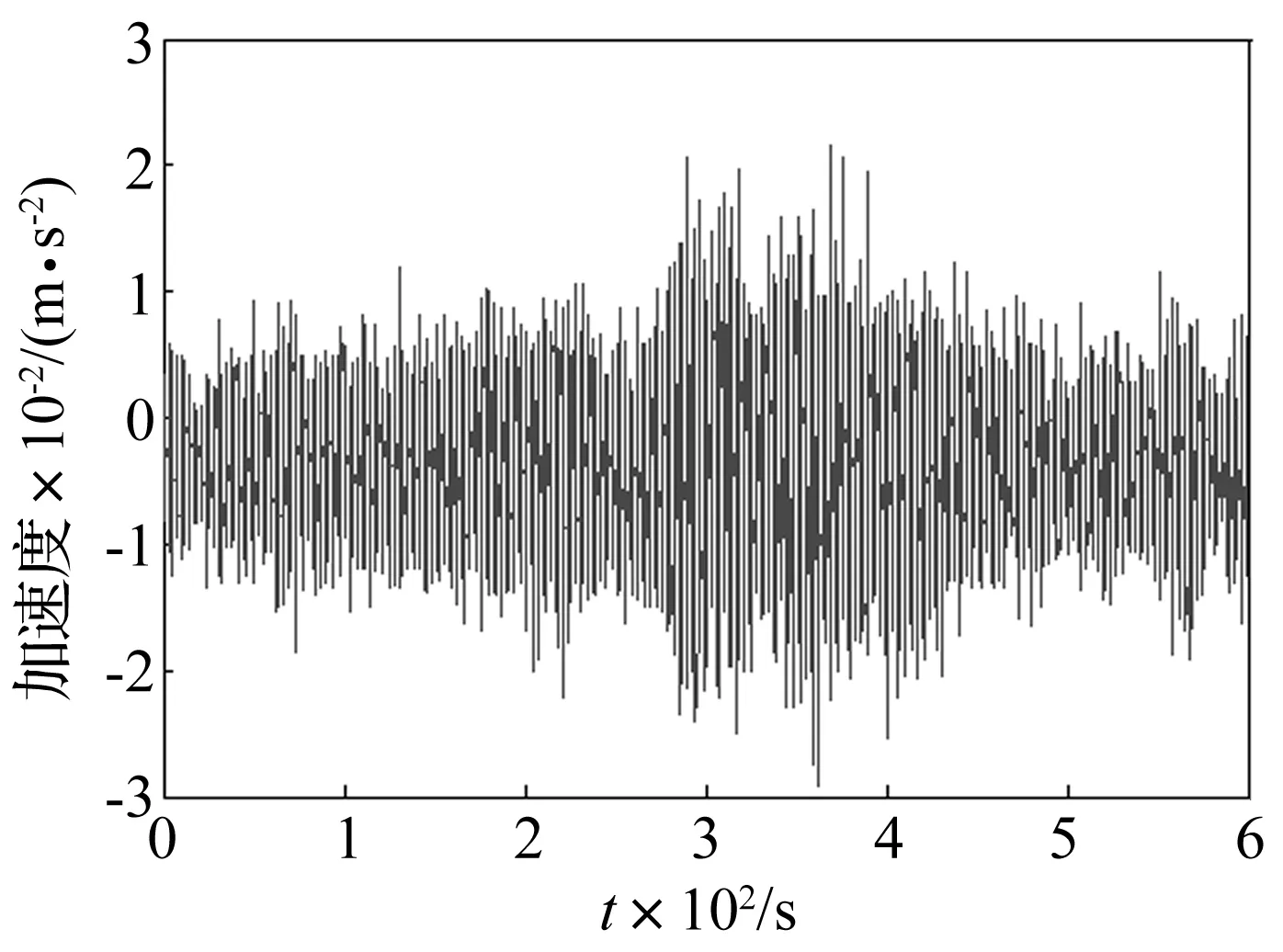
图1 主梁横向振动信号

图2 白噪声

实验在东南大学九龙湖校区土木交通实验室进行，所采用的两个风速仪分别是英国Gill仪器设备公司生产的WindMaster和WindMaster Pro三维超声风速仪，见图3(a)和(b)，测量精度设为0.01 m/s，采样频率均设为10 Hz，数据的输出方式选用了三维直角坐标方式。振动台为WS-Z30小型精密振动台系统，振动频率为20 Hz，如图3(c)所示。上述实验仪器、设备由专用UPS提供稳压电源。实验安排在实验室狭长走道中进行，以尽量模拟风洞环境、减小干扰。为了保证各有风速输入工况下来流风场的一致性，所采用的SF7-4型低噪声轴流风机在不同工况中均以相同的转速转动。本实验共设置了5种工况，为了对比验证实验数据的可靠性，每种工况均采用上述两台不同型号的风速仪分别进行数据采集。每个工况的数据采集均为时间10 min，具体实验工况的设置见表1。分析中以工况1与2的对比为主，其余工况主要作为对比和参考。

表1 实验工况

2 风速数据分析处理方法

为了便于分析研究，通常将随机的自然风V分解成不随时间变化的平均风U和随时间变化的零均值脉动风v。其中，平均风特性主要包括平均风速、攻角和风向等，表征脉动风的主要参数为紊流强度、紊流积分尺度和紊流功率谱密度函数等[9]。本文重点分析了结构自身振动对平均风速和紊流特性的影响，以评判振动给风场实测数据可靠性带来的影响。

2.1 平均风速

三维超声风速仪输出的三维风速数据[vx,vy,vz]分别为风速仪坐标系下各坐标方向的风速。为了方便分析研究，常采用风轴坐标系，风轴坐标系的u轴沿平均风U的方向，w轴与u轴垂直且与u轴共同构成竖平面，v轴与u、w轴垂直，u、v、w轴的正向构成一个右手坐标系[9]。通过坐标变换将实测风速数据[vx,vy,vz]转化到风轴坐标系下的风速[vu,vv,vw]，方法如下：

[vu,vv,vw]=[uvw]-1*[vx,vy,vz]

(1)

(2)

2.2 紊流强度

紊流强度是表征脉动风特性的主要指标之一，对结构风振响应有着重要影响。由于研究中通常将风场中任一点的瞬时物理量化为平均值与脉动值之和，并分别考虑。紊流强度是用来表征脉动值与平均值比值的量，它定义为风的脉动分量平均变化幅度(均方差)σu，σv，σw与平均风速U之比，顺风向、横风向和竖向紊流度分别用Iu，Iv，Iw表示，即：

(3)

2.3 紊流积分尺度

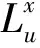
(4)

2.4 紊流功率谱密度

作为脉动风速的另一主要参数，紊流功率谱密度函数能够准确描述脉动风中各频率成分所作贡献的大小。以1948年Von-Karman提出的自由大气层的水平纵向脉动风速谱为例[10]：

(5)

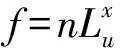
3 风特性分析结果的对比分析

3.1 对平均风速的影响

平均风速是在某段时间内的风速平均值，平均风速大小直接关系到风对结构作用的大小。本文取时距10 min计算平均风速，实验测得的顺风向风速时程曲线如图4所示，根据式(1)和式(2)算得各工况下的平均风速分别见表2。

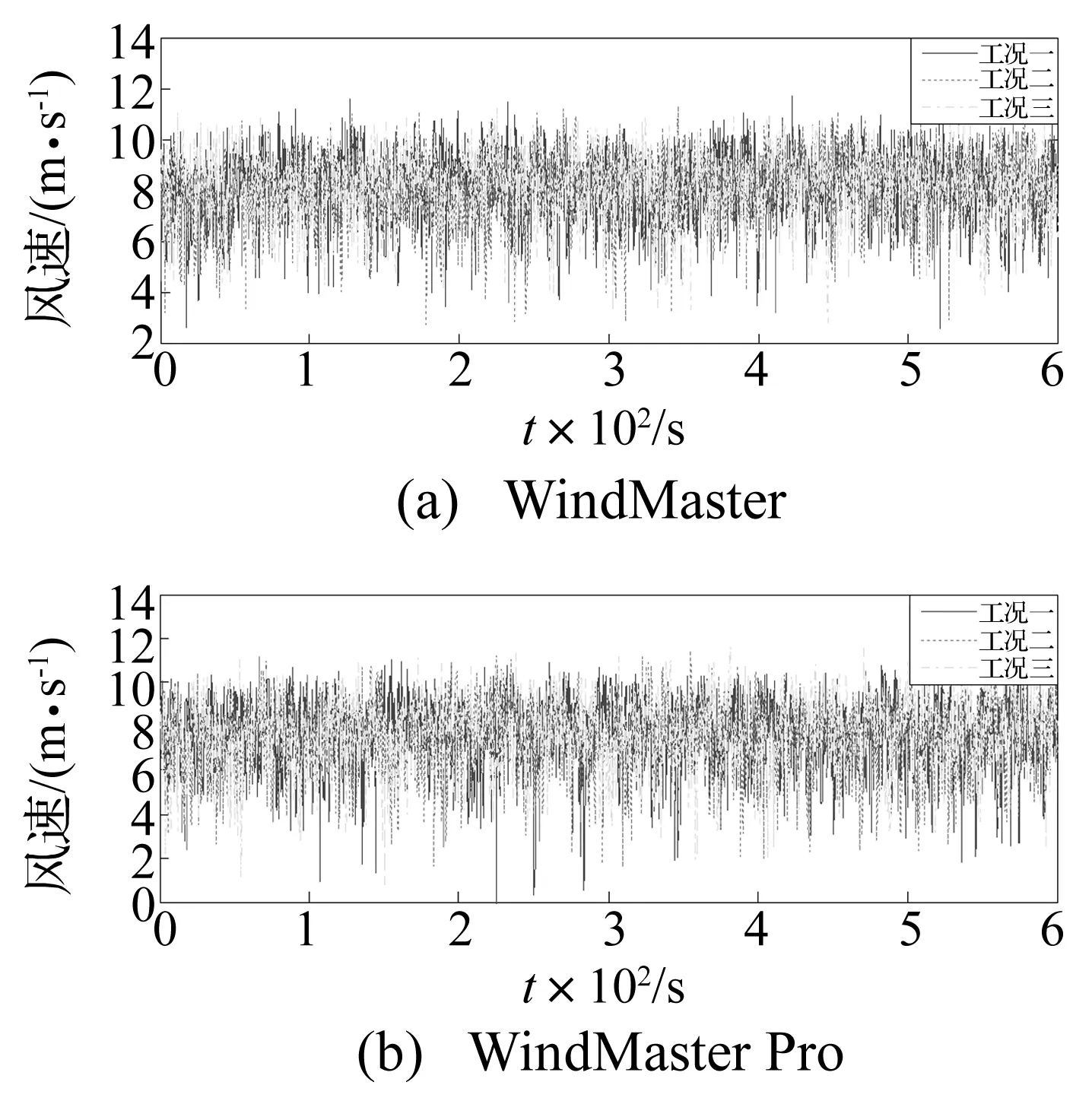
图4 实测风速时程曲线

表2 实测平均风速 (单位：m/s)

由表2可知，WindMaster风速仪在基底有无振动下所测平均风速差别较小，采用主梁振动和白噪声时的差别分别为1.83%和2.68%；WindMaster Pro风速仪在基底有无振动时的平均风速差别也较小，采用主梁振动和白噪声时分别为2.09%和0.26%。因此，结构自身振动对风速仪实测平均风速影响不大。

3.2 对紊流强度的影响

研究表明，在风速小于1.5m/s时，计算紊流强度已无意义[12]，因此，本文仅计算了1～3工况下的紊流强度。WindMaster和WindMaster Pro测得的紊流强度分别见表3和表4。

对比表3和表4可知：① 在振动台输入主梁振动信号下，风速仪基底的振动使两个风速仪测得的顺风向紊流强度都略变大，但增加幅度不明显，均在5%以内。这是由于三维超声风速仪测得的风速是相对风速仪自身的空气流动速度，而风速仪振动使空气和风速仪间产生了往复的相对运动，增加了风脉动分量的平均变化幅度。② 由于白噪声振幅较大，在采用白噪声输入时测得的顺风向紊流强度增大幅度较为明显。③ 横向和竖向紊流强度在主梁振动信号输入时有小幅增加，在白噪声输入时小幅减小。

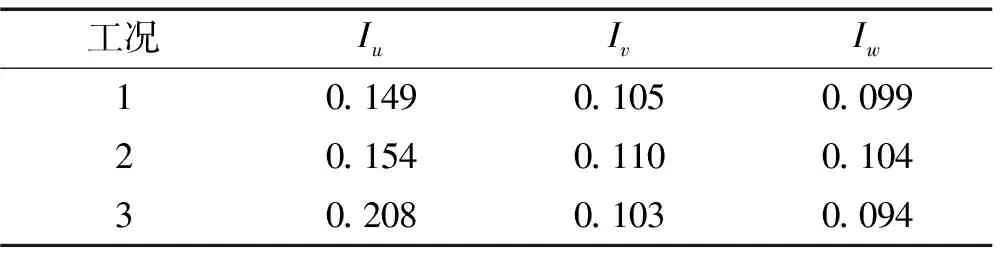
表3 WindMaster测得的紊流强度

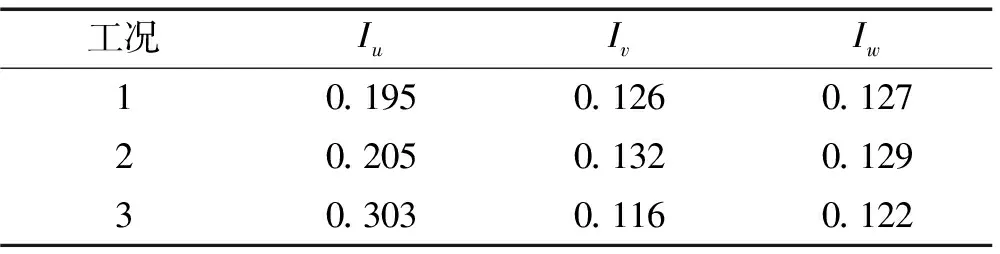
表4 WindMaster Pro测得的紊流强度

3.3 对紊流积分尺度的影响

紊流积分尺度的分析结果不仅取决于数据记录的长度和平稳程度，还取决于所采用的分析方法。因此，即使对于同一组数据，采用不同的分析方法也将得到不同的结果[10]。本文中紊流积分尺度均采用较为常用的式(4)求解，结果如表5和表6所示。

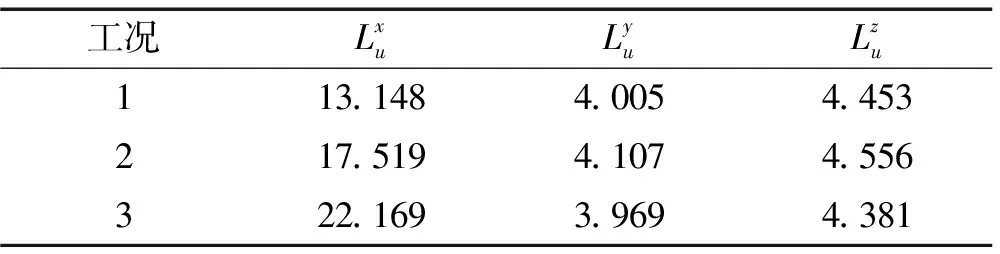
表5 WindMaster测得的紊流积分尺度

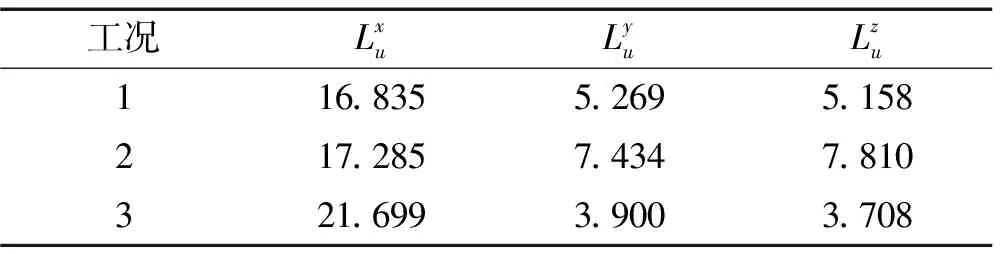
表6 WindMaster Pro测得的紊流积分尺度

由表5和表6可知：① 相比无振动情况，在振动台模拟主梁振动时顺风向的紊流积分尺度均有所增加，当白噪声输入时顺风向紊流积分尺度进一步增大。② 在基底振动台输入主梁振动信号和白噪声时，WindMaster测得的横向和竖向紊流积分尺度变化较小，而WindMaster Pro测得的横向和竖向紊流积分尺度变化较稳明显，但情况不一致。由于紊流积分尺度分析结果与所采用的分析方法直接相关，本次测试结果尚有待进一步验证。

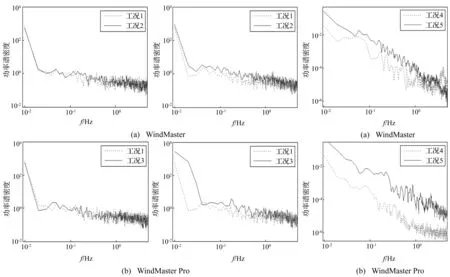
图5 实测顺风向风速功率谱密度

3.4 对风速功率谱密度的影响

实测风谱分析中，加了Hamming窗以减少由于时域信号截断而引起的频域信号泄漏。应用分段平滑技术以减少谱值的随机误差。10 min长的样本被分成28段，每段子样本长60 s(共600个数据)，相邻两个子样本重叠40 s(共400个数据)。每段数据被充零至2 048个，应用快速傅立叶变换(FFT)得到各种工况下的风速功率谱密度，如图5和图6所示。

图5(a)中WindMaster所测数据显示，工况2和3的风速功率谱密度与工况1差别很小，因此风速仪基底振动对风速功率谱密度的影响很小；图5(b)中WindMaster Pro所测数据显示，在小于0.5 Hz的相对低频部分，工况2和3的风速功率谱密度稍大于工况1，表明基底振动可能会导致所测风速功率密度的低频部分略高于实际情况。图5(a)和(b)以及图6的综合对比可知，基底振动会导致所测风速功率密度偏高，这种影响在低频部分尤为明显。

4 结 论

(1) 三维超声风速仪基底有无振动的各种工况下所测得的平均风速表明，基底振动对所测得的平均风速影响较小，试验中的最大差别在2.68%以内，对应基底采用白噪声输入下由Windmaster风速仪测得的情况。

(2) 实验结果表明，基底输入台风期间的主梁振动信号会使得风速仪实测得到的紊流强度值在三个方向均略有增加，但增加幅度不明显。就本次实验而言，增加幅度均在5%以内，说明主梁振动对紊流强度的影响相对较小。

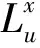
(4) 结构自身振动会造成实测风速功率谱密度函数值略高于实际值的情况，而且这种影响在低频部分更为突出。

必须指出，由于本次试验存在一些不足和可能产生误差之处包括：实验未能够在风洞中进行，以进一步确保来流风场的品质；基底振动仅仅模拟了横风向振动，而实际结构自身的振动包括横风向、顺风向、竖向以及扭转振动等；两风速仪型号不同可能导致的仪器误差等。因此，本文结论有待将来的进一步验证和完善。

[1]Miyata T, Yamada H, Katsuchi H, et al. Full-scale measruments of Akashi-Kaikyo Bridge during typhoon[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90:1517-1527.

[2]Brownjohn J M W, Bocciolone M, Curami A, et al. Humber bridge full-scale measurement campaigns 1990-1991[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1994, 52: 185-218.

[3]Chen Z Q, Wang X Y, Ko J M. Field measurements on wind-rain-induced vibration of bridge cables with and without MR dampers[C]. Proceeding of the 3rd world conference of structural control, Como, Italy, 2002.

[4]Hikami Y, Shiraishi N. Rain-wind induced vibration of cables in cable stayed bridges [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29: 409-418.

[5]李惠, 欧进萍. 斜拉桥结构健康监测系统的设计与实现[J]. 土木工程学报, 2006, 39(4): 39-53.

LI Hui, OU Jin-ping. Design and implementation of health monitoring systems for cable-stayed bridges [J]. China Civil Engineering Journal, 2006, 39(4): 39-53.

[6]Xu Y L, Zhu L D. Buffeting response of long-span cable-supported bridges under skew winds: case study[J]. Journal of Sound and Vibration, 2005(281): 675-687.

[7]王浩, 李爱群, 谢静, 等. 台风作用下超大跨度斜拉桥抖振响应现场实测研究[J]. 土木工程学报, 2010, 43(7): 71-79.

WANG Hao, LI Ai-qun, XIE Jing, et al. Field measurement of the buffeting response of a super-long-span cable-stayed bridge under typhoon [J]. China Civil Engineering Journal, 2010, 43(7):71-79.

[8]Wang Hao, Li Ai-qun, Jiao Chang-ke. Characteristics of strong winds at the Runyang Suspension Bridge based on field tests from 2005 to 2008[J]. Journal of Zhejiang University-Science A, 2010, 11(7): 465-476.

[9]陈政清. 桥梁风工程[M]. 北京:人民交通出版社, 2005.

[10]项海帆. 现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005.

[11]Simiu E, Scanlan R H. Wind effects on structures. 3rd edition, John Wiley & Sons, 1996.

[12]武占科, 赵林, 朱乐东, 等. “罗莎”(0716)台风高空实测脉动风特性分析[J]. 空气动力学学报, 2010, 28(3): 291-296.

WU Zhan-ke, ZHAO Lin, ZHU Le-dong, et al. High-altitude observation about turbulence characteristics for “Krosa” (0716) strong typhoon[J]. Acta Aerodynamica Sinica, 2010, 28(3): 291-296.