锚固条件下矿用锚索中纵向导波传播特性的实验研究

2014-09-07 10:06刘增华何存富

振动与冲击 2014年15期

吴斌，方舟，刘增华，何存富

(北京工业大学机械工程与应用电子技术学院，北京 100124)

矿用锚索加固技术广泛应用于煤矿井下工程，已被证明是一种有效的支护方法。锚索通过钻孔将钢绞线或高强度钢丝绳固定于深部稳定的岩层中，并在被加固表面通过张拉产生预应力，从而达到使被加固体稳定和限制其变形的目的[1]。一旦支护的锚索长度和锚固质量达不到要求，将给煤矿安全生产带来极大的隐患。

矿用锚索一般采用七芯钢绞线。在服役中，为保证矿用锚索与周围岩层紧密接触，两者之间锚固了一层矿用树脂。目前，国外对超声导波检测矿用锚索的研究主要集中于无锚固矿用锚索的传播特性探索[2-3]与预应力大小测量[4-8]，鲜见锚固条件下的矿用锚索的研究。刘增华等[9]采用压电陶瓷片激励和磁致伸缩式传感器接收导波信号的方式研究了0.15 m之内的水泥锚固长度对钢绞线中超声导波的衰减。

本文采用分别作为导波激励源和接收源的两片压电片，针对锚固条件下矿用锚索中纵向超声导波的传播特性进行研究。主要包括1.4m长之内的周围锚固介质对超声导波衰减和波速等影响分析。首先通过简化为细直杆的钢丝中纵向超声导波的频散曲线分析了该模态在无端锚条件下矿用锚索中的传播特性。然后研究了穿透法的方式下L(0,1)模态在水泥锚固条件下矿用锚索中的传播特性。最后对矿用树脂锚固条件下的矿用锚索进行了穿透法的L(0,1)模态的检测实验。

1 矿用锚索中的超声导波纵向模态

在无限均匀各向同性的弹性介质中，只存在2种超声波：纵波和横波[10-11]。超声波在如矿用锚索等有界的介质中传播时，由于受到边界的作用来回反射而形成导波，超声波的相速度因此随频率的变化而变化，这就是超声导波的频散现象[12]。矿用锚索也就是七芯钢绞线。对于七芯钢绞线，无论是外围钢丝还是中心钢丝，均可看做细直杆[13]。超声导波在矿用锚索的传播可以近似简化为在七根细直杆中的传播。

在杆中沿轴向传播的超声波存在纵向模态L(0,m)、扭转模态T(0,m)和弯曲模态F(n,m)等三种不同的模态，其中n和m分别为模态的周向阶次和模数。纵向模态是以只存在径向位移分量和轴向位移分量为特征的超声导波模态，且周向位移分量为0。通过求解波动控制方程可以得到Pochhammer频散方程：

J0(αa)J1(βa)-4k2αβJ1(αa)J0(βa)=0

(1)

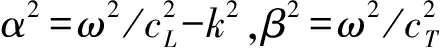
2 实验研究

2.1 水泥锚固条件下矿用锚索的导波检测实验

2.1.1 实验装置

实验装置包括计算机、导波激励接收装置、厚度振动型压电陶瓷片(以下简称压电片)，如图2所示。压电片直径为28 mm，厚9 mm。通过Agilent 4294A精密阻抗分析仪测得该压电片厚度振动方向的谐振频率约为260 kHz。当压电片工作在谐振频率点时，产生的振动能量较大。压电片厚度与谐振频率的关系如式(2)所示[16]

N=f0h

(2)

式中，N为频率常数，在此取2 000 Hz/m。f0为谐振频率，h为压电片的厚度。可以计算得到本实验所用的压电片的谐振频率约为222 kHz。由于频率常数的理论值与实际值并不完全符合，因此理论谐振频率与实际测量值有一些偏差。可见压电片越厚，谐振频率越低。而压电片越厚需要的激励电压越大，因此低谐振频率的压电片对硬件要求较高。而频率越高，导波衰减越大。实验中为了尽量使压电片工作在其谐振频率附近，同时考虑导波激励接收装置的性能，选择了该尺寸的压电片。

通过导波激励接收装置产生10个周期的方波信号来激励压电片，通过耦合剂将两个相同的压电片与矿用锚索的两个端面耦合，采用穿透法检测。其中耦合于两端的两片压电片分别作为导波激励源和接收源。尽管穿透法在工程实际中无法应用，但利用该方法可以在实验室条件下对锚固条件下矿用锚索中超声导波的传播特性进行有效而基础的研究。耦合剂选用蜂蜜，以保证矿用锚索与压电片之间的耦合良好。

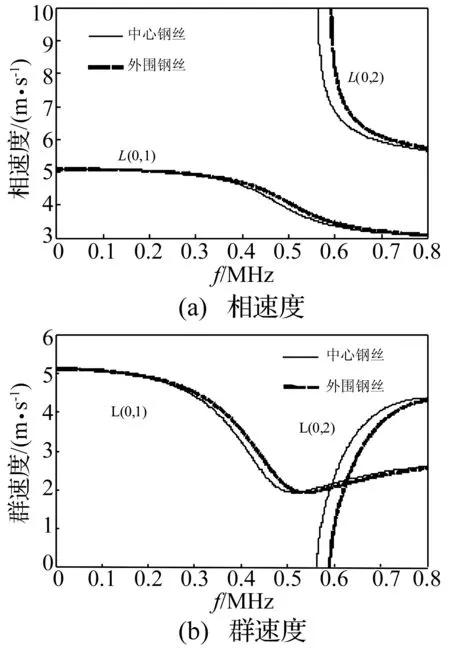
图1 矿用锚索中心与外围钢丝中纵向模态导波频散曲线

2.1.2 实验对象

实验对象为实验室条件下制作的锚固矿用锚索试样，全长6 040 mm。对于岩石中的锚索，在某些条件下，即使采用较大的安全系数，远小于3 m的锚固段长度也已足够[14]。因此本实验研究的最大锚固段长度确定为1 400 mm，如图2所示。由于水泥锚固试样较容易制备，因此实验中首先采用水泥替代矿用树脂对矿用锚索进行锚固，模拟工况锚固条件。由于矿用树脂与水泥的横、纵波波速、密度差别不大[15]，而导波在介质中传播时，主要受这几个参量的影响，因此利用水泥代替矿用树脂是可行的。

矿用锚索试样水泥锚固长度为1 400 mm。然后通过截取水泥层的方法得到不同锚固长度，截取长度间隔为100 mm。实验中采集得到了不同水泥锚固长度下矿用锚索中纵向超声导波的信号。记录的频段为20-500 kHz，频率间隔为5 kHz。

实验分析中，需要确定直达波的最大幅值及导波的群速度。通过LabVIEW编写的专用软件对采集的原始波形先进行小波降噪，再进行希尔伯特包络，得到直达波的最大幅值。其中，利用离散小波变换的方式进行小波降噪，母小波选取的是db14，分解的层数为4，将软阈值作为阈值选取原则，采用多层重构的阈值重构方式。超声导波的群速度由矿用锚索的全长除以直达波波包最大值对应的时间确定。图3为采用穿透法得到的频率280 kHz的L(0,1)模态检测无端锚条件下的矿用锚索的原始波形与信号处理后波形的对比图。图中的直达波包对应的超声导波的群速度为4 355.1 m/s，与图1的中心钢丝、外围钢丝的频散曲线中L(0,1)模态在280 kHz频率点处的群速度较为吻合，因此可以确定实验中激励的是L(0,1)模态。

2.1.3 压电片最佳检测频率的选取

为研究超声导波的幅值与群速度随锚固段长度增加而变化的规律，首先需要确定压电片最适合检测矿用锚索的频率范围。图4为不同端锚锚固长度下L(0,1)模态的幅值图，频段为20-500 kHz。为了方便观察，图中采用了Matlab的高斯插值函数将所有频率的幅值点拟合成一条曲线。拟合时，选择能够反映出数据点变化规律的插值维度。图(a)、(c)利用了6维高斯插值，图(b)、(d)利用了5维高斯插值。幅值越大说明导波能量越大，越适合检测。从图4中可以看出：

(1) 锚固段长度对不同频率的L(0,1)模态衰减程度不同。

从图4(a)中可以看出，在频段20-500 kHz，70 kHz、220 kHz和280 kHz频率点的L(0,1)模态信号存在幅值极大值点，说明比较适合检测无锚固的矿用锚索。但是随着锚固段长度的增加，某些频率的超声导波信号幅值衰减较快。从图4(d)中可以发现频率220 kHz的L(0,1)模态信号的相对幅值较小，因此其在锚固的矿用锚索中衰减较大。同理从图中也可以看出频率280 kHz的L(0,1)模态幅值衰减程度较小。

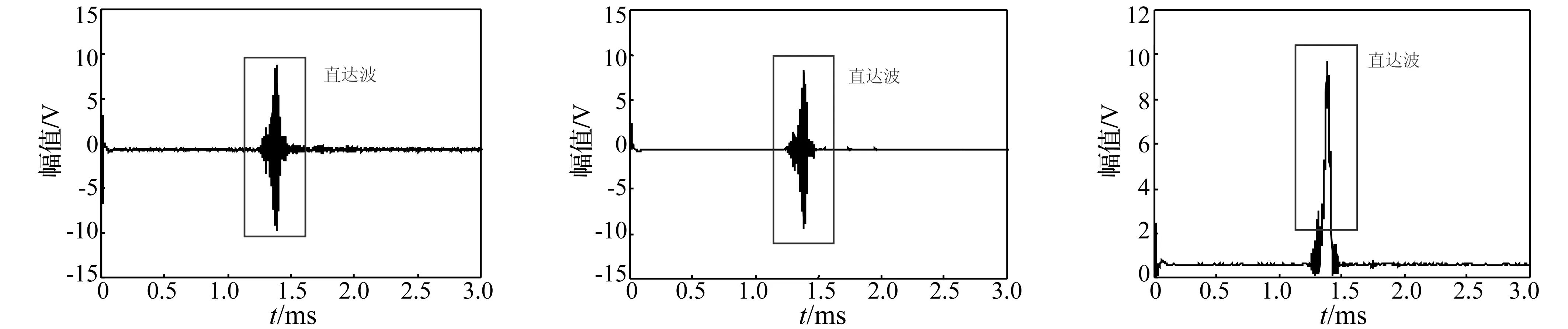
图3 原始波形与信号处理后波形的对比图

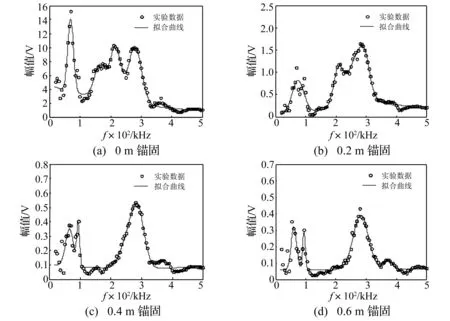
图4 不同水泥锚固长度下在频段20-500 kHz的导波信号幅值

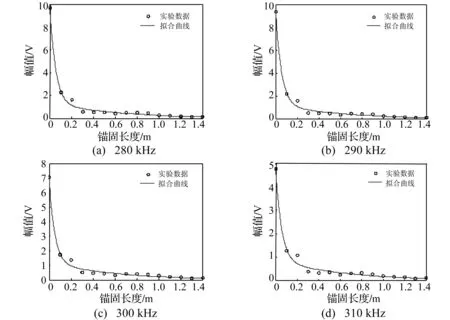
图5 几个频率点下锚固段长度与导波幅值的关系

(2) 实验所使用的压电片在280 kHz频率点处较适合检测锚固条件下的矿用锚索。

如图4(b)、(c)、(d)所示，本实验所使用的压电片在锚固条件下的矿用锚索中，280 kHz的导波信号幅值最大。不仅如此，锚固段长度超过0.6 m之后，其幅值依然是最大的。

由此可见，280 kHz为该压电片对端锚锚固条件下矿用锚索的最佳检测频率。由于锚固长度超过0.6 m之后，其他频率段的直达波已经无法辨识，而低频段的导波信号的分辨率较差，无法得到相对精确的L(0.1)模态导波群速度。因此以下主要研究280 kHz及附近几个频率点的L(0,1)模态在水泥锚固条件下矿用锚索中的传播特性。

2.1.4 矿用锚索水泥锚固段长度对L(0,1)模态的衰减

首先研究不同水泥锚固段长度的矿用锚索对L(0,1)模态信号的衰减。

通过记录不同水泥锚固段长度下，280 kHz、290 kHz、300 kHz、310 kHz频率点直达波的最大幅值，绘制不同锚固长度的矿用锚索与这些频率点的L(0,1)模态信号幅值的关系图，可得到图5。按照2.1.2节中的方法确定直达波的最大幅值。

由图5可知：在所选择的几个检测频率下，矿用锚索水泥锚固段长度小于0.2 m时，L(0,1)模态信号幅值衰减很快，当水泥锚固段长度大于0.2 m之后，信号幅值衰减变缓。其他频率点下的L(0,1)模态幅值衰减也存在这一现象。

2.1.5 矿用锚索水泥锚固长度对L(0,1)模态群速度的影响

本节研究不同水泥锚固段长度的矿用锚索对L(0,1)模态群速度的影响。

通过记录不同水泥锚固段长度矿用锚索中，280 kHz、290 kHz、300 kHz、310 kHz频率点的L(0,1)模态群速度，图6绘制矿用锚索的水泥锚固段长度与这些频率点L(0,1)模态导波群速度的关系曲线。从图中可以看出，对于所选择几个频率点的L(0,1)模态，矿用锚索水泥锚固长度小于0.4 m时，群速度随水泥锚固长度的增长近似线性地下降。水泥锚固长度每增长0.1 m，群速度就下降44 m/s。而水泥锚固长度大于0.4 m之后波速变化较小，趋于震荡。

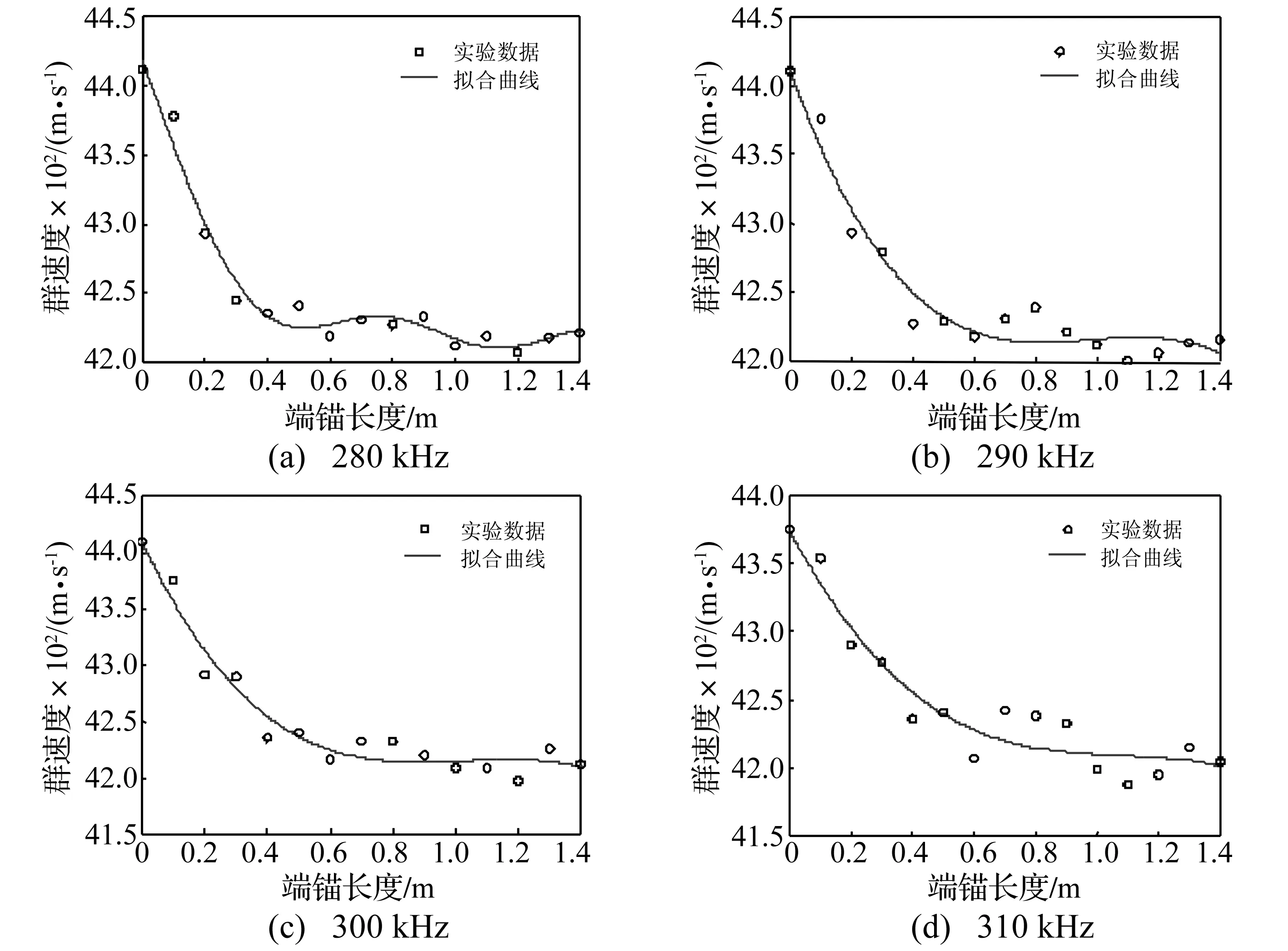
图6 几个频率点下水泥锚固段长度与L(0,1)群速度的关系

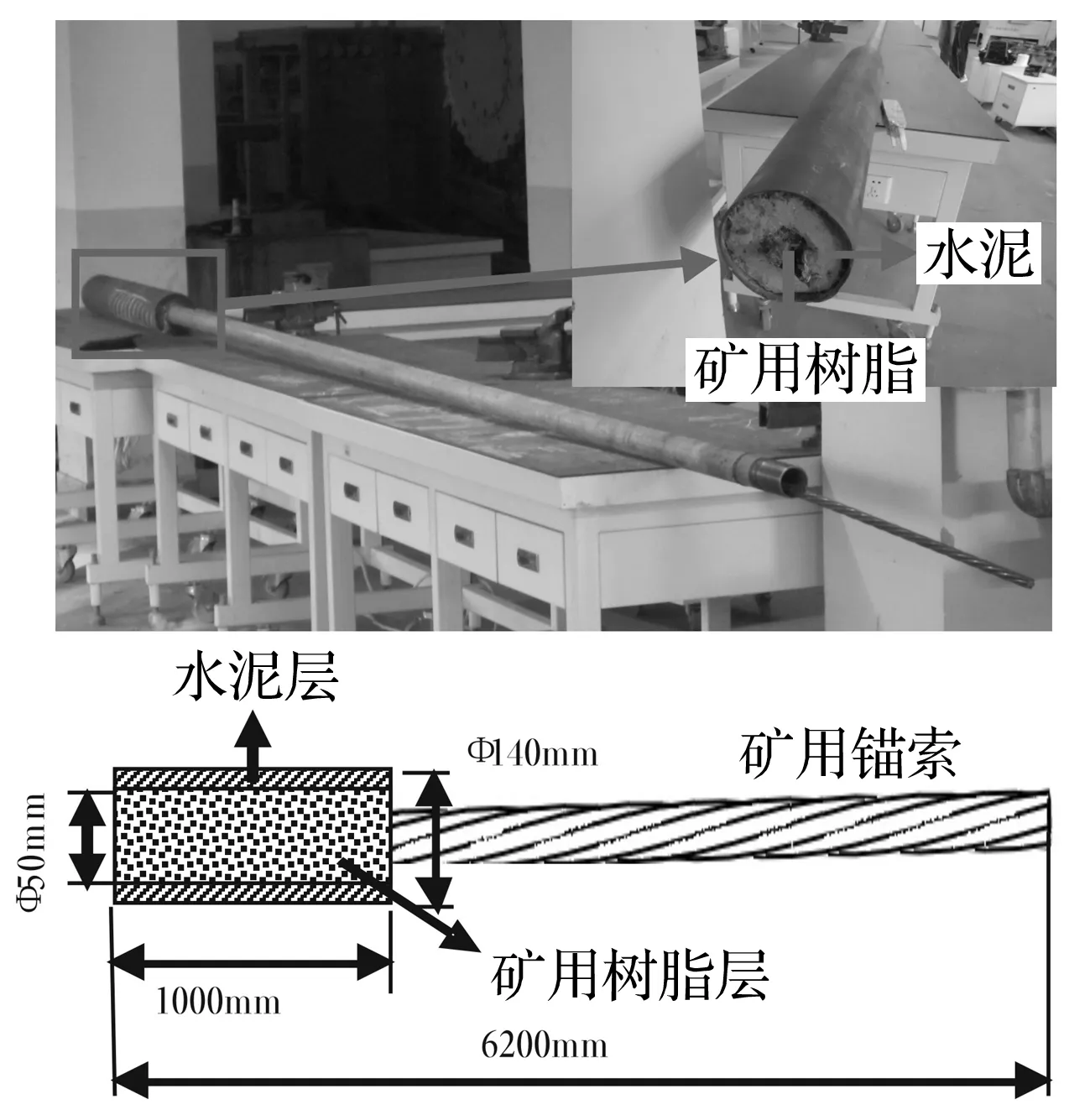
图7 矿用树脂锚固条件下的矿用锚索及其示意图

2.2 矿用树脂锚固条件下矿用锚索的导波检测实验

在水泥锚固条件下矿用锚索导波检测研究的基础上，为更接近实际工况，实验制备了矿用树脂锚固的矿用锚索试样，研究在该试样中超声导波的传播特性。矿用树脂锚固条件下的矿用锚索试样如图7所示。该矿用锚索试样长6 200 mm，锚固段长度1 000 mm。其中，矿用树脂层外直径为50 mm，握裹锚索厚约15 mm，矿用树脂层外握裹着厚45 mm的水泥层，水泥外层直径140 mm，水泥外壁为一圆管。

在该实验中采用穿透法检测，激励频率设置为300 kHz，周期数为4，实验装置与2.1.1节中相同。利用2.1.2节中确定直达波最大幅值的方法，得出直达波最大幅值为0.269 V。图5(c)的曲线图可以看出该信号幅值对应1 m左右的水泥锚固段长度，与该矿用锚索锚固段长度接近。利用2.1.2节中确定导波群速度的方法，计算得到直达波的传播速度为4 233.6 m/s，与图6(c)中1 m水泥锚固长度的群速度相近。这进一步说明纵向模态L(0,1)在水泥锚固条件下与矿用树脂锚固条件下的矿用锚索中传播特性较为相似，并且利用水泥替代矿用树脂制备工程锚固条件下矿用锚索是合理的。

3 结论

(1) 利用厚度振动型压电陶瓷片在穿透法的检测方式下，得到频段20-500 kHz内L(0,1)模态的幅值曲线随矿用锚索的水泥锚固段长度增长而变化的现象，表明水泥锚固段长度对不同频率的L(0,1)模态衰减程度不同，且优化选取频率280 kHz为压电片的最佳检测频率。

(2) 通过穿透法的检测方式，实验研究了水泥锚固条件下的矿用锚索锚固段长度对280 kHz附近几个频率点下L(0,1)模态的衰减与群速度的影响。首先，0.2 m之前，矿用锚索水泥锚固段长度增长对L(0,1)模态的信号幅值衰减较大，0.2 m之后，衰减变缓；其次，0.4 m之前，随着水泥锚固段长度的增加，该模态的群速度近似线性地下降，水泥锚固段长度每增长0.1 m，L(0,1)模态的群速度就下降44 m/s。超过0.4 m之后，群速度变化不明显。

(3) 矿用树脂锚固条件下的矿用锚索穿透法的实验结果符合水泥锚固条件下的矿用锚索锚固段长度与导波信号幅值、群速度的关系曲线。但是由于锚固段长度大于一定值后，群速度与信号幅值的变化都不明显，因此若要通过超声导波检测结果准确判断矿用锚索锚固段的长度，还需进一步的研究。

[1]韩洪亮,郭建明,黄爱悦,等. 矿用锚索检测方法的研究[J]. 煤炭科学技术,2004,32(9):58-60.

HAN Hong-liang, GUO Jian-ming, HUANG Ai-yue, et al. Research on mine anchor inspection method[J]. Coal Science and Technology, 2004,32 (9):58-60.

[2]Treyssede F. Numerical investigation of elastic modes of propagation in helical waveguides[J]. Journal of the Acoustical Society of America,2007,121(6):3398-3408.

[3]Treyssede F, Laguerre L. Investigation of elastic modes propagating in multi-wire helical waveguides[J]. Journal of Sound and Vibration, 2010,329(10):1702-1716.

[4]Chen H L, Wissawapaisal K. Measurement of tensile forces in a seven-wire prestressing strand using stress waves[J]. Journal of Engineering Mechanics,2001, 127 (6):599-606.

[5]Di Scalea F L, Rizzo P. Stress measurement and defect detection in steel strands by guided stress waves[J]. Journal of Materials in Civil Engineering, 2003,15(3): 219-227.

[6]Rizzo P. Ultrasonic wave propagation in progressively loaded multi-wire strands[J]. Experimental Mechanics, 2006,46(3):297-306.

[7]Chaki S, Bourse G. Guided ultrasonic waves for non-destructive monitoring of the stress levels in prestressed steel strands[J]. Ultrasonics,2009,49(2):162-171.

[8]刘溯,刘增华,何存富,等. 钢绞线中纵向模态衰减特性的试验研究[J]. 建筑结构学报,2007,S1:179-183.

LIU Su,LIU Zeng-hua,HE Cun-fu,et al. Experimental research on attenuation characteristics of longitudinal modes guided wave in steel strands[J]. Journal of Building Structures,2007,S1:179-183.

[9]刘增华,刘溯,吴斌,等. 预应力钢绞线中超声导波声弹性效应的试验研究[J]. 机械工程学报,2010,46(2):22- 27.

LIU Zeng-hua, LIU Su, WU Bin, et al. Experimental research on acoustoelastic effect of ultrasonic guided waves in prestressing steel strand[J]. Journal of Mechanical Engineering,2010,46(2):22-27.

[10]刘增华,张易农,张慧昕,等. 基于磁致伸缩效应在钢绞线中激励接收纵向导波模态的试验研究[J]. 机械工程学报,2010,46(6):71-76.

LIU Zeng-hua, ZHANG Yi-nong, ZHANG Hui-xin, et al. Experimental research on excitation and reception of longitudinal guided wave modes in steel strands based on magnetostrictive effect[J]. Journal of Mechanical Engineering, 2010,46(6):71-76.

[11]刘增华,何存富,王秀彦,等. 钢绞线中纵向模态传播特性的实验研究[J]. 北京工业大学学报,2008,34(9): 897-901.

LIU Zeng-hua, HE Cun-fu, WANG Xiu-yan, et al. Experimental research on propagation characteristics of longitudinal modes in steel strands[J]. Journal of Beijing University of Technology,2008,34(9):897-901.

[12]刘增华,张易农,何存富,等. 钢绞线中激励纵向模态的磁致伸缩型激励及接收器的选型[J]. 应用力学学报, 2009,26(3):507-512.

LIU Zeng-hua, ZHANG Yi-nong, HE Cun-fu, et al. Development of magnetostrictive transmitter and receiver for exciting ultrasonic longitudinal guided waves in steel strands[J]. Chinese Journal of Applied Mechanics, 2009,26(3):507-512.

[13]刘增华,赵继辰,吴斌,等. 高阶纵向超声导波在钢绞线缺陷检测中的应用研究[J]. 工程力学,2011,28(8): 214-220.

LIU Zeng-hua, ZHAO Ji-chen, WU Bin, et al. Application study on defect detection in steel strands by using high-order ultrasonic longitudinal guided waves[J]. Engineering Mechanics, 2011,28(8):214- 220.

[14]杨晓东. 锚固与注浆技术手册[M]. 北京：中国电力出版社,2009.

[15]崔江余,孙雅欣,何存富. 全长粘结型树脂锚杆低频超声导波检测应用研究[J]. 工程力学,2010,27(3):240-245.

CUI Jiang-yu, SUN Ya-xin, HE Cun-fu. Application of low frequency ultrasonic guided waves on inspection of full-length-bonding resin bolt[J]. Engineering Mechanics, 2010,27(3):240-245.