考虑时间谐波电流的永磁同步电机电磁噪声阶次特征分析
马琮淦,左曙光,孙 庆,孟 姝
(同济大学 新能源汽车工程中心,上海 201804)
分布式驱动电动汽车具有多工况、变负载、宽调速等特点,主要采用变频调速永磁同步电机直接驱动,其噪声问题呈现新的特点[1]:变频器供电产生大量的时间谐波电流,使气隙磁场也产生大量的谐波磁场,显著影响径向力波的幅值和阶次,并且可能导致径向力波频率与永磁同步电机或电动汽车车身的某些模态频率接近而发生共振,进而引起永磁同步电机甚至整车的振动和噪声的显著增大。因此,通过实验和理论分析的手段,对考虑时间谐波电流的永磁同步电机电磁噪声进行研究具有重要意义。
Wallace等[2]通过研究感应电动机、永磁直流无刷电动机、开关磁阻电动机,发现了变频器供电已成为电机振动和噪声的主要来源之一,指出应充分考虑控制系统对电磁噪声的影响。Ronnie等[3]提出了变频器对感应电动机电磁噪声的四步研究法:首先分析变频器的频谱,其次根据电动机的数据对电磁力进行谱分析,然后计算定子结构的模态,最后将电磁力频谱和定子模态进行对照。Garcia-Otero等[4]应用改进的脉宽调制控制方法,消除了逆变器中对电动机共振频率敏感的电流谐波。Bi等[5]分析了噪声频率、谐波电流和谐波磁场的关系。唐任远等[6]通过有限元法计算变频器供电时永磁同步电机的三维声场,预估并实验验证了开关频率处的噪声峰值频率。使用环境的不确定性和工况的多样性使分布式驱动电动汽车用永磁同步电机的时间谐波电流相对于普通工业驱动用永磁同步电机更加丰富,噪声问题也更加突出、复杂。虽然文献[7]考虑了时间谐波电流,系统地研究了电动车用永磁同步电机转矩波动阶次特征,但转矩波动是车身阶次振动和车内噪声的主要源头,而非永磁同步电机电磁噪声的主要源头[8],其阶次特征也与电磁噪声的阶次特征差异较大。永磁同步电机电磁噪声的主要源头是径向力波[8-9],径向力波的阶次特征可表征永磁同步电机电磁噪声的阶次特征。然而,鲜有文献考虑时间谐波电流,研究电动车用永磁同步电机电磁噪声的阶次特征。
本文首先通过噪声测试实验总结了变频器供电下分布式驱动电动车用永磁同步电机电磁噪声的阶次特性,然后建立了考虑时间谐波电流的永磁同步电机电磁噪声的数学模型,通过该模型对电磁噪声阶次进行了预测。
1 分布式驱动电动车用永磁同步电机噪声实验与分析
1.1 实验方案与实施
实验目的是通过测量多工况下分布式驱动电动车用永磁同步电机噪声信号,总结噪声特性,为发生机理的分析奠定基础。实验对象为某国产电动车用永磁同步电机,该电机为星形连接,其参数如表1所示。

表1 永磁同步电机的参数

图1 噪声测量实验设备
实验采用台架实验的方法。实验工况为:① 保持负载转矩20 N·m恒定,控制电机以300 r/min、400 r/min、500 r/min的转速匀速运行,测量噪声信号;② 保持转速500 r/min恒定,控制电机以10 N·m、20 N·m、30 N·m、40 N·m的负载转矩运行,测量噪声信号。噪声测量实验设备如图1所示。
1.2 实验数据的处理与分析
在电动车用永磁同步电机匀速运行过程中,噪声信号表现为平稳信号,可通过快速傅里叶变换得到噪声声压级的频谱图。图2为相同负载转矩20 N·m、不同转速下永磁同步电机噪声频谱图,图3为相同转速500 r/min、不同负载转矩下永磁同步电机噪声频谱图。

图2 不同转速、相同负载转矩的永磁同步电机噪声频谱
实验中,电源频率为f0=pn/60,其中p为极对数12,n为电机转速。故,转速300 r/min、400 r/min、500 r/min对应的电源频率分别为60 Hz、80 Hz、100 Hz。背景噪声总声压级为51.35 dB(A),试验中可忽略背景噪声的影响,不需要对噪声测试结果进行修正。图2、图3中,定义“阶次”为噪声峰值频率与电源频率的比值。
因此,由图2和图3可得以下结论与分析:
(1) 永磁同步电机噪声表现出明显的阶次特性,主要含有偶数阶谐波噪声,对应噪声峰值频率为电源频率的偶数倍频。这与文献[8]的结论基本一致,主要由基波电流产生的谐波磁势和永磁体谐波磁势相互作用产生的。
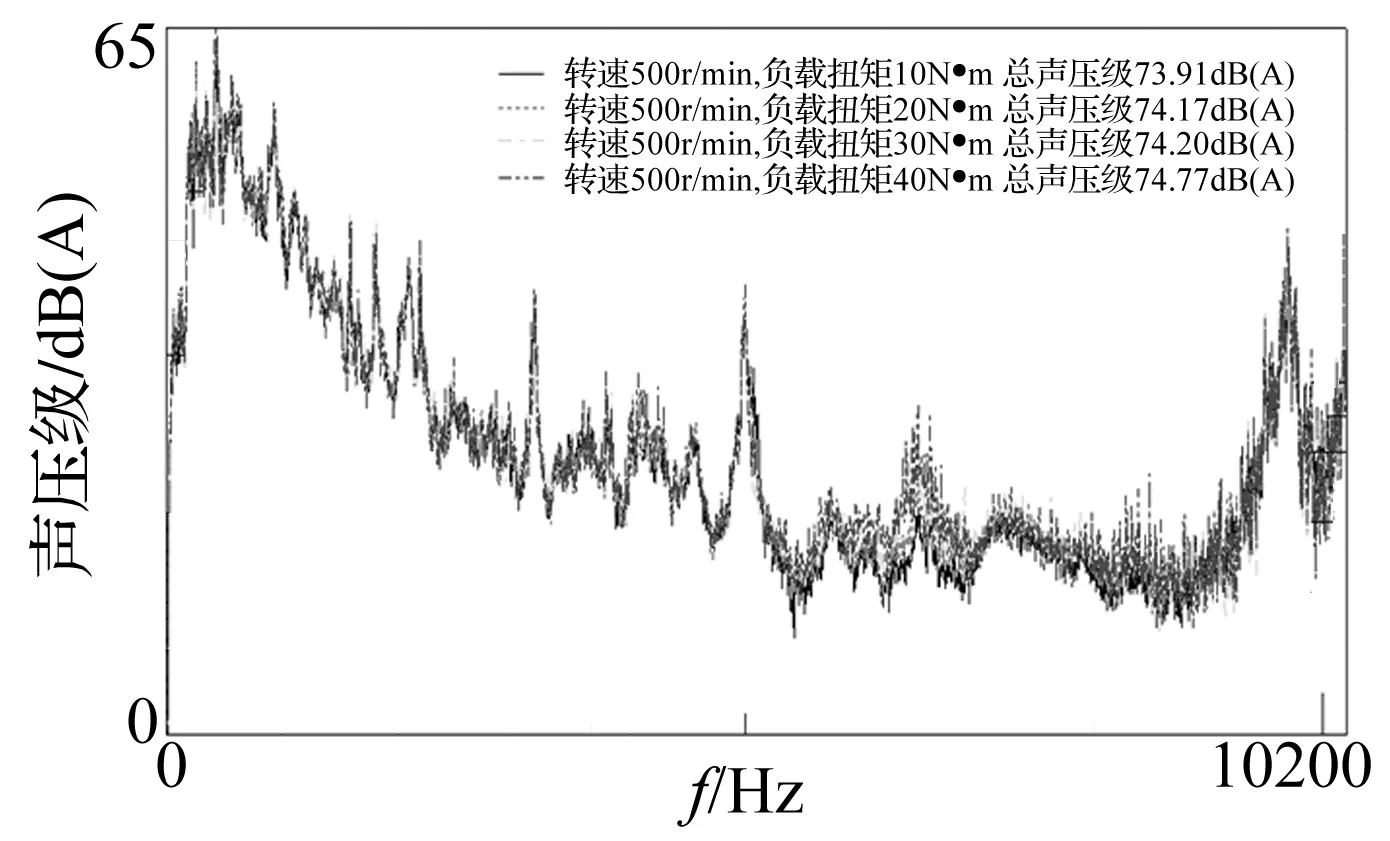
图3 相同转速、不同负载转矩的永磁同步电机噪声频谱
(2) 变频器开关频率(本实验是10 000 Hz)附近存在显著的噪声峰值。这与文献[6]的结论基本一致,主要由开关频率相关的空间气隙磁场谐波作用产生。
(3) 除此之外,还存在大量的奇数阶和分数阶谐波噪声。
结论(3)鲜有文献提及与分析。因此,本文旨在建立统一的解析模型,揭示偶数阶次、开关频率附近阶次、奇数阶次、分数阶次电磁噪声的产生机理。
2 噪声阶次特性产生机理的理论分析
为了解释实验中永磁同步电机噪声阶次特性的实验现象,本文建立了考虑时间谐波电流的永磁同步电机噪声计算的解析模型。
2.1 气隙磁势
为便于分析,作如下假设:① 磁路不饱和;② 忽略铁心磁路磁阻的影响;③ 线性的磁性条件;④ 定子槽是矩形或梯形槽。⑤ 定子绕组中含有大量的h次时间谐波电流(h的取值,可由相电流的频谱分析确定)。
从电机学理论可知:正弦波供电时,永磁电机中的气隙磁势可以分为定子电流谐波磁势和转子永磁体等效磁势。
采用变频器供电的永磁电机与采用正弦波供电时相比,定子磁势将分为基波电流产生的定子磁势和所有的h次时间谐波电流产生的定子谐波磁势。其中所有的h次时间谐波电流产生的定子谐波磁势是变频器供电条件下所特有的也是引起永磁电机振动和噪声过大的主要原因。气隙磁势可表示为:
(1)
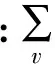
定子基波电流产生的磁势是因为定子绕组的非正弦分布而由定子基波电流产生的,可表示为:
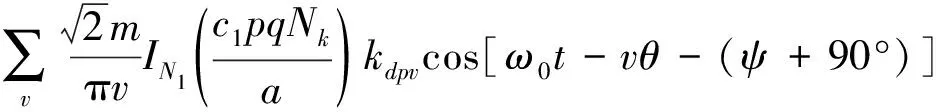
式中,IN1为基波电流有效值,v为谐波次数,m为永磁同步电机的相数,c1为绕组层数,p为极对数,q为每极每相槽数,Nk为线圈匝数,a为并联支路数,kdpv为绕组因数,ω0为基波电角速度,ψ为基波电流的功角。
当定子绕组非正弦分布时,所有的h次时间谐波电流也会产生定子谐波磁势,可表示为:
vθ-(ψh+90°)]=
vθ-(ψh+90°)]
(3)
式中,Ih为h次时间谐波电流的幅值,ψh为h次时间谐波电流的功角。
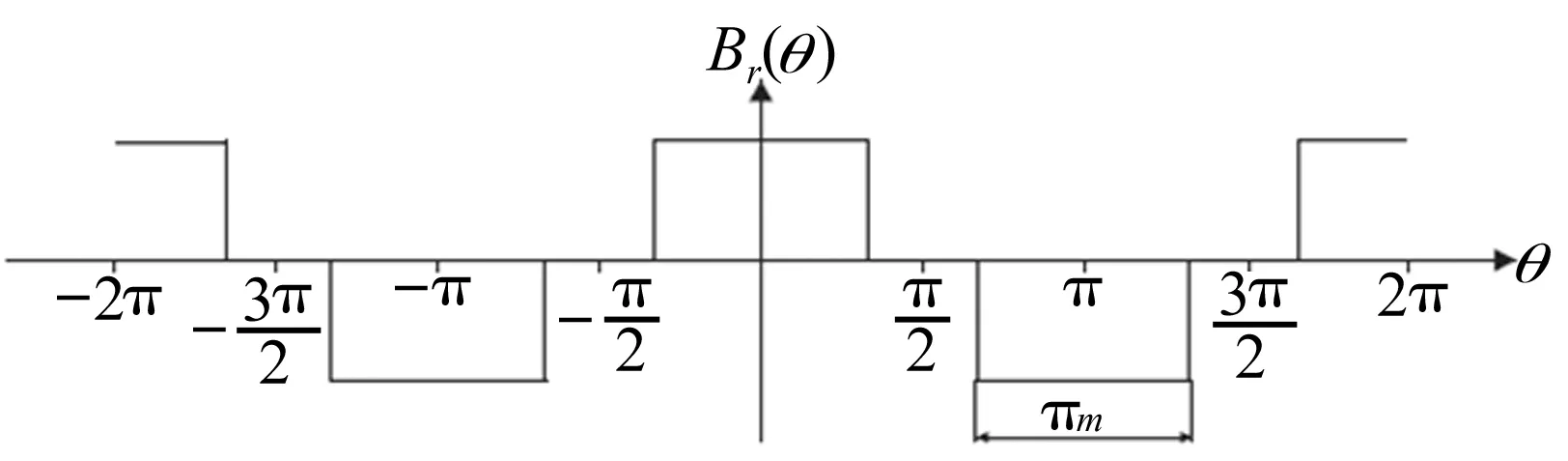
图4 永磁体磁场分布
假定永磁体磁场沿转子有效极弧为矩形分布,如图4,通过傅里叶级数分解,可得永磁体磁势可表示为:
(4)
式中,δ为气隙长度,μ0为真空磁导率,Br为永磁体剩磁,τm为极弧角。
综上所述,将式(2)~式(4)代入到式(1),可得气隙磁势:
vθ-(ψ+90°)]+
vθ-(ψh+90°)]+
(5)
2.2 气隙磁导
开槽以两种方式影响磁场。首先,减少了每极磁通,通常通过引入卡特系数Kc计算此效应;其次,影响永磁体和气隙内的磁场分布。本文采用文献[10]中开槽气隙区域的2维开槽模型相对磁导函数λ(θ)来计算,可推得:
(6)
式中:y1是绕组节距,Qs是槽数,Λk的表达式如下:
(7)
Λk=
(8)
式中,b0是槽宽度,Kc卡特系数,β(r)为保角变换系数,Rs为定子半径。
2.3 气隙磁通密度
考虑所有的h次时间谐波电流的永磁同步电机气隙磁通密度可由气隙磁势与气隙磁导的乘积求得:
b(θ,t)=f(θ,t)λ(θ)=
ω0t-(ψ+90°)]+
cos[(kQs+v)θ+ω0t-(ψ+90°)]}+
v)θ+hω0t-(ψh+90°)]+
cos[(kQs+v)θ-hω0t+(ψh+90°)]}+
(2μ-1)p)θ+(2μ-1)ω0t]+
cos[(kQs+(2μ-1)p)θ+(2μ-1)ω0t]
(9)
为不失一般性,将基波电流也考虑为h=1的时间谐波电流,并在所有h次时间谐波电流中任取hi次和hj次时间谐波电流,故由式(9)可得永磁同步电机气隙磁通密度的频率为:hif0、hjf0、(2μ-1)f0。
2.4 径向力波和径向集中电磁力
利用麦克斯韦定律求出转子内表面单位面积上的径向力波pn(θ,t)为[8-9]:
(10)
将式(9)代入式(10),可得径向力波的频率为:2hif0、2hjf0、2(2μ-1)f0、(hi±hj)f0、(2μ-1±hi)f0、(2μ-1±hj)f0。
将单位面积上的径向力波转化为集中力,可通过沿转子内表面对径向力波积分实现:
(11)
式中:lr为转子轴向长度,rr为转子内半径。
径向集中电磁力的频率与径向力波的频率相同。由于pn(θ,t)的复杂性,求pn(θ,t)的原函数Pn(θ,t)非常困难,以致计算式(11)非常困难。本文采用复合柯特斯公式求解此定积分,具体做法是:将积分区间[0,2π]分成4等分,步长为y=(2π-0)/4=π/2,节点为θi=iy,(i=0,1,2,3,4),在每一个小区间[θi,θi+1]上应用柯特斯公式,即得到复合柯特斯公式的定积分近似解。该解具有6阶代数精度:
(12)
式中:
2.5 永磁同步电机外转子系统振动分析
分布式驱动用永磁同步电机一般采用圆柱形的表贴式外转子型式,与普通工业驱动用外定子永磁同步电机的不同之处是:外转子为声辐射体。由于外转子采用规则的圆柱形,因此,可借鉴以前分析圆柱形外定子系统振动分析,将外转子简化为两端轴承简支的圆柱壳。应用Donnell-Mushtari的壳理论[11]描述壳体的振动,圆柱壳表面振动方程为:
(13)

对式(13)求特征根,得两端简支外转子系统的固有频率:
(14)
式中,Ωmn对应于每阶模态(m,n)的固有频率fmn,ωmn为外转子固有圆频率。
外转子系统的振动响应都是全部模态的叠加。当电磁径向集中力的激励频率接近或等于外转子系统的固有频率时,外转子系统将发生共振,振动响应将以该阶振动模态进行振动,而其他阶振动模态分量振幅非常小,此时,径向位移为:
(15)
式中,Frmn为(m,n)阶模态频率对应的电磁径向集中力(可通过式(12)傅里叶级数分解求得),M为外转子系统的质量,ωr为电磁径向集中力的频率,ζmn为模态阻尼比。
2.6 永磁同步电机声辐射的计算与阶次频率分析
永磁同步电机外转子在径向力波的作用下振动,从而引起电磁噪声。本文采用有限长圆柱形声辐射模型[12]计算声功率:
(16)
式中:ρ0为介质密度(对于空气ρ0=1.186 kg/m3),C为介质中声波传播的速度(对于空气C=344 m/s),IcL(ωr)为相对声强系数。
由于永磁同步电机外转子系统振动属于径向力波激励下的强迫振动,因此,外转子振动频率与径向力波的频率相同。又由式(16)可得,电磁噪声的特征频率应与外转子振动频率相同,亦即电磁噪声的特征频率为2hif0、2hjf0、2(2μ-1)f0、(hi±hj)f0、(2μ-1±hi)f0、(2μ-1±hj)f0,故电磁噪声的特征阶次为2hi、2hj、2(2μ-1)、(hi±hj)、(2μ-1±hi)、(2μ-1±hj)。当时间谐波电流的阶次hi或hj是分数时,电磁噪声将出现分数阶特征频率。由式(9)、(10)、(15)、(16)可得:永磁同步电机电磁振动和电磁噪声特征频率处的幅值由激励源和定转子结构固有特性共同决定,当激励源频率与固有频率相同或相近时,将引发共振并产生较大噪声。
3 数值模拟与实验现象的验证
为了依据本文理论分析解释实验中出现的谐波阶次与频率,实验中采集了相同负载转矩20 N·m、不同转速下永磁同步电机B相电流信号频谱图,如图5;其频谱特性,如图6。
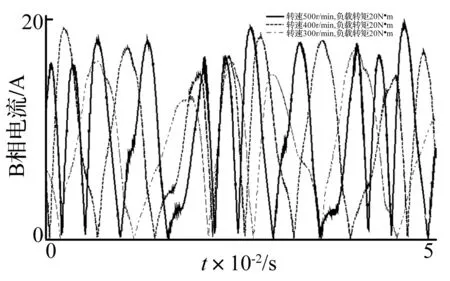
图5 B相电流的时间历程
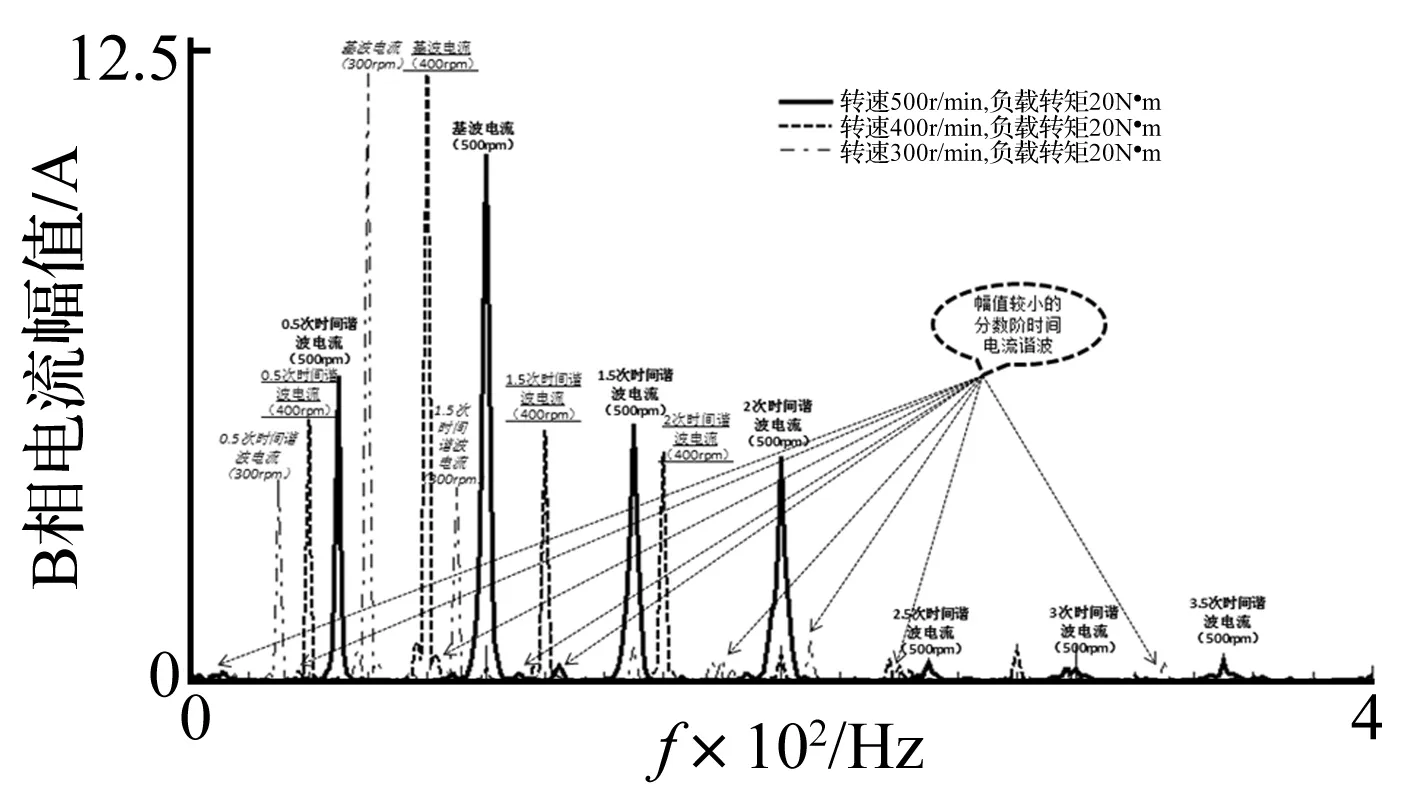
图6 B相电流的频谱图
永磁同步电机的基波电流频率为f=pn/60,式中p为极对数,n为电机转速;时间谐波电流阶次h=fh/f,式中fh为h次时间谐波电流频率,可由相电流频谱分析得到。由图6可知:式(3)中,转速500 r/min、负载转矩20 N·m时,基波电流频率为100 Hz,h的取值集合为h500∈{0.1,0.5,1,1.1,1.3,1.5,1.9,2,2.5,2.9,3,3.5,95,96,97,98,100.8,102},其中幅值较大的时间谐波电流阶次用加粗的斜体数字和灰色底纹标记;转速400 r/min、负载力矩20 N·m时,h的取值集合为h400∈{0.09,0.5,1,1.25,1.5,2,2.5,2.96,3,3.5,4,4.5,5,5.5,6,7,8,9,9.5,120,121,122,123,127};转速300 r/min、负载力矩20 N·m时,h的取值集合为h300∈{0.25,0.45,0.5,0.95,1,1.05,1.25,1.5,2,2.5,2.95,3,3.1,3.5,4.5,5,5.5,6,161.7,162.2,162.7,163.6,164.6}。μ的取值集合为μ∈N*。故,将转速500 rpm、负载转矩20N·m时永磁同步电机电磁噪声阶次预测值列入表2;将实验结果图2中也出现的阶次值用斜体数字和灰色底纹标记,如表2所示,限于篇幅,μ仅取1、2、3,对0-1 000 Hz和开关频率附近的电磁噪声阶次进行验证,其余频段内验证方法相同。
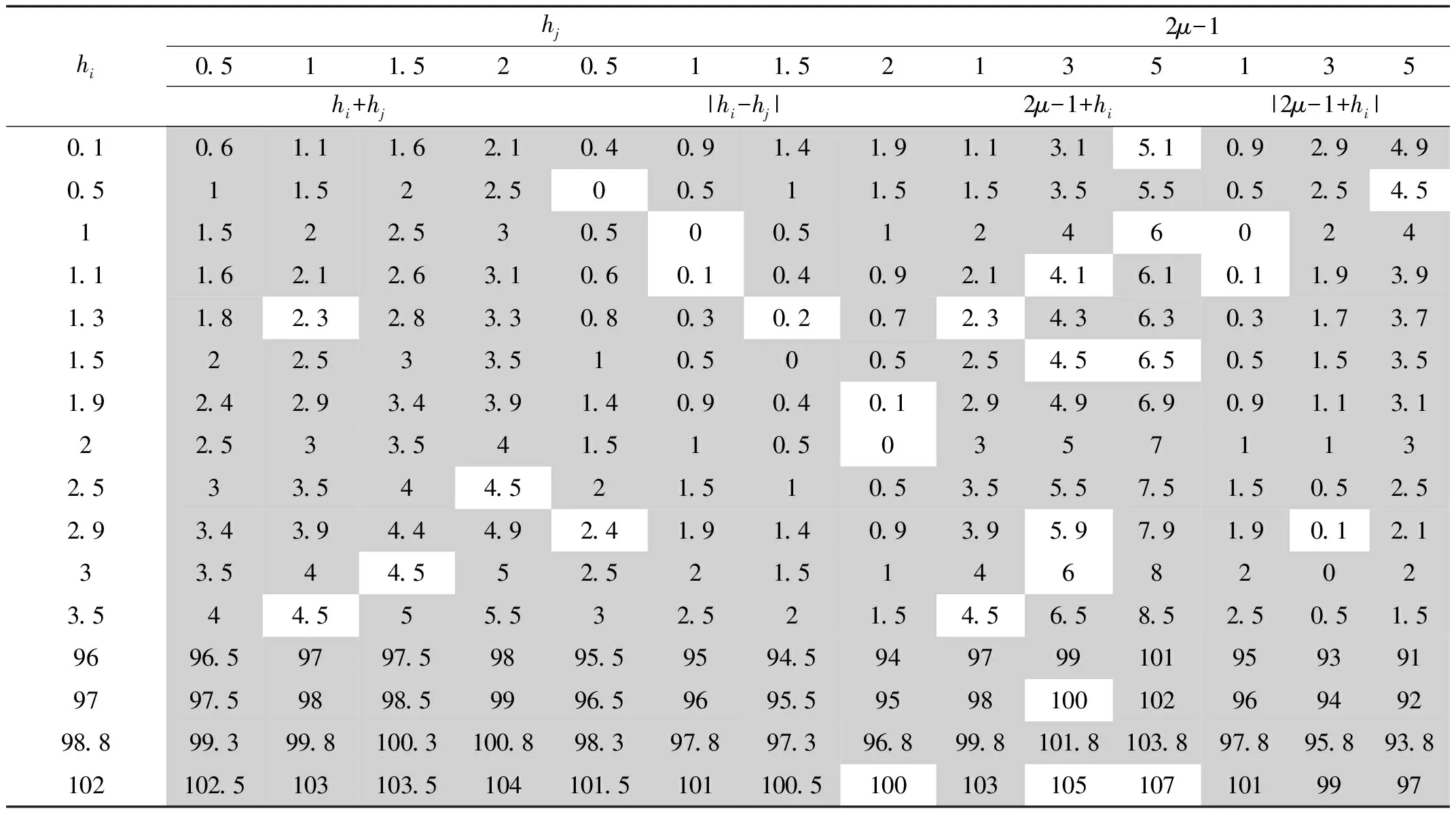
表2 理论分析阶次预测值(500 r/min,20 N·m)
由表2可知:转速500 r/min负载力矩20 N·m时,实验中出现的电磁噪声阶次和频率均能通过本文的理论分析预测到,进而能找到产生该阶次转矩波动的机理,例如102阶电磁噪声由96次时间谐波电流和3阶永磁体磁势产生,而1.1阶电磁噪声由0.1次时间谐波电流和基波电流作用产生,0.1次时间谐波电流和1阶永磁体磁势作用产生,1.9次时间谐波电流和3阶永磁体磁势作用产生。同理易得另外两种工况(400 r/min/20 N·m和300 r/min/20 N·m)电磁噪声阶次和频率的理论预测与实验对比,限于篇幅,本文不再列出。可见,本文的数学模型能合理的解释永磁同步电机电磁噪声的阶次特征现象。
4 结 论
(1) 对分布式驱动电动车用永磁同步电机进行了噪声测试实验与阶次分析,实验结果表明电磁噪声具有明显的阶次特征,主要阶次不仅包含偶数阶、开关频率附近阶次,还包含了大量奇数阶、甚至以往研究中被当做信号毛刺而忽略的分数阶。
(2) 建立了考虑时间谐波电流的永磁同步电机电磁噪声计算解析模型,理论分析发现:电磁噪声的特征
阶次为2hi、2hj、2(2μ-1)、(hi±hj)、(2μ-1±hi)、(2μ-1±hj)。当时间谐波电流的阶次hi或hj是分数时,电磁噪声将出现分数阶特征频率。经过与实验结果对比,本模型能精确预测和解释永磁同步电机电磁噪声的阶次与频率。
[1]王建, 张立军, 余卓平, 等. 燃料电池轿车电机总成的振动阶次特征分析[J]. 汽车工程, 2009, 31(3): 219-223.
WANG Jian, ZHANG Li-jun, YU Zhuo-ping, et al. An analysis on the vibration order feature of the electric motor assembly in a fuel cell car[J]. Automotive Engineering, 2009, 31(3): 219-223.
[2]Wallace A K, Spee R, Martin L G. Current harmonics and acoustic noise in AC adjustable-speed drives[J]. IEEE Transactions On Industry Applications,1990, 26(2): 267-273.
[3]Belmans R J M, Verdyck D, Geysen W. Electro-mechanical analysis of the audible noise of an inverter-fed squirrel-cage induction motor[J]. IEEE Transactions On Industry Applications,1991, 27(3): 539-544.
[4]Garcia-Otero S, Devaney M. Minimization of acoustic noise in variable speed induction motors using a modified PWM drive [J]. IEEE Transactions On Industry Applications, 1994, 30(1): 111-115.
[5]Bi C, Jiang Q, Lin S, et al. Reduction of acoustic noise in FDB spindle motors by using drive technology[J]. IEEE Transactions On Magnetics, 2003, 39(2): 800-805.
[6]唐任远, 宋志环, 于慎波, 等. 变频器供电对永磁电机振动噪声源的影响研究[J]. 电机与控制学报, 2010, 14(3): 12-17.
TANG Ren-yuan, SONG Zhi-huan, YU Shen-bo, et al. Study on source of vibration and acoustic noise of permanent magnet machines by inverter[J]. Electric Machines and Control, 2010, 14(3): 12-17.
[7]马琮淦, 左曙光, 杨德良, 等. 电动车用永磁同步电机转矩波动的阶次特征分析[J]. 振动与冲击, 2013, 32(13): 81-87.
MA Cong-gan, ZUO Shu-guang, YANG De-liang, et al. Order feature analysis of torque ripple in permanent magnet synchronous motor for electric vehicle[J]. Journal of Vibration and Shock, 2013, 32(13): 81-87.
[8]陈永校, 诸自强, 应善成. 电机噪声的分析和控制[M]. 杭州: 浙江大学出版社, 1987, 43-45.
[9]YU Shen-bo, TANG Ren-yuan. 9.Electromagnetic and mechanical characterizations of noise and vibration in permanent magnet synchronous machines[J]. IEEE Transactions on Magnetics, 2006, 42(4):1335-1339.
[10]Zhu Z Q, Howe David. Instantaneous magnet field distribution in brushless permanent magnet dc motors,Part 3:effect of stator slotting[J]. IEEE Transactions on Magnetics, 1993, 29(1):143-150.
[11]Soedel W. Vibrations of shells and plates[M]. New York: Marcel Dekker, 2004, 207-255.
[12]Gieras J F, Wang C, Lai J C. Noise of polyphase electric motors[M]. Boca Raton: CRC, 2006, 127-171.

