基于时程分析的滑塌式危岩清除爆破动力稳定性计算方法

陈洪凯，周云涛，唐红梅

(重庆交通大学 岩土工程研究所，重庆 400074)

危岩(unstable rock)是指由多组岩体结构面切割并位于陡崖或陡坡上稳定性较差的岩石块体及其组合[1]。危岩崩塌是山区主要地质灾害类型及灾害地貌过程，仅在长江三峡库区重庆境内便有5万多个危岩体，单个体积达8 000 m3，威胁着80多万人生命和数百亿财产安全[2]。危岩崩塌具有范围广、规模大、灾情严重等特点，灾害一旦发生，将造成严重的后果。因此，进行危岩稳定性系统评价及机制分析，对于危岩防灾减灾具有积极意义。

重庆市地方标准《地质灾害防治工程勘察规范》DB50/143-2003[3]将危岩体分为滑塌式、坠落式和倾倒式三种，基于刚体极限平衡给出了三种危岩体的稳定性计算方法，陈洪凯等[4-6]对此三种方法作了详细分析和介绍，并将断裂力学应用于危岩体稳定性计算，推导出滑塌式、坠落式和倾倒式危岩的第一类断裂强度因子和第二类断裂强度因子计算公式，建立了一种新的危岩体稳定性计算方法。在危岩体治理方面，对于危岩体下方坡度比较平缓、具有0.5-1.0倍陡崖高度的地形平台且平台上无重要建构筑物及居民居住或崖下方具有有效防御措施时，可采用清除处理，常用的危岩体清除方法有风枪凿岩、人工凿石、静态爆破剂等，对于大型危岩体，常采用浅孔松动爆破[7]。爆破清除危岩体过程中，炸药爆炸产生的爆破动力对危岩体进行作用，致使危岩体稳定性劣化，加剧了下覆危岩的危险性。如何有效评价爆破动力对危岩体稳定性的影响对于危岩体优化设计及合理治理具有积极作用。但危岩体动力稳定性计算方面目前研究较少，仅有何思明等[8]基于天然危岩体的宏观结构特征，从岩石断裂力学的角度入手，对比分析了不同地震波模式下裂缝的失稳扩展条件，确立了拉剪破坏的危岩失稳机制。其动力崩塌机制及破坏机理还有待进一步研究。

时程分析法指由结构或岩土体沿时间历程进行求解结构或岩土体振动响应的方法，是研究动力问题常用方法之一。相关学者对此作了一定的研究，如徐洪涛等[9]结合刚体极限平衡分析方法中的Sarma方法分析岩质边坡的爆破动力稳定性系数时程，为优化边坡爆破开挖设计提供依据；郑颖人等[10]根据动力分析得到的边坡在地震作用下的破坏机制和破裂面的性质和位置，提出基于拉剪破坏动力时程分析法，改进了动力有限元时程分析法。本文基于危岩体稳定性计算的极限平衡方法和动力时程分析法，针对危岩体清除爆破，建立了滑塌式危岩动力计算模型，通过对爆破荷载衰减分析，提出滑塌式危岩体清除过程中的动力荷载的简化等效方法，将得出的等效爆破动荷载作用于危岩体，得出危岩稳定性系数时程曲线，并结合望霞W2-1危岩体分析验证其正确性，可为危岩动力稳定性计算评价及优化危岩爆破清除设计提供理论依据。

1 时程法分析滑塌式危岩动力稳定性原理

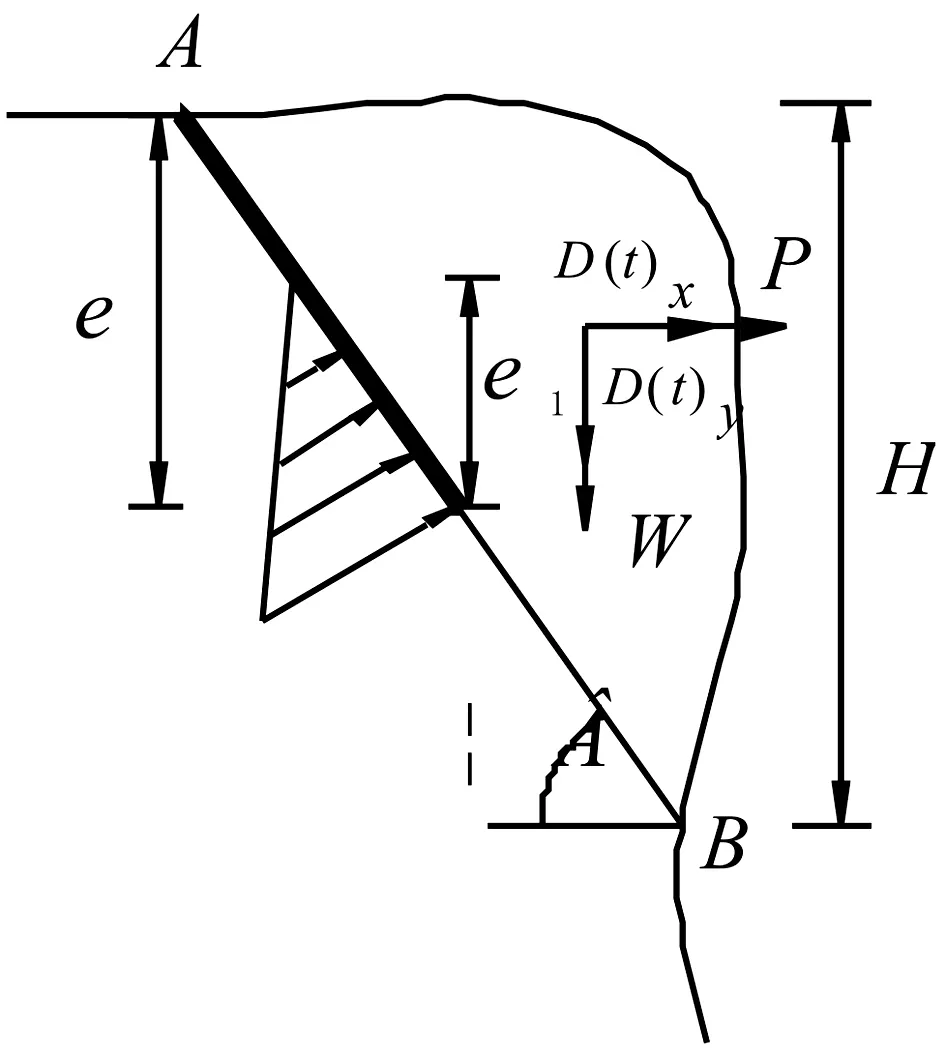
图1 滑塌式危岩动力计算模型

滑塌式危岩动力计算模型见图1，图中AB为主控结构面长度(m)，其倾角为β(°)，等效强度参数为c、φ。W为危岩体自重(kN)，D(t)x和D(t)y为水平和竖直等效爆破荷载，P为水平地震力(kN)。沿主控结构面分解得

法向分量

N=(W+D(t)y)cosβ-(P+D(t)x)sinβ

(1)

切向分量

T=(W+D(t)y)sinβ+(P+D(t)x)cosβ

(2)

假定法向分量和切向分量沿主控结构面均匀分布，则平均法向应力和平均剪应力分别为

σ=Nsinβ/H

(3)

τ=τcosθ/H

(4)

进而可得到主控结构面的抗剪强度为

τf=c+σtanφ

(5)

危岩的稳定性系数为

(6)

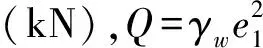
式(6)中D(t)x和D(t)y是随时间t不断变化的，因此在危岩体清除爆破过程中稳定性系数Fs亦随时间波动，并不是一定值，通过对爆破荷载D(t)x和D(t)y的确定，进而可得到滑塌式危岩的稳定性系数时程曲线。

2 危岩体爆破动力的确定

2.1 危岩体内任一质点的爆破动应力计算

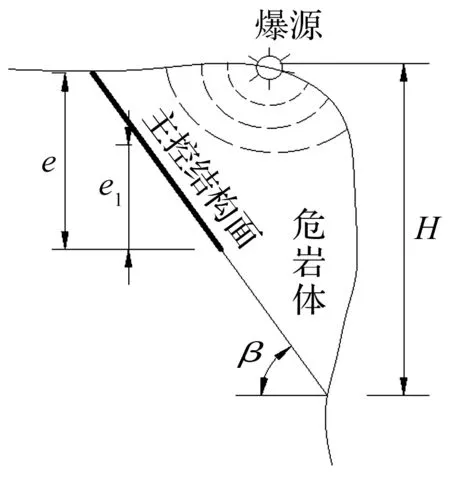
图2 滑塌式危岩动力物理模型

图2为滑塌式危岩动力物理模型图，图中H为危岩体高度(m)；e为主控结构面高度(m)；e1为主控结构面内充水高度(m)；β为主控结构面角度(°)。危岩体清除过程中先在危岩体表层打孔装药，清除表层后爆破工作依次向下进行，直至危岩体清除完毕，因此爆源处在危岩体表层范围内。炸药起爆后首先在危岩体表层形成冲击波致使岩体破碎，后经能量衰减成应力波、地震波在危岩体内传播，因此危岩体受爆破震动波的影响其稳定性将发生变化。假设应力波传递到危岩体某质点处为一维应力波，则由欧拉方程得危岩体内任一质点的峰值应力[12]

σmax=ρ·C·Vmax

(7)

式中，Vmax=K(Q1/3/R)α[2]；σmax为危岩体内任一位置处的峰值应力(MPa)；Vmax为介质质点振动速度峰值(cm/s)；Q为单响炸药量(kg)，齐发爆破为总药量, 延时爆破为最大一段药量；R为爆心距(m) , 指爆破点到介质质点的距离；ρ为介质密度(kg/m3)；C为应力波波速(m/s)；K、α分别为与爆破点至介质质点间的地形、地质条件有关的系数和衰减指数，若无现场监测数据，取值可参考表1[13]。

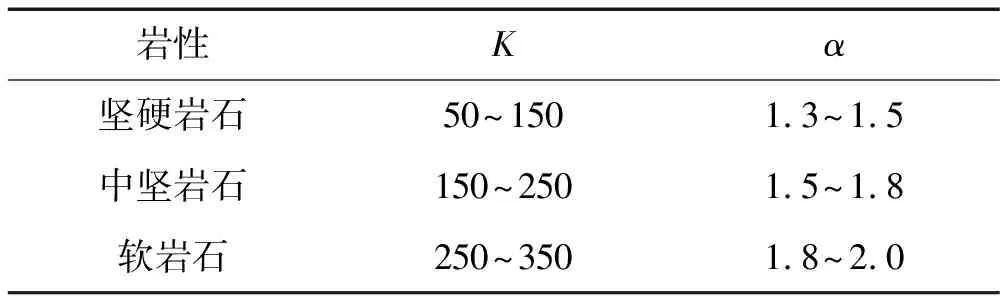
表1 爆破区不同岩性的K、α参考值

2.2 爆破动应力等效简化方法

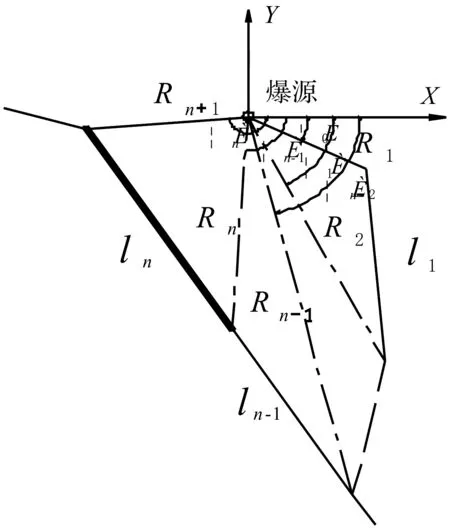
图3 滑塌式危岩简化模型

由式(7)可确定危岩体内任一质点的爆破应力，为了便于计算，将危岩体内所有质点的应力简化到危岩体重心处，由于危岩体自由边界是一不规则形状，难以得到其形状变化的函数，爆破应力难以简化。为得到等效简化的爆破应力，建立滑塌式危岩简化模型(如图3)，简化模型考虑危岩体由n个三角形组成，连接爆源和边界上各个节点，以爆源为发射点向危岩体边界散射，爆源点对应的三角形边长依次为l1、l2、l3、…、ln-1、ln，组成三角形其他两边依次为R1、R2、R3、…Rn-1、Rn、Rn+1，即爆源到边界各节点的爆心距。以爆源为坐标原点，水平方向为X轴，竖直方向为Y轴，连线R1、R2、R3、… 、Rn-1、Rn、Rn+1与X轴的夹角依次为θ0、θ1、θ2、…、θn-1、θn，则线段li对应的直线函数为

y=kix+bi

(8)

将式(8)化为极坐标方程得

(9)

式中，bi、ki由坐标(Ricosθi-1,Risinθi-1)、(Ri+1cosθI,Ri+1sinθi)带入直线方程(8)确定，θ为任一连线与X轴的夹角。

将危岩体内所有质点上的动应力σmax简化到重心处得到水平等效集中力Dx和竖直等效集中力Dy为

水平方向等效集中力Dx

(10)

竖直方向等效集中力Dy

(11)

由于滑塌式危岩无转动效应，简化弯矩M=0。

2.3 危岩体爆破动荷载确定

由式(7)可知，式(10)、(11)得到的等效集中力是峰值集中荷载，并且与时间无直接关系，而爆破应力波是随着时间不断波动的，为了反映危岩体真实动力稳定性情况，假设爆破动荷载D(t)围绕着峰值集中荷载Dmax变化,可表示为

D(t)=Dmaxsin(wt+θ)

(12)

式中:f是频率，θ是初相位角，w=2πf，为角频率。

又由于爆破应力波在传播过程中不仅随距离衰减，还随着时间衰减，因此对上式进行修正得随时间变化的等效爆破动荷载

D(t)=Dmaxe-ψtsin(2πft+θ)

(13)

式中，ψ是时间衰减指数。

将D(t)分解到水平和竖直方向得到水平和竖直等效爆破荷载D(t)x和D(t)y，将得到的等效爆破荷载带入式(6)即可计算出危岩体稳定性系数随时间变化的时程曲线。

3 算例分析——以望霞W2-1危岩体为例

3.1 望霞危岩体概况

重庆市巫山县望霞危岩发育于坡顶陡崖部位，变形区域的危岩以西侧冲沟为界，东至狮子挂银牌西侧，属大型高位危岩，危岩下方为同心村居民区及长江航道。危岩陡壁顶高程1 220～1 230 m，坡脚陡岩底部高程1 137～1 147 m左右，相对高差约70～75 m，分布长度约120 m，平均厚约30～35 m，危岩体总体积约40×104m3。该危岩根据现有结构面及变形情况可分W1、W2-1、W2-2以及楔形体，其中W2-1危岩体(如图4)下覆基座为软岩，基座靠临空面一侧已发生局部压剪破坏，并推挤崖脚公路路基，在上部岩体的自重作用下，基座塑性变形进一步积累，最终发生基座压剪、危岩体滑移失稳。危岩体几何特征及力学参数见表2。由于方量较大，其滑移失稳以平行于临空面的裂隙为边界，呈累进式破坏。望霞危岩工程设计时对W2-1进行削顶减载，采用台阶浅孔爆破，炮孔口径45 mm，深度3 m内，台阶高度2.5 m，因此爆破动力会对危岩体作用，可能导致危岩体稳定性变化。

图4 W2-1危岩体

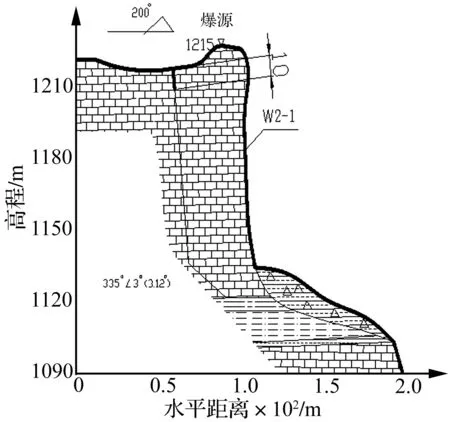
图5 W2-1危岩体剖面图

表2 W2-1危岩体几何及力学参数

3.2 望霞W2-1危岩体动力稳定性计算及时程分析

如图5为W2-1危岩体倾向200°方向剖面图，爆源中心在高程1 215 m爆破台阶上，经危岩体削顶减载现场监测数据[14]，单响药量Q=91 kg，衰减参数K=254.6，α=2.038，时间衰减指数暂无检测数据，取η=10。将表2参数及爆破参数带入式(13)作危岩稳定性系数变化曲线，如图6所示。

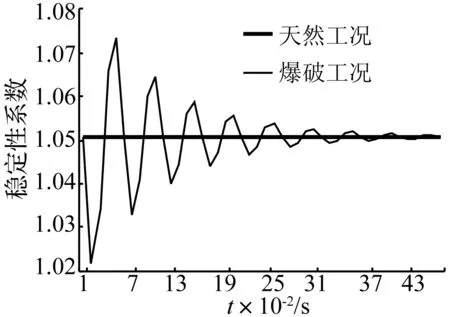
图6 W2-1危岩体动稳定性系数变化曲线

图6为W2-1危岩体动稳定性系数随时间变化的时程曲线，天然状态下危岩稳定性系数Fs=1.05，爆破清除过程中危岩稳定性系数随时间不断波动，随着应力波能量不断衰减，爆破动力对滑体的作用减弱，从图6中可以看出稳定性系数变化峰值幅度随时间逐渐减小，总体趋向于天然工况下的稳定性系数，在0.45 s左右爆破动力对危岩体的作用消失；爆破动力作用下W2-1危岩体最小稳定性系数为1.02，相对天然工况降低了2.86%，随着爆破的进行作用周期加长，加剧了危岩体的危险性。

4 结 论

(1) 根据爆破峰值速度衰减规律及危岩体几何特征，建立了滑塌式危岩动力物理模型及动力计算模型，提出一种简化方法确定了爆破等效荷载，并对等效荷载进行修正，结合极限平衡方法及动力时程分析法最终建立了滑塌式危岩动力计算方法。

(2) 以重庆市望霞W2-1危岩体为例，分析结果表明，爆破清除过程中危岩稳定性系数随时间不断波动，总体趋向于天然工况下的稳定性系数；爆破动力作用下W2-1危岩体最小稳定性系数为1.02，降低了2.86%；爆破对危岩体的作用时间在0.45 s左右，与现场监测数据基本吻合，可为危岩动力稳定性计算评价及优化危岩爆破清除设计提供理论依据。

[1]Chen Hong-kai, Tang Hong-mei, Ye Si-qiao. Damage model of control fissure in perilous rock [J]. Applied Mathematics and Mechanics,2006,27(3):967-974.

[2]陈洪凯,唐红梅,王林峰,等.危岩崩塌演化理论及应用[M]. 北京:科学出版社,2009.

[3]重庆市地方标准,地质灾害防治工程勘察规范[S]. DB50/143-2003:20-30.

[4]陈洪凯,鲜学福,唐红梅,等.危岩稳定性分析方法[J]. 应用力学学报,2009,26(2):278-282.

CHEN Hong-kai, XIAN Xue-fu, TANG Hong-mei, et al. Analysis method of stability for unstable rock[J]. Chinese Journal of Applied Mechanics,2009,26(2): 278-282.

[5]陈洪凯,张瑞刚,唐红梅,等.压剪型危岩破坏弹冲动力参数研究[J]. 振动与冲击,2012,31(24):30-34.

CHEN Hong-kai, ZHANG Rui-gang, TANG Hong-mei, et al. Elastic & impulsive dynamic parameters of a ruptured compression-shear perilous rock[J]. Journal of Vibration and Shock, 2012,31(24):30-34.

[6]陈洪凯,鲜学福,唐红梅,等.危岩稳定性断裂力学计算方法[J]. 重庆大学学报,2009,32(4):434-452.

CHEN Hong-kai, XIAN Xue-fu, TANG Hong-mei, et al. Stability analysis method for unstable rock by fracture mechanics[J]. Journal of Chongqing University, 2009,32(4): 434-452.

[7]陈洪凯,唐红梅,叶四桥,等.危岩防治原理[M]. 北京:地震出版社,2006.

[8]何思明,吴永,李新坡.强震荷载下裂缝岩体拉剪破坏机理[J]. 工程力学,2012,29(4):178-184.

HE Si-ming, WU Yong, LI Xin-po, et al. Failure mechanism of unstable rock under seismic tension-shear action[J]. Engineering Mechanics,2012,29(4):178-184.

[9]徐红涛,卢文波,周创兵,等.基于时程分析的岩质高边坡开挖爆破动力稳定性计算方法[J]. 岩石力学与工程学报,2006,25(11):2213-2219.

XU Hong-tao, LU Wen-bo, ZHOU Chuang-bing, et al. Time history analysis method for evaluating dynamic stability of high rock slope under excavation blasting[J]. Chinese Journal of Rock Mechanics and Engineering, 2006,25(11):2213 -2219.

[10]郑颖人,叶海林,黄润秋,等.边坡地震稳定性分析探讨[J]. 地震工程与工程震动,2010,30(2):173-180.

ZHENG Ying-ren, YE Huang-lin, HUANG Run-qiu, et al. Study on the seismic stability analysis of a slope[J]. Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(2):173-180.

[11]重庆市地方标准,地质灾害防治工程设计规范[S]. DB50/5029-2004:25-27.

[12]王迪安.一维应力波理论在爆破地震效应研究中的应用[J]. 矿业研究与开发,1997,17(1):59-63.

WANG Di-an. An application of theory of one dimension stress wave in study on seismic effect from blasting [J]. Mining Research and Development,1997,17(1):59-63.

[13]水工建筑物地下开挖工程施工规范[S]. SL378-2007: 82-83.

[14]苗高建,周传波,张志华,等.三峡库区望霞危岩体削方爆破振动测试分析[J]. 爆破,2012,29(3):131-134.

MIAO Gao-jian, ZHOU Chuan-bo, ZHANG Zhi-hua, et al. Vibration measurement and analysis of Wangxia unstable rock mass blasting in three gorges reservoir[J]. Blasting, 2012,29(3): 131-134.