层状岩石倾角对弹性模量的影响研究

王金亮

(中铁十一局集团有限公司，湖北 武汉 430061)

0 引 言

岩体的结构特征对岩体在一定荷载条件下的变形破坏方式和强度特征起着关键的控制作用，岩体中的结构面通常成为决定岩体稳定性的控制面。对于层状岩石，其结构面结构非常明显，而且常与其他岩性岩体互层，形成具有互层结构的复合岩体，这种互层复合岩体具有整体各向异性和单一层理内横观各向同性等特征。

复合岩体与单一岩性岩体的变形和强度等性质具有明显差异，国内外许多研究者对复合层状岩体的性质作了大量的研究。谭学术等[1]研究了脆性复合岩体的变形和视在弹性模量，但未研究层理倾角对复合岩体弹性模量的影响；曾纪全等[2]研究了泥质粉砂岩、泥质灰岩抗剪强度参数的层理面倾角效应并用石膏试样进行了验证，阐明了层状、似层状结构岩体力学性质各向异性的本质和机理。苏志敏等[3]在分析大量试验数据的基础上，探讨了页岩的层状结构面倾角和围压对其强度的影响。通过以上研究可知，层状岩体的性质具有显著的倾角效应，随着层理倾角的变化而变化。本文主要研究互层复合岩体层理倾角对岩体的弹性模量的影响，推导互层复合岩体任意层理倾角下在应力加载方向上弹性模量的解析解，并通过不同层理倾角的页岩的单轴抗压实验进行验证。

1 水平状互层复合岩体的变形分析

假设长方体复合岩体由n个各向同性的层状岩体组成，l为长方体高度，a为底边长度，li为第i层的厚度，σ1为岩体所受轴向应力，σ2i、σ3i分别为岩体所受水平应力，那么第i层岩石在三轴应力状态下的应变为：

(1)

其中，Ei、μi分别为第i层岩体的弹性模量和泊松比。

第i层岩石的垂直变形量为：

(2)

那么，互层复合岩体在垂直方向的变形量为：

(3)

2 水平状互层复合岩体弹性模量

2.1 互层复合岩体垂直方向的弹性模量

设水平状互层复合岩体垂直方向的总应变为εV，垂直方向弹性模量为EV，那么，

(4)

如果不考虑围压，即：σ2i=σ3i=0，可得：

(5)

则：

(6)

2.2 互层复合岩体水平方向的弹性模量

复合岩体各层岩体平行于层理面方向的应变相等，由于各层岩石的弹性模量不同，所以各层岩体平行于层理面方向所受的应力不等，各层岩体在水平方向所受的压力之和等于复合岩体所受的总压力[4]，即：

(7)

设互层复合岩体平行于层理面方向的应变为ε2h，弹性模量为Eh，那么，

(8)

(9)

由于公式(9)的各个分项都是大于0的，所以Eh-EV>0，即Eh>EV，也就是说水平状互层复合岩体的平行于层理方向的弹性模量大于垂直于层理方向的弹性模量。

2.3 互层复合岩体的剪切模量

设复合岩体的剪切模量为GV，剪应力为τh，剪切变形为γh，各层岩体的剪切模量分别为G1、G2…Gn，各层岩体的在竖直方向上所受剪应力分别为τ1、τ2…τn，显然τ1=τ2=…=τn，对应的剪应变分别为γ1、γ2…γn，那么各层岩体的剪应力之和等于复合岩体的剪应力：

(10)

(11)

对于复合岩体，剪应力为：

(12)

根据公式(11)和(12)可以推出复合岩体剪切模量和各层岩体剪切模量的关系：

(13)

2.4 互层复合岩体各方向的泊松比

当复合岩体受力情况为σ1≠0,σ2=σ3=0时，σ1(σh)对复合岩体所做的功为：

(14)

当复合岩体受力情况为σ2≠0,σ1=σ3=0时，σ2(σV)对复合岩体所做的功为：

(15)

根据公式(14)和(15)，令Vh=VV，那么：

(16)

公式(16)为水平状互层复合岩体水平方向的泊松比μh与垂直方向的泊松比μV的关系。

3 层理倾角与复合岩体弹性模量的关系

上述得到了层理面水平状态时，互层复合岩体弹性模量与各层岩体弹性模量的关系，将坐标系和所受应力方向绕x轴旋转θ角度(0(°)≤θ≤90(°))，如图1所示，可以推导出互层复合岩体在任意倾角θ度时岩体的弹性模量[5]。

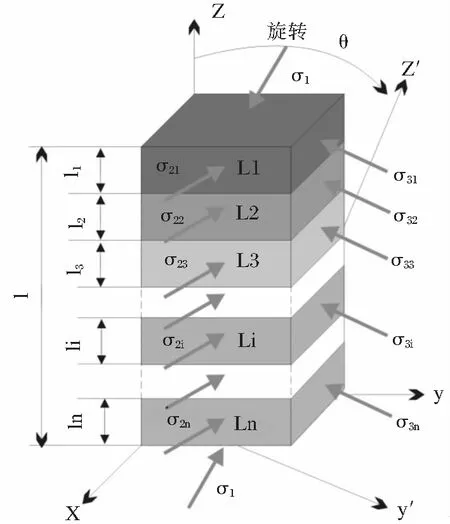
图1 坐标系旋转图

旋转后的坐标系与原来的坐标系有如下关系：

(17)

3.1 坐标轴旋转后应力之间的关系

根据柯西方程可得复合岩体坐标轴旋转后的应力与旋转之前的应力有如下关系：

σ′=dσαT

(18)

将公式展开即为：

(19)

那么，

(20)

写成矩阵形成为：

(21)

即：

[σ]y′z′=R[σ]yz

(22)

3.2 坐标轴旋转后应变之间的关系

根据4.1的思路可得复合岩体坐标轴旋转后的应变与旋转之前的应变有如下关系：

[ε]y′z′=R[ε]yz

(23)

其中，R与公式(22)中R相同。

3.3 互层复合岩体的层理角度与弹性模量的关系

在原坐标系中，互层复合岩体的本构关系为：

[ε]yz=E[σ]yz

(24)

在新坐标系中互层复合岩体的本构关系为：

[ε]y′z′=E′[σ]y′z′

(25)

其中，E′为新坐标系中的弹性模量矩阵。

根据以上公式可得：

R[ε]yz=[ε]y′z′=E′[σ]y′z′=E′R[σ]yz

[ε]yz=R-1E′R[σ]yz

(26)

比较公式(26)和(24)可得：

E=R-1E′R

E′=RER-1

(27)

[ε]y′z′=RER-1[σ]y′z′

(28)

那么，

(29)

E′=

整理得：

(30)

对公式(30)求导，并令其等于0，整理得：

(31)

通过公式(31)可以确定复合岩体弹性模量最小时的层理倾角，由于Eh>EV，所以公式(31)中根号内的分子小于分母，那么θ<45(°)。

4 实验验证

实验页岩样品采自兰渝高铁新城子隧道页岩岩心，在3个不同的露头分别取样，弄清层理方向，每个露头的页岩分别制成层理倾角为0(°)、15(°)、30(°)、45(°)、60(°)、75(°)、90(°)的直径为50 mm、长度为100 mm的标准试样。采用美国GCTS公司生产的高压岩石三轴动态测试系统进行单轴抗压实验，实验测得各个不同层理倾角的3个试验样品平均弹性模量、平均泊松比和平均抗压强度如表1所示。

表1 实验结果

由实验数据可以作出层理倾角与弹性模量的关系图，见图2，可见实验所得曲线与公式推导所得曲线基本吻合，从而证明页岩层理倾角与弹性模量关系公式推导的正确性。

图2 层理倾角与弹性模量关系

当层理倾角为0(°)时，复合岩体弹性模量受层状岩体中最软的那层控制；当层理倾角为90(°)时，复合岩体弹性模量受层状岩体中最硬的那层控制；当层理倾角接近于均值岩体的理论破裂面角度时，复合岩体弹性模量受层状岩体层理面控制。

5 结 论

本文推导了不同层理倾角的互层复合岩体综合弹性模量与各层岩体弹性模量的关系，并通过实验验证了此关系的正确性，得到如下结论：不同层理倾角互层复合岩体的综合弹性模量与层理倾角θ的关系为：

通过采集互层岩体岩心试样进行单轴抗压试验验证了页岩层理倾角与弹性模量关系的正确性。当层理倾角为0(°)时，复合岩体弹性模量受层状岩体中最软的那层控制；当层理倾角为90(°)时，复合岩体弹性模量受层状岩体中最硬的那层控制；当层理倾角接近于均值岩体的理论破裂面角度时，复合岩体弹性模量受层状岩体层理面控制。

[1] 谭学术, 鲜学福. 复合层状岩体的变形及视在弹性模量[J]. 河北煤炭, 1985(1): 27-33.

[2] 曾纪全, 杨宗才. 岩体抗剪强度参数的结构面倾角效应[J]. 岩石力学与工程学报, 2004, 23(20): 3418-3425.

[3] 苏志敏, 江春雷, M Ghafoor. 页岩强度准则的一种模式[J]. 岩土工程学报, 1999, 21(3): 311-314.

[4] 刘立, 梁伟, 李月, 等. 岩体层面力学特性对层状复合岩体的影响[J]. 采矿与安全工程学报, 2006, 23(2): 187-191.

[5] 许丹. 超大吨位基桩静载试验加载时对桩周土的影响范围[J]. 中国锰业, 2017, 35(2): 194-196.