基于HHT研究房屋结构对爆炸地震的振动响应

曾一鑫，白春华，王仲琦

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

现阶段国内大型油气田开发多采用炸药作为地震勘探的震源。随着勘探精度的提高，为了获得完整的地震资料，炸药震源时常被埋放在离村庄、城镇仅几十米的位置。由此给房屋结构带来的振动危害是不可忽视的。房屋结构对爆炸地震的振动响应有着重要的研究价值。许多国家对于房屋结构的振动都建立了相应的标准[1-3],这些标准有一个共同点：对不同频率的振动幅度有不同的允许阈值。Siskind[4-6]通过监测采矿爆破周围的房屋振动发现，在接近房屋结构固有频率的频段内，房屋结构上的振动相对于临近其地基的地面振动有不同程度的放大。Pijush[7]指出结构的振动响应取决于地表介质的动力学特性和房屋结构的建造类型及自振特性。林键等[8]对3-4层房屋结构的爆破振动响应进行了测试，发现随着楼层的增加，振动速度峰值(PPV)会不同程度的增加。上述研究都是在采矿爆破的大前提下形成的，炸药药量通常在几百公斤以上，且爆炸的位置距离房屋结构在几公里外。而作为地震探勘用的炸药震源药量通常小于10 kg，炸药距离房屋较近，对于这类情况下房屋结构的振动响应研究较少。此外，研究抗震性能好的房屋结构和开发减震材料是建筑学者始终关心的课题[9]。碳纤维板加固技术对于房屋结果的减震效果是十分显著的[10-11],对爆炸地震效应的减震效果的研究还较少。

基于上述原因，对一新建的二层钢筋混凝土-水泥砖墙的房屋结构进行爆炸振动测试试验，利用希尔伯特-黄变换(HHT)[12-13]对房屋结构上不同位置出的振动信号进行频谱分析。获得了房屋结构的对爆炸地表振动的响应特性，同时对比研究了碳纤维板加固对建筑结构的减振效果。

1 振动测试试验

1.1 试验现场条件

二层钢筋混凝土-水泥砖墙房屋结构建在平坦空旷的砂质土上，如图1。炸药选用TNT，药量为10 kg，炸药埋覆于距离房屋结构20 m，30 m与40 m的土中，深度为2 m。试验顺序是从40m处到20m处，目的是为了防止爆炸后砂土成坑造成下一次试验产生较大的误差。临近房屋结构地基的地面上振动速度的测试系统选用美国劳雷公司的NZXP24型高精度地震仪，该仪器测试动态范围为144 dB。而在房屋结构上的振动测试选择加速度传感器(国内702所生产)，量程为10 g，灵敏度为24 PC/g，每个加速度传感器外均附加钢制的保护壳。传感器的位置如图2所示，将墙上的加速度传感器命名为W1-W4，将钢筋混凝土柱上的加速度传感器命名为P1，将贴近房屋地基地面上的速度传感器命名为G1。需要重点说明的是：图2中右侧的墙W2和W4是通过碳纤维板加固的墙，而W1和W3是普通的砖墙。

图1 二层水泥砖墙房屋结构图

图2 传感器位置及编号

1.2 振动幅值特性

房屋结构上振动信号的峰值振动速度与响应的地面G1的峰值振动速度如表1所示。可以看到，房屋结构上的振动速度峰值相对于G1来说有不同程度的放大效果。

表1 峰值振动速度(mm/s)

2 振动信号分析

2.1 希尔伯特-黄变换(HHT)

傅里叶变换(FT)和小波分析(Wavelet)一直是运用最广泛的分析手段[14-15]。但二者有一个共同的缺陷：必须预先设定的先验基底函数。希尔伯特-黄变换(HHT)是近些年来信号分析研究领域的一个重大突破，相对比FT和Wavelet，HHT是一种自适应的分析方法，不需要先验基底函数[12-13]；对信号的处理有更强的局部特性，能更好地表征信号的强间断特性。尤其对于非线性系统产生的随机非稳态信号处理有很大的优势。HHT的本质是对信号的平稳化处理，主要包括了两大模块：一是对时程信号的经验模态分解(Empirical Mode Decomposition, EMD)，模态分解后的数据序列被称作固有模态函数(Intrinsic Mode Function, IMF)；二是对每个IMF进行Hilbert变换，获取其时间-频率-能量三维特性。

2.2 测试信号的EMD分解

假定原始时程信号S(t)，找到所有极值点，用三次样条曲线分别对极大值点、极小值点进行差值获取信号的上包络线Smax和下包络线Smin。对Smax和Smin求均值得到均值线M1(t)，再用原始信号S(t)减掉M(t)获得第一个IMF分量C1(t)。

(1)

C1(t)=S(t)-M1(t)

(2)

判断C1(t)是否满足IMF函数的两个要求[12]：①C1(t)中的数据极值点数量与曲线穿过零值点的数量相差必须≤1； ②C1(t)中任意数据点由Smax和Smin两条包络线确定的平均值为0。如果C1(t)满足上述条件，则视C1(t)为第一个IMF函数。通常情况下，C1(t)还不能满足上述条件，此时将C1(t)设为原始信号，重复上述算法：

C11(t)=C1(t)-M11(t)

(3)

这类算法有可能进行k次，直到C1k(t)满足IMF函数要求为止，才可以获得信号的第一个IMF函数IMF1(t)：

C1k(t)=C1(k-1)(t)-M1(k-1)(t)

(4)

IMF1(t)=C1k(t)

(5)

这类重复算法有一个终止的判断准则，可以利用两个连续处理结果之间的标准差R的值做判据：

(6)

通常R取值在0.2～0.3。第一个IMF函数产生之后，将从原始信号S(t)中减去IMF1(t)获得的差值再重复上面的算法依次获得余下的IMFi(t) (i=2,3,4…)。

利用上述方法对30 m处的试验时，G1、P1和W1的振动信号进行EMD分解，可以得到如图3-图5所示的结果。需要说明的是P1和W1测到的原始信号为加速度信号，在进行EMD分解之前利用数值积分程序将加速度信号转变为速度信号。每组信号的6个IMF分量IMF1-IMF6，包含了不同的频域特征尺度，随着分解的先后顺序，频率逐渐降低。分量的振幅越大，说明该频率段的信号能量越强。就地面振动信号G1而言，IMF1-IMF3的幅值大，说明在相对较高的频率段内振动能量较高。而对于房屋结构上振动信号，IMF4-IMF6的幅值大，说明在较低的频率段内振动能量较高。此外P1和W1上的振动幅度要高于G1，这个现象说明房屋结构对爆炸产生的地面振动有放大效应，定量的放大倍率和频率特性会在下一节作详细分析。

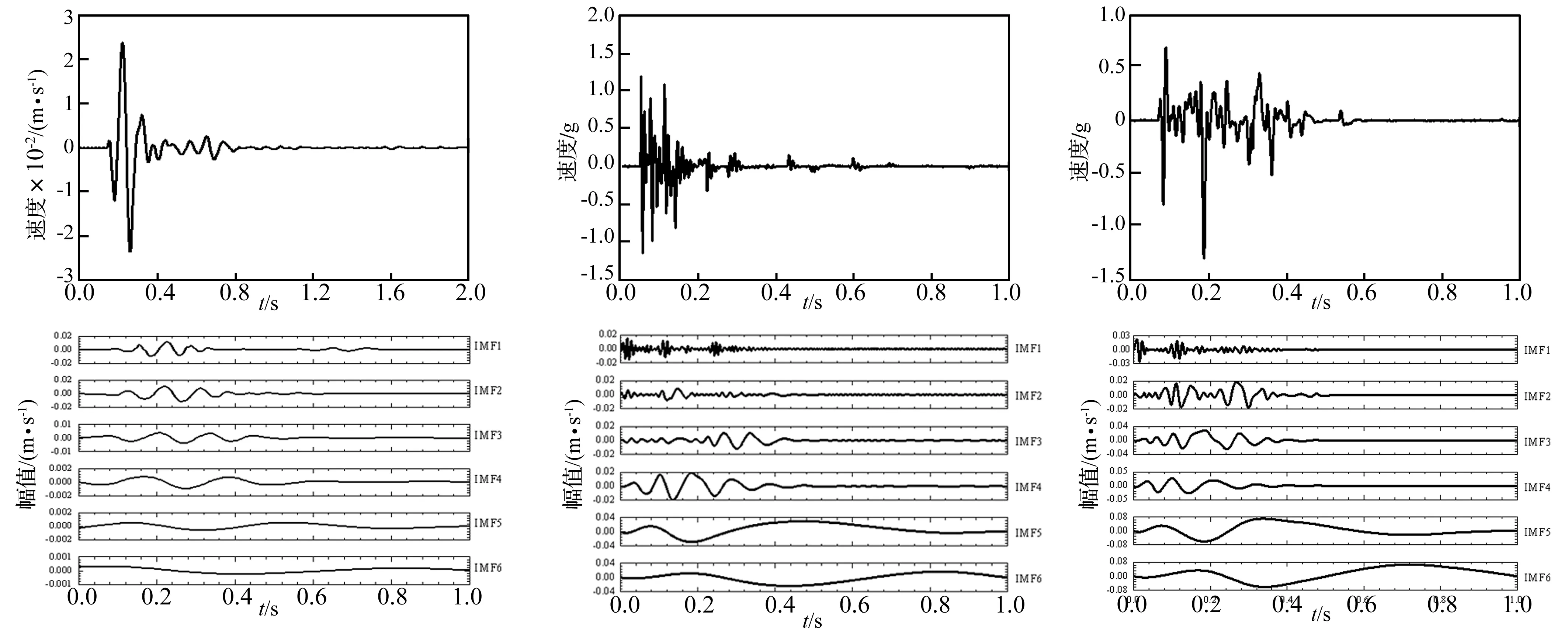
图3 30 m处试验地面振动信号G1及其IMF分量

2.3 振动信号IMF分量的Hilbert频谱分析

应用EMD获取的IMF分量再进行Hilbert变换：

(7)

式中：PV代表柯西主值。运用EMD算法获取的IMF分量IMF(t) 和Hilbert变换获取的变换谱H[S(t)]可以构造解析信号z(t)，该解析信号的幅值a(t)，也称包络幅值，其表达式为：

z(t)=IMF(t) +iH[IMF(t)]=a(t)eiθ(t)

(8)

(9)

Hilbert时频谱的表达式如下：

(10)

通过Hilbert变换还可获得信号的瞬时频率ωin：

(11)

(12)

将房屋结构上振动信号分解出的IMF分量进行Hilbert变换，并求解频率域内与地面G1的比值，如图6与图7。

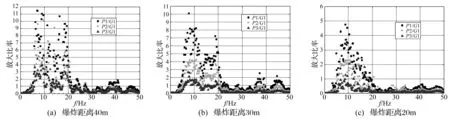
图6 混凝土柱P1-P3振动相对地面G1在频率域内的放大效果

不难发现，钢筋混凝土柱和水泥砖墙，在靠近其固有频率的一段频率域内，振动信号的幅度相对于G1均有明显的放大效果(Amplification Ratio > 1)，炸药爆炸距离从40 m减小到20 m，能产生放大效果的频率段变窄。这个现象产生的主要原因是离炸药近的地面振动频率较高。对于混凝土柱，不同高度处振动相对地面的放大倍率会有明显不同，位置越高其放大倍率越大，P1>P2>P3。随着炸药更加靠近房屋结构，P1，P2和P3在频率域内的振动放大倍率都会降低，峰值放大倍率由11.6，10.1和6分别减小到4.8, 2.4和2.1，但始终维持在8-10 Hz；能够产生放大效应的频率段从6-30 Hz变窄到6-18 Hz。对于墙体的振动，处在第二层的W1和W2相对于G1的放大倍率要大于第一层的W3和W4，进一步说明了房屋结构上位置越高振动幅度越大。随着炸药更加靠近房屋结构，W1,W2,W3和W4在频率域内的峰值放大倍率从12.3, 4.5, 8,2和4.4降低为3.8, 1.6,1.7和1.03。对比相同高度的墙体，可以发现由于W2和W4有碳纤维板的加固，相对于G1的放大倍率要分别远小于相同高度的W1和W3，其中W2约为W1的36.6%-49.8%，W4约为W3的34.1%-53.7%。事实上，在爆炸距离为30 m和20 m时，在第一层的墙体W4相对于G1几乎没有放大，而没有碳纤维板加固的W3还能观测到的放大倍率为4.2和1.7，这体现了碳纤维板有明显的减震效果。值得注意的是，碳纤维板并未改变墙体的固有频率，当炸药爆炸距离从40 m减小到20 m，墙体能产生放大效果的频率段变窄，但出现峰值放大倍率的频率维持在7-12 Hz。普通的水泥砖墙在受到地震作用时，其材料延性差，抗剪切能力低，尤其是构造不规范的房屋在轻微振动下便发生破坏；碳纤维板加固能极大的提高墙体的抗冲击和抗剪切能力。

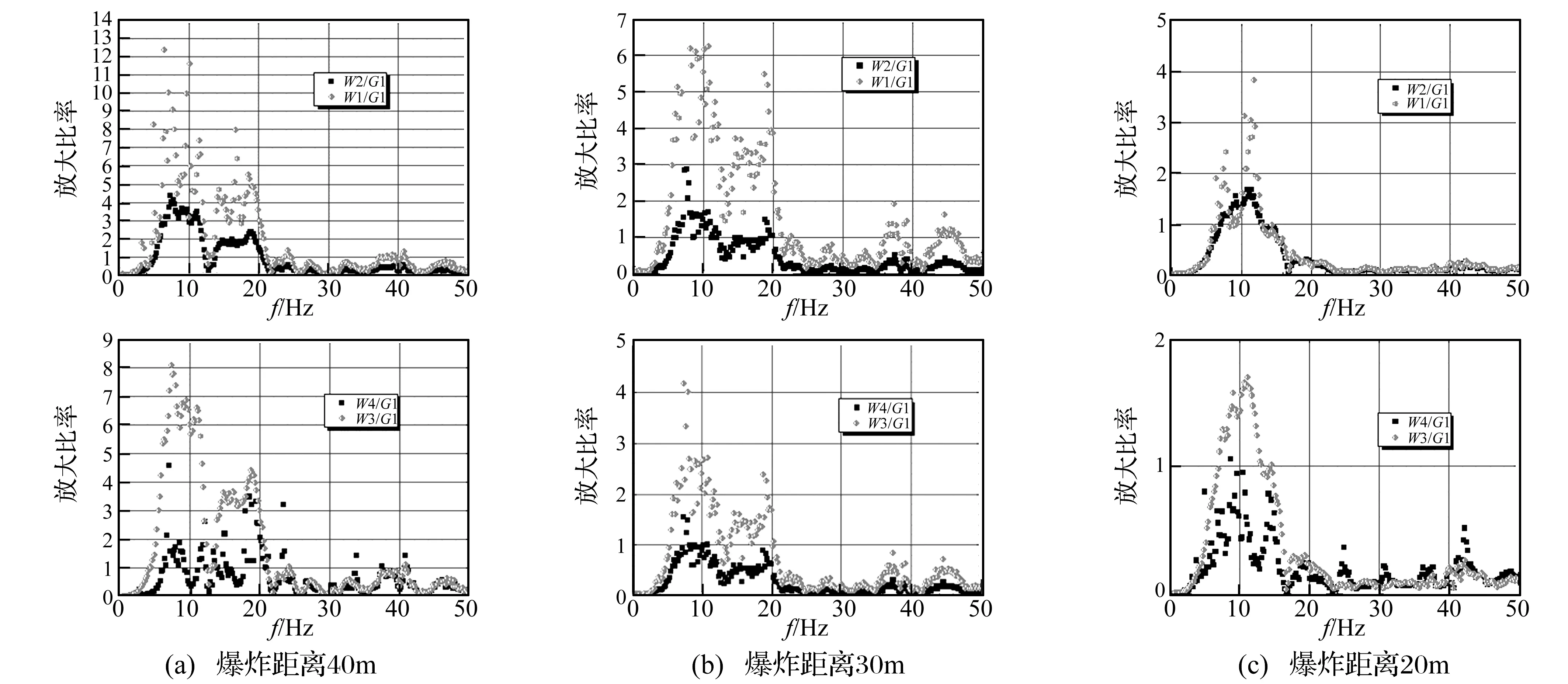
图7 墙体W1-W4振动相对地面G1在频率域内的放大效果

3 结 论

本文对新建的二层钢筋混凝土-砖墙结构进行了爆炸振动响应测试试验，以房屋结构上的振动相对地基附近地面振动的放大倍率为指标，利用HHT分析了房屋结构爆炸振动的频谱响应特征。发现在靠近房屋结构自振频率的频率域内，房屋结构呈现不同程度的振动放大效应。高度较高的位置处，包括钢筋混凝土柱和墙体，它们在域内的峰值放大倍率要高于较低位置。而炸药与房屋结构的距离越小会造成峰值放大倍率的减小以及能够产生放大效应的频带变窄。对比分析了相同高度处经碳纤维板加固后的墙体和普通墙体的振动特性，结果表明碳纤维板加固对爆炸地震效应有明显的减振效果，有碳纤维板加固的墙体振动幅度要低于相同高度普通墙体振动的1/2。

[1]Siskind D E, Stagg M S, Kopp J W, et al. Structure reponse and damage produced by ground vibration from surface mine blasting[R]. US Bur Mines Rep Invest 8507, 1980.

[2]German Institute of Standards. Vibration of building-effects on structures[R]. DIN 4150, 1986,(3).

[3]Singh P K, Roy M P. Standardisation of blast vibration damage threshold for the safety of residential structures in mining areas[R]. Central Mining Research Institute (India), R&D report, 2006.

[4]Siskind D E, Stagg M S, Kopp J W, et al. Structure response and damage produced by ground vibration from surface mine blasting[R]. United States Bureau of Mines, RI 8507. 1980.

[5]Siskind D E, Stachura V J, Nutting M J. Low-Frequency vibration produced by surface mine blasting over abandoned underground mines[R]. United States Bureau of Mines,RI 9078. 1987.

[6]Dowding C H. Blast vibration monitoring and control[R]. Englewood Cliffs, NJ: Prentice-Hall, 1985.

[7]Pijush P R. Characteristics of ground vibrations and structural response to surface and underground blasting[J]. Geotechical and Geological Engineering, 1998, 16: 151-166.

[8]林键, 林从谋, 林丽群. 爆破振动载荷作用下3～4层房屋结构响应测试研究[J]. 振动与冲击, 2010 29(3): 48-66.

LIN Jian, LIN Cong-mou, LIN Li-qun. Test research on structural response to blasting vibration loading of 3～4 layers building [J]. Journal of vibration and shock, 2010 29(3): 48-66.

[9]陈国, 单波, 肖岩. 轻型竹结构房屋抗震性能的试验研究[J]. 振动与冲击, 2011, 39(10): 136-142.

CHEN Guo, SHAN Bo, XIAO Yan. A seismic performance tests for a light glubam house [J]. Journal of vibration and shock, 2011, 39(10): 136-142.

[10]John J. Reinforcing masonry walls with composite materials [D]. Stanford University, 2000.

[11]Attard C K, Mario M. Modeling of unreinforced masonry walls under shear and compression [J]. Engineering structures, 2007, 29(9): 289-296.

[12]Huang N E. Introduction to the Hilbert-Huang Transform and its related mathematical problems[M]. Interdisciplinary mathematics, 2005.

[13]Huang N E, Long S R, Shen Z. The mechanism for frequency downshift in nonlinear wave evolution [J].Advances in applied mechanics. 1996, 32: 59-111.

[14]Grossmann P, Grossmann A, Morlet J. Cycle-octave and related transforms in seismic signal analysis[J]. Geoexploration,1984, 23: 85-102.

[15]林大超, 白春华. 爆炸地震效应[M]. 北京：地质出版社，2007.