驶入式钢货架动力特性试验研究

武振宇，成 博

(哈尔滨工业大学 土木工程学院，哈尔滨 150090)

驶入式钢货架是一种高存储密度的货架，占用仓库空间小，叉车直接驶入货物通道内部存取货物。相对于更常见的横梁式货架，其更适用于存储种类少、数量大的货物。

目前，国内外对货架结构的研究主要集中在货架静力性能上，并形成了设计规范[1-3]，对货架动力性能的研究(尤其是驶入式货架的动力性能)开展得较少[4]。货架设计主要进行静力计算，因而在地震强度不大的情况下，就曾发生了货架倒塌事故。此外叉车在装卸货物时，不可避免会与货架发生碰撞，这也是造成货架倒塌的部分诱因[5]。Gilbert等[6-7]采用原型试验和数值计算的方法研究了叉车撞击驶入式货架的冲击力以及受撞击立柱弯曲变形的大小。Hua等[8]分析了驶入式货架在受叉车碰撞后的反应，其有限元分析模型中的阻尼参数是人为设定的。

为对驶入式货架在地震作用下和冲击作用下的动力性能研究奠定基础，本文使用初始位移法对驶入式钢货架试件进行了自由振动试验，研究了驶入式货架自振频率和阻尼等动力特性。根据试验结果分析了货架的支撑布置形式、货物通道个数和货物等因素对货架动力特性的影响。

1 试验概况

1.1 试件设计与制作

驶入式钢货架需要叉车进入货物通道内存放货物，因此货架立柱的间距较大。为了便于试验，本试验没有采用市场上的货架成品，而是由货架制造厂特别制作了尺寸较小的货架试件。货架试件的构件截面与连接形式均与实际货架相同，此试件的试验结果能够代表典型的驶入式钢货架性能。目前驶入式货架中构件间多采用螺栓连接，因此摩擦阻尼是货架阻尼的主要来源之一。采用扭矩扳手控制螺栓的预拉力，可以调整货架摩擦阻尼的大小，使其满足阻尼的相似条件。

本文根据货架支撑构件布置形式、货物通道个数以及货物存放与否来区别试件类型，每类试件有两个相同的试件。试件的编号规则见图1。如试件Q3WA表示有三个货物通道、设置水平和竖向支撑、没有存储货物的货架，其构造图见图2。为了便于描述，下文使用两个方向的轴线编号(图2中的俯视图)来表示货架立柱。例如将C轴与2轴相交处的立柱命名为立柱C2。

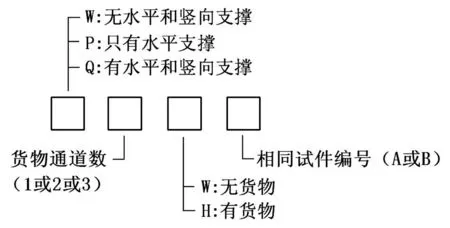
图1 试件编号规则

货架构件为冷弯薄壁轻钢构件，部分构件截面形式见图2。其中，立柱截面为复杂卷边C形截面，并且在其腹板上有规则孔洞，这是为了方便连接横梁等其他构件；横梁为薄壁焊接方钢管，在其两端焊接有连接件；立柱支撑杆为卷边C形截面；牛腿梁为冷弯变形卷边Z形截面，其腹板上会放置货物托盘；支撑(斜拉)为薄钢条，一端连接有张紧器，可施加一些预拉力。在立柱的底端焊接有底板，其通过螺栓与已固定在地面的地梁相连。采用M8或M10的4.8级普通螺栓将货架构件连接在一起，形成整体货架体系。货架构件的截面特性见表1。

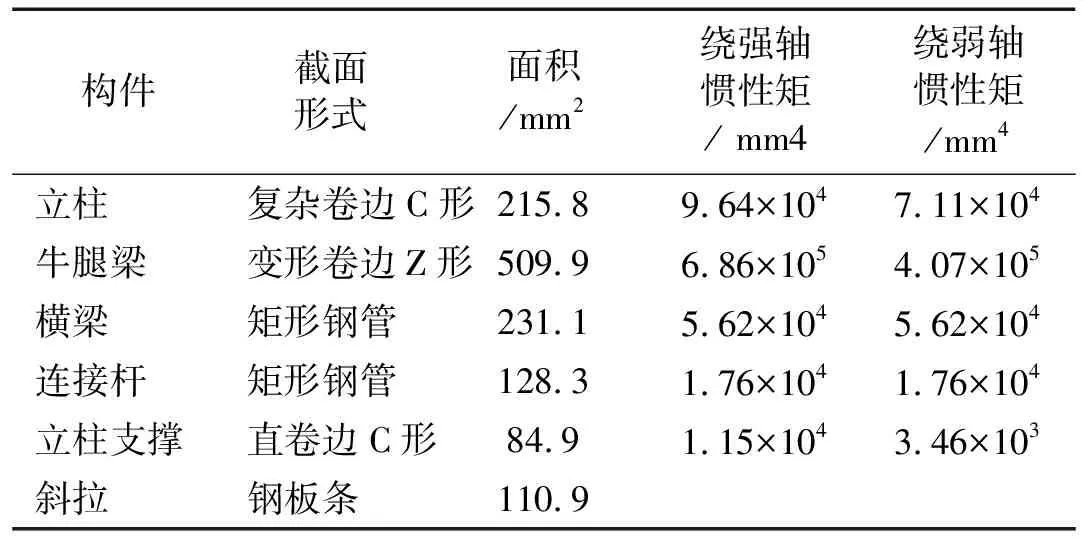
表1 货架构件截面特性

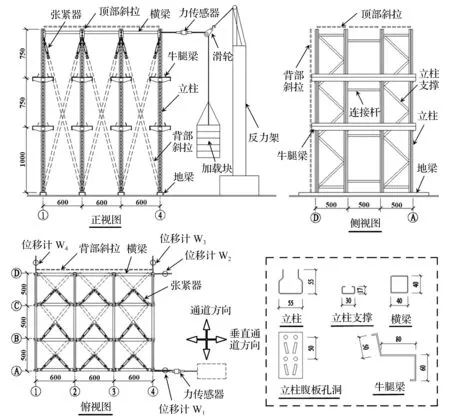
图2 驶入式货架试件Q3WA结构示意图

货架构件在试验过程中，一直处于弹性状态，而且构件之间的连接是可以反复拆装的。因此，货架构件(立柱、横梁、支撑和牛腿梁等)可被重复利用，组装成不同的试件。但是参数相同的两个试件(如W2WA和W2WB)由完全不同的构件组装而成。为了便于叙述，在下文中，将没有设置支撑的试件称为无支撑试件；将只设置水平支撑的试件称为水平支撑试件；将设置有两种支撑(水平和竖向支撑)的试件称为全支撑试件。

1.2 试验方案

本文采用初始位移法对货架施加冲击荷载[9]，进行自由振动试验。货架上承受水平外力的节点位于立柱A4上端的腹板上，高度与横梁的中心线相等(见图2中的正视图和俯视图)。一根连有力传感器的绳索的一端连接在此受力节点上，另一端绕过一个滑轮连接一个重物托盘。在试验时，在重物托盘中放置重物块，向绳索施加一个向下拉力，然后将此力快速卸去，使货架自由振动。每个试件重复三次振动试验。每次试验所施加的荷载有所不同，最大荷载值不大于0.6 kN。

试验采用边长400 mm的正方形建筑木模板模拟货物托盘，采用自重20 kg的铁制重物块模拟货物。每个托盘上放置四个重物块。加载后的货架试件见图3。

图3 重物块加载后的货架

本试验在哈尔滨工业大学结构抗震试验室中完成。试验主要测量柱顶水平位移的自由振动衰减曲线。四个电子位移计LVDT(编号为W1～W4)分别布置在货架试件的角部(见图2中俯视图)。其中，两个位移计(W1和W2)测量立柱A4和D4上端在垂直于通道方向的位移；另外两个位移计(W3和W4)测量立柱上端在通道方向的位移。使用信号测试分析系统DH5922自动采集位移计和力传感器的信号，信号采集频率为50 Hz。

2 试验结果及分析

2.1 自振频率和阻尼比

三个典型的货架试件自由振动位移曲线见图4。图中的Δ1和Δ2分别为位移计W1和W2(见图2中的俯视图)的读数。当货架向右侧移时，两个位移计的读数为正。另外两个位移计W3和W4(平行货物通道方向)的位移较小，这里不再讨论。

图4 一些试件自由振动曲线

由于没有背部竖向支撑，无支撑与水平支撑试件的前部和背部(见图2)是对称的，其第一阶振型应为货架向一侧均匀侧移，货架前部和背部侧移的程度应是一样的。因为只在立柱A4上施加水平力，货架在振动开始前，Δ1和Δ2的振动幅度和相位并不相同。但当货架发生振动后，由于阻尼的存在，非主要振型的振动分量会迅速消失，Δ1和Δ2曲线很快保持同步，货架按照第一阶振型进行振动(见图4(a)和4(b))。

全支撑试件在其背部设置了竖向支撑，因此其货架背部立柱的振动幅度比货架前部立柱小。此类货架第一阶振型的Δ1和Δ2值不同，但是前后立柱的振动也是同步的(见图4(c))。

本文货架的自振频率和阻尼比都是由Δ1曲线的数据得到的。为了避免货架振动开始时的不稳定性，曲线数据的取值是从第二个波峰或波谷开始的(见图4中M点和N点)。从M点和N点起，提取后面数个波峰和波谷对应的时间值，进而可以得到数个周期值。将这些周期的平均值的倒数定义为此试件的自振频率，自振频率的计算结果见表2。表2中的自振频率是每个试件三次振动试验结果的平均值，参数相同的两个试件(如试件W3WA和W3WB)的自振频率基本相同。

对于振动衰减曲线，对数衰减率δ由相隔j个周期的两个位移振幅值的比值确定。假设Ai是某一时刻波峰或波谷的振幅值，Ai+j是j个周期后的振幅值，ζ是结构阻尼比。对数衰减率δ为：

(1)

因为阻尼比ζ一般都很小，所以式(1)可近似为：

δ=ln(Ai/Ai+j)=2jπζ

(2)

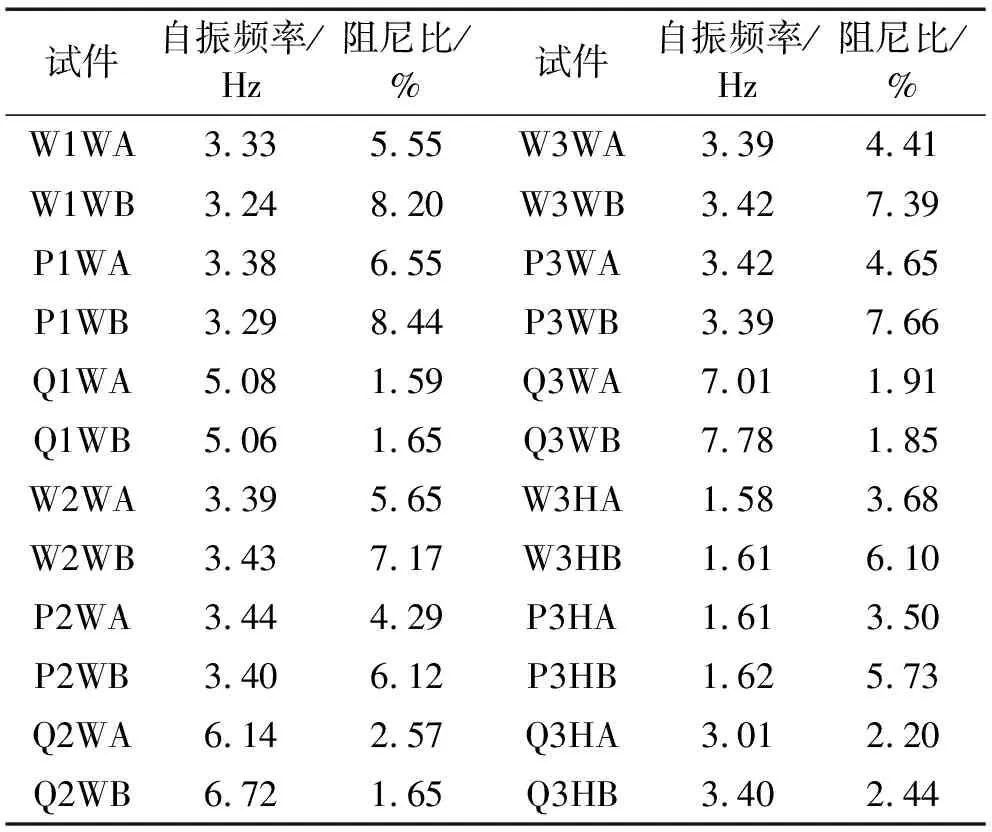
表2 货架自振频率和阻尼比

本文根据波峰振幅值计算试验阻尼比时，将M点(见图4)的振幅值设为Ai，j个周期后的波峰振幅值设为Ai+j，再由式(2)计算得到波峰阻尼比。此外，再由相同的计算过程由波谷振幅值得到波谷阻尼比。将波峰与波谷阻尼比的平均值定义为此试件的阻尼比。阻尼比的计算结果见表2，表中的阻尼比是每个试件三次振动试验结果的平均值。参数相同的两个试件(如试件W3WA和W3WB)的结果差别较大。大多数第二批试件(试件编号尾号为“B”)的阻尼比值比第一批试件(试件编号尾号为“A”)大，这主要与试件的装配过程有关。由于装配熟悉程度不同，两批试件的装配过程不可避免地会有一些差别。

2.2 构造参数对自振频率的影响

当货架按照主要振型振动时，增加水平支撑不会增加其侧向刚度，对试件自振频率的影响不大。然而，设置背部竖向支撑会增加试件的在垂直通道方向上的侧向刚度和自振频率。以无货物的三通道试件为例，其全支撑试件(Q3WA/B)的自振频率平均值比水平支撑试件(P3WA/B)提高了118%。

对于无支撑和水平支撑试件，通道个数增加时，货架侧向刚度和质量同步增加，因此通道个数不会影响试件的自振频率。而对于全支撑试件，货物通道数的增加，会使试件的自振频率增大，这主要归咎于竖向支撑个数增加的幅度比货架质量大。比如，当单通道货架变为双通道货架时，立柱由2列增加到3列，而竖向支撑却由1组增加到2组。全支撑的双通道试件(Q2WA/B)和三通道试件(Q3WA/B)的自振频率平均值分别比单通道试件(Q1WA/B)增大了26.6%和45.8%。

货物的存储会增大整个货架的质量和自由振动周期，即减小试件的自振频率。对于水平支撑试件，有货物的试件(P3HA/B)的自振频率平均值比无货物试件(P3WA/B)减小52.8%；对于全支撑试件，有货物的试件(Q3HA/B)的自振频率比无货物试件(Q3WA/B)减小56.6%。

2.3 构造参数对阻尼比的影响

如表2所示，试件阻尼比结果的离散性较大，规律性也较差。可以确定的规律是：上部水平支撑的设置对试件阻尼比的影响较小，而设置背部竖向支撑能降低试件的阻尼比。背部竖向支撑的设置会减小货架后部的振动幅度，减少此处货架连接节点的变形和摩擦阻尼。全部无支撑和水平支撑试件的阻尼比的平均值为5.94%，而全部全支撑试件的阻尼比的平均值为1.98%。

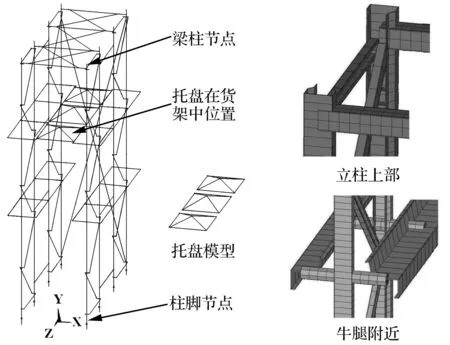
图5 有限元模型

3 有限元模拟

使用有限元计算软件ANSYS对上述货架试件进行模拟，主要构件(如立柱、横梁和牛腿等)采用梁单元BEAM188模拟。有限元模型的示意图见图5。根据构件的实际截面尺寸，有限元梁单元采用了自定义截面形式(见图5右侧细节图)。根据节点试验和分析结果，将立柱上端梁柱节点的绕z轴抗弯刚度确定为18 kN.m/rad，并且分别将无货物和有货物试件的立柱下端柱脚节点绕z轴的抗弯刚度确定为9 kN.m/rad和12 kN.m/rad。支撑构件采用杆单元LINK10进行模拟。参考文献[10]，本文将支撑的截面积进行了折减。货物托盘也采用梁单元模拟(见图5)，其与牛腿梁之间的摩擦作用采用非线性弹簧单元COMBIN39模拟，水平弹簧单元的荷载-变形关系由一个斜率很大的弹性段斜线段和一个水平线段组成。托盘与牛腿梁之间的摩擦系数为0.4，由两者摩擦滑移试验确定。

对货架有限元模型进行模态分析，其基本频率fM的计算结果见表3。由表3可知，数值计算与试验得到的试件自振频率结果吻合较好。

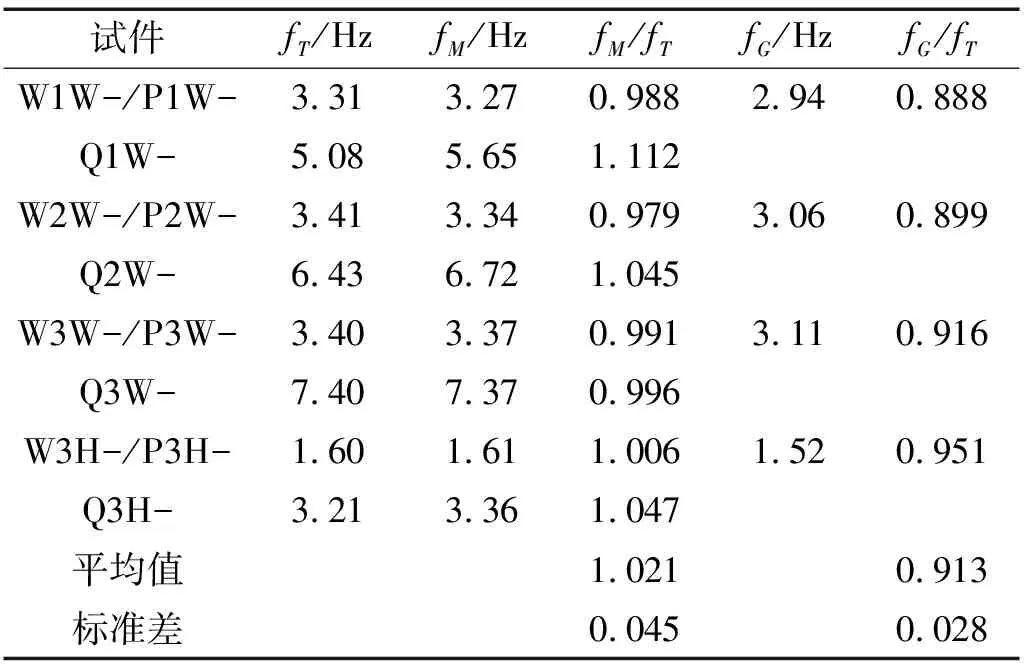
表3 货架自振频率

对货架有限元模型进行瞬态动力分析。本文有限元模型采用结构分析常用的瑞利阻尼[11]，即：

[C]=α[M]+β[K]

(3)

式中，[C]、[M]和[K]分别为结构的阻尼、质量和刚度矩阵。质量阻尼系数α和刚度阻尼系数β可通过振型阻尼比计算得到，即

(4)

(5)

式中，ωi和ωj分别为任意给定的两阶自振频率，ξi和ξj是与之相对应的振型阻尼比。对于式(4)和(5)，可以规定ξi=ξj=ξ，则

α=2ωiωjξ/(ωi+ωj)

(6)

β=2ξ/(ωi+ωj)

(7)

根据前述振动试验得到的试验自振频率，确定合理的频率范围的下限ωi和上限ωj。而ξ则取为试验得到的试验阻尼比。根据式(6)和式(7)计算得到两个阻尼参数α和β，用于有限元动力分析中。

图6为试件P2WB数值计算得到的自由振动Δ1曲线与试验Δ1曲线对比。两个方法得到的振动曲线吻合较好，表明此有限元模型可较好地模拟货架的动力性能。

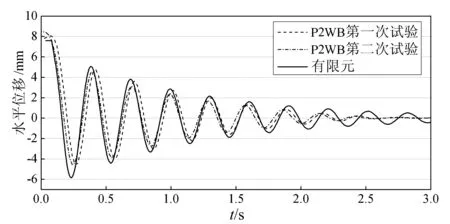
图6 试验和数值计算得到的自由振动Δ1曲线

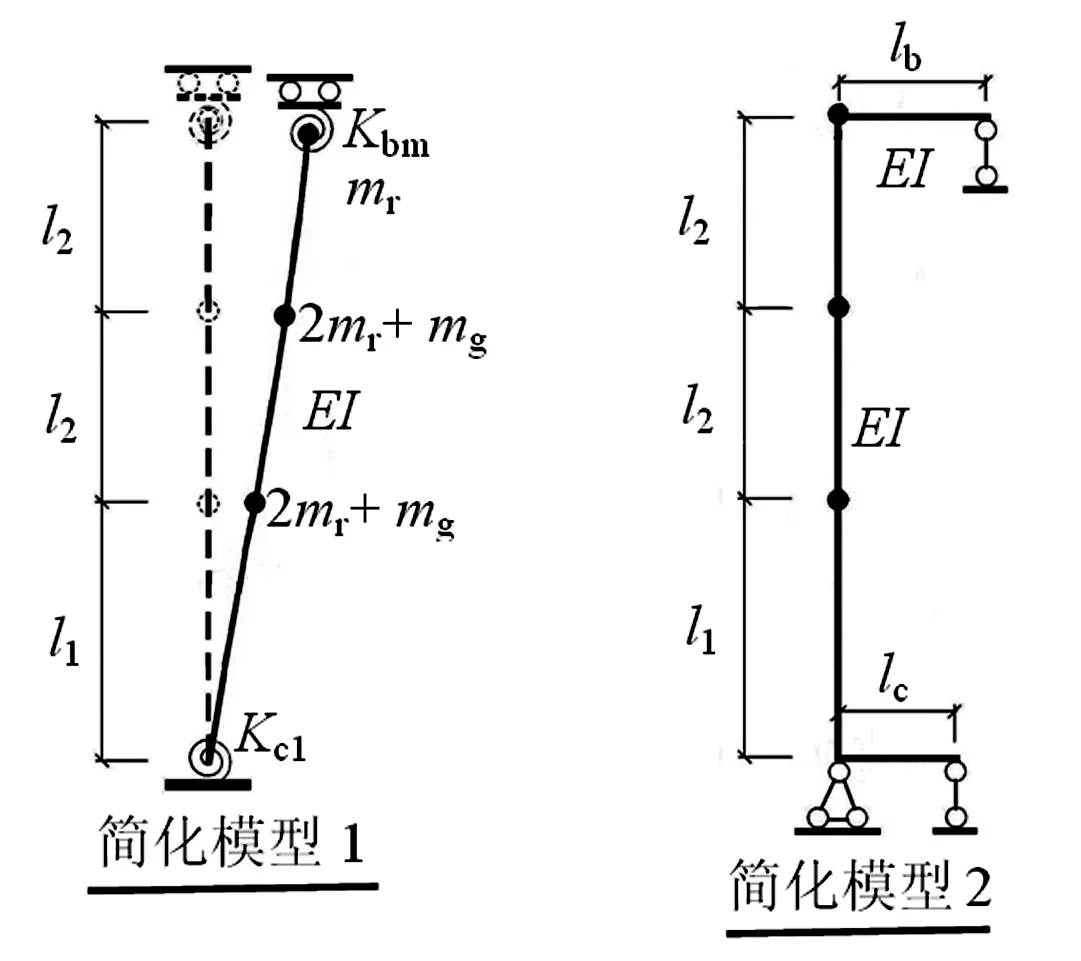
图7 自振频率简化计算模型

4 自振频率简化计算

采用第3节的有限元模型计算货架自振频率比较复杂，本节根据没有设置竖向支撑货架的振型特点，提出了两个计算此类货架自振频率的有限元简化模型(见图7)。在平行于货物通道方向上，立柱被支撑、连接杆和牛腿梁等构件连接起来(见图2)，立柱在绕其截面对称轴弯曲时的扭转受到约束，因此图7中的简化计算模型仅考虑立柱的平面弯曲，立柱使用平面梁单元模拟。平面梁单元只需设置立柱的截面积和绕其对称轴的惯性矩。本试验货架的自重简化为三个集中质量，其中mr为3.8 kg；每层货物平均到每个立柱的重量mg为45 kg。

对于图7中的简化模型1，立柱上端的梁柱节点和下端的柱脚节点分别简化为一个转动弹簧。当梁柱节点由一根横梁与立柱组成时，其抗弯刚度为Kb1；柱脚抗弯刚度为Kc1。Kb1和Kc1的取值与第3节相同。因为多通道货架的中间立柱与两根横梁相连，其节点抗弯刚度为2Kb1；而边柱只与一根横梁相连，其节点抗弯刚度为Kb1。假定货架一个立柱的平均梁柱节点抗弯刚度为Kbm，对于单通道货架，只有两列边柱，Kbm=Kb1；对于双通道货架，有两列边柱和一列中柱，Kbm=4Kb1/3；对于三通道货架，有两列边柱和两列中柱，Kbm=6Kb1/4。

对于图7中的简化模型2，采用水平梁单元来代替模型1中的转动弹簧，使此模型更加便于模拟计算。上下横向梁单元的长度lb和lc分别为：

lb=3EI/Kbm

(8)

lc=3EI/Kc1

(9)

图7中的两种简化计算模型经过模态分析得到的基本频率fG是相同的(见表3)。由于忽略了一些连接构件对立柱弯曲变形的影响，即减弱了对立柱的约束，简化模型的基本频率比试验结果小一些。

5 结 论

通过对驶入式钢货架的自由振动试验研究和数值分析，得到如下结论：

(1) 货架近似按照结构第一阶振型进行振动。由自由振动位移曲线得到的货架自振频率和阻尼比。其中，自振频率比较稳定，而阻尼比的规律性较差。

(2) 设置顶部水平支撑对货架试件自振频率和阻尼比影响不大，而设置背部竖向支撑可增大货架试件的自振频率，并且减小货架的阻尼比。没有竖向支撑货架的阻尼比平均值为5.94%，而有竖向支撑货架的阻尼比平均值为1.98%。驶入式货架上存储的货物使货架的自振频率变小。货物通道个数的增加只会增大有竖向支撑货架的自振频率。

(3) 通过模态分析和瞬时动力分析，基于梁单元的有限元模型可有效地计算货架的基本自振频率，并且获得货架的振动曲线。

(4) 在没有设置竖向支撑的货架中，各根立柱的振动是同步的，由此提出了两种计算此类货架基本频率的简化计算模型。

[1]CECS23:90, 钢货架结构设计规范 [S]. 北京: 中国工程建设标准化协会, 1990.

[2]MH16.1, Specification for the design, testing and utilization of industrial steel storage racks [S]. Charlotte, USA: Rack Manufacturers Institute (RMI), 2008.

[3]EN 15512, Steel static storage-systems Adjustable pallet racking systems-Principles for structural design [S]. Brussels, Belgium: European Committee for Standardization (CEN), 2009.

[4]王拓, 赵宪忠, 陈以一. 组装式钢货架结构研究现状 [J]. 建筑钢结构进展, 2010, 12(6):1-10.

WANG Tuo, ZHAO Xian-zhong, CHEN Yi-yi. State of the art on assembled steel storage racks [J]. Progress in Steel Building Structures, 2010, 12(6): 1-10.

[5]李晓东, 李永录. 钢货架结构倒塌实例分析 [J]. 钢结构, 2012, 27(7): 49-51.

LI Xiao-dong, LI Yong-lu. Case study for collapse of a steel pallet rack structure [J]. Steel Construction, 2012, 27(7): 49-51.

[6]Gilbert B P, Rasmussen K J R. Impact tests, parametric impact studies and design impact forces on drive-in steel storage racks [R]. Research Report R903, School of Civil Engineering, University of Sydney, 2009.

[7]Zhang H, Gilbert B P, Rasmussen K J R. Drive-in steel storage racks Ⅱ: reliability-based design for forklift truck impact [J]. Journal of Structural Engineering, 2012,138(2): 148-156.

[8]Hua V, Rasmussen K J R. The dynamic study of drive-in racks under horizontal impact load [R]. Research Report R915, School of Civil Engineering, University of Sydney, 2011.

[9]崔迪, 李宏男, 宋钢兵. 形状记忆合金混凝土柱动力特性试验研究 [J]. 振动与冲击, 2010, 29(4):150-154.

CUI Di, LI Hong-nan, SONG Gang-bing. Experimental study of dynamic properties of SMA reinforced concrete columns [J]. Journal of vibration and shock, 2010, 29(4): 150-154.

[10]Gilbert B P, Rasmussen K J R. Finite element modelling of steel drive-in rack structures [R]. Research Report R901, School of Civil Engineering, University of Sydney, 2009.

[11]Chopra A K. 结构动力学理论及其在地震工程中的应用(影印版)[M]. 北京：清华大学出版社，2005.