圆柱碰撞冲击噪声理论分析与数值仿真
李应刚, 陈天宁, 王小鹏, 于坤鹏,张 超
(西安交通大学 机械工程学院 机械结构强度与振动国家重点实验室,西安 710049)
冲击噪声具有极高的瞬态声压峰值和极短的持续时间,世界各国经过试验都制定了相应的冲击噪声的安全标准。但由于瞬态冲击碰撞的复杂性,对于冲击噪声的产生机理和冲击噪声的计算方法一直没有深入详细的研究。为了有效的控制冲击噪声,必须深入了解冲击噪声的发生机理。Akey[1]对冲击噪声研究进行综述,按照产生机理不同将冲击噪声进行分类。Nishimura等[2]研究了两球体碰撞冲击噪声机理,并进行了实验对比验证;Koss等[3]对两球体碰撞冲击进行了理论分析,利用Hertz接触理论推导了两球体碰撞冲击辐射声压的函数关系式;Richards等[4-6]总结了最近20年来有关的冲击噪声研究理论和实验方面的成果,分析了冲击噪声的发声机理,提供了理论研究方法和实验测量手段。然而上述文献大多是针对于弹性球体点接触碰撞冲击辐射噪声问题开展的研究。文献[7-10]对冲击板的瞬态冲击噪声进行了数值仿真和实验研究,提出了瞬态冲击噪声的主动控制方法。
工业生产中许多机械碰撞冲击噪声可归结为圆柱碰撞冲击噪声,如圆柱铰链接触碰撞噪声及齿轮啮合冲击噪声等。对于满足Hertz接触理论假设的两平行轴线的圆柱体接触可以采用平面应变问题的方法处理,但两柱体间的弹性趋近量没有准确解。文献[11-12]对接触碰撞模型进行了综述及对比分析。文献[13-15]根据Hertz接触理论推导了圆柱接触理论模型,然而以上三种理论模型均为非线性隐式方程,求解过程需要采取数值积分方法,不利于碰撞冲击噪声理论预估。Palmgren基于Hertz接触理论提出了一种显式的线弹性接触数学模型,具有较高计算精度。而对于圆柱碰撞冲击噪声问题,Yufang等[16]研究了两圆柱撞击发声机理,基于Hertz点接触理论模型及圆柱体声波方程推导了两圆柱体碰撞冲击的接触力及辐射声压随时间变化的函数关系式。然而文献中将圆柱体线接触模型简化为点接触模型,将线接触的矩形接触面简化为点接触的椭圆形接触面,使圆柱碰撞接触力和冲击噪声理论预估产生较大偏差。
本文基于接触动力学相关理论和Palmgren圆柱体线接触理论模型,建立了圆柱碰撞冲击理论数学模型,推导了圆柱碰撞冲击接触力随时间变化的函数关系式;利用声学理论对圆柱碰撞冲击辐射噪声进行了理论预估。采用有限元法(FEM)与瞬态边界元法(TBEM)相结合的瞬态噪声数值计算方法,对圆柱碰撞冲击噪声进行数值仿真;将有限元法(FEM)计算结果作为状态变量导入瞬态边界元法(TBEM)分析圆柱碰撞瞬态辐射声场,实现了瞬态冲击噪声辐射声波的可视化。理论预估结果与数值仿真结果吻合较好。
1 理论建模
1.1 圆柱碰撞冲击理论
基于接触动力学理论和Palmgren圆柱体线弹性接触模型,两圆柱接触冲击时接触力与变形关系:
F=Kδn
(1)
式中:F为接触力(N);δ为接触变形(m);n为圆柱接触非线性指数,本文采用Palmgren圆柱体线弹性接触模型n=10/9。K取决于碰撞物体材料和结构形状
(2)
式中:E1、E2为材料的弹性模量(Pa);υ1、υ2为材料的泊松比;L为圆柱体长度(m)。
根据牛顿运动定律,圆柱体接触碰撞的运动微分方程为:
(3)
式中:m1、m2为圆柱体质量(kg);v1、v2为圆柱体瞬时速度(m/s)。将式(1)带入式(3)中,则有:
(4)
式中:mred为圆柱体等效质量。
(5)
对δ作积分可得:
(6)
式中:v0=(v2-v1)t=0为圆柱碰撞初始时刻冲击速度,在最大压缩δm时,dδ/dt=0。由式(1)与式(6)可得圆柱碰撞最大冲击力Fm表达式为
(7)
假设圆柱体接触碰撞过程中冲击力、冲击加速度与时间近似为一个半波正弦脉冲。半波正弦脉冲角频率为ωc=π/tc。则圆柱碰撞冲击力表达式为:
F(t)=Fmsin(ωct)
(0≤t≤tc)
(8)
由冲击加速度可得圆柱碰撞冲击速度表达式为:
(9)
1.2 圆柱碰撞冲击辐射噪声
根据声学理论,柱面波动方程为
(10)
式中:Φ为速度势函数;c为空气中声速;ρ为空气密度;p为声压;ur为径向振动速度。
圆柱体以V0ejωt振动时速度势函数为:
(11)
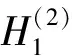
(12)
(13)
代入式(11)中可得
(14)
声波从圆柱接触碰撞处传播至P点波动时间为
t*=(r-R)/c
(15)
用V(t)代替(14)式中V0cosθ可得速度势函数为
(16)
由式(10)可得圆柱体在P点处辐射声压表达式为
(17)
则两圆柱体碰撞冲击在P点声压表达式为:
pred(r,θ,t)=p1(r1,θ1,t)+p2(r2,θ2,t)
(18)
2 数值仿真
为了验证圆柱碰撞接触力和冲击噪声理论预估的正确性,提出有限元法(FEM)与瞬态边界元法(TBEM)相结合的瞬态噪声数值计算方法,将有限元法(FEM)计算结果作为状态变量导入瞬态边界元法(TBEM)分析圆柱碰撞瞬态辐射声场,实现了瞬态冲击噪声辐射声波的可视化。
2.1 圆柱碰撞冲击有限元仿真
本文使用ANSYS/LS-DYNA软件研究圆柱碰撞冲击有限元仿真分析[17]。ANSYS/LS-DYNA将显式有限元程序LS-DYNA和ANSYS程序结合起来。用LS-DYNA的显式算法能快速求解接触碰撞问题。
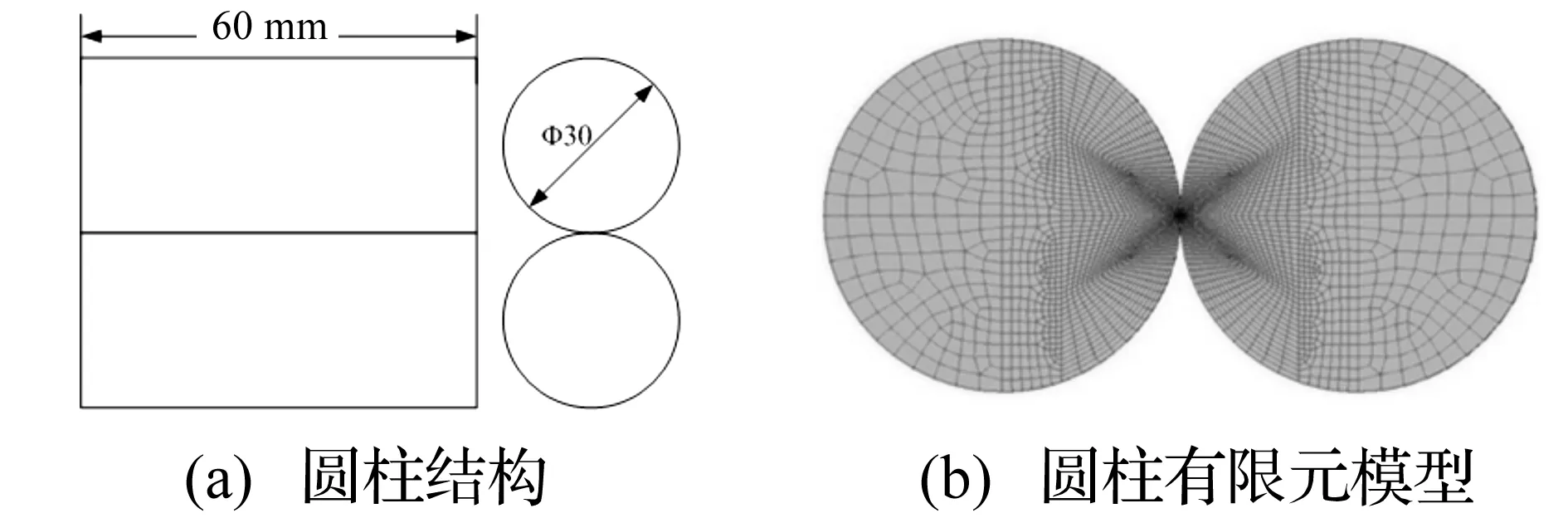
图1 圆柱碰撞冲击模型
圆柱碰撞冲击有限元模型如图1所示。两圆柱体半径为15 mm,长度为60 mm。两圆柱体都定义为合金钢材料,密度为7 800 kg/m3,弹性模量为2.06×1011Pa,泊松比为0.3。碰撞冲击噪声取决于两圆柱碰撞冲击相对速度。考虑到圆柱接触冲击对称性,两个圆柱体分别施加0.5 m/s的相对水平初始速度。
有限元数值仿真计算获得了圆柱碰撞冲击接触力,接触力时间历程曲线近似为半波正弦脉冲,与理论分析假设吻合。对比数值仿真结果、理论分析结果以及赫兹点接触模型计算结果如图2所示,其中实线为数值仿真结果,虚线为公式(8)接触力理论预估结果,点划线为Hertz点接触模型计算结果[16]。由图可知理论预估结果与数值仿真结果吻合较好,而Hertz点接触模型计算结果会产生较大误差。分析原因为Hertz接触模型将圆柱体线接触简化为点接触问题,从而使接触碰撞时间延长,接触碰撞力幅值降低。
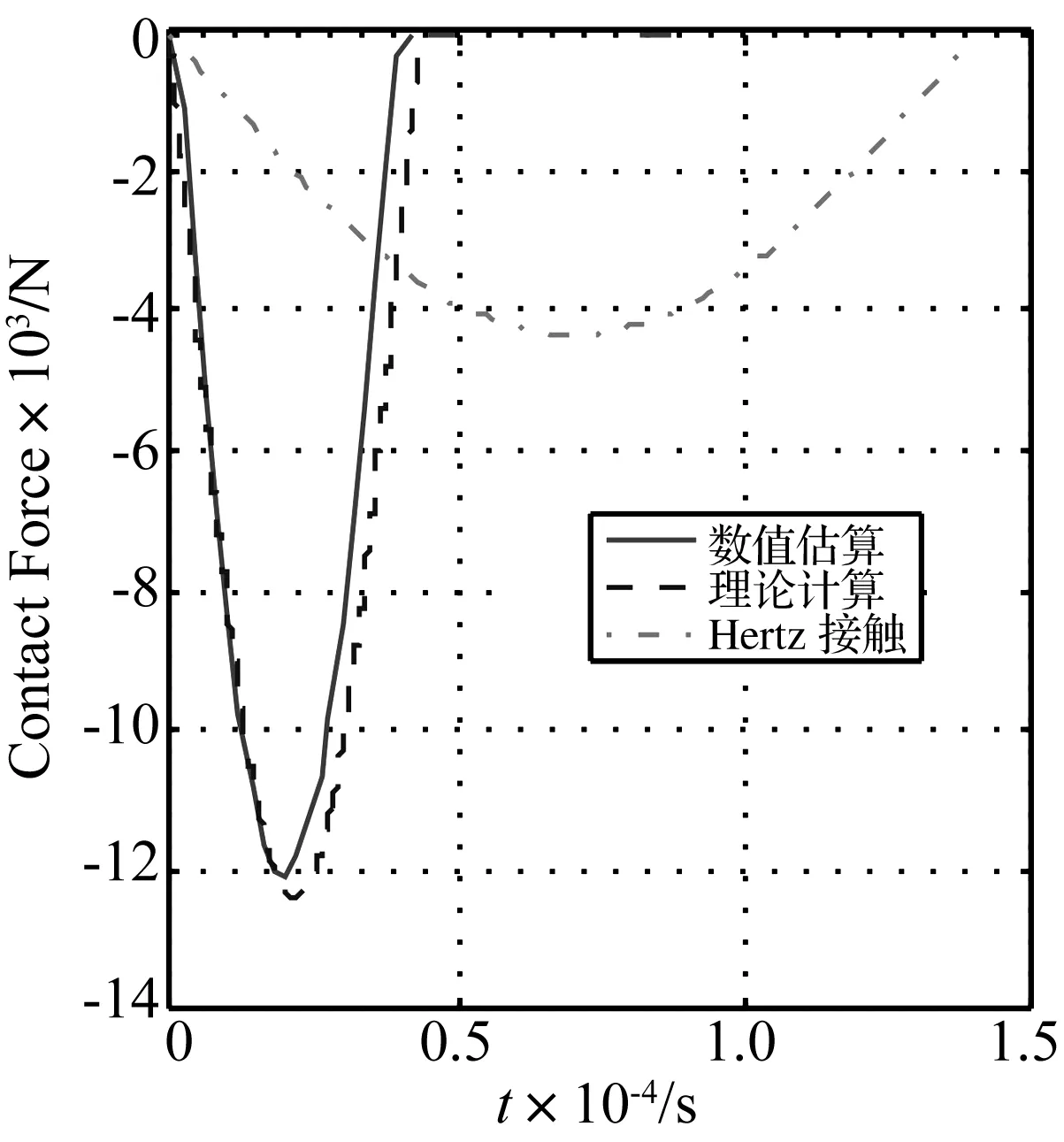
图2 接触力时间历程曲线
按照发声的机理来划分,冲击噪声主要分为自鸣噪声和加速度噪声。为了分析研究圆柱碰撞冲击噪声发生机理及组成成分,提取了圆柱有限元模型中节点加速度曲线如图3所示。对节点加速度时间响应曲线进行傅里叶变换得到加速度频谱图如图4所示。考虑圆柱碰撞冲击过程中将会激起圆柱模态振动,对圆柱进行模态分析得到圆柱前10阶固有频率如表1所示。

表1 圆柱固有频率
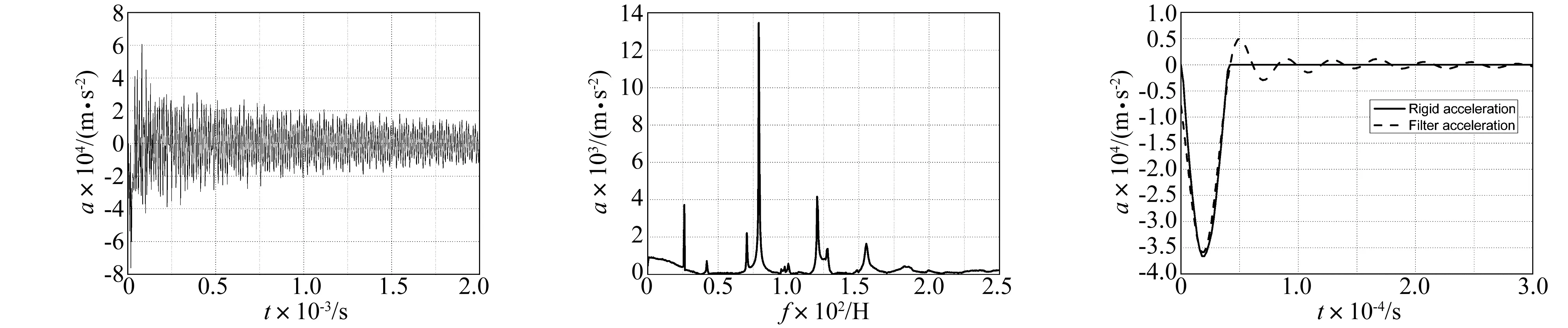
图3 加速度时间历程曲线
对比分析加速度频谱图及圆柱模态分析结果可知,圆柱加速度频谱中峰值频率对应于圆柱的模态频率。考虑人耳能够感知的频率范围为20 kHz以下,从加速度频谱图中发现共振峰频率都高于20 kHz,说明圆柱碰撞冲击过程中自鸣噪声频率都高于人耳感知频率范围,此时人耳感知碰撞冲击噪声主要是加速度噪声。
将圆柱碰撞冲击过程中节点加速度时间响应曲线采取低通滤波处理,根据圆柱碰撞冲击接触力曲线可得圆柱碰撞冲击刚体加速度曲线。节点加速度低通滤波处理后曲线及刚体加速度曲线如图5所示。对比分析刚体加速度及滤波加速度曲线可知圆柱碰撞冲击噪声主要是由于刚体加速度辐射噪声产生。
2.2 辐射噪声瞬态边界元仿真
本文采用LMS Virtual Lab软件边界元法进行圆柱碰撞冲击瞬态辐射噪声研究。边界元法基本思想是将微分方程转化为边界上定义的边界积分方程,并将边界离散化,使积分方程成为只含有边界积分节点未知量的代数方程组,通过求解获得边界节点参数,进一步求得分析域内部参数。
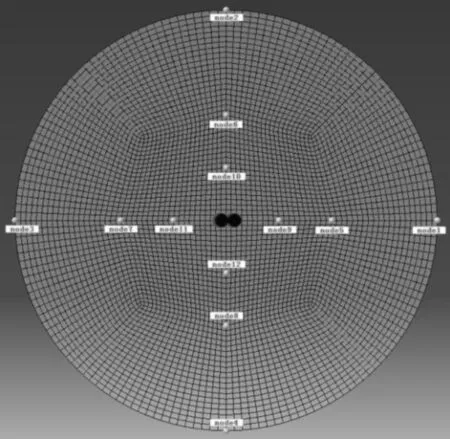
图6 瞬态声学边界元模型
圆柱碰撞冲击瞬态声学边界元模型如图6所示。边界元网格及场点网格都是在ANSYS软件中生成为CDB格式文件导入Virtual Lab Acoustics。边界元网格为圆柱碰撞冲击有限元模型的表面网格,采用三角形单元划分网格。场点网格为半径500 mm圆形区域。
将ANSYS/LS-DYNA软件计算得到的圆柱碰撞冲击振动位移导入Virtual Lab Acoustics进行瞬态边界元分析,实现瞬态冲击噪声辐射声波的可视化。圆柱碰撞冲击瞬态辐射声波传播过程如图7所示。由图可知,圆柱碰撞冲击噪声存在明显的波动过程,在碰撞冲击方向声压幅值较大,垂直于碰撞冲击方向声压较小。随着辐射声波传播,冲击噪声辐射能量发生扩散,辐射声压幅值逐渐降低。

图7 瞬态辐射声波传播
为了验证圆柱碰撞冲击噪声理论模型,提取声场中节点1的辐射声压时间历程曲线并进行对比如图8所示。图中实线为数值仿真结果,虚线为公式(18)理论预估结果,点划线为Hertz点接触模型计算结果。对比数值仿真结果、理论预估结果可知理论分析结果与数值仿真结果吻合较好。而Hertz点接触模型计算结果声压幅值较小,持续时间较长。分析原因为Hertz点接触模型将圆柱体线接触简化为点接触问题,使接触碰撞时间延长,接触碰撞力幅值降低,从而导致加速度幅值降低,而圆柱碰撞冲击噪声主要由加速度辐射产生,因而预估声压幅值较小。
为了研究圆柱碰撞瞬态声辐射特性,提取场点网格上同一声辐射方向不同距离节点node1和node5的声压时间历程曲线如图9所示。分析可知,同一辐射方向上,场点声压随着距离增大而降低。提取场点网格上不同声辐射方向距离相同的两个节点node1和node2的声压时间历程曲线如图10所示。分析可知不同辐射方向上距离碰撞冲击声源等距的场点声压不同,即圆柱碰撞辐射声场具有方向性。根据圆柱碰撞冲击辐射声场辐射特性可知,圆柱碰撞辐射声场可以理解为平面偶极源的辐射声场,在距离声源较远处辐射声压与距离成反比,且辐射声场具有明显的方向性。
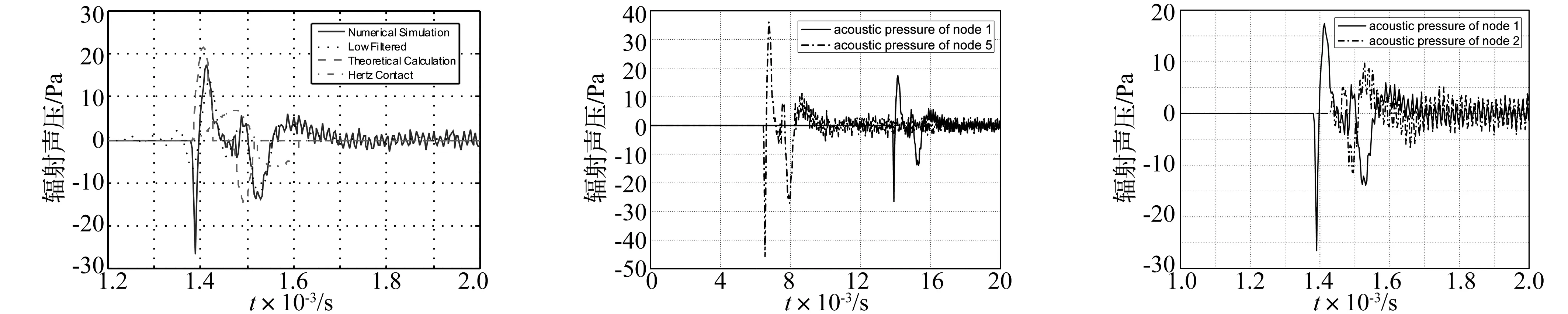
图8 辐射声压时间历程曲线

图11 接触力时间历程曲线
3 圆柱碰撞冲击参数分析
3.1 圆柱碰撞冲击速度影响
为了研究冲击速度对圆柱碰撞冲击的影响,对比分析五种冲击速度条件下圆柱碰撞冲击力及辐射声压变化情况。不同冲击速度条件下圆柱碰撞冲击接触力时间曲线如图11所示,接触力与冲击速度关系曲线如图12所示,辐射声压与冲击速度关系如图13所示。由图可知在弹性接触碰撞范围内,圆柱碰撞冲击接触力以及辐射声压与冲击速度成正比,接触冲击时间不随冲击速度变化而变化。
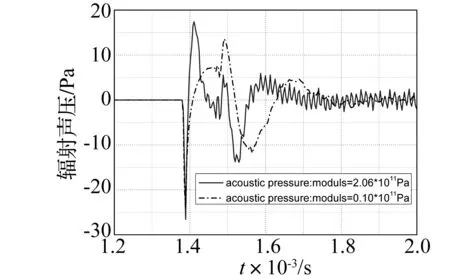
图14 辐射声压时间历程曲线
3.2 圆柱材料弹性模量影响
为了研究材料弹性模量对圆柱碰撞冲击的影响,对比分析了不同材料弹性模量条件下圆柱碰撞冲击噪声变化情况。图14为两种材料弹性模量条件下辐射声压时间历程曲线。由图发现,虽然圆柱碰撞辐射加速度噪声与材料弹性模量呈指数关系,然而总辐射声压与弹性模量并不是呈指数关系变化。分析原因为材料弹性模量变化改变了圆柱固有频率,材料弹性模量减小,固有频率降低,导致圆柱碰撞的自鸣噪声增大,频率成分降低。人耳感知碰撞噪声频率成分不再仅仅是加速度噪声,而是加速度噪声和自鸣噪声叠加。
4 结 论
(1) 基于接触动力学相关理论及弹性体线接触理论模型,推导了圆柱碰撞冲击理论模型,结合声学理论对圆柱碰撞冲击噪声进行了理论预估。
(2) 采用有限元法(FEM)与瞬态边界元法(TBEM)相结合的瞬态噪声数值仿真方法,对圆柱碰撞冲击噪声进行数值仿真,实现了瞬态辐射声波的可视化。分析圆柱碰撞冲击噪声机理可知圆柱碰撞冲击噪声主要由加速度辐射噪声产生。圆柱碰撞冲击噪声存在明显的波动过程,在碰撞冲击方向声压幅值较大,垂直于碰撞冲击方向声压较小,辐射声场具有明显指向性。随着辐射声波传播,冲击噪声辐射能量发生扩散,辐射声压幅值逐渐降低。
(3) 对比理论分析结果、数值仿真结果以及Hertz点接触模型计算结果可知,理论分析结果与数值仿真结果吻合较好,而Hertz点接触模型将圆柱体线接触模型简化为点接触模型,导致接触时间延长,接触力和冲击噪声幅值降低。表明基于圆柱体线弹性接触模型相较Hertz点接触理论模型能够更准确实现接触力和冲击噪声理论预估。
(4) 研究了冲击速度和材料弹性模量对圆柱碰撞冲击的影响。结果表明在弹性碰撞条件下,圆柱碰撞冲击接触力以及辐射声压与冲击速度成正比,接触冲击时间不随冲击速度变化而变化。材料弹性模量减小,圆柱体固有频率降低,导致圆柱碰撞的自鸣噪声增大,频率成分降低。此时圆柱碰撞冲击噪声不再仅仅是加速度辐射噪声产生,而是加速度噪声和自鸣噪声叠加。
[1]Akey A. A review of impact noise[J]. Journal of the Acoustical Society of America,1978,64(4):977-987.
[2]Nishimura G, Takahashi K. Impact sound by mutual collision of two steel balls[J]. Bulletin of the Japan Society of Precision Engineers,1963,(1):47-51.
[3]Koss L, Alfredson R. Transient sound radiated by spheres undergoing an elastic collision[J]. Jaurnal of Sound and Vibration, 1973,27(1):59-68.
[4]Richards E, Westcott M, Jeyapalan R. On the prediction of impact noise, I: Acceleration noise[J]. Jaurnal of Sound and Vibration, 1979,62(4):547-575.
[5]Richards E, Westcott M, Jeyapalan R. On the prediction of impact noise, II: Ringing noise[J]. Jaurnal of Sound and Vibration, 1979,65(3):419-451.
[6]Richards E. On the prediction of impact noise, III: Energy accountancy in industrial machines[J]. Jaurnal of Sound and Vibration, 1981,76(2):187-232.
[7]Van Niekerk J, Tongue B, Packard A. Active control of a circular plate to reduce transient noise transmission[C]. Publisher, City, 1995.
[8]Pinte G, Desmet W, Sas P. Active control of repetitive transient noise[C]. Publisher, City, 2007.
[9]Ross A, Ostiguy G. Propagation of the initial transient noise from an impacted plate[C]. Publisher, City, 2007.
[10]Blais J F, Ross A. Forward projection of transient sound pressure fields radiated by impacted plates using numerical Laplace transform[C]. Publisher, City, 2009.
[11]Pereira C M, Ramalho A L, Ambrósio J A. A critical overview of internal and external cylinder contact force models[C]. Publisher, City, 2011.
[12]Machado M, Moreira P, Flores P, et al. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory[C]. Publisher, City, 2012.
[13]Goldsmith W, Impact: the theory and physical behaviour of colliding solids[C]. Dover Pubns, 2001.
[14]Johnson K L. Contact mechanics, Cambridge Univ Pr, 1987.
[15]Radzimovsky E I. Stress distribution and strength condition of two rolling cylinders pressed together[C]. Publisher, City, 1953.
[16]Yufang W, Zhongfang T. Sound radiated from the impact of two cylinders[J]. Jaurnal of Sound and Vibration, 1992, 159(2):295-303.
[17]白金泽. LS-DYNA3D 理论基础与实例分析[M]. 科学出版社, 2005.

