高层隔震结构实空间解耦及地震作用取值分析

李创第, 陈欧阳, 葛新广 , 李 暾, 邹万杰, 薛建朝

(1. 广西科技大学 土建学院，广西 柳州 545006；2. 广西大学 土建学院，南宁 530004)

地震作用取值是抗震设计的基础，我国抗震规范采用反应谱法计算地震作用。近年来，隔震技术已应用于高层结构[1～3]。由于高层隔震结构具有非经典高阻尼，且需要考虑多振型影响，其工程分析体系具有非对称质量和非经典阻尼性质[1]，无法通过经典实模态法解耦。尽管多高层隔震结构响应分析有精确的复数域和近似的实数域两类分析法，现有的多高层隔震结构地震作用分析法主要基于三种近似实数域响应分解法，即：① 强行振型解耦法[3-5]；② 等效阻尼比解耦法[2]；③ 拉氏变换与实振型分解组合法[6-8]。

基于强行解耦的分析法是目前广泛采用的方法[3-5]，其实质是完全忽略非经典阻尼矩阵的耦联，对结构强行解耦后，按经典结构近似组合计算；基于等效阻尼比解耦的分析法是忽略振型间的交叉阻尼，运用Hamilton原理，获得振型近似等效阻尼比，实现结构解耦后，按经典结构计算[2]；基于拉氏变换与实振型组合的地震作用取值分析，其实质是先将隔震结构两位移响应分量近似分解为系列标准振子的位移与拟速度的线性组合，然后基于3个假设计算地震作用[6, 7]，即：① SRSS组合，不考虑各种相关性；② 位移谱、速度谱、拟速度谱在小阻尼成立的相互关系适用于高阻尼；③ 速度谱在长周期段基本为常数的性质适用于短周期段。事实上，上述3个假设均不严格成立，特别是假设②，在高阻尼时误差相当大[9]，同时拟速度响应也不是物理意义明确的真实响应，将使结构组合分析复杂化。

最近的研究表明：用于判断各种实数域近似法精度与适用范围的各种定量指标[10-11]并不具有一般性，非经典阻尼矩阵耦联指标小并不一定能保证近似解耦的误差小[12-13]；同时，为提高结构近似组合计算精度，基于白噪声激励的结构近似相关组合系数应修正为基于与反应谱对应的功率谱的改进近似相关组合系数[14]。因此，上述现有的多高层隔震结构地震作用分析法均建立在近似响应与近似组合分析之上，且近似响应分析并不一定能保证计算精度，需建立高层隔震结构基于精确响应与精确组合分析之上的地震作用分析法。

本文首先建立非对称非经典结构响应的实空间精确解耦法，将高层隔震结构位移响应方差在实空间上精确分解为系列标准振子的位移与速度响应方差的线性组合，然后利用系列标准振子最大响应与反应谱的对应关系，建立高层隔震结构基于精确响应与精确组合分析之上基于反应谱的地震作用取值解析解法。

1 高层隔震结构响应实空间精确解耦

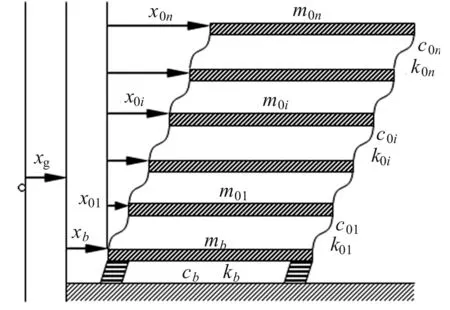
图1 结构计算简图

(1a)

(1b)

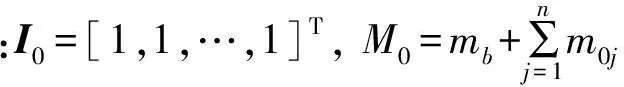
将位移向量x0按高层结构多振型展开，即：

(N≤n)

(2)

并设Mi、ξ0i、ω0i、ri，(i=1～N)，分别为振型Φi对应的广义质量、阻尼比、圆频率和振型参与系数，则方程(1)可化为：

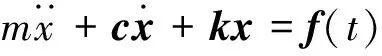
(3)

式中：

(4a)

c=diag[2ξ01ω01… 2ξ0Nω0N2ξbωb]

(4a)

(4b)

x=[x1…xm]T=[x1…xNxb]T

(4c)

r=[r1…rm]T=[r1…rN1]T

(4d)

(4e)

(4f)

式(3)是非对称质量与非经典阻尼方程，实模态法无法解耦，但可用实空间法解耦。

方程(3)的2m=2N+2个复特征根λj及其对应的右、左复特征向量uj、vj可由下列方程确定[15]：

det[D(λ)]=det[mλ2+cλ+k]=0

(5a)

D(λj)uj=0;D(λj)Tvj=0

(j=1～2m)

(5b)

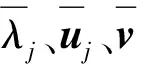
u=[u1u2…um]

(6a)

v=[v1v2…vm]

(6b)

λ=diag[λj]，(j=1～m)

(6c)

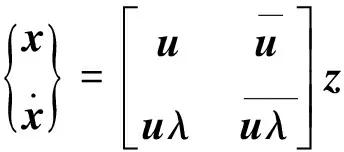
(6d)

则根据复模态法理论[15]，方程(3)可解耦为：

(7)

式中：

(8)

令：

(9)

则有：

(10)

式中：I为m阶单位阵，p1(t)、p2(t)均为m维待求向量。将式(10)代入式(7)，前乘w，并利用：

(11)

经化简，可得：

(12a)

(12b)

式中：

(j=1～m)

(13a)

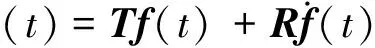
(13b)

(13c)

(13d)

Re表示取复数的实部。

对方程(12)取拉氏变换，可得：

(14a)

(14b)

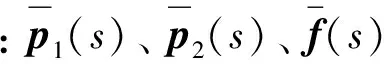
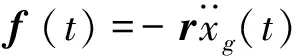
α=Tr=[α1…αm]T

(15a)

β=Rr=[β1…βm]T

(15b)

δ(t)=[δ1(t) …δm(t)]T

(16a)

(j=1～m)

(16b)

则由式(14) ～ (16)及拉氏变换，可得：

(17a)

(17b)

故由式(6d)、式(10)、式(17)，得结构响应为：

(18a)

(18b)

式中：

(19a)

B2=[B2kj]=A0diag[βj]+B0diag[αj-2ξjωjβj]

(19b)

(19c)

G2=D0diag[βj]+G0diag[αj-2ξjωjβj]

(19d)

(20a)

(20b)

(20c)

(20d)

由于矩阵A2、B2、D2、G2均为实矩阵，显然式(18)和式(16)构成了非对称非经典结构响应的实空间精确解耦，将结构位移与速度响应在实空间上精确表示为物理上可实现的真实系列标准振子的位移与速度响应的线性组合。

2 高层隔震结构响应方差标准振子精确分解

由式(18b)，广义位移响应x(t)的各分量为：

(k=1～N+1)

(21)

故由式(2)，高层结构与隔震层的各层层间相对位移si(t)为：

si(t)=x0,i-x0,i-1=

(i=1～n)

(22a)

sn+1(t)=xb(t)=xN+1(t)=

(22b)

式中：Φi,k和Φi-1,k分别为振型Φk的第i及第(i-1)个分量；

(23a)

(23b)

φn+1,j=A2(N+1)j;ψn+1,j=B2(N+1)j

(23c)

故由式(22)和标准振子方程(16b)以及随机振动频域法，得隔震结构各层间位移分量的平稳响应方差为：

(i=1～n+1)

(24)

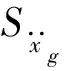
aijk=φijφikbijk=ψijψik

(25a)

cijk=φijψikdijk=ψijφik

(25b)

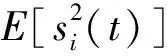
(26a)

(26b)

(26c)

经简化得：

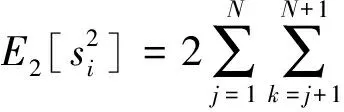
(27)

式中：

N(ω)=N0+N2ω2+N4ω4+N6ω6

(28)

(29)

显然，式(29)中aijk、bijk、(dijk-cijk)，(j≠k)分别表示标准振子的位移、速度和位移与速度各自之间的互相关影响。

由于N(ω)是ω的6次多项式，故可进行恒等变换：

(30)

式中：Jijk、Lijk、Qijk、Wijk为待求常数。由于：

(31a)

(31b)

将式(31)代入式(30)，并比较方程(30)两边关于ω0、ω2、ω4、ω6的系数，得：

(32)

式中：

(33)

求解四元一次方程组(32)，即求得常数Jijk、Lijk、Qijk、Wijk，其具体表达式已列入文献[16]。

故由式(26)、(27)、(30)，得隔震结构各层间位移分量响应方差精确分解为系列标准振子位移与速度响应方差线性组合的解析式为：

(i=1～n+1)

(34)

式中：I1j、I2j分别是标准振子(16b)的位移与速度响应方差，即：

(j=1～N+1)

(35a)

(j=1～N+1)

(35b)

由于相关组合系数Jijk、Lijk、Qijk、Wijk是通过恒等变换解析获得，是结构相关组合系数取值的解析解，不产生任何误差，均比现有基于方程(16b)与白噪声激励假设或反应谱对应的功率谱激励假设[14]所获得的近似相关组合系数更精确合理。

3 基于反应谱的结构设计响应

3.1 结构设计响应计算式

由于设计响应值simax(t)(i=1～n+1)是响应的最大值，故它可取为峰值因子Cf与响应si(t)的标准差的乘积，即：

(36)

式中：R1j和R2j分别是标准振子δj(t)的最大地震位移与速度响应的平方，即：

(37a)

(37b)

其中：j=1～N+1。故结构设计响应simax(t)的计算，归结于R1j和R2j的(j=1～N+1)计算。

3.2 系列标准振子的R1j(ωj, ξj)和R2j(ωj, ξj)计算

R1j(ωj,ξj)和R2j(ωj,ξj)是下列二阶标准振子的位移谱Sd(ωj,ξj)和速度谱Sv(ωj,ξj)的平方，即：

(38)

(39a)

(39b)

其中：j=1～N+1。由于文献[17]已经建立了由抗震规范加速度谱计算位移谱和速度谱的方法，故R1j(ωj,ξj)和R2j(ωj,ξj)可由规范直接计算，即：

(40a)

(40b)

式中：α(ωj,ξ=5%)为规范加速度谱中周期Tj=2π/ωj、阻尼比ξ=5%所对应的地震响应系数；Bd和Bv分别是位移谱和速度谱的阻尼影响因子，即：

(41)

文献[18]已给出各种ωj、ξj所对应的Bd和Bv取值。

总之，求出R1j(ωj,ξj)和R2j(ωj,ξj)，(j=1～N+1)之后，由式(36)即得结构基于规范反应谱的最大地震极值响应simax(t) ，(i=1～n+1)。

4 高层隔震结构地震作用取值

4.1 地震作用新定义

对于常规结构，我国抗震规范将地震作用定义为结构在地震响应过程中产生的最大惯性力，其依据是在小阻尼假设情况下，加速度谱与位移谱存在对应比例关系，将此地震作用作为等效静态荷载作用于结构所产生的等效静态位移和剪力等于结构在地震响应过程中所产生的位移和剪力响应的最大值[19]。由于隔震结构具有长周期和高阻尼性能，不满足规范关于地震作用定义的小阻尼适用条件，即不能保证上述静态地震作用产生的静态效应等于实际地震动态效应的最大值，因此有必要重新定义隔震结构的地震作用。

由于结构抗震设计的安全取决于地震激励在结构内产生的最大地震位移响应和内力响应(剪力、弯矩、轴力等)小于相应设计允许限值，而相应的抗震设计允许限值是基于材料的标准静力试验而得[20]，因此，等效静态地震作用包含速度相关的阻尼力是不合适的，又因为最大地震内力效应与结构最大地震位移响应存在静力学对应关系，故结构实际地震响应产生的最大动态效应和结构抗震设计的安全完全取决于结构的最大地震位移响应。相对于结构的加速度或绝对加速度响应而言，结构的位移响应更具有本质特性，因为每一时刻的结构内力响应与同时刻的位移响应是线性相关的，每一时刻的内力响应均可从同一时刻的位移响应按结构的静力分析而获得，而加速度或绝对加速度响应则不存在上述对应关系。因此，按静态效应与最大动态效应的等效原则，等效静态地震作用的本质定义是地震激励所产生的结构最大位移响应所对应的等效静态荷载与等效静态内力。

4.2 高层隔震结构基于最大位移响应的地震作用取值

由于已求得高层隔震结构隔震层最大相对地面位移响应xbmax=s(n+1)max，以及隔震层上部高层结构各层最大层间位移响应simax(i=1～n)，故高层隔震结构隔震层等效静态地震剪力作用VEb和上部高层结构各层层间等效静态地震剪力VEi作用分别为：

VEb=kbxbmax=kbs(n+1)max

(42a)

VEi=k0isimax(i=1～n)

(42b)

求出VEb和VEi之后，即可对高层隔震结构进行等效静态抗震设计。

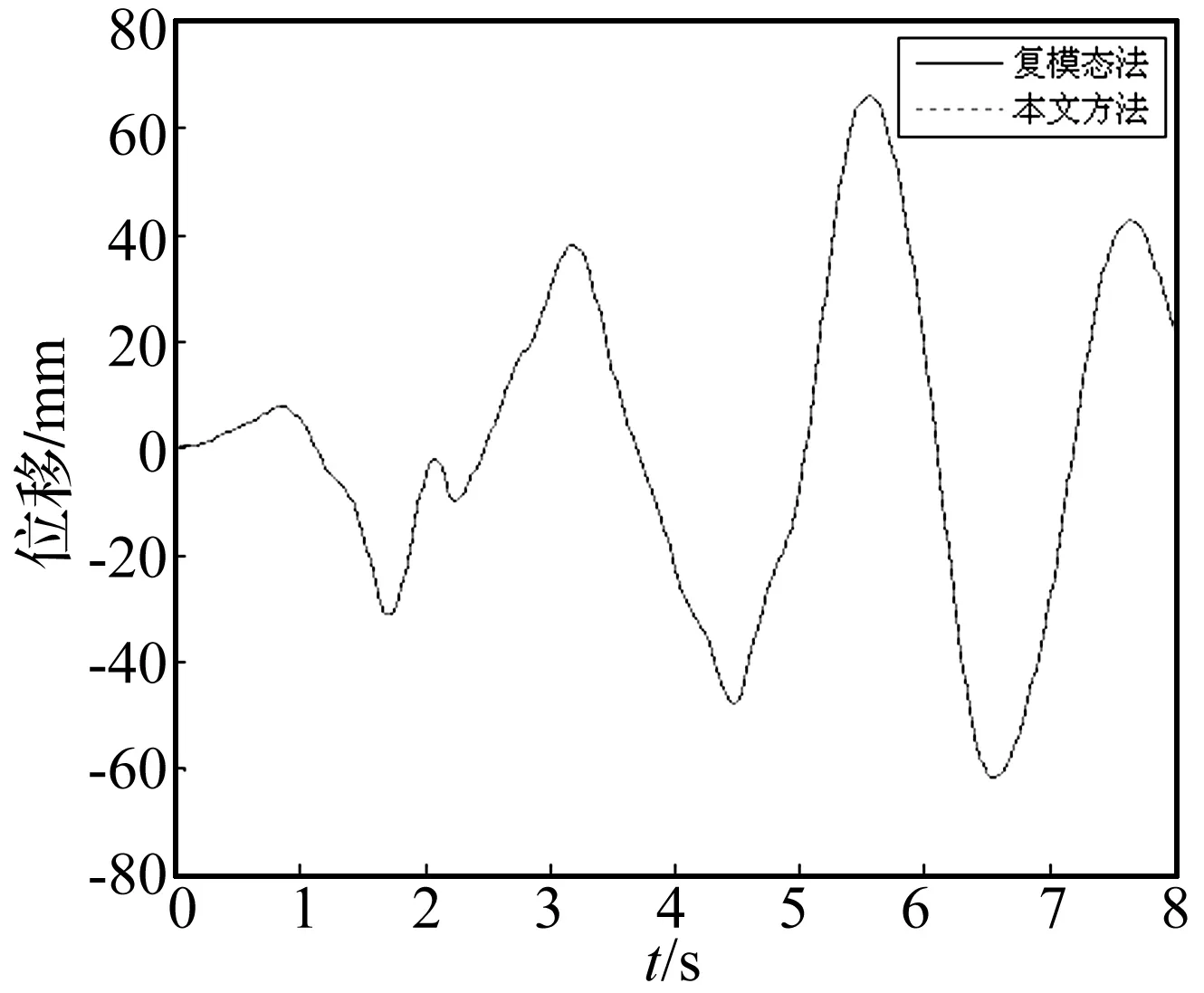
图2 隔震层位移响应(ξb=0.15)

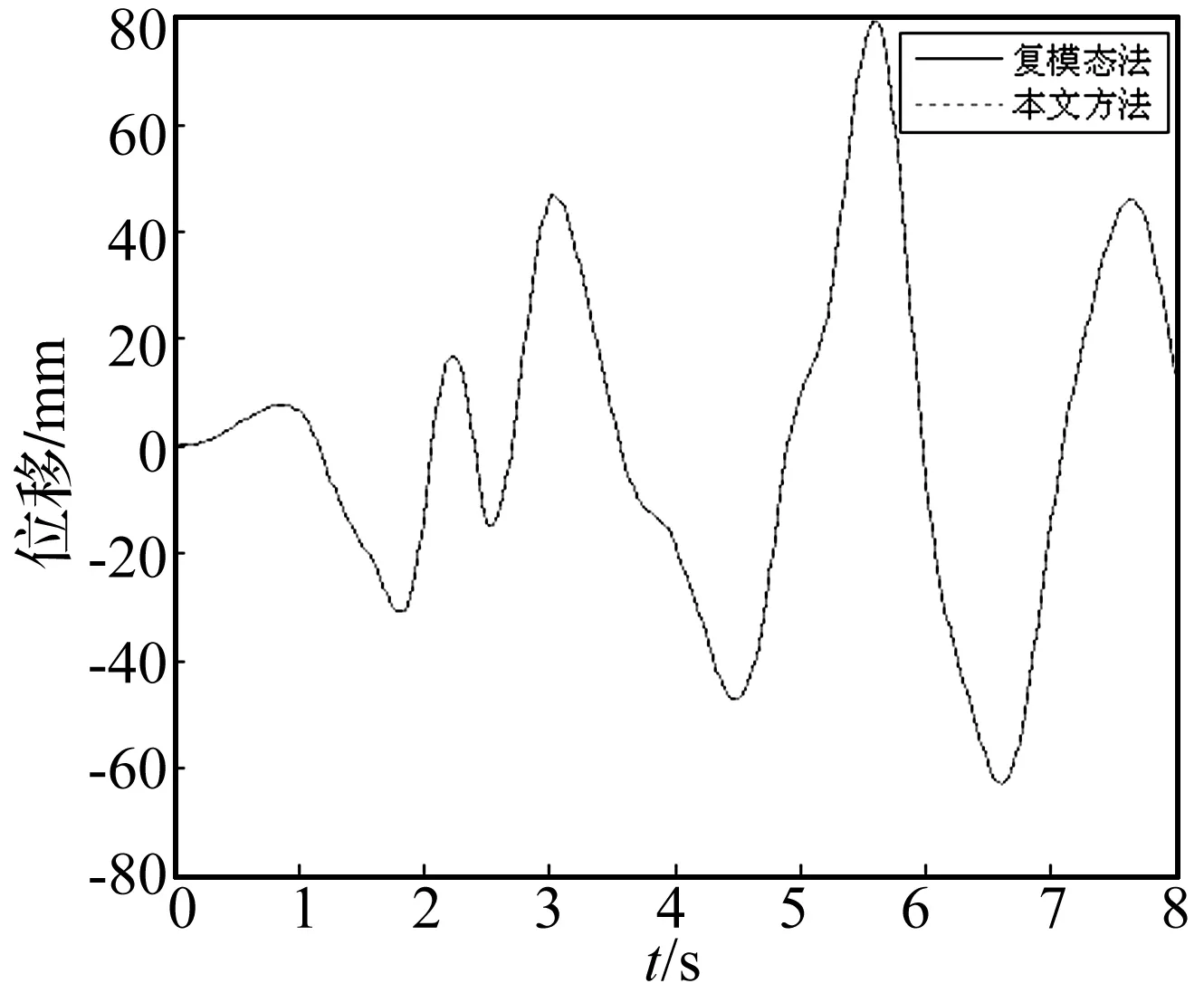
图3 顶层位移响应(ξb=0.15)

5 算 例

某20层钢筋混凝土框架结构房屋，建在地震烈度I=8°，Ⅱ类场地土上，设计分组第二组，Tg=0.4 s。隔震层及其上部框架结构的层间质量和刚度见表1，结构第一至第三自振频率和阻尼比分别为：ω01=4.364 6(1/s)、ξ01=0.05；ω02=11.881 3(1/s)、ξ02=0.05；ω03=18.989 2(1/s)、ξ03=0.05。

(1) 采用200gal EI-centro(1940，S400E)作为输入地震波，隔震层阻尼比ξb=0.05、0.10、0.15、0.20；分别用实空间解耦法和复模态法进行时程响应分析，两种方法计算结果完全相同。限于篇幅，仅列出隔震层相对地面位移和上部结构顶层相对隔震层位移在ξb=0.15时的时程响应结果，如图2和图3所示。

(2) 取谱密度为S0=0.013 87 (m2/s3)的白噪声作为平稳随机地震动激励，分别用实空间解耦法和复模态法进行隔震结构各层层间位移响应方差分析，计算结果如表1所示(其中方差(Ⅰ)是用实空间解耦法所得结果，方差(Ⅱ)是用复模态法所得结果)。从中可以看出两种方法计算结果完全相同。

(3) 基于现行抗震规范反应谱的多遇地震作用下，隔震层相对地面位移和上部框架结构各层相对位移最大值以及隔震层结构各层相应层间地震剪力作用取值如表1所示。

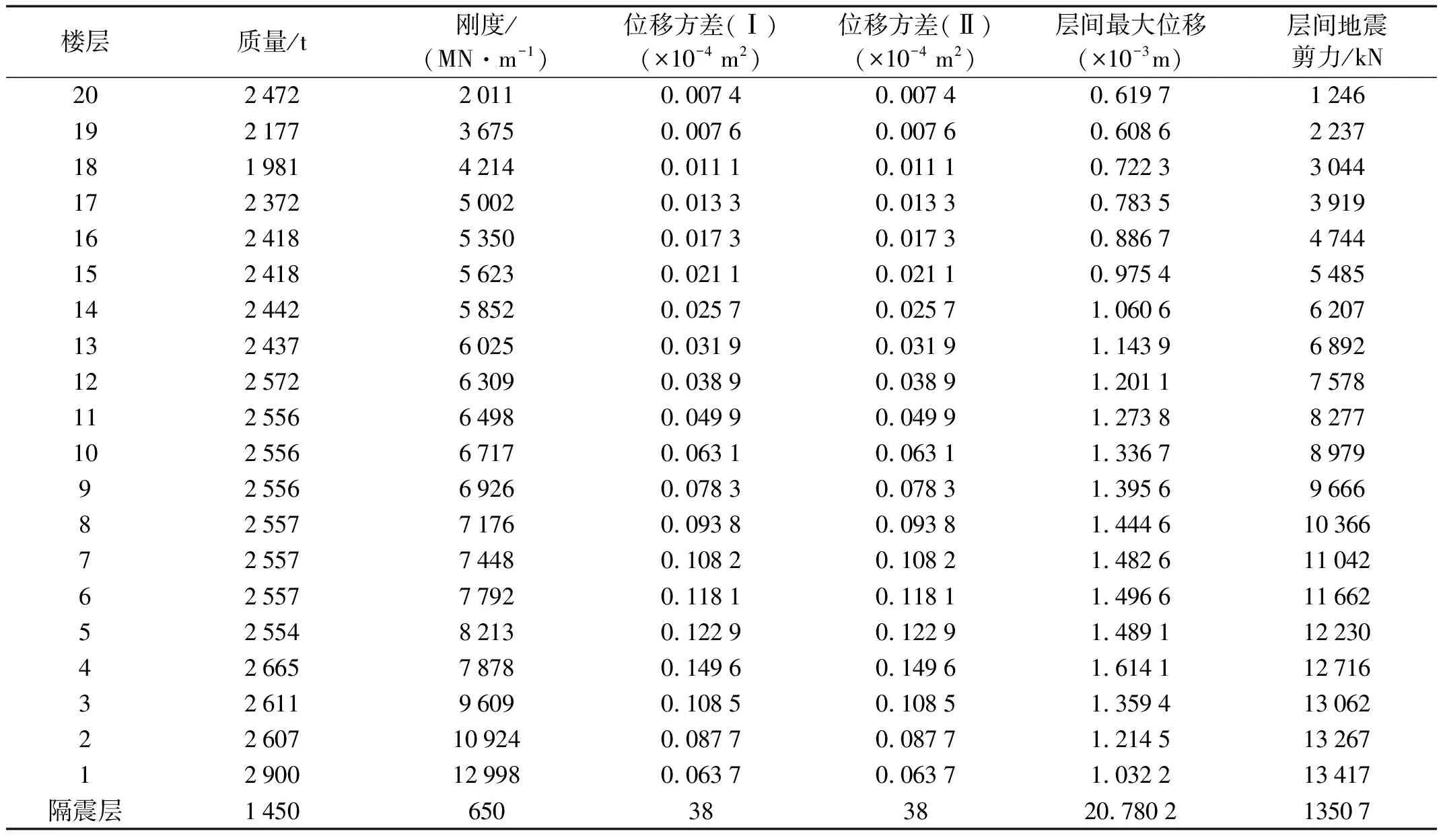
表1 结构参数和层间位移响应方差与层间地震作用剪力取值(ξb=0.20)

时程响应与随机响应分析均表明，实空间解耦法和精确的复模态分析法的计算结果完全相同，验证了所提出方法的正确性。

6 结 论

本文对高层非经典阻尼隔震结构响应的实空间精确解耦及其地震作用取值进行了系统研究，获得了摘要所述结果。虽然所建立的方法是针对多自由度非对称质量与非经典阻尼结构，但所有公式的推导并未对非对称刚度与非对称阻尼矩阵加以限制，故所建立的方法具有一般性，适用于一般非对称质量、刚度和非对称非经典阻尼矩阵结构响应的精确实空间解耦及其基于反应谱的地震作用取值的一般解析分析。

[1]周福霖. 工程结构减震控制[M]. 北京：地震出版社，1997.

[2]刘彦辉，杜永峰，周福霖. 高层剪力墙复合基础隔震结构地震响应分析[J]. 工程力学，2011，28(7)：143-150.

LIU Yan-hui, DU Yong-feng, ZHOU Fu-lin. Seismic response analysis of composite base-isolated tall shear wall buildings[J]. Engineering Mechanics, 2011, 28(7): 143-150.

[3]潘东辉，于国有，张德强. 隔震高层结构的悬臂梁模型的地震反应研究[J]. 工程力学，2012，29(5)：115-211.

PAN Dong-hui, YU Guo-you, ZHANG De-qiang. Earthquake response analysis of cantilever-beam model of isolated high-rise structure[J]. Engineering Mechanics, 2012, 29(5): 115-211.

[4]Hwang T S, Chang K C, Tsai M H. Composite damping ratio of seismically isolated regular bridge [J]. Engineering Structures, 1997, 19(1): 52-62.

[5]李中锡，周锡元. 规则型隔震房屋的自振特性和地震反应分析方法[J]. 地震工程与工程振动，2002，22(2)：33-41.

LI Zhong-xi,ZHOU Xi-yuan.The simplified analysis method of seismically base isolated regular buildings[J]. Earthquake Engineering and Engineering Vibration, 2002，22(2): 33-41.

[6]Kelly J M. The role of damping in seismic isolation [J]. Earthquake Engineering and Structural Dynamics, 1999, 28: 3-20.

[7]杜永峰，赵国藩. 隔震结构中非经典阻尼影响及最佳阻尼比分析[J]. 地震工程与工程振动，2000，20(3)：100-107.

DU Yong-feng, ZHAO Guo-fan. Analysis of effect of non-classical damping on isolated structure and optimum damping[J]. Earthquake Engineering and Engineering Vibration, 2000, 20(3): 100-107.

[8]杜永峰，李慧，苏磐石，等. 非比例阻尼隔振结构地震响应的实振型分解法[J]. 工程力学，2003，20(4)：24-32.

DU Yong-feng, LI hui ,SU Pan-shi, et al. Real mode superposition method for analysis of seismic response of non-proportionally damped isolated structures[J].Engineering Mechanics，2003，20(4)：24-32．

[9]王光远 等译校. 结构动力学(第二版)[M]. 北京：高等教育出版社，2006.

[10]Tong M, Liang Z, Lee G C. An index of damping non-proportionality for discrete vibrating systems [J]. Journal of Sound and Vibration, 1994, 174(1): 37-55.

[11]Liu K, Kujath M R, Zheng W. Quantification of non-proportionality of damping in discrete vibratory systems [J]. Computers and Structures, 2000, 77: 557-568.

[12]Morzfeld M, Ajavakom N, Ma F. A remark about the decoupling approximation of damped linear systems [J]. Mechanics Research Communica-tions, 2008, 35(7): 439-446.

[13]Morzfeld M, Ajavakom N, Ma F. Diagonal dominance of damping and the decoupling approximation in linear vibratory systems [J]. Journal of Sound and Vibration, 2009, 320: 406-420.

[14]Cacciola P, Colajanni P, Muscolino G. Combination of model responses consistent with seismic input representation [J]. Journal of Structural Engineering, 2004, 130(1): 47-55.

[15]方同. 工程随机振动[M]. 北京：国防工业出版社，1995.

[16]陈欧阳. 非对称非经典结构实空间解耦和地震作用取值方法及其在多高层隔震结构中应用[D]. 南宁:广西大学,2013.

[17]李创第，陈俊忠，黄东梅. 多自由度“加层”减震结构地震作用取值的复模态法[J]. 哈尔滨工业大学学报，2009，41(4)：201-203.

LI Chuang-di, CHEN Jun-zhong, HUANG Dong-mei, Ge Xin-guang. Methods of earthquake action calculation for MDOF structure with TMD and the add-layer[J]. Journal of Harbin Institute of Technology, 2009, 41(4): 201-203.

[18]Lin Y Y, Chang K C. Study on damping reduction factor for buildings under earthquake ground motions [J]. Journal of Structural Engineering, 2003, 129(2): 206-214.

[19]高小旺，龚思礼，苏经守等. 建筑抗震设计规范理解与应用[M]. 北京：中国建筑工业出版社，2005.

[20]沈聚敏，周锡元，高小旺等. 抗震工程学[M]. 北京：中国建筑工业出版社，2000.