基于有限元法的贴敷阻尼薄板声辐射性能研究

闫兆敏，张东俊, 温激鸿，温熙森

(1.声学与振动研究组 装备综合保障技术重点实验室 国防科技大学,长沙 410073；2.海军92337部队，大连 116023)

薄板及由其组成的复杂结构凭借良好的工程性质，在机械、船舶与航空等领域得到了广泛的应用，工程中的许多结构都是由薄板的典型结构组成，各国学者很早就开展了对其振动与声辐射问题的研究。阻尼减振降噪技术(简称阻尼技术)是控制结构振动和声辐射的一项重要技术，其原理是在结构表面贴敷阻尼材料，将结构的振动能转化为热能耗散从而达到减小振动和声辐射的目的，在实际工程中经常通过铺设多层性质不同的阻尼材料进一步增强阻尼减振降噪的效果[1]。

铺设阻尼材料的薄板结构可作为复合材料层合板结构来进行研究。根据复合材料层合结构的特点，对层合板动态性能的求解常常需要利用一些物理假设来构建位移方程。根据位移方程的不同，层合板理论主要可分为经典层合板理论(Classical Lamination Theory, CLD)[2-3]、一阶剪切变形理论(First-Order Shear Deformation Theory, FSDT)[4]、高阶剪切变形理论(Higher-Order Shear Deformation Theory, HSDT)[5-6]、分层理论(Layerwise Theory)[7-9]和三维弹性理论(3-D Elasticity Theory)[10]，Khandan等[11]对层合板理论的发展历程进行了综述。分层理论可看作是一种准三维弹性理论，其在板的厚度方向利用插值函数来描述每层内位移沿厚度方向的变化规律，结合有限元法可凭借较小的计算开销取得较好的计算精度，因而具有广泛的适用性。

目前，许多学者已对贴敷单层阻尼的结构振动与声辐射问题开展了广泛的研究[12-15]，而对贴敷多层阻尼结构以及流动流体中贴敷阻尼结构的振动和声辐射问题研究较少,与此同时，分层理论主要应用于单层板壳结构的振动特性分析[7-9]，将其应用于多层板壳结构声辐射分析的研究也不常见。本文采用分层理论建立了四边简支约束条件下薄板声辐射特性有限元模型，计算了其固有频率、辐射声功率以及振动均方速度，并与Comsol软件计算结果进行对比，证明了该方法的有效性。其次，将分层理论拓展运用于贴敷阻尼薄板的声辐射性能研究中，分析了单/多层阻尼对结构声辐射的影响规律。最后通过分析贴敷阻尼薄板在轻/重流体、不同流速条件下的声振特性，研究流体对贴敷阻尼薄板声辐射性能的影响，为薄板结构贴敷阻尼以降低声辐射水平奠定了理论基础。

1 理论模型

1.1 基于分层理论的有限元模型

薄板贴敷多层黏弹性阻尼材料形成的层合板如图1所示。

根据分层理论，可将各层阻尼沿厚度方向进行人为插值。以第k阻尼层为例，其沿x,y,z方向的位移可表示为[8]：

(1)

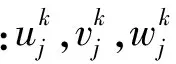
(2)

(3)

式中:n表示平面的节点数，Ni表示i节点的平面插值形函数。将式(3)代入式(1)可得：

(4)

由式(4)可以发现，分层理论将三维结构的位移利用二维平面的位移来表示的同时也考虑了厚度方向各层之间的连接关系。

1.2 结构声辐射模型

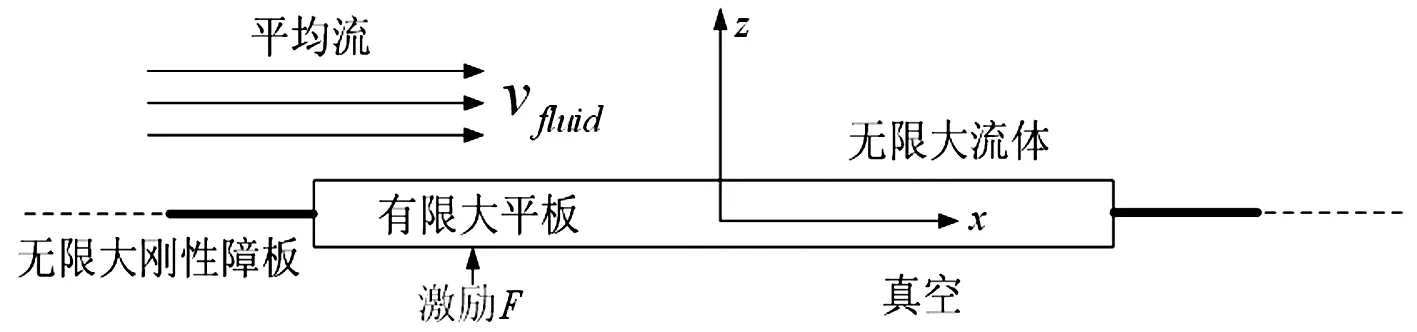
图2 声辐射模型示意图

声辐射模型如图2所示，有关流体声学负载的计算，文献[16-17]给出了详细的推导过程，结构表面上一点M的声压可表示为

(5)

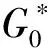
(-ω2M+iω(C+GAZGT)+K)w=f

(6)

值得注意的是，当考虑流体的流速时，式(5)只在较低的频段内有效[16]。

当求得结构表面的声压和法向振速后，结构的辐射声功率可通过下式求得

(7)

式中:M是属于面S上的一点，Re表示取实部，p(M)表示M点处的声压，un(M)表示M点处的法向振速，“*”表示复数共轭。

当结构发生振动时，结构会向周围流体介质进行压缩产生声波，声波通过流体介质向远场辐射，形成声辐射。声辐射阻尼用以表征流体将振动能转化为声能的能力，其定义为[19]：

μf=ER/ES=WT/ES=2πW/ESω

(8)

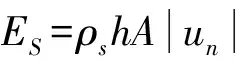
2 数值计算与分析

2.1 数值算例

固有模态频率是结构的重要参数，为验证前述分层模型的准确性，构建四边简支约束矩形薄板模型，其物理参数见表1。

表1 薄板物理参数

通过前述分层模型理论求得的结构前5阶固有频率与Comsol软件及文献结果对比如表2所示：

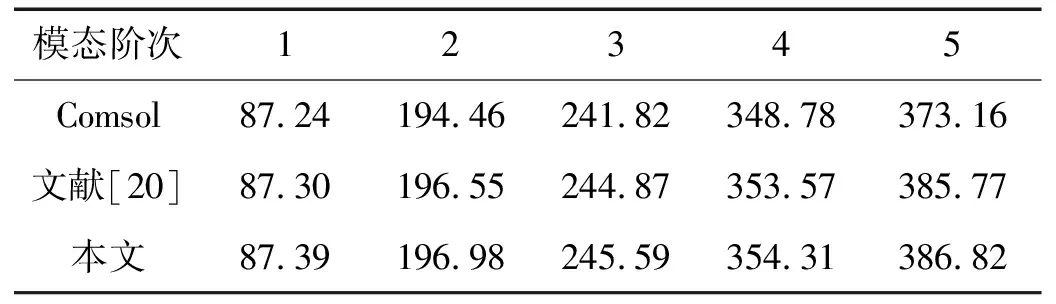
表2 四边简支层合板结构前5阶固有频率对比(单位：Hz)

在四边简支边界条件下，基于分层理论的有限元法与商用有限元软件及文献计算结果吻合度较高。此外，若沿Z方向施加简谐激励力F施加于(0.113 75,0.094 75,0)处，幅值为1 N，激励频率范围为10-1 000 Hz，分别利用分层理论有限元法与Comsol计算在空气介质中(空气的密度为1.225 kg/m3，声速为344 m/s)的薄板辐射声功率与振动均方速度结果对比如图3所示，由结果可以发现，分层理论所得结果与商用有限元软件结果较吻合，从而证明了利用该方法能够较准确地计算出结构的声振特性。

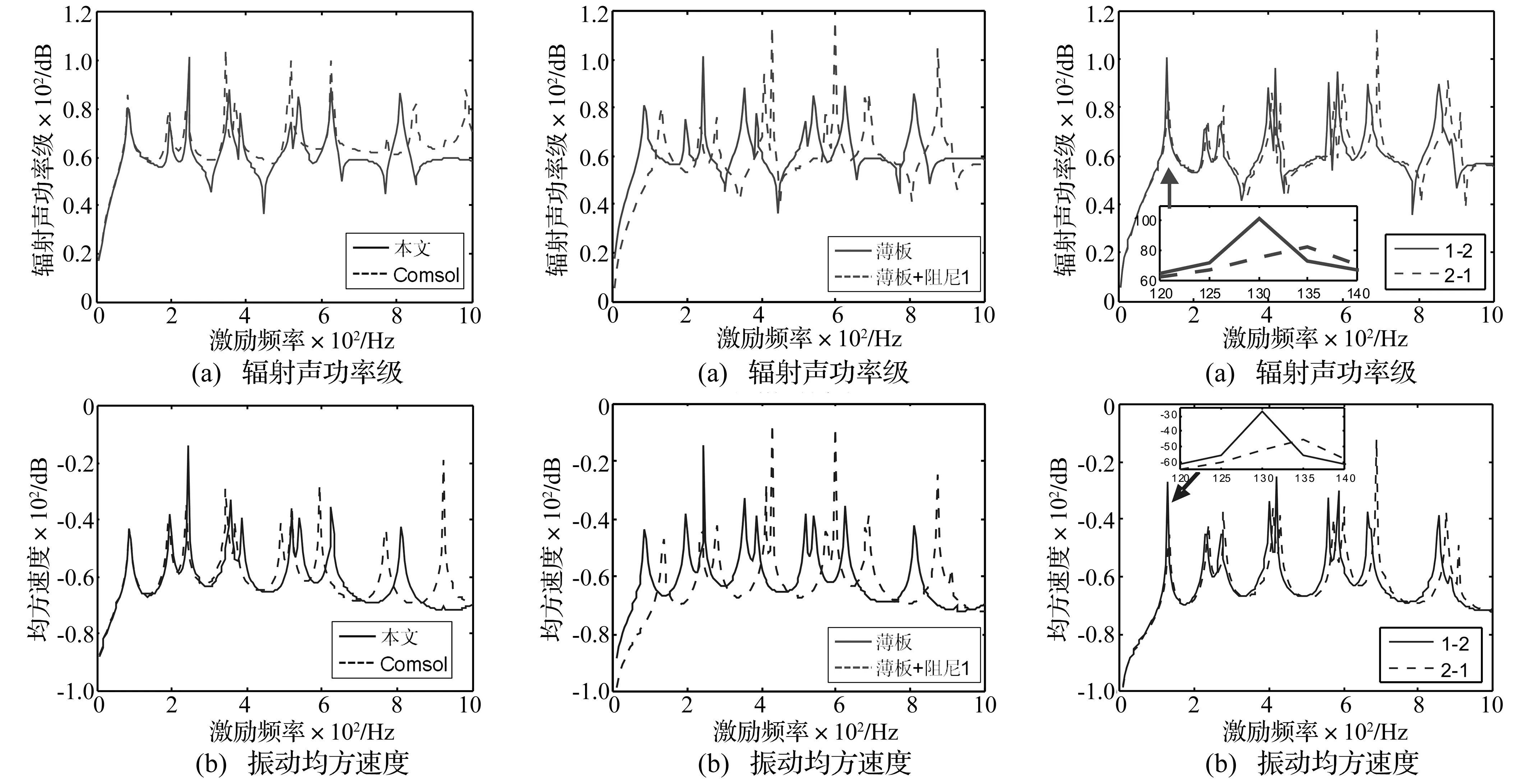
图3 结构声辐射特性对比

2.2 贴敷单/多层阻尼对薄板声辐射的影响

以前述薄板结构为研究对象，在其表面贴敷阻尼材料以抑制其结构声辐射，阻尼材料特性如表3所示。

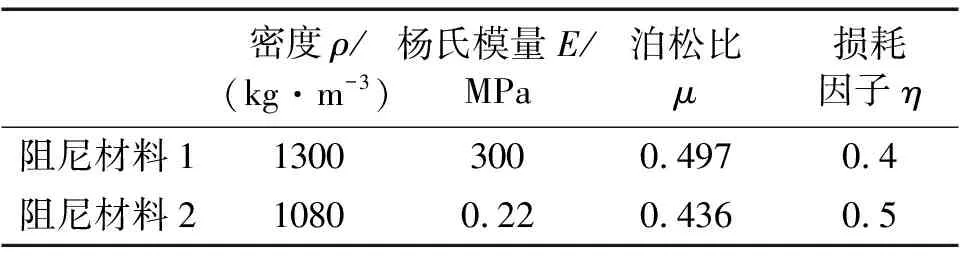
表3 阻尼层材料物理参数

将厚度为6 mm的阻尼材料1均匀贴敷在薄板结构表面，结构周围为空气介质，计算得到薄板结构的声辐射特性如图4所示。

从图中可以发现，贴敷阻尼材料后，结构的等效刚度、等效密度以及等效阻尼等参数发生变化，使得结构的辐射声功率级峰值频率向高频方向移动，在10-1 00 Hz范围内的辐射声功率和振动均方速度均下降了约10 dB，效果显著，由此说明贴敷阻尼材料对抑制薄板振动和声辐射具有较明显的作用。

进一步对表面贴敷不同种类阻尼组合而成的阻尼材料的结构声辐射特性进行探讨。以两层阻尼结构为例，将表3中的两种阻尼材料进行组合，构成混合阻尼贴附在前述薄板结构表面，每种阻尼层的厚度均为3 mm，此时共有2种贴敷方式，沿Z轴正方向排序，可将这2种贴敷方式按材料种类依次表示为1-2、2-1，外部激励F与前述相同,计算结果如图5所示。

由图5可以看出，贴敷两层阻尼的薄板结构声辐射特性对阻尼材料的贴敷顺序较为敏感。以第1阶辐射峰为例，2-1贴敷方式下的辐射声功率级和振动均方速度与1-2贴敷方式相比均降低了约20 dB，效果显著，说明将弹性模量较大的阻尼材料贴敷在结构靠外侧更有利于减小结构的振动和声辐射。这是因为将弹性模量较大的阻尼材料贴敷在靠外侧可以与内侧弹性模量较小的阻尼材料构成约束阻尼，当结构受到振动而发生弯曲变形时，内侧模量较小的阻尼层受上下两个约束面的作用而不能有伸缩变形，各层之间发生剪切变形耗能，同时，外层阻尼还可作为自由阻尼层，利用交变的应力和应变来消耗振动能量，这样可提高结构整体的损耗因子，进一步减小结构的振动，从而抑制声辐射。

2.3 流体对贴敷阻尼层薄板声辐射的影响

以2.2节所述贴敷单层阻尼薄板为研究对象，分别讨论结构在轻、重流体中的声振特性(本文以空气作为轻流体，水作为重流体)，结果如图6所示，由图中可以发现流体对结构声辐射性能有重要的影响。相比于轻流体，结构在重流体中的模态频率向低频方向移动，振动均方速度显著降低，而辐射声功率则明显升高，这是由于流固耦合作用对结构引入了附加质量，而重流体所引入的附加质量远远高于轻流体，因此出现结构在重流体中的模态频率向低频方向移动，且振动受到明显抑制。此外，重流体的密度和声速较高，使得重流体的辐射声阻抗较高，在较小振动的条件下能够引起较高的声压，从而使得其辐射声功率高于轻流体。

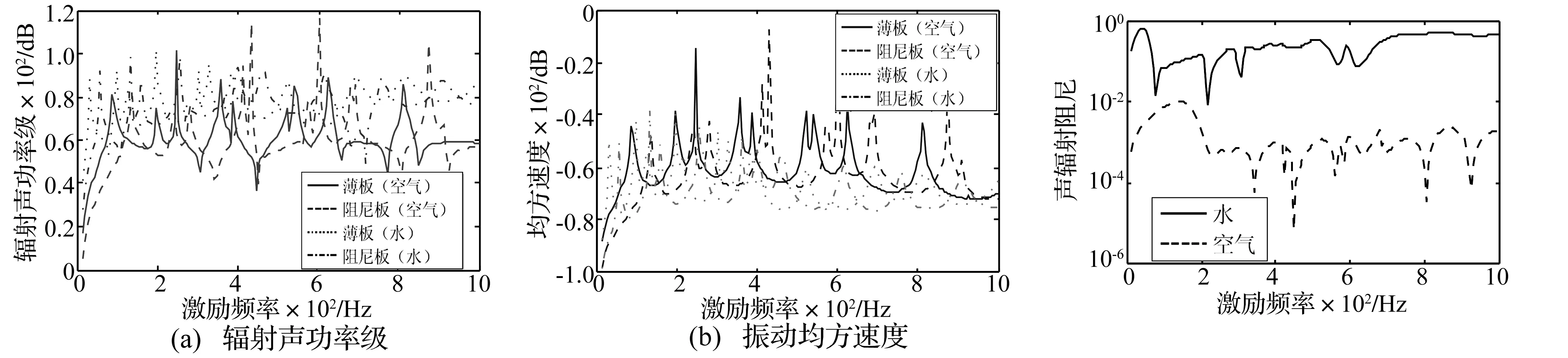
图6 轻/重流体介质中结构声辐射特性

比较轻/重流体中的结构声辐射情况还可以发现，在重流体中的辐射声功率以及振动均方速度曲线更为平缓，结构阻尼效果更加明显。通过比较两种流体介质的声辐射阻尼(如图7所示)可以发现，水中的声辐射阻尼远远大于空气，结构在水中所受的阻尼效果远大于在空气中的效果，因此会出现两条曲线更为平缓的现象。

除流体的密度和声速外，流体流速也是影响结构声辐射的重要因素。前述贴敷单层阻尼薄板在不同流速重流体中的声辐射情况如图8所示，随着流体流速的增大，结构的辐射峰向低频方向移动，振动和声辐射均有增大的趋势，在峰值处的幅值变化更加平缓，且流速主要在非峰值频率段的结构声辐射以及峰值频率段的结构振动方面产生较大影响，通过式(5)可知产生这种现象的主要原因是流体流动时会引入了负刚度和附加阻尼，改变结构的动态力学参数，从而使结构声辐射性能发生变化。此外，由图8还可以发现流体流速对结构声辐射的影响是非线性的，以 10 Hz处的辐射声功率及振动均方速度为例，其变化趋势如图9所示，当流速较低时，结构的声振特性变化明显，此后，随着流体流速的增大，结构的声振特性也趋于平稳。

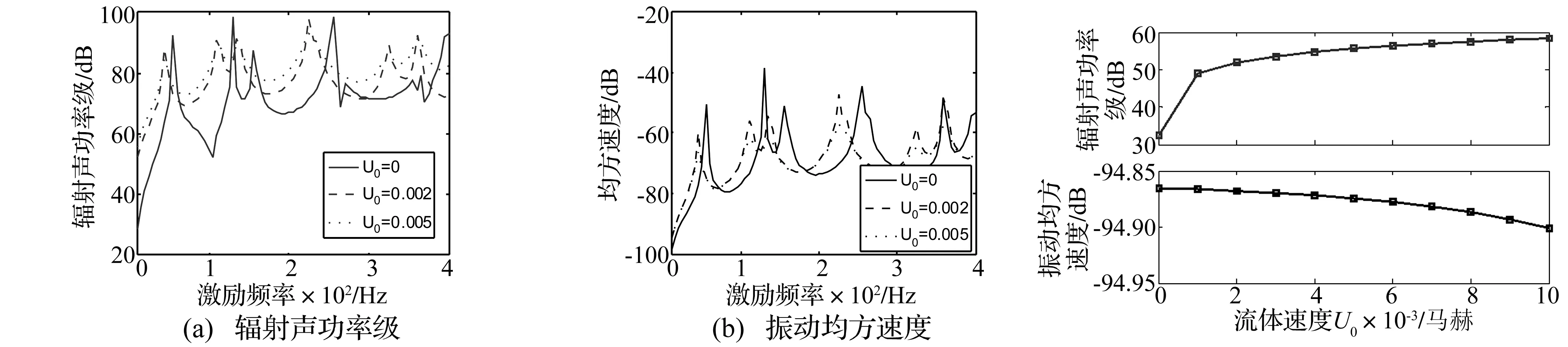
图8 不同流速流体中结构声辐射特性

3 结 论

本文基于分层理论建立了四边简支约束条件下贴敷阻尼薄板声振特性有限元分析模型，计算了其固有频率、辐射声功率以及振动均方速度，并与Comsol软件计算结果进行对比，证明了该方法用于分析结构声振特性的有效性。其次，将分层理论用于贴敷阻尼薄板的声辐射性能研究中，分析了单/多层阻尼对结构声辐射的影响规律。最后，通过分析贴敷阻尼薄板在不同流体介质、不同流速条件下的声振特性，研究了流体对贴敷阻尼薄板声辐射性能的影响。结果表明：

(1) 贴敷阻尼材料对结构等效密度、等效刚度以及等效阻尼影响显著，通过贴敷阻尼后可使薄板在第1阶峰值频率处的辐射声功率和振动均方速度降低约10 dB。贴敷多层阻尼的薄板结构声辐射特性对阻尼材料的贴敷顺序较为敏感，将弹性模量较大的阻尼材料贴敷在靠外侧能够增大约束阻尼层的剪切变形，有利于提高结构整体的损耗因子，降低结构的振动和声辐射。

(2) 流固耦合会对结构产生附加阻尼作用，进一步加强阻尼层的贴敷效果，使得结构声振特性变化更为平缓。结构在重流体介质中的振动受到抑制，但由于重流体介质中的声辐射阻尼较大，导致结构在重流体中的辐射声功率远高于轻流体。

(3) 由于流体流速引入负刚度和附加阻尼作用，因而会使结构声振特性发生较大变化且变化为非线性，当流速较低时，结构的声振特性变化明显，此后，随着流体流速的增大，结构的声振特性趋于平稳。

[1]何作镛. 结构振动与声辐射[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001.

[2]Petyt M. Introduction to finite element vibration analysis[M]. 2nd ed. New York: Cambridge University Press, 2010.

[3]Parthasarathy G, Reddy C V R. Partial coverage of rectangular plates by unconstrained layer damping treatments[J]. Journal of Sound and Vibration,1985, 102: 203-216.

[4]Bhar A, Phoenix S S, Satsangi S K. Finite element analysis of laminated composite stiffened plates using FSDT and HSDT: A comparative perspective[J]. Composite Structures,2010, 92: 312-321.

[5]Xiang S, Jiang S, Bi Z, et al. A nth-order meshless generalization of Reddy’s third-order shear deformation theory for the free vibration on laminated composite plates[J]. Composite Structures,2011, 93(2011): 299-307.

[6]Kumar J S, Raju T D, Reddy K V K. Vibration analysis of composite laminated plates using higher-order shear deformation theory with zig-zag[J]. Indian Journal of Science and Technology,2011, 4(8): 960-966.

[7]Desai Y M, Ramtekkar G S, Shah A H. Dynamic analysis of laminated composite plates using a layer-wise mixed finite element model[J]. Composite Structures,2003, 59(2): 237-249.

[8]Reddy J N. Mechanics of laminated composite plates and shells: theory and analysis[M]. 2nd ed. Boca Raton: CRC PRESS, 2003.

[9]胡明勇，王安稳. 纤维增强粘弹性复合材料层合板的自由振动和应力分析[J]. 工程力学,2010, 27(8): 10-20.

HU Ming-yong, WANG An-wen. Free vibration and stresses analysis of fiber-reinforced viscoelastic composite laminated plates[J]. Engineering Mechanics, 2010, 27(8):10-20.

[10]Reddy J N. Theories and computational models for composite laminate[J]. Applied mechanics reviews,1994, 47(6): 147-169.

[11]Khandan R, Noroozi S, Sewell P, et al. The development of laminated composite plate theories:a review[J]. Journal of Material Science, 2012, 47: 5901-5910.

[12]Laulagnet B, Guyader J L. Sound radiation from finite cylindrical coated shells, by means of asymptotic expansion of three-dimensional equations for coating[J]. J.Acoust.Soc.Am,1994, 96(1): 277-286.

[13]Laulagnet B, Guyader J L. Sound radiation from finite cylindrical shells partially covered with longitudinal strips of compliant layer[J]. Journal of Sound and Vibration,1995, 186(5): 723-741.

[14]王献忠，孙龙泉，邱忠辉，等. 部分敷设阻尼材料的水下结构声辐射分析[J]. 振动与冲击, 2012, 31(18): 122-127.

WANG Xian-zhong, SUN Long-quan, QIU Zhong-hui, et al. Sound radiation analysis for a submerged structure with a viscoelastic damping layer partially covered[J]. Journal of Vibration and Shock,2012,31(18): 122-127.

[15]陈美霞，骆东平，周峰，等. 阻尼材料敷设方式对双层壳体声辐射性能的影响[J]. 声学学报, 2005, 30(4): 296-301.

CHEN Mei-xia, LUO Dong-ping, ZHOU Feng, et al. Effect of viscoelastic layer cover type on characteristics of sound radiation from double cylindrical shell[J]. Acta Acustica, 2005, 30(4):296-301.

[16]Atalla N, Nicolas J. A Formulation for mean flow effects on sound radiation from rectangular baffled plates with arbitrary boundary conditions[J]. Journal of Vibration and Acoustics,1995, 117: 22-29.

[17]Sgard F, Atalla N, Nicolas J. Coupled FEM-BEM approach for mean flow effects on vibro-acoustic behavior of planar structures[J]. AIAA Journal,1994, 32(12): 2351-2358.

[18]姜弘道. 弹性力学问题的边界元法[M]. 北京: 中国水利水电出版社, 2008.

[19]郭新毅，洪明. 结构振动声辐射阻尼研究[J]. 中国造船,2004, 45: 189-196.

GUO Xin-yi, HONG Ming. Research on acoustic radiation damping by structual vibration[J]. Shipbuilding of China,2004,45:189-196.

[20]黎胜. 水下结构声辐射和声传输的数值分析及主动控制模拟研究[D]. 大连: 大连理工大学, 2001.