板结构-声场耦合分析的FE-LSPIM/FE-LSPIM法
陈 宁, 于德介, 吕 辉, 夏百战
(湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082)
几乎所有的声学问题都与结构-声场耦合系统有关,因此对结构-声场耦合系统的研究具有重要的工程意义。结构-声场耦合系统的分析能为结构件的优化提供重要信息,特别是容易受到声压激励而产生振动的弹性薄壁结构件。板结构-声场耦合系统包含板结构域、声场域和两个域之间的耦合作用。通常,在结构域用位移描述结构的状态,在声场域用声压描述声场的状态[1-2]。
目前,有限元/有限元法(Finite Element Method, FEM)和有限元(FEM)/边界元法(Boundary Element Method, BEM)是分析结构-声场耦合系统最常用的数值计算方法。FEM/ BEM与FEM/ FEM相比,能减少模型的单元数量,但其矩阵为非稀疏矩阵,并不一定能提高计算效率;而对于内声场问题,FEM/ FEM 计算效率往往更高一些;同时两者的计算结果受模型网格尺寸影响较大,因此FEM/ FEM 和FEM/ BEM 主要用于求解中低频的结构-声场耦合 问题[3-4]。Yao等[4]提出的SFEM(Smoothed Finite Element Method)/FEM方法在结构-声场耦合问题的分析中能取得比FEM/FEM更高的精度。
有限元法虽然得到了广泛的应用,但仍存在一些不足,如等参单元对于网格几何变形非常敏感,为了获得可靠的计算结果,通常需要更精细的网格等。无网格法则有效地避免了有限元的一些缺点,具有精度高、 计算模型不需划分网格等特点,但无网格法本身存在诸多缺陷,如其形函数不具备克罗内克尔性质,导致不能直接施加边界条件、计算效率降低等。针对有限元法和无网格技术的特点,Melenk等[5-6]结合有限元和无网格技术,提出了混合有限元-无网格法来分析各类力学问题。其中,单位分解有限元法是一种常用的混合有限元-无网格方法,该方法的基本原理是在不增加支撑点的前提下,通过增加局部支撑函数的阶次来构造高阶的全局有限元公式。Zhang等[7-8]提出了一种基于单位分解的有限元-最小二乘点插值法(Finite Element-Least Square Point Interpolation Method,FE-LSPIM),该方法采用的有限元-无网格四边形单元将有限元形函数和最小二乘点插值形函数相结合,综合了有限元法和无网格法各自的优点,其形函数具有克罗内克尔性质,具有单元兼容性以及高阶完备性,并且成功地应用于静力学和动力学分析中。随后姚凌云等[9]将FE-LSPIM推广到二维声场的研究之中,并取得了良好的效果。
为了提高结构-声场耦合分析精度,降低结构-声场耦合分析中对结构网格尺寸的要求,本文将FE-LSPIM推广到板结构动力学和三维声场的分析中,提出用于板结构-声场耦合问题分析的FE-LSPIM/FE-LSPIM。运用FE-LSPIM/FE-LSPIM分析板结构-声场耦合问题时,板结构域采用有限元-无网格四边形单元,声场域采用有限元-无网格六面体单元。以一个六面体板结构-声场耦合模型为数值算例进行分析,结果表明,FE-LSPIM/FE-LSPIM继承了FE-LSPIM适用性好、精度高的特点。与FEM/ FEM和SFEM/ FEM相比,FE-LSPIM/FE-LSPIM的精度更高,对网格尺寸的质量要求更低,能很好地应用于板结构- 声场耦合分析,具有良好的工程应用前景。
1 基于FE-LSPIM/FE-LSPIM的板结构动力学分析
1.1 板单元的有限元-最小二乘点插值
根据剪切变形理论,如图1所示,明德林-瑞斯纳 (Mindlin-Reissner)板模型的位移分量u,v分别表示为:
u=-wθx(x,y)
v=-wθy(x,y)
(1)
式中:u,v,w分别为板中面x,y,z三个方向的位移,θx和θy分别为xz和yz平面内的转角。定义弯曲应变为κ,剪切应变为γ,有:
(2)
板结构的横向剪切刚度本构矩阵Ds和弯曲刚度本构矩阵Db分别可表示为:
(3)
式中,E为弹性模量;t为板单元厚度;ν为柏松比;μ为剪切修正系数[1]。
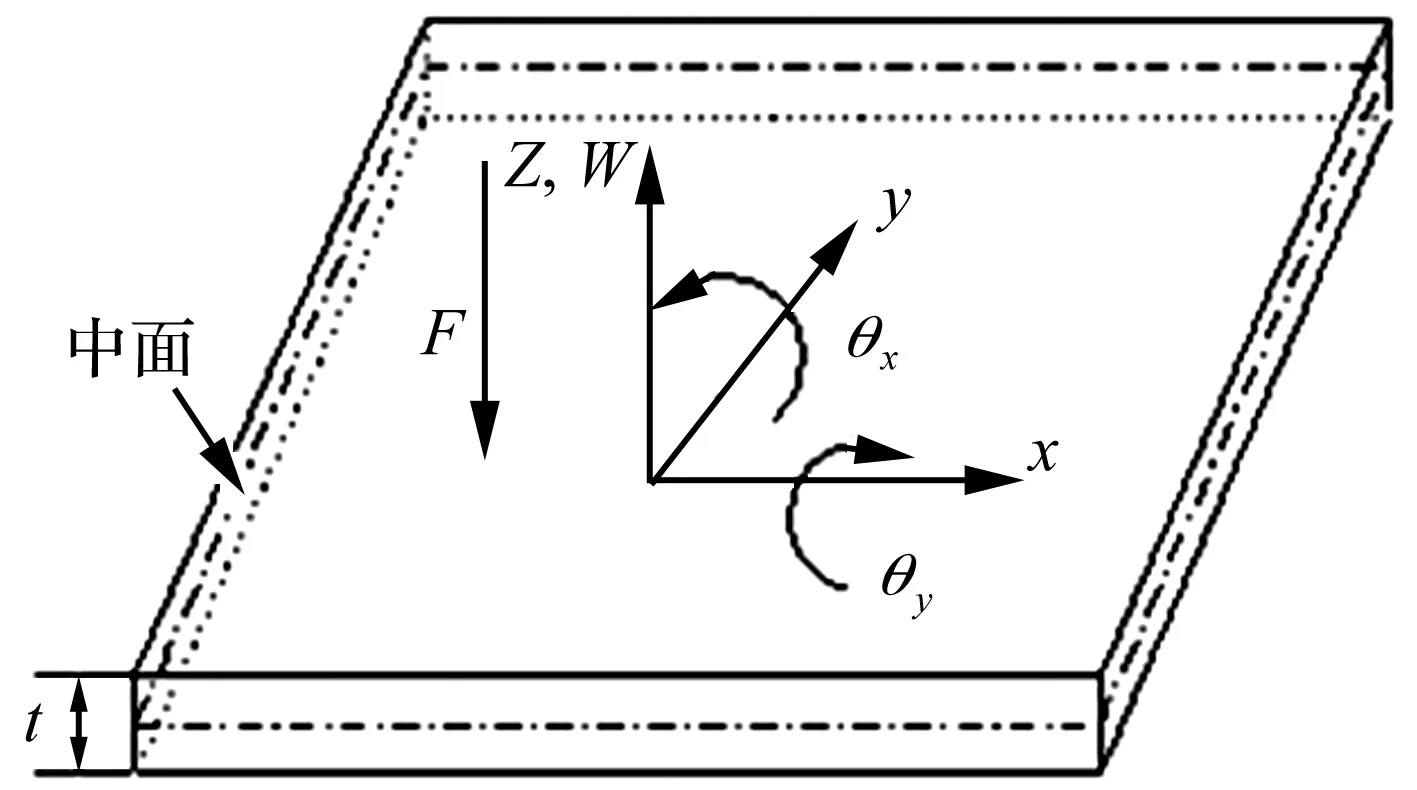
图1 板单元示意图
根据标准的有限元法,对板结构域Ω进行离散,四边形单元数为Ne,节点数为Nd。对于板单元,广义位移u={θxθyw}T是各自独立插值的,其表示为:
u(x,y)=Nplateue
(4)
式中:Nplate为四边形板单元形函数,ue为节点的位移,可以写成:
(I=1,2,3,4)
(5)
ue={u1(x,y)u2(x,y)u3(x,y)u4(x,y)}T
ui(x,y)={θxiθyiwi}T(i=1,2,3,4)
(6)
节点位移函数ui(x,y)由支撑节点通过LSPIM插值得到。以广义位移中的挠度对整个求解过程进行推导,挠度w(x,y)可表示为:
w(x,y)=NIwe
(7)
向量we表示对应的四边形单元四个节点的挠度近似函数wi(x,y)(i=1,2,3,4),可表示为:
we={w1(x,y)w2(x,y)w3(x,y)w4(x,y)}T
(8)
其中挠度wi(x,y)(i=1,2,3,4)可表示为:
wi(x,y)=Φiwi(i=1,2,3,4)
(9)
wi=[w1w2w3…wn]T
(10)
式中,Φi为节点i的LSPIM形函数,它由节点i的支撑域点通过LSPIM构成;wi为支撑节点的挠度向量函数;n为节点i的支撑域点的个数。
矩阵Φ4×M由Φi(i=1, 2, 3, 4)组装得到,列数M等于单元支撑域的节点数。节点支撑域Ω1={1, 2, 3, 4, 5, 6, 7, 8, 9},Ω2={1, 2, 3, 4, 8, 9, 10, 11, 12},Ω3={1, 2, 3, 4, 11, 12, 13, 14, 15} ,Ω4={1, 2, 3, 4, 5, 6, 14, 15, 16};单元支撑域Ω=Ω1⊕Ω2⊕Ω3⊕Ω4={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12, 13, 14, 15, 16},如图2所示。
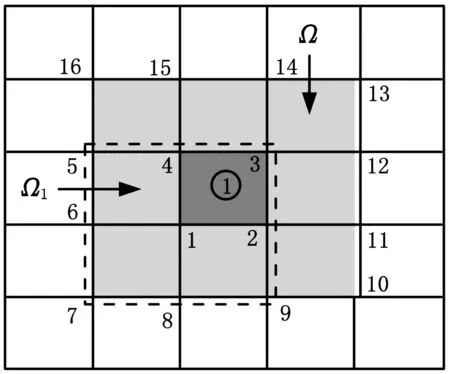
图2 节点及单元支撑域定义
将式(10),式(9),式(8)代入式(7)中,得到四边形单元内场点挠度变量的近似形式为:
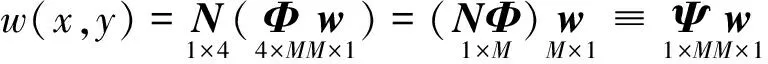
(11)
式中,Ψ为FE-LSPIM的形函数矩阵,定义为:
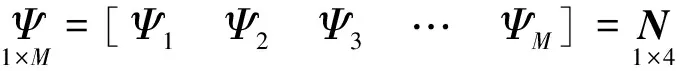
(12)
同理,转动θx和θy可分别表示为:
(13)
1.2 板的动力学方程
无阻尼板结构动力学方程的Galerkin弱形式为:
∫ΩδκTDbκdΩ+∫ΩδγTDsdΩ+
(14)
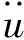
离散后板结构的动力学方程为:
(15)
式中,K=Kb+Ks为板单元刚度矩阵;Kb为弯曲刚度矩阵,Ks为剪切刚度矩阵,M为板单元质量矩阵,Fb为体积力列阵。
刚度矩阵K可表示为:
K=Kb+Ks=
∫Ω(Bb)TDbBbdΩ+∫Ω(Bs)TDsBsdΩ
(16)
式中:
(17)
质量矩阵M可表示为:
(18)
载荷矢量可表示为:
Fb=∫ΩQTbdΩ
(19)
2 板结构-声场耦合分析
2.1 声场有限元-最小二乘点插值模型
板结构振动在理想声场介质中引起的小振幅简谐声波、声压满足Helmholtz波动方程:
2p+k2p=0
(20)
式中,p为声压;k为波数,k=ω/c;ω为圆频率;c为声速。
根据伽辽金原理,声场问题的弱形式可以写成如下形式:
∫Ωδp·
(21)
式中,qf表示单位体积的附加载荷。
按照FEM方式将声场域离散为六面体网格,节点声压值近似写成:
(22)
式中,m为离散单元的节点个数,Nf为标准有限元流体单元的形函数,向量p为六面体单元8个节点的声压近似函数pi(x,y)(i=1,2,…,8)。节点声压函数pi(x,y)由支撑节点通过LSPIM插值得到,其支撑域范围如图3所示。其插值过程与板单元的有限元-最小二乘插值相同,在此不再赘述。

图3 六面体单元节点i的支撑域点
有限元-最小二乘插值得到的六面体单元内的声压近似函数为:
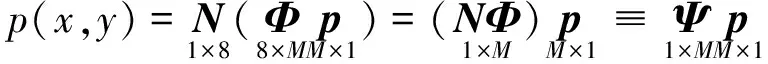
(23)
将式(22)代入(21)中,得到系统的离散方程:
p={p1,p2,…,pn}T
Fs=ρ∫ΩsfΨTΨdΓ
(24)
式中,Kf为声学刚度矩阵,Bf为声学梯度矩阵,Mf为声学质量矩阵,p为节点的声压矢量,Fs为载荷向量。
2.2 结构-声场耦合模型
为实现结构FE-LSPIM模型和声场FE-LSPIM模型的耦合,如图4所示,在板结构与声场的交界面即耦合界面上,应满足位移和压力连续的条件。引入界面法向矢量n=nf=-ns,位移连续条件和压力连续条件可表示为:
(25)
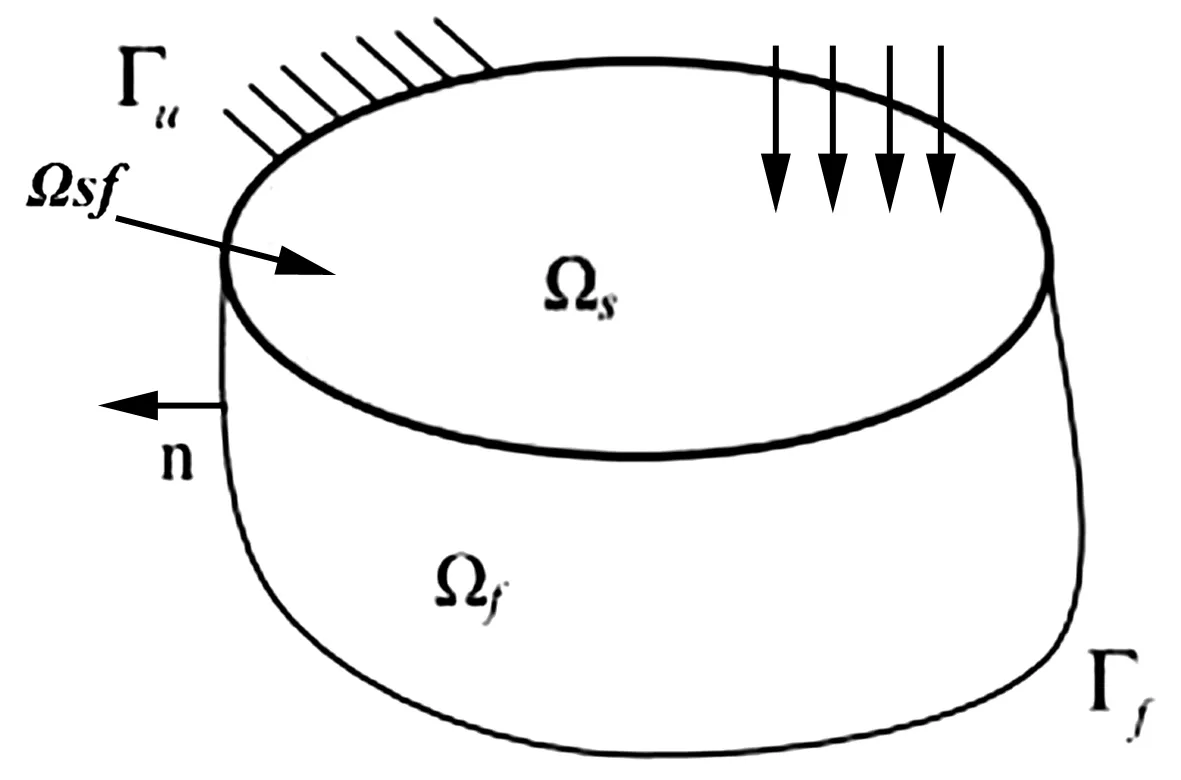
图4 板结构-声场耦合系统示意图
根据式(24),结构作用在声场耦合界面Ωsf上的载荷Fs为:
(26)
根据式(19),声场作用在结构耦合界面Ωsf上的载荷Ff为:
(27)
式中Ns为结构域单元的形函数,Nf是声场单元的形函数,这里都采用四边形等参单元的形函数。
引入耦合矩阵L:
(28)
从结构域的FE-LSPIM模型和声场的FE-LSPIM模型,可得到结构-声场耦合的FE-LSPIM/ FE-LSPIM模型:
(29)
假设位移和声压为整个时域上的谐波,上式可以写成:
(30)
3 数值算例

图5 带矩形板的六面体结构-声场耦合模型
图5所示为六面体附带矩形板的结构-声学耦合模型,尺寸为0.414 m×0.314 m×0.360 m。六面体内为空气域,下表面为矩形平面板结构,尺寸0.414 m×0.314 m,板四边简支,其它表面为刚性边界。矩形平面板材料参数为:弹性模量E=71 GPa,泊松比ν=0.3,密度ρs=2 700 kg/m3,板结构厚度为0.001 m。空气域声学参数为:密度ρf=1.21 kg/m3,声速c=343 m/s。施加在矩形平面板中心点+Z方向的简谐激励力幅值为1 N。
本文计算结构-声场耦合系统问题均通过Matlab程序实现。因为有限元方法网格越密结果越准确,所以参考值通过FEM方法计算较密的网格得到。将平板结构域和声场域耦合平面按不同网格密度划分成节点均匀分布的四边形网格,不同耦合平面网格密度下的结构域和声域单元数目与单元类型如表1所示。
表1 六面体模型的网格划分
首先应用FE-LSPIM计算矩形弹性板的特征频率值,并与SFEM和FEM进行对比研究。将矩形弹性板离散成网格密度为8×8的网格模型,用FE-LSPIM、SFEM和FEM分别求得矩形弹性板的前14阶固有频率值,结果如表2所示。表2中参考值由文献[1]得到。从表2中可以看出,SFEM所得结果略优于FEM所得结果;除了第一阶特征频率外,FE-LSPIM所得结果明显优于SFEM和FEM所得结果。
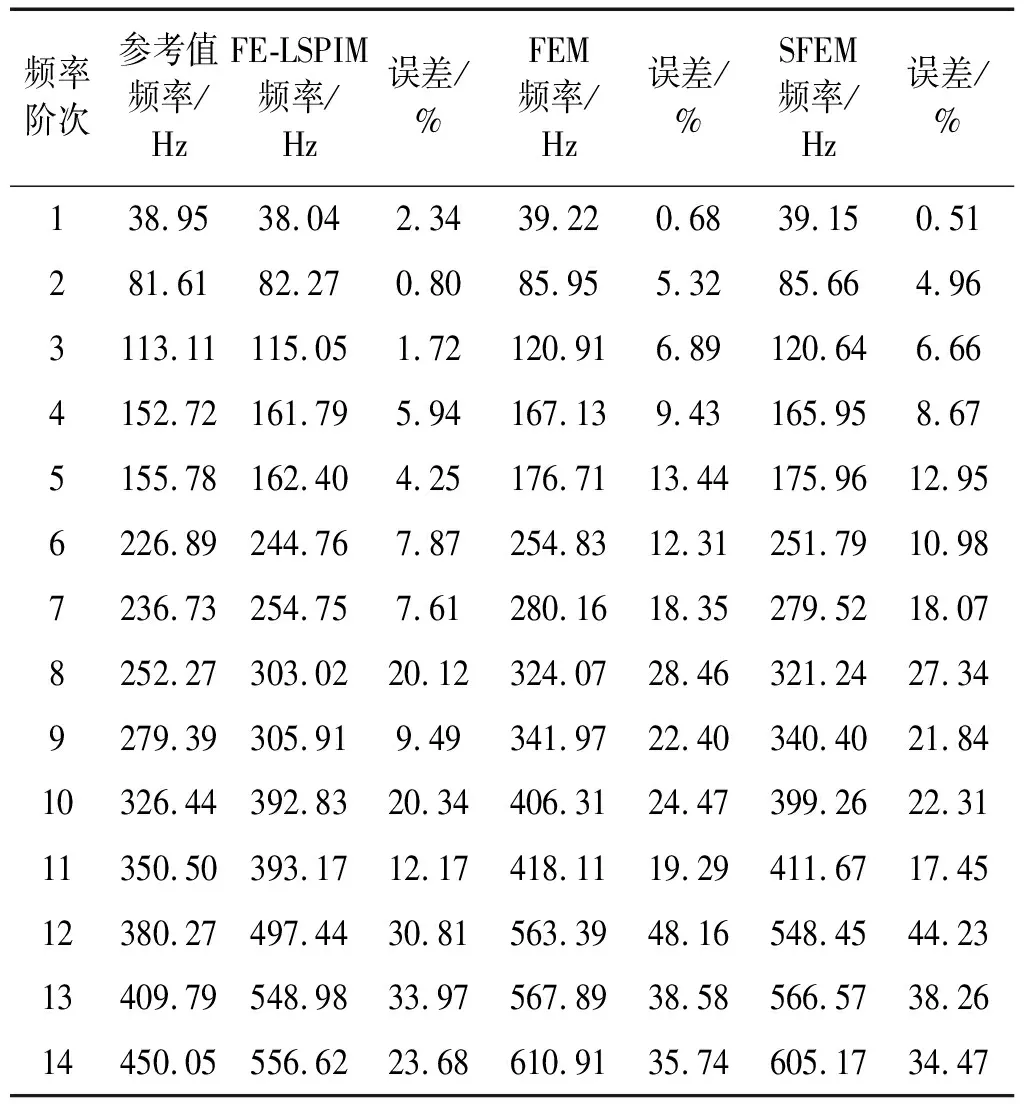
表2 应用FE-LSPIM、SFEM和FEM计算的板固有频率值
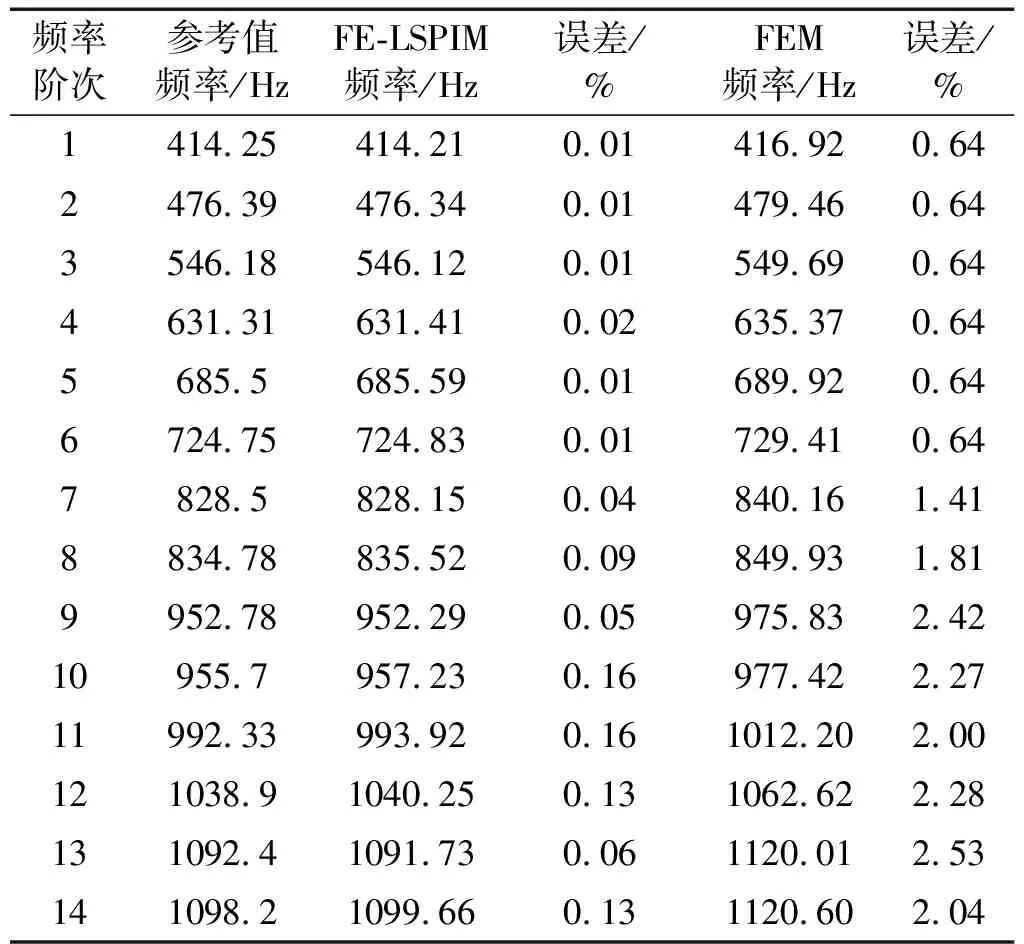
表3 应用FE-LSPIM、FEM计算的空腔固有频率值
表3所示为用FE-LSPIM计算得到声腔的前14阶非零固有频率值,耦合平面网格密度为8×8。表中同时给出了用FEM在相同网格模型下计算得到的声腔的前14阶非零固有频率值以及参考值,参考值由文献[1]得到。从表3中可以看出,随着特征频率阶次的增加,由FE-LSPIM和FEM所得结果的误差呈变大趋势,但FE-LSPIM所得结果明显比FEM所得结果更靠近参考值。
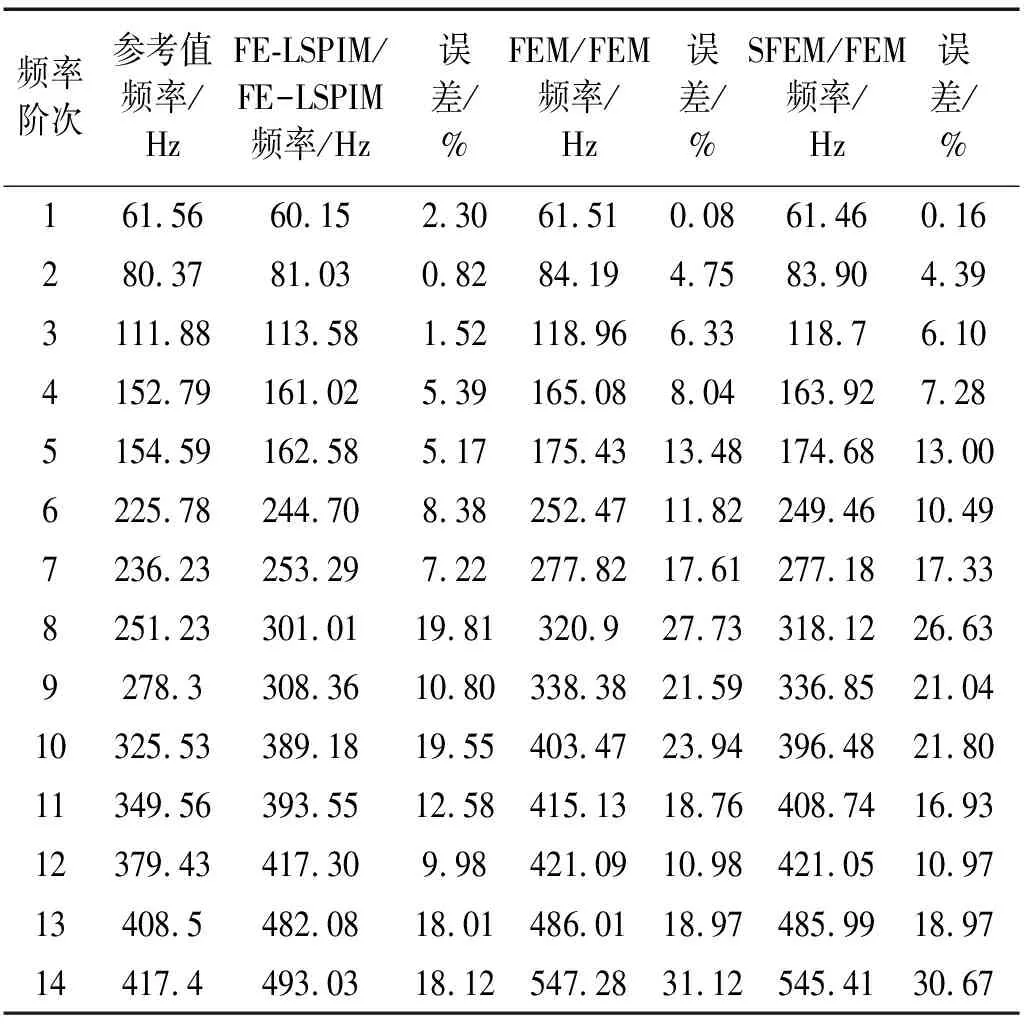
表4 应用FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM计算的耦合六面体声腔固有频率值
表4所示为用FE-LSPIM/FE-LSPIM计算得到耦合声腔的前14阶非零固有频率值,耦合平面网格密度为8×8。为了便于对比分析,表中同时给出了用SFEM/FEM、FEM/FEM在相同网格模型下计算得到的耦合声腔的前14阶非零固有频率值以及参考值,参考值由文献[1]得到。从表4中可以看出:
(1) 除了第一阶特征频率外,应用FE-LSPIM/FE-LSPIM计算得到耦合声腔的特征频率比应用SFEM/FEM、FEM/FEM计算所得结果更靠近参考值;
(2) 随着特征频率阶次的增加,FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM的计算结果更加远离参考值,计算误差整体呈变大趋势,但是在大多数情况下,FE-LSPIM/FE-LSPIM计算结果的误差明显小于SFEM/FEM和FEM/FEM计算结果的误差,相对能取得较高精度的结果。
为分析单元尺寸对FE-LSPIM/FE-LSPIM耦合声场计算结果的影响,将平板结构域和声场域耦合平面按不同网格密度划分成节点均匀分布的四边形网格,网格密度分别取:6×6、8×8、10×10、12×12、16×16,相应的结构域单元数和声域单元数如表1所示。为评价FE-LSPIM/FE-LSPIM的计算效果,同时给出FEM/FEM和SFEM/FEM的声压计算结果进行对比研究,参考值通过NASTRAN计算耦合平面网格密度为50×50的模型得到。表5和表6分别表示激振频率为150Hz及230Hz时应用FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM计算的域点1的声压值。
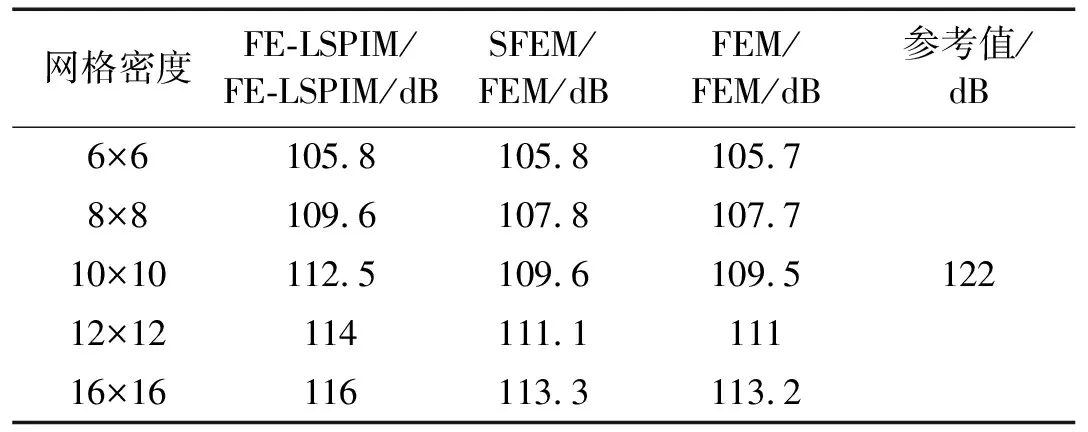
表5 激振频率为150 Hz时域点1声压
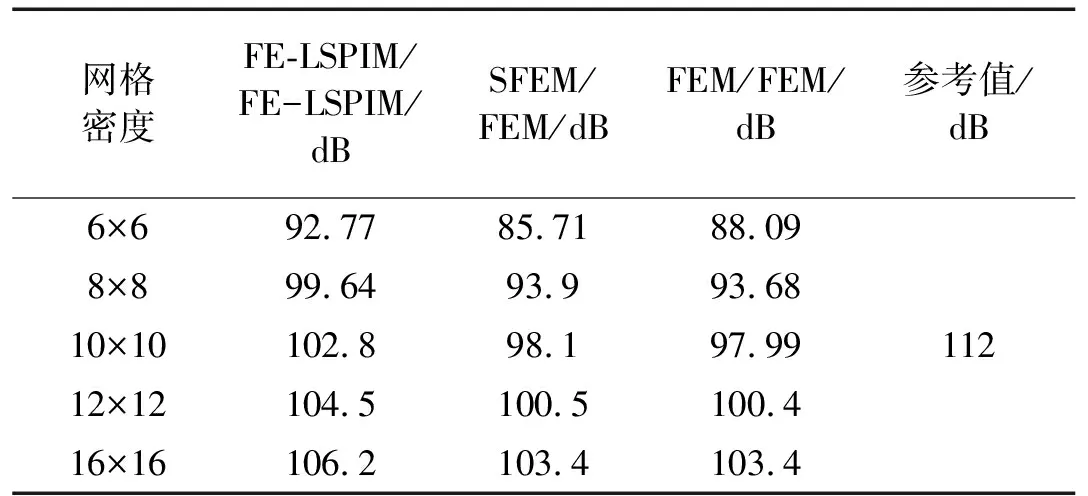
表6 激振频率为230 Hz时域点1声压
综合表5和表6可知:随着网格密度的增加(即单元尺寸的减少),FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM的计算结果都逼近参考结果,说明FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM都是收敛的,且FE-LSPIM/FE-LSPIM比SFEM/FEM和FEM/FEM收敛更快。
为了进一步评价FE-LSPIM/FE-LSPIM 分析结构-声场耦合问题的效果,本文计算了域点1和2的声压频率响应,计算频率范围为20~320 Hz,并给出了SFEM/ FEM和FEM/ FEM的计算结果作为对比,参考值通过FEM/ FEM计算耦合平面网格密度为16×16的模型得到。
图6和图7分别表示耦合平面网格密度为8×8时三种方法所计算的域点1和2的声压频率响应曲线。从图中可以看出:通过SFEM/FEM、FEM/FEM和FE-LSPIM/FE-LSPIM所得的声压频率响应曲线趋势与参考值相同,由于网格尺寸较大,计算结果均与参考值相差较大,但与SFEM/FEM和FEM/FEM相比,FE-LSPIM/FE-LSPIM的计算结果更接近参考值。这表明FE-LSPIM/FE-LSPIM比SFEM/ FEM和FEM/ FEM更精确,在同等粗糙的网格模型下计算结果更好。
图8为不同网格密度下用FE-LSPIM/FE-LSPIM、SFEM/FEM和FEM/FEM计算得到的域点1声压频率响应曲线,计算频率范围为20~320 Hz。FE-LSPIM/FE-LSPIM计算的耦合平面网格密度为8×8; SFEM/FEM和FEM/FEM计算的耦合平面网格密度分别取10×10和12×12。从图中可以看出,随着网格密度的增加,计算结果越准确,声压频率响应曲线整体向左移动靠近参考值。FE-LSPIM/FE-LSPIM在网格密度为8×8时的计算结果与SFEM/FEM和FEM/FEM在网格密度为12×12时的计算结果相接近,从而进一步说明了对粗糙网格模型,FE-LSPIM/FE-LSPIM比SFEM/ FEM和FEM/ FEM的计算精度更高。
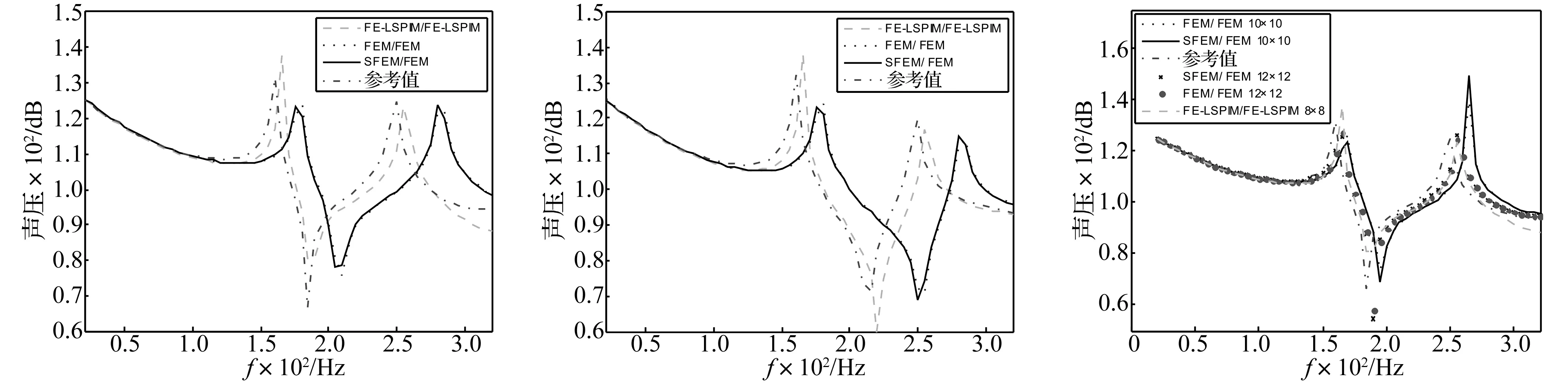
图6 域点1声压频率响应曲线
4 结 论
本文将FE-LSPIM推广用于Mindlin-Reissner板结构动力学和三维声场分析,提出用于板结构-声场耦合问题分析的FE-LSPIM/FE-LSPIM,推导了FE-LSPIM/FE-LSPIM分析板结构-声场耦合问题的计算公式。并以一六面体声场-结构耦合模型为研究对象进行分析,研究结果表明:FE-LSPIM/FE-LSPIM能很好地应用于板结构- 声场耦合分析中,其计算结果比SFEM/ FEM和FEM/ FEM收敛快,并且对单元网格尺寸要求比SFEM/ FEM和FEM/ FEM低,在计算较大网格尺寸模型时,能得到比SFEM/ FEM和FEM/ FEM更高的计算精度。因此,用FE-LSPIM/FE-LSPIM分析板结构-声场耦合问题可以减小计算规模、节省计算时间,具有良好的工程应用前景。
[1]He Z C, Liu G R, Zhong Z H, et al. A coupled edge-/face-based smoothed finite element method for structural-acoustic problems[J]. Applied Acoustics, 2010, 71: 955-964.
[2]He Z C, Liu G R, Zhong Z H, et al. Coupled analysis of 3D structural-acoustic problems using the edge-based smoothed finite element method/finite element method[J]. Finite Elements in Analysis and Design, 2010, 46: 1114-1121.
[3]Atalla N, Bernhard R J. Review of numerical solution for low-frequency structural-acoustic problems. Applied Acoustics, 1994(43):271-249.
[4]姚凌云,于德介,臧献国. 壳结构声场耦合分析的光滑有限元-有限元法[J]. 中国机械工程,2010,21(15):115-120.
YAO Ling-yun, YU De-jie, ZANG Xian-guo. Analysis of shell structural-acoustic coupling based on smoothed finite element and finite element method[J]. Chinese Mechanical Engineering, 2010,21(15):115-120.
[5]Melenk J M, Babu ska I. The partition of unity finite element method:basic theory and applications[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(1-4):289-314.
[6]Wenterodt C, Estorff O V. Dispersion analysis of the meshfree radial point interpolation method for the Helmholtz equation[J]. International Journal for Numerical Methods in Engineering, 2009,77:1670-1689.
[7]Rajendran S, Zhang B R. A “FE-Meshfree” QUAD4 Element for Free-vibration Analysis[J]. Computer Methods in Applied Mechanicals and Engineering, 2007, 197: 3595-3604.
[8]Rajendran S, Zhang B R. A “FE-Meshfree” QUAD4 Element Based on Partition of Unity[J]. Computer Methods in Applied Mechanicals and Engineering, 2007, 197: 128-147.
[9]姚凌云,于德介,臧献国. 声学数值计算的有限元-最小二乘点插值法[J]. 中国机械工程,2010,21(23):2816-2820.
YAO Ling-yun, YU De-jie, ZANG Xian-guo. A finite element-least square point interpolation method for acoustic numerical computation[J]. Chinese Mechanical Engineering, 2010,21(23):2816-2820.

