弹性波在对称准周期结构固/液声子晶体中的传播
肖绪洋,陈润平,夏继宏,席 锋
(1.重庆文理学院 电子电气工程学院,重庆 永川 402160; 2.重庆工商大学 计算机科学与信息工程学院,重庆 400067)
近年来,复合周期结构对经典波传播特性的调控引起了人们广泛的关注。声子晶体(Phononic crystal, PnC)是由弹性介质周期交替排列形成的复合材料[1-3]。弹性波在其中传输时,由于结构的周期性而形成声子带隙[4-7](Acoustic Band Gap, ABG),使频率落入声子带隙的弹性波被禁止传播。由于利用声子晶体的带隙能实现对弹性波的有效控制,故在声滤波、隔离噪声、减振,以及声学功能器件方面有着广泛的应用前景。
在对周期性结构的声子晶体研究中,已经发现声子晶体与光子晶体类似,存在声子局域态、超晶格折叠性、负折射等现象[8-10]。声波在周期结构声子晶体中的传输特性已有深入研究[11-13],对准周期结构声子晶体对弹性波的调控特性也有了新的认识[14-16]。现有对准周期结构声子晶体多基于弹性波在固体介质声子晶体的研究。通常研究固液介质声子晶体是将固体薄片或固体柱体浸入液体或空气中[17-18]。理想情况下,不考虑液体的黏滞效应时,只能传递弹性纵波。而某些介质常态时为固体,也只能传递弹性纵波[19],如聚乙烯,石英等,从这一角度考虑,也可当成“液”体介质对待。由固体介质和这类“液”体介质构成的声子晶体能脱离液体介质环境而独立存在,为其实际利用提供了方便。准周期结构是介于周期结构和无序结构之间的一种结构,相比于周期结构存在局域失谐。这种局域失谐结构产生的声子局域化现象与周期结构中由引入缺陷体产生的局域失谐有何区别,本文针对固“液”介质的Fibonacci序列的对称准周期结构声子晶体,研究弹性波在这种无序结构中的带隙特征和局域化现象以及入射角对声子晶体带隙的影响。
1 对称准周期结构声子晶体
一维Fibonacci序列准周期固液介质声子晶体由固体介质A和液体介质B构成。Fibonacci序列由迭代关系生成,设Fj={Fj-1,Fj-2} 当j≥2时,其中F0={A} 和F1={AB}。对称准周期结构表示为Sj=FjF’j,其中F’j为与Fj对应的对称结构。当j=5时的对称准周期结构声子晶体如图1所示,A为固体介质,B为液体介质,其厚度分别为da,db。
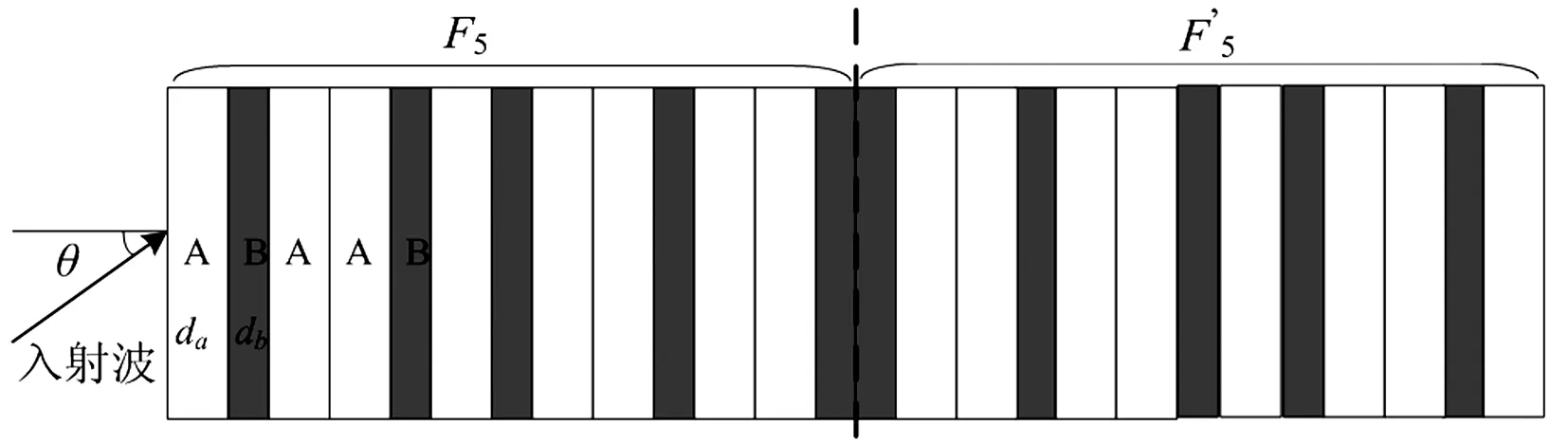
图1 对称准周期结构声子晶体
在不考虑液体介质的横向粘滞效应情况下,液体介质中不能传输横波,只能传输纵波。在相邻固液介质的界面上,根据位移和应力在界面的连续条件,得到在相邻界面上前行波和后行波的振幅关系为:
(1)
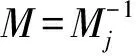
(2)
式中;
和
(3)
式中:θ为声波在端面的入射角,θjT和θjL分别为横波和纵波在固体介质面上的入射角,θj+1为声波在液体界面上的入射角,均由Snell定律确定;λ和μ分别为固体介质的拉梅常数,下标L表示纵波,T表示横波。
波通过厚度为dj的介质后,仅有相位发生变化,相应的传输矩阵为:
(4)
在一个周期内的传输矩阵可写为:
(5)
进而可得到整个对称准周期声子晶体的传输矩阵,并可进一步求得透射率和反射率。
2 数值结果和讨论
固体介质A和液体介质B分别为铝和聚乙烯,相应的物理参数为:ρa=2 700 kg/m3,cLa=6 350 m/s,cTa=3 080 m/s,ρb=920 kg/ m3,cb=2 000 m/s,介质厚度da=cLa/4f0,db=cb/4f0,f0(=10 kHz)为入射弹性波的中心频率。环境介质为水,ρ0=1 000 kg/ m3,c0=1 480 m/s。利用传输矩阵法进行数值计算,并分析弹性波在不同准周期序列的对称结构声子晶体中的传输特性。
2.1 弹性波正入射
中心频率为f0弹性纵波正入射,序列分别为S4、S5、S6和S7的准周期对称结构声子晶体的透射特性如图2(a)、(b)、(c)和(d)所示。从图中看出,在中心频率f0处出现了局域谐振模,频率半高宽仅为几Hz;其带隙比由A和B构成的周期声子晶体带隙要宽[19],且随着序列的增加,带隙略有展宽。实际上,在透射谱中,中心频率奇数倍处都将出现谐振模,这与周期结构中心缺陷的情况相同[21]。为了方便,我们仅讨论一级声子带隙。从图2(a)、(b)和(c)的插入图发现,除了中心频率处的局域谐振,还在中心频率两侧对称的出现两条次级局域谐振模,其频率半高宽较中心局域谐振模频率半高宽窄。序列越大,局域谐振越强,因而品质因子(中心频率/频率半高宽)越高。
由于低序列的准周期声子晶体,主要表现出结构的非周期性,相当于在周期结构中加入多个缺陷层。因此,弹性波从准周期结构声子晶体透射后将产生局域谐振模。当准周期序列增大时,准周期声子晶体的无序性降低,而有序性增强,将主要表现出周期结构的特性。在所讨论的对称准周期结构声子晶体中,在对称面两侧(对称中心处),奇数序列为介质B,偶数序列为介质A。由此可以把这两层介质看做缺陷体,又因为处于结构中心处,因而在透射谱的带隙中心应出现局域谐振模,这与局域理论完全相符。
图2(d)所示为弹性波在S7序列中的透射谱。在该透射谱中,只在中心频率处出现一条局域谐振模,但其顶部不再平坦,变为锯齿状。由于结构层数增多使局域谐振增强,同时对局域声子的选频作用也增强,使次级局域谐振模向中心频率靠近而合并,次级局域谐振模消失。
在图2(b)、(c)和(d)中,在0.3f0和1.7f0附近出现带边谐振,且随着序列的增加,带边的谐振增强。而图2(a)中,由于S4序列(ABAABABAABABAABA)相当于在周期结构中引入三个缺陷层,其透射谱中出现三个局域谐振模,带边没有局域谐振。另外,从图中对比还发现,序列越高,中心谐振模的带边越陡。这是因为序列增加时,系统结构的层数增加更快,谐振越强,从而使声子局域频率的带宽变窄。
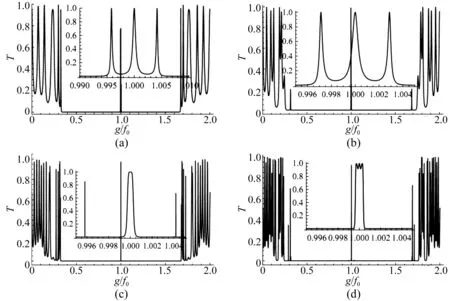
图2 正入射时不同对称序列准周期声子晶体的透射谱
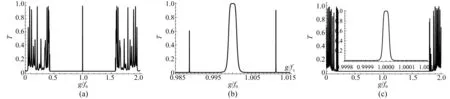
图3 不同介质时S6序列的透射谱
弹性波在由不同介质构成的S6序列中的透射如图3所示。图3(a)和(b)为液体介质B为黏合剂(ρb=1 738 kg/ m3,cb=2 240 m/s),固体介质A为铝时的弹性波透射谱。与图2(c)相比,声子带隙变窄,带边局域谐振减弱。图3(c)为液体介质B为聚乙烯,固体介质A为钢(ρa=7 800 kg/m3,cLa=5 850 m/s,cTa=3 230 m/s)时弹性波的透射谱。其带隙增宽,带边局域谐振更强。透射谱变化的主要原因在于介质的波阻抗(Z=ρcL)不同。铝和聚乙烯的波阻抗比为ZA/ZB=9.32,铝和黏合剂的波阻抗之比为ZA/ZB=4.40,钢和聚乙烯的波阻抗之比为ZA/ZB=24.80。固液介质的波阻抗越大,带隙越宽,局域谐振场强。当固体介质为钢时,由于介质的波阻抗相差太大,只有中心处的局域谐振能透射,抑制了次级谐振。
2.2 弹性波斜入射
为清晰认识弹性纵波在该对称准周期固液介质声子晶体中的传输特性,需要研究弹性纵波斜入射时纵波的透射谱。由Snell定律,固液介质界面上的临界角为θc=arcsin(cb/cLa)=18.4°。在固液界面上弹性波的入射角大于时由于发生全反射而不能在结构中传输。当弹性纵波以5°斜入射S4、S5、S6和S7的对称准周期结构声子晶体时,相应的透射谱如图4(a)、(b)、(c)和(d)所示。从图中看出,斜入射时,一级带隙略微展宽,并向高频区移动,这一特点与周期结构声子晶体相同[16]。同时在频率2.00f0~2.10f0内出现次级带隙。
另外,一级带隙的带间谐振和带边谐振以及级次带隙的带间谐振随着序列的增加显著增强。从图中看出,固液声子晶体对弹性波入射角很敏感,弹性波以较小的角度入射,就能使声子带隙发生很大的变化。弹性波斜入射时,透射谱发生频移,使原来在中心频率处的局域谐振模也向高频区移动,出现在1.07f0附近。当弹性波以15°斜入射S7序列的透射如图4(e)所示。此时只有低频弹性波透射,其频率上限约为0.54f0,频率大于此值的弹性波在端面被全反射。从插入图中还可以算出,在0.26f0~0.31f0间出现一个低频带隙。次级带隙产生的原因在于,入射的弹性纵波在固体介质中将有一部分转换为横波,而这一部分横波是不能在液体介质中传播的。
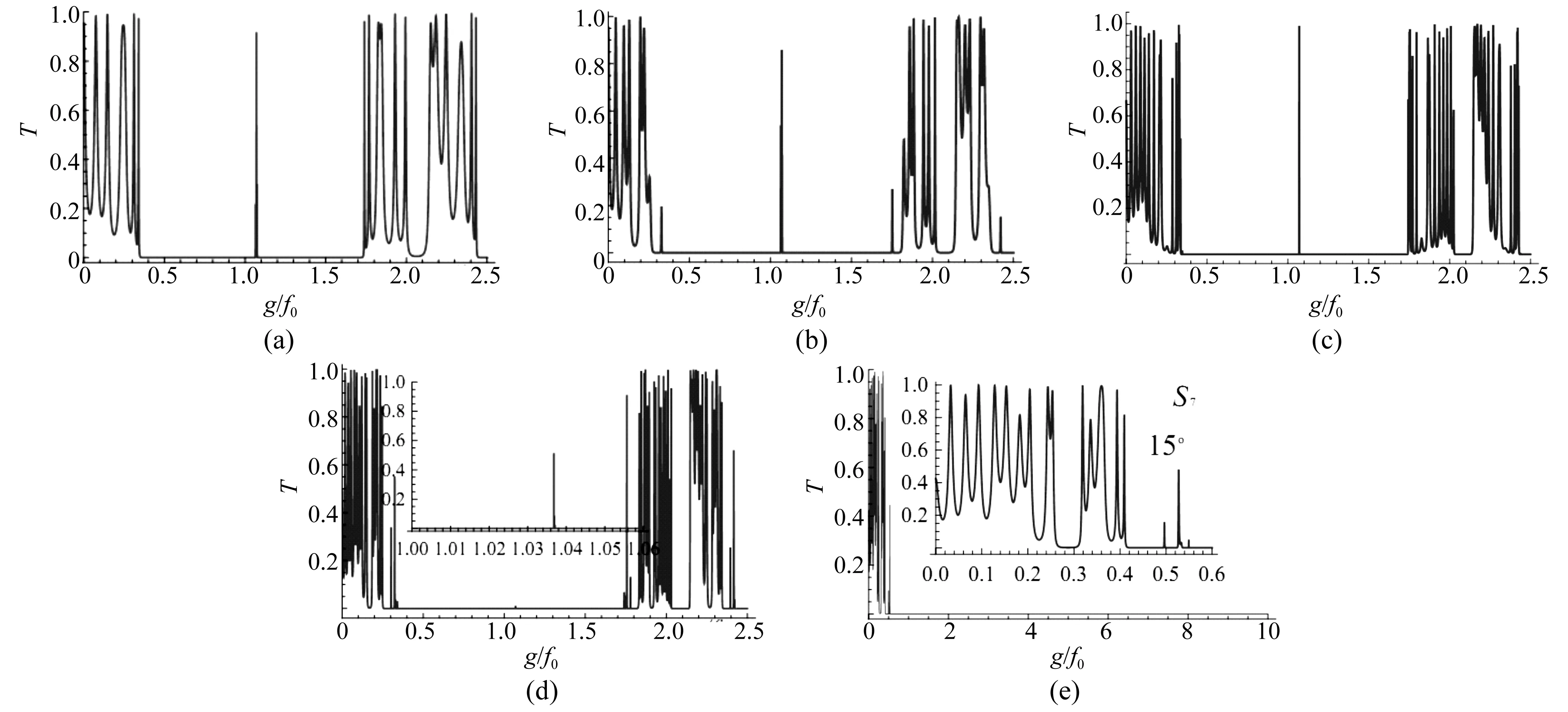
图4 斜入射时不同对称序列准周期声子晶体的透射
3 结 论
本文基于Fibonacci准周期序列,提出了一维固液介质声子晶体的对称准周期结构。利用传输矩阵法,研究了弹性纵波在其中的透射特性。数值研究的结果表明,弹性波正入射时,该对称准周期固液声子晶体的带隙中,由于结构的失谐,在中心频率附近出现局域谐振模,其频率带宽仅为几Hz,因此,利用该准周期结构声子晶体获得的局域谐振模,比通过引入缺陷结构得到的谐振模有更高的品质因子。根据这一特点,利用不同的对称准周期序列,可实现超窄带的多通道滤波。当弹性波以较小的角度斜入射时,声子带隙以及带隙中的局域谐振模都略微向高频方向移动,同时出现次级声子带隙。
利用弹性波在对称准周期结构声子晶体中的局域失谐,得到品质因子很高的局域谐振模,以实现超窄带声子滤波,这对设计和制备声波器件具有重要意义。
[1]Kushwaha M S. Acoustic band structure of periodic elastic composites[J]. Phys. Rev. Lett. 1993, 71(13):2022-2025.
[2]Jesen J S, Phononic band gaps and vibrations in one-and two-dimensional mass-spring structures[J]. Journal of Sound and Vibration, 2003, 266(5):1053-1078.
[3]Wang Gang, Yu Dian-long, Wen Ji-hong. One-dimensional phononic crystals with locally resonant structures[J]. Physics Letters A, 2004, 327(5-6):512-521.
[4]Sigalas M M, Soukoulis C M. Elastic-wave propagation through disordered and/ or absorptice layered systems[J]. Phys. Rev. B, 1995,51(5): 2780-2789.
[5]Liu Z Y, Zhang X X, Mao Y W, et al. Locally resonant sonic materials[J]. Science, 2000, 289: 1734-1736.
[6]Wang G, Wen X S, Wen J H, et al. Two-dimensional locally resonant phononic crystals with binary structure[J]. Phys. Rev. Lett. 2004, 93(15):154302.
[7]舒海生,刘少刚,王威远,等.集中质量边界条件下声子晶体杆的纵向振动传递特性研究[J]. 振动与冲击,2012,31(19):113-117.
SHU Hai-sheng, LIU Shao-gang,WANG Wei-yuan, et al. Transmission characteristic of longitudinal vibration of a phononic crystal rod with concentrated mass boundary condition[J]. Journal of Vibration and Shock,2012,31(19):113-117.
[8]温激鸿,王刚,刘耀宗,等,基于集中质量法的一维声子晶体弹性波带隙计算[J].物理学报,2004,53(10),3384-3388.
WEN Ji-hong, WANG gang, LIU Yao-zhong, et al. Lumped-mass method on calculation of elastic band gaps of one-dimensional phononic crystals[J], Acta Physica Sinica, 2004,53(10),3384-3388.
[9]吴福根,刘有延,二维周期性复合介质中声波带隙结构及其缺陷态[J], 物理学报,2002,51(7),1434-1438.
WU Fu-gen, LIU You-yan. Acoustic band gaps and defect states in two-dimensional composite materials[J]. Acta Physica Sinica, 2002, 51(7):1434-1438.
[10]Peng Pai, Qiu Chun-yin, Ding Yi-qun, et al, Acoustic tunneling through artificial structures: From phononic crystals to acoustic metamaterials[J].Solid State Communications, 2011, 151(5): 400-403.
[11]Hou Zhilin, Badreddine M A, Transmission property of the one-dimensional phononic crystal thin plate by the eigenmode matching theory[J]. Journal of Phys. D: Appl. Phys. 2008, 41(9): 095103.
[12]Khelif A, Djafari-Rouhani B, Vasseur J O, et al, Transmission and dispersion relations of perfect and defect-containing waveguide structures in phononic band gap materials[J]. Phys. Rev. B, 2003,68(2):024302.
[13]宿星亮, 高原文. 含有功能梯度材料的一维声子晶体弹性波带隙研究[J]. 固体力学学报,2012,33(1):75-80.
SU Xing-liang, GAO Yuan-wen. Research on band gap of one-dimensional phononic crystals with functionally graded materials[J]. Chinese Journal of solid mechanics, 2012, 33(1): 75-79.
[14]曹永军, 董纯红, 周培勤.一维准周期结构声子晶体透射性质的研究[J]. 物理学报,2006,55(12):6470-6475.
CAO Yong-jun, DONG Chun-hong, ZHOU Pei-qin. Transmission properties of one-dimensional qusi-periodical phononic crystal[J]. Acta Physica Sinica, 2006, 55(12): 6470-6474.
[15]杨立峰, 王亚非, 周鹰. 一维压电Fibonacci类准周期声子晶体的传输特性[J]. 物理学报,2012,61(10):107702-6.
YANG Li-feng, WANG Ya-fei, ZHOU Ying. The transmission properties in one-dimensional piezoelectric Fibonacci-class quasi-periodical phononic crystals[J]. Acta Physica Sinica, 2012, 61(10):107702-6.
[16]Wang Gang, Wen Ji-hong, Wen Xi-sen, Quasi-one-dimensional phononic crystals studied using the improved lumped-mass method: Application to locally resonant beams with flexural wave band gap[J]. Phys. Rev. B, 2005, 71(10):104302-5.
[17]刘启能. 固流结构声子晶体中弹性波能带的色散研究[J]. 人工晶体学报,2009,38(1):107-112.
LIU Qi-neng. Dispersive study on the photonic bandgap of solid and fluid phononic crystal[J]. Journal of Synthetic Crystals, 2009, 38(1):107-112.
[18]Romero-Garcia V, Sanchez-Perez J V, Castineira-lbanez S, et al, Evidences of evanescent Bloch waves in phononic crystals[J]. Appl. Phys. Lett. 96(12), 2010, 124102.
[19]Rose J L. 固体中的超声波[M]. 何存富, 吴斌, 王秀彥译. 北京: 科学出版社, 2004.
[20]刘启能. 一维声子晶体的传输特性[J]. 人工晶体学报,2008,37(1):179-182.
LIU Qi-neng, Transfer characteristic of one-dimensional phononic crystal[J]. Journal of Synthetic Crystals, 2008, 37(1):179-182.
[21]朱 敏,方云团,沈廷根. 一维声子晶体的缺陷态的研究[J]. 人工晶体学报,2005,34(3):536-541.
ZHU Min, FANG Yun-tuang, SHEN Ting-gen, Study on one-dimensional phononic crystal with defects[J]. Journal of Synthetic Crystals, 2005, 34(3):536-541.

