基于广义DF法的参数可调二阶滑模抖振特性分析
申 宇,仇原鹰
(1.西南大学 计算机与信息科学学院,重庆 400715;2.西安电子科技大学 电子装备结构设计教育部重点实验室,西安 710071)
非线性系统中普遍存在自激振荡现象[1]。而该现象在滑模控制中尤为引人关注,即滑模控制的抖振。抖振对滑模控制系统的影响主要表现为:较大的抖振幅度将降低控制精度;抖振频率与系统谐振频率相近时易引发系统共振;过快的抖振频率可能超出控制器允许的最大切换速率。如文献[2]中,Bang-Bang控制器引入的抖振频率就必须小于磁流变阻尼器允许的电压切换速率,而该文献并未提出如何调节抖振频率。因此,如何估算和调节系统的抖振特性(即抖振幅度An和抖振角频率ωn)成为滑模控制的重要研究问题。
趋近率滑模[3]是滑模控制的典型代表,学者们通常在时域上研究如何抑制切换控制所引入的抖振,利用全部状态变量设计滑模面参数,再设计“准滑动模态”或“低通滤波器”[4]来削弱抖振。由于时域分析法的局限性,学者们一般通过仿真实验曲线来评估对抖振的抑制效果,但这样的设计思路存在以下问题:① 在工程应用中很难测量全部状态变量;② 一般采取定性的方法分析抖振的抑制效果,无法准确计算抖振特性;③ 很难找出抖振特性与控制系统参数之间的对应关系,因而无法灵活调节抖振特性。
由于滑模切换函数的非连续性和多样性,仅采用时域法分析滑模抖振特性已力不从心。因此,有学者借助频域经典描述函数(DF)法来分析该问题。Oliveira等[5]利用经典DF法为不确定系统设计的滑模控制器,通过调整G(s)与-1/N(A)幅相频率特性曲线相交位置实现抖振特性的定量调节,并提高了系统鲁棒性;Huang等[6]运用经典DF法分析了滑模控制器的稳定性和极限环,并研究各种切换函数对抖振特性的影响;Boiko近十年时间,在经典DF法基础上提出了滞环控制器[7]、输出反馈缠绕控制器[8]、二阶滑模控制器[9-10]的抖振特性计算和调节方法。但是基于经典DF法的滑模抖振研究仍然存在一些问题:只能分析滑模面的抖振特性而无法分析系统各状态变量的抖振特性;只能分析与振幅A相关的简单描述函数N(A),而不能分析与振幅A和角频率ω相关的复杂描述函数N(A,ω)。
为更完善地研究滑模控制的抖振特性,本文将以一类参数可调2-SMC为研究对象,首先利用经典DF法,找到系统输出量y(t)的抖振特性随控制参数变化的规律;接着针对复杂非线性环节提出广义DF法,以估算抖振特性并分析抖振稳定性;最后利用广义DF法估算系统状态变量的抖振特性。
1 控制系统设计
考虑如图1所示的自治反馈控制系统,其中被控对象G(s)=G1(s)G2(s),且G1(s)与G2(s)的零极点均位于左半平面或虚轴上;x1,x2为待分析的状态变量;u为被控系统输入量;y为被控系统输出量且y=x1。
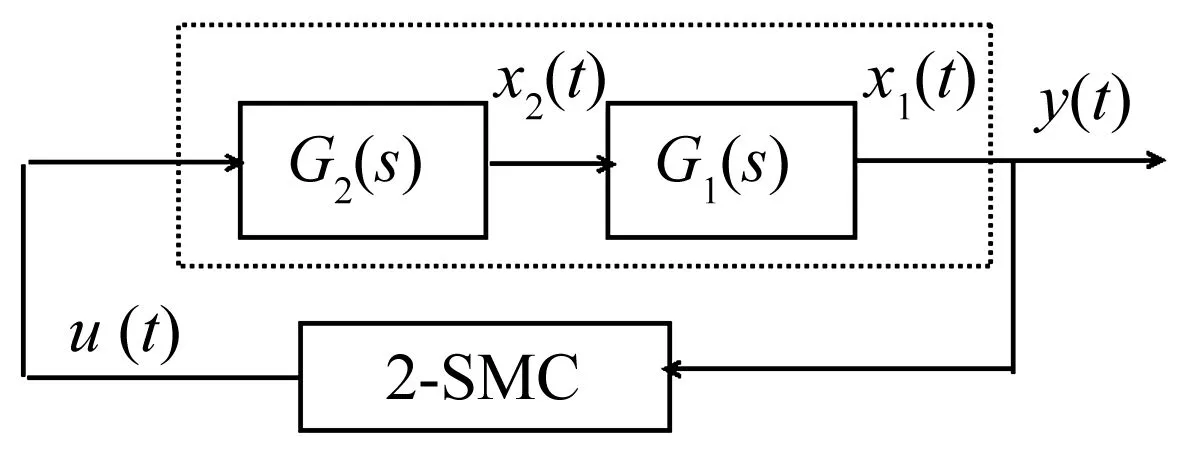
图1 二阶滑模控制系统
图1中2-SMC为可调二阶滑模控制器[11],其输出控制量表示为
u(t)=-α(t)Msign(σ(t))
(1a)
(1b)
σ(t)=y(t)-βyM(t)
(1c)
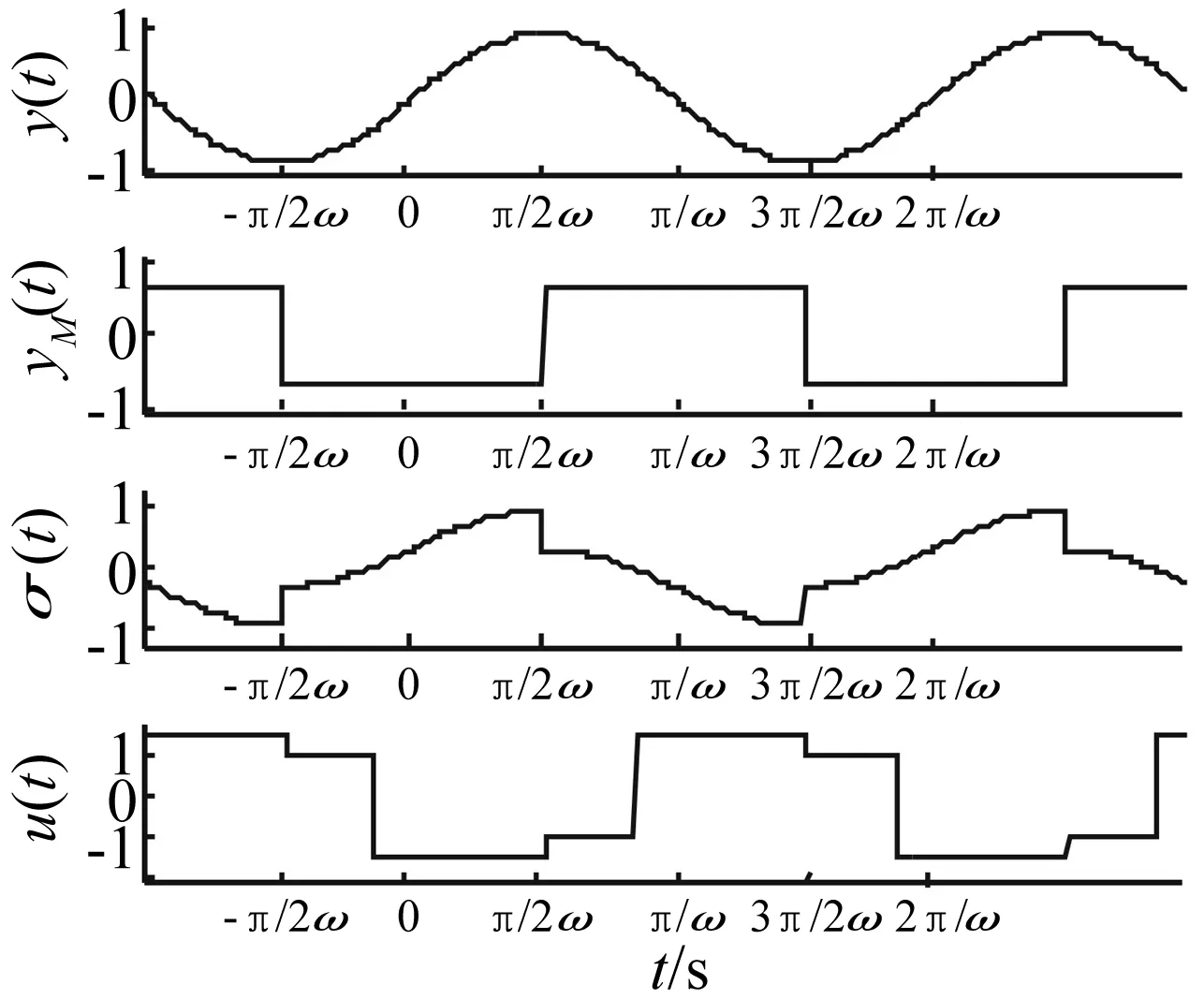
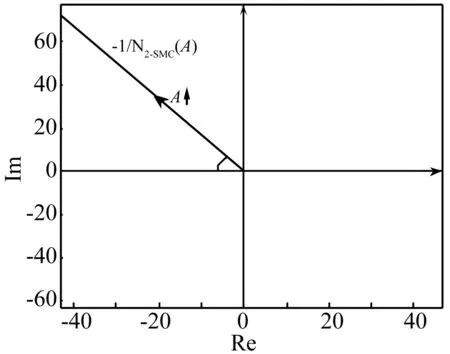
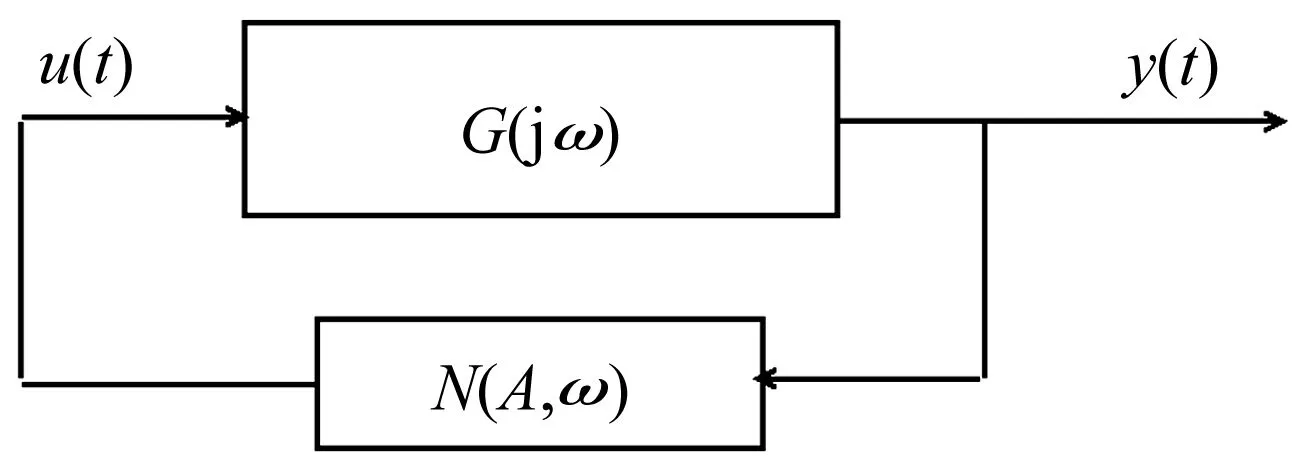
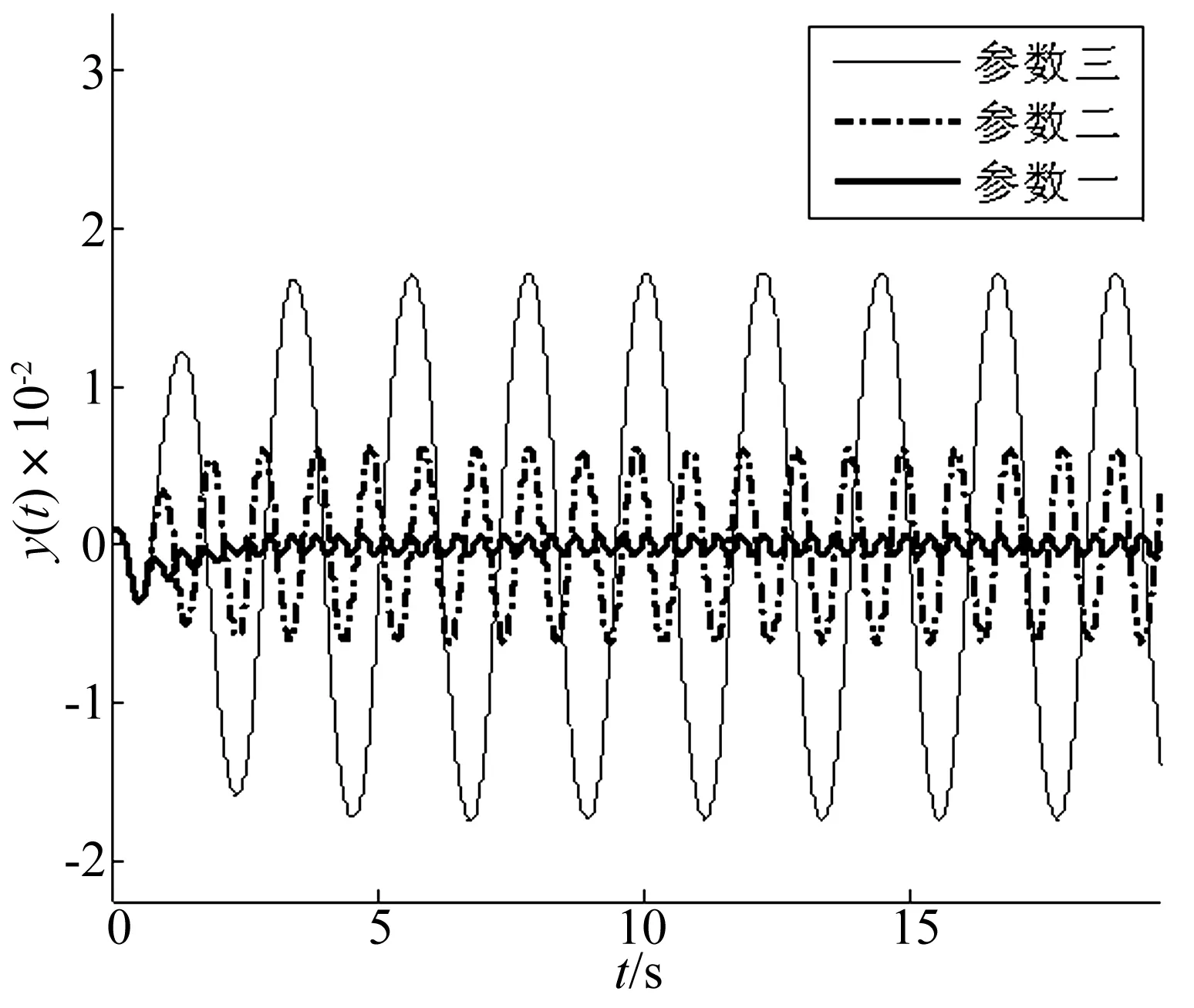
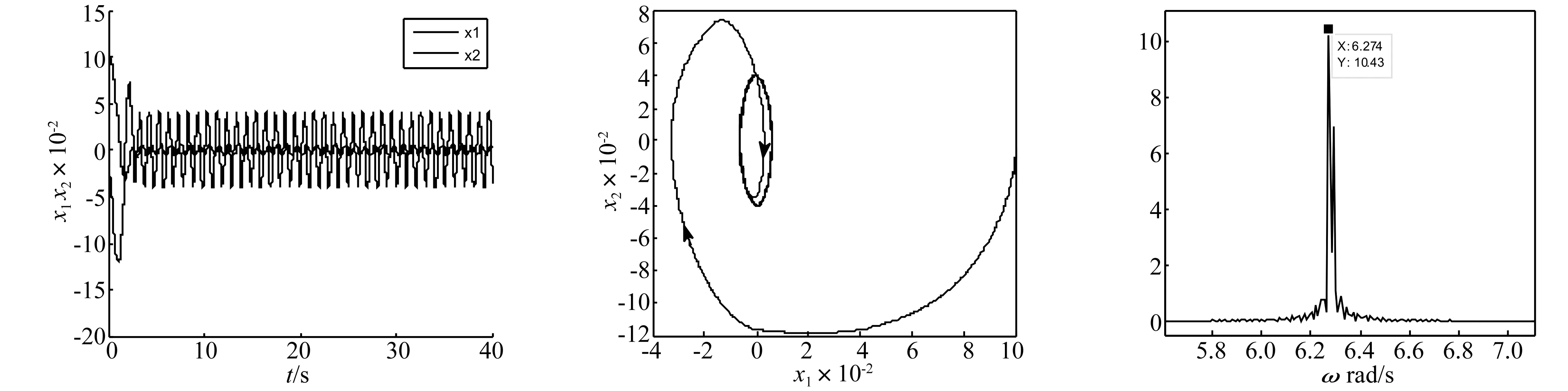
式中:M为控制器增益;α*>0;β∈(0,1];yM(t)定义为输出量y(t)的最新极值,并设定yM(0)=0。yM(t)可理解为:若存在多个时刻td1 则 本小节将利用经典描述函数法,分析控制系统的稳定性和输出量抖振特性。首先计算2-SMC对应的负倒描述函数-1/N1(A),在2-SMC的输入端施加正弦信号Asin(ωt),并依次得到对应的yM(t)、σ(t)和控制器输出u(t)波形,如图2所示。 图2 正弦激励输出波形 对输出u(t)谐波线性化处理,得到其基波分量A1和B1: (2a) (2b) 可以看到当参数α*和β确定后,A1、B1与施加信号的频率无关,即为频率无关基波分量。因此,也称其对应的非线性环节为简单非线性环节。利用基波分量可得到2-SMC的负倒描述函数-1/N1(A): (3) 将-1/N1(A)绘制于复平面,如图3所示。 图3 -1/N1(A)曲线 -1/N1(A)曲线是始于原点的直线,并随着参数A的增大而远离原点,与实轴的夹角φ可表示为: (4) 结合图3和式(4)可以看到,若(α*-1)+β(α*+1)>0,则-1/N1(A)曲线位于第二象限;若(α*-1)+β(α*+1)<0,则-1/N1(A)曲线位于第三象限;若(α*-1)+β(α*+1)=0,则-1/N1(A)曲线为实轴负半轴。因此通过调整参数α*和β,控制器2-SMC的负倒描述函数曲线可在-90°~-270°间旋转,从而改变G(jω)与-1/N1(A)的交点。利用经典DF法分析闭环系统的稳定性和抖振特性,可使控制系统输出量y(t)的抖振特性满足期望性能。 在上一节利用经典DF法分析了简单非线性环节所引入的抖振特性。然而也存在一些较复杂的非线性环节(如图4所示),其描述函数N(A,ω)与施加信号的频率有关,因而不再适用于经典DF法。在本节将针对N(A,ω)提出一种广义DF法,以求取抖振的稳定性和抖振特性。 图4 复杂非线性系统框图 将图4所示闭环系统的幅相频率特性表示为1/[1+G(jω)N(A,ω)],在奈氏稳定判据的基础上,提出基于数值计算的广义DF法稳定判据: 步骤1:确定角频率分析范围0<ω≤ωup,ωup为分析的角频率上限; 步骤2:判断在角频率分析范围内是否存在抖振特性(An,ωn),使得Im[G(jωn)N(An,ωn)]=0与Re[G(jωn)N(An,ωn)]=-1同时成立(可能存在多个抖振特性); 步骤3: 若An,ωn满足式(5)和式(6),则(An,ωn)为稳定的抖振点; (5) (6) 步骤4: 若An,ωn满足式(7)和式(8),则(An,ωn)为稳定的抖振点; (7) (8) 步骤5: 否则(An,ωn)为非稳定的抖振点。 判断抖振(An,ωn)的稳定性,关键是分析G(jω)N(A,ω)特性曲线与点(-1, j0)的位置关系。依据奈氏稳定判据,若当A>An,G(jω)N(A,ω)不包围(-1, j0);当A 图5(a) 稳定抖振的幅相频率特性 图5(b) 非稳定抖振的幅相频率特性 接下来利用图5解释步骤3~步骤5:图5(a)中,当A=1.6时,G(jω)N(A,ω)特性曲线与负实轴交于(-1, j0)点且斜率为正,满足式(5),随着A的增大(减小),特性曲线与负实轴交点向右(左)移动,满足式(6),依据奈氏稳定判据,其对应的抖振是稳定的;图5(b)中,当A=0.033时,特性曲线与负实轴交于(-1, j0)点且斜率为负,满足式(7),随着A的增大(减小),特性曲线与负实轴交点向右(左)移动,不满足式(8),依据奈氏稳定判据,其对应的抖振是不稳定的。 在实际应用中,特性曲线以正斜率穿越(-1, j0)的情况较多,而以负斜率穿越的情况少见。 在第2节中只分析了系统输出量y(t)的抖振特性,而在工程应用中同样十分关注其它状态变量的抖振特性。在本节将利用广义DF法分析图1中状态变量x2(t)的抖振特性。 图6 重组后的系统框图 在图1基础上重新划分线性和非线性环节,得到图6所示框图。可直观地看到非线性环节N2包含滑模控制器和G1(s),因此,N2一定与施加信号的角频率ω相关,只能利用广义DF法来分析x2(t)的抖振特性。 接下来将计算N2的描述函数,在N2的输入端施加信号Asin(ωt),可得到x1(t)、yM(t)、σ(t)和u(t)的波形。由频率法可知,x1(t)与x2(t)应同为正弦信号而相位和幅度受G1(s)决定,因此可将x1(t)表示为式(9): x1(t)=A0(ω)Asin(ωt+θ0(ω)) (9) 其中A0(ω)和θ0(ω)为G1(s)的幅频特性和相频特性。于是计算N2的基波分量: (10a) (10b) 从而得到N2的描述函数N2(A,ω)=B1/A+jA1/A。最后借助广义DF法,可求出状态变量x2(t)的抖振特性。 设计如图1所示控制系统,其中被控对象为G1(s)=1/(s+3),G2(s)=1/((s+1)(s+2)),二阶滑模控制器为式(1)所示控制器。本节将进行两项实验:实验一选取多组控制器参数α*和β,将y(t)的抖振仿真结果与经典DF法估算结果比较,以验证控制参数α*、β与抖振特性的关系;实验二将以状态变量x2(t)为研究对象,通过计算复杂描述函数,运用广义DF法估算其抖振特性,同时与仿真结果对比。 为分析参数α*和β对控制系统抖振特性的影响,设置三组控制器参数如表1所示。利用经典DF法估算输出量y(t)的抖振特性并与Matlab仿真实验结果对比。首先绘制被控对象G(s)幅相频率特性曲线和控制器负倒描述函数-1/N1(A)曲线,如图7所示。从图7可看到2-SMC的负倒描述函数曲线-1/N1(A)随着参数α*和β的减小而逆时针旋转,并从第二象限旋转到第三象限。随着-1/N1(A)逆时针方向旋转,-1/N1(A)与G(s)的交点向角频率减小方向运动,因而y(t)的抖振角频率减小、抖振幅度增大。图8为三组控制参数对应的y(t)仿真响应曲线,并测量了各自的抖振特性。表1列出了三组控制器参数对应的抖振特性的估算和仿真结果,可看到y(t)抖振角频率的理论估算与仿真实验结果较吻合,而抖振幅度的估算值稍小于仿真实验结果,这可能是由于DF法只分析基波分量,而造成了一定误差。 图7 描述函数分析 图8 三组参数对应的y(t)响应曲线 因此得到N2的描述函数N2(A,ω)=B1/A+jA1/A,以及G2(jω)N2(A,ω)的表达式。当选定控制器参数α*=1.5,β=0.5,M=1时,利用广义DF法并经过一系列代数运算和求导计算,可求得An=0.031,ωn=6.5 rad/s,且G2(jωn)N2(An,ωn)满足广义DF法步骤3的抖振稳定条件。 在仿真实验中,利用Matlab仿真了图6所示的控制系统,得到了x1(t)、x2(t)的仿真响应曲线如图9(a)所示。绘制了以x1(t)-x2(t)为相平面的相轨迹如图9(b)所示,可看到系统从初始状态x1(0)=0.1,x2(0)=0出发,围绕平衡点旋转并趋近,最终稳定于一极限环运动。对x2(t)傅里叶分析,截取1 000点数据进行频谱分析如图10所示。由于x2(t)的响应为近似正弦曲线,因此含有多个频谱分量。从图10中可看到频谱中有两个峰值,分别对应角频率6.274 rad/s和6.294 rad/s。从图9、图10可看到,仿真实验所得x2(t)的抖振特性为An≈0.040,ωn≈6.3 rad/s。x2(t)抖振特性的广义DF法计算结果与仿真实验基本吻合,特别是角频率的估计精度较高(误差小于6%),印证了广义DF法的正确性。 图9(a) x1(t)、x2(t)响应曲线 利用经典和广义DF法,研究了2-SMC可调参数影响系统抖振特性的机理,推导了系统输出量和状态变量抖振特性的估算方法,得到了系统抖振特性的调节方法。提出了广义DF法以分析复杂非线性环节的抖振特性,给出了抖振的稳定条件,并利用广义DF法估算了控制系统状态变量的抖振特性。实验数据对比表明,经典和广义DF法对抖振角频率的估算精度较高。该方法可指导滑模控制系统的设计,从而抑制系统抖振幅度、调节抖振频率、避免系统共振。 [1]Billings S A, Tsang K M. Spectral analysis for non-linear systems, part Ι: parametric non-linear spectral analysis[J]. Mechanical Systems and Signal Processing, 1989, 3(4): 319-339. [2]禹见达, 陈政清, 王修勇等. 改进的 Bang-Bang控制算法的理论与试验研究[J]. 振动与冲击, 2010, 29(2): 60-63. YU Jian-da, CHEN Zheng-qing, WANG Xiu-yong, et al. Theoretical and experimental study on an improved Bang-Bang control algorithm[J]. Journal of Vibration and Shock, 2010, 29(2): 60-63. [3]Gao W B, Wang Y F, Homaifa A. Discrete-time variable structure control systems[J]. IEEE Transactions on Industrial Electronics, 1995, 42(2): 117-122. [4]Lee H, Utkin V I. Chattering suppression methods in sliding mode control systems[J]. Annual Reviews in Control, 2007, 31(2):179-188. [5]Oliveira N M F, Kienitz K H, Misawa E A. A describing function approach to the design of robust limit-cycle controllers[J]. Nonlinear Dynamics, 2012, 67(1): 357-363. [6]Huang Y J, Wang Y J. Steady-state analysis for a class of sliding mode controlled systems using describing function method[J]. Nonlinear Dynamics, 2002, 30(3): 223-241. [7]Boiko I. Analysis of modes of oscillations in a relay feedback system[C]. Proceeding of the 2004 American Control Conference Boston, Massachusetts, June, 2004: 1253-1258. [8]Boiko I. Oscillations and transfer properties of relay feedback systems with time-delay linear plants[J]. Automatica, 2009, 45(12): 2897-2902. [9]Boiko I, Castellanos I, Fridman L. Analysis of response of second-order sliding mode control systems to exteral inputs[C]. Proceedings of the 2006 International Workshop on Variable Structure Systems Alghero, Italy, June, 2006:172-177. [10]Boiko I, Fridman L, Pisano A, et al. Analysis of chattering in systems with second order sliding modes[J]. IEEE Transactions on Automatic Control, 2007, 52(11): 2085-2102. [11]Bartolini G, Pisano A, Punta E, et al. A Survey of applications of second-order sliding mode control to mechanical systems[J]. International Journal of Control, 2003, 76(9): 755-770.2 输出量y(t)抖振特性分析
3 广义DF法推导
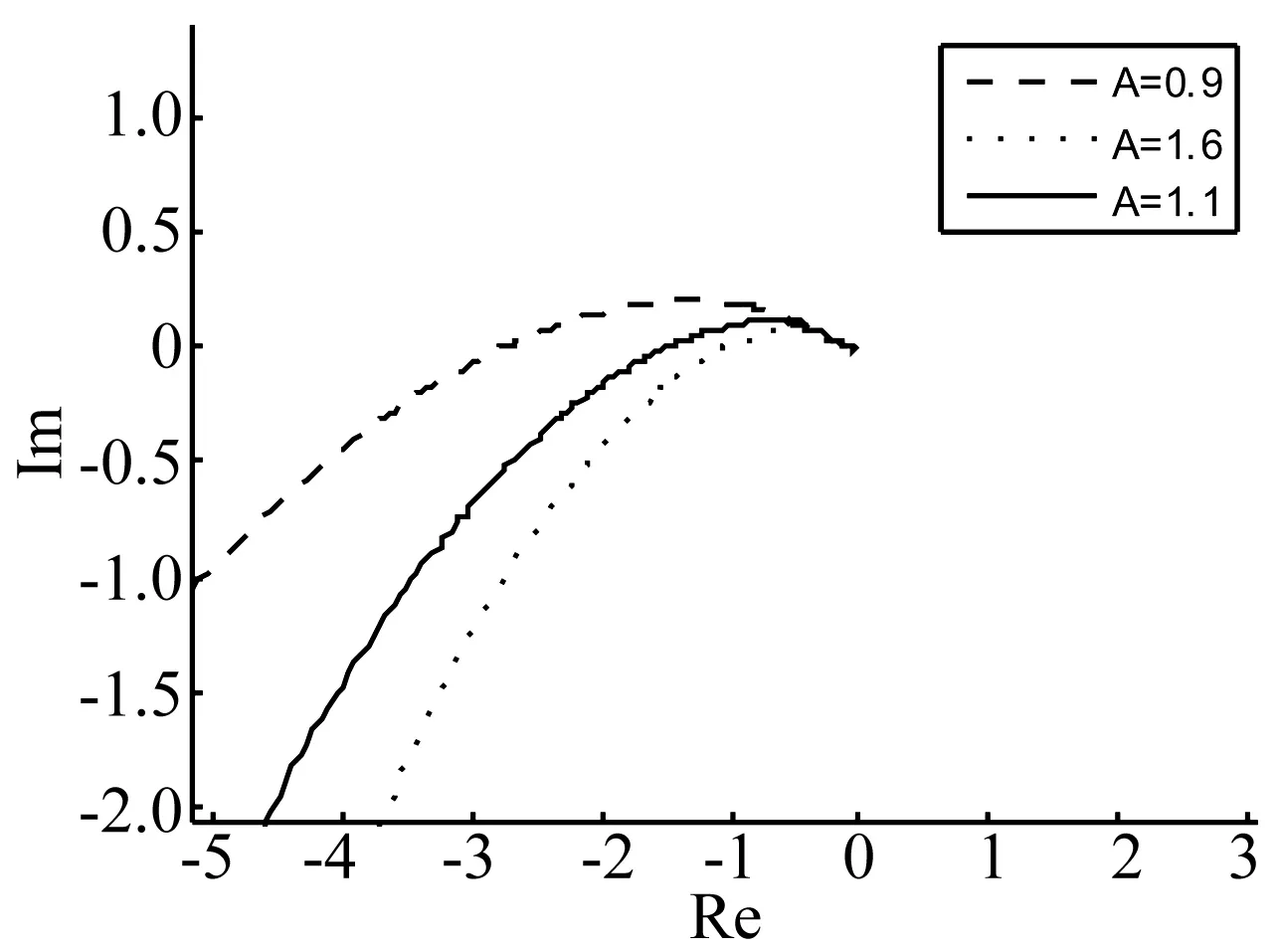
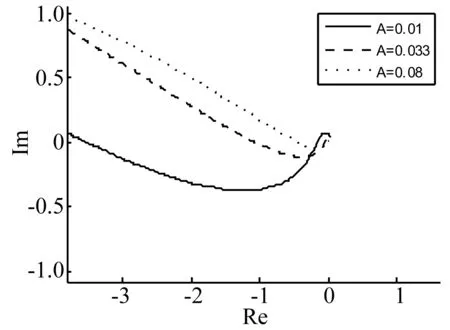
4 状态变量抖振特性分析
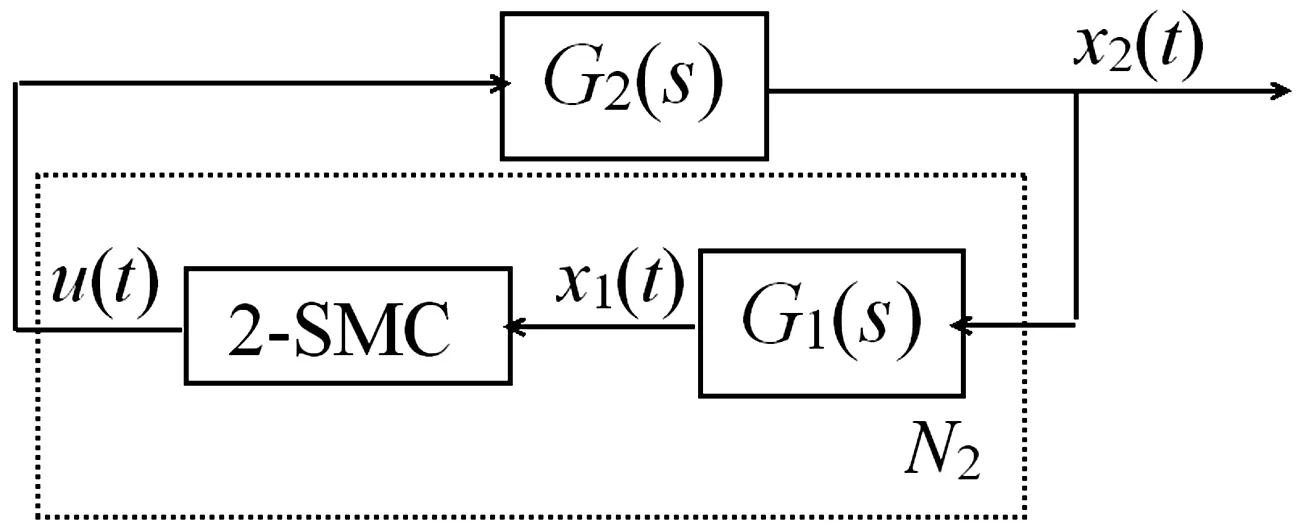
5 数值仿真实验
5.1 实验一
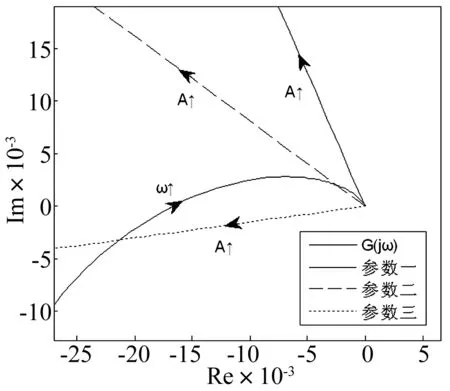
5.2 实验二

6 结 论

