低速冲击下金属面夹芯板性能分析

王洪欣，查晓雄，余 敏，王锦文

(1.哈尔滨工业大学 深圳研究生院, 广东 深圳 518055；2.筑博设计股份有限公司, 广东 深圳 518029)

金属面夹芯板以彩钢为面板，岩棉、聚氨酯等轻质材料为芯材，经连续成型工艺将芯材与面板粘结成整体的建筑用板材。夹芯板作为房屋的围护构件，在外物撞击下会产生显著变形甚至开裂，失去原有防护功能。随对意外事故下结构安全性重视，夹芯板抗冲击性能引起关注。Hazizan等[1]对表皮为无纺玻璃纤维、芯材为泡沫与蜂窝铝的夹芯梁抗低速冲击性能进行研究，所得能量平衡模型可较好分析低速冲击在弹性阶段的动力响应。Zhou等[2]分析简支圆形夹芯板在半圆形锤头低速冲击下的抗冲击性能。Nguyen等[3]采用显式有限元程序LS-DYNA及落锤实验装置对低速冲击下蜂窝铝夹芯板的动力响应进行研究，通过与实验数据对比，用LS-DYNA分析夹芯组合结构动力响应可信。Foo等[4]通过实验及有限元程序ABAQUS研究金属面蜂窝铝夹芯板抗低速冲击性能，其中铝材用双线性本构模型，所得冲击力与实验结果吻合较好。Abrate[5]概括夹心结构抗冲击模型，在分析夹芯板局部变形时，认为夹芯板置于刚性地面，将大量实验数据回归出冲击力峰值与凹陷变形间关系。查晓雄等[6]对钢混凝土组合结构的抗冲击能进行试验研究及数值模拟，获得到不同边界条件对构件受力性能影响。赵林虎等[7]进行碳纤维增强复合材料蜂窝夹芯结构冲击实验，获得多个频率冲击应力波在蜂窝夹芯结构中的传播速度。

以上为对玻璃纤维及FRP面材、泡沫铝芯材夹芯板的研究，而对金属面夹芯板抗冲击性能研究较少。本文用实验、有限元计算与理论分析相结合方法研究金属面夹芯板在落锤低速冲击下性能，为其耐撞性设计提供依据。

1 夹芯板冲击实验

1.1 实验介绍

冲击实验在DHR-9401落锤式冲击实验机上进行。实验机高13.47 m，撞击速度最高15.7 m/s，能满足大范围内低速撞击实验要求，轨道沿整个高度竖向误差仅2 mm，落锤下落较平稳，实验机见图1(a)。据每次实验前力传感器标定值，将电压幅值转化为冲击力时程曲线。落锤由锤头、力传感器及配重组成，锤头为半球形，见图1(b)。冲击彩钢夹芯板与铝合金夹芯板锤头半径分别为30 mm，80 mm，落锤质量分别为29.8 kg，32.3 kg。

金属面夹芯板由上下两层金属面板及内部芯材组成，试件面板类型有彩钢、铝合金两种，芯材类型有岩棉、聚氨酯两种；夹芯板彩钢面板厚度有三种类型：① 上下面板各0.7 mm，② 上下面板各0.5 mm，上面板0.7 mm，下面板0.5 mm；铝合金面板厚度为上下各0.7 mm；芯材厚度有50 mm，100 mm两种。夹芯板整体尺寸为1 200 mm×1000 mm×50 mm(100 mm)，沿长度方向两端简支，净跨1 000 mm，试件编号及材料参数见表1，构件的落锤冲击示意图，见图2。

图1 冲击实验装置

图2 实验构件冲击示意图

1.2 实验结果及分析

金属面夹芯板在落锤冲击下的变形、破坏方式可分为两种：① 上面板凹痕，落锤冲击处上面板产生局部凹陷，见图3(a)；② 上面板开裂，裂口呈四瓣形，见图3(b)。夹芯板在较大冲击能量下会产生整体变形，见图3(c)。

由实验看出：

(1) 随落锤冲击速度的增加，夹芯板所受冲击不断加大，夹芯板破坏程度愈加严重，面板由凹痕产生直至开裂。

(2) 夹芯板芯材厚度增加，夹芯板刚度增大；落锤以相同速度冲击时，夹芯板所受冲击力增大，如试件A-1-2(厚100 mm)在落锤速度6.57 m/s时所受冲击力大于试件A-2-1(厚50 mm)在落锤速度7 m/s时所受冲击力。

(3) 面板厚度增加，夹芯板刚度增大；落锤以相同速度冲击时夹芯板所受冲击力增大，如落锤以7.67 m/s速度冲击试件时，试件A-4-1所受冲击力大于试件A-2-2所受冲击力。

(4) 面板采用彩钢的抗冲击性能好于铝合金面板，如落锤以7.67 m/s速度冲击彩钢夹芯板A-4-1时，该试件仅面板产生凹痕，而落锤以6.1 m/s速度冲击铝合金夹芯板B-1-3时，其面板开裂破坏。

图3 面板破坏及整体变形

2 抗冲击有限元计算方法及验证

2.1 有限元建模

2.1.1 材料本构

金属面板与芯材所用线性弹塑性MAT_PLASTIC_KINEMATIC模型[8]参数为：密度RO，弹性模量E，泊松比PR，屈服强度σY，切线模量Etan。材料模型参数由试验获得，材料模型参数取值见表1。

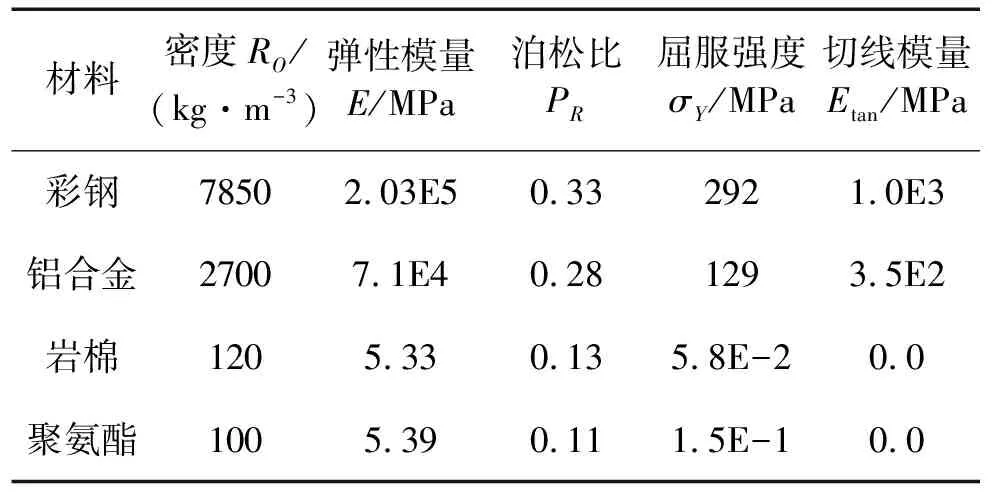
表1 材料模型参数及取值

2.1.2 网格划分

选择几何模型单元类型，主要根据材料几何形状及求解问题类型决定，且需综合考虑求解的收敛性。据金属面夹芯板构造，金属面板采用缺省4节点壳单元，上下面板各划分9 604个单元。芯材采用缺省的常应力8节点实体单元，模型共划分48 020个单元。为能反映出夹芯板构件冲击位置复杂受力及变形，对此处网格细化。落锤较夹芯板构件刚度大很多，故将落锤设为刚体材料，划分成2 340个单元。

2.1.3 边界及接触

金属面夹芯板受冲击时边界条件据实验设定，构件采用简支约束。落锤与夹芯板间接触方式采用单面自动接触(罚函数双向接触)，可处理接触过程中相互渗透问题，保证结果的有效性。软件中对应的关键字为*CONTACT_AUTOMATIC_SINGLE_ SURFACE。

2.1.4 其它参数设置

计算中，沙漏能过大会致结果误差较大，因此需查看整体模型的能量曲线，须控制沙漏能比例在可接受范围内，通常不超过内能的10%[9]。经分析，对夹芯板冲击应采用6号沙漏能控制，该沙漏能占总能量比重低于3%。

2.2 实验验证

采用有限元模型对上述夹芯板构件抗冲击性能进行数值模拟，其中典型构件冲击力时程曲线比较见图4；构件冲击力峰值有限元结果与实验结果比较见表2，两者比值的均值为1.048，方差为0.013。面板凹痕及开裂的有限元与实验结果比较见图5。计算结果表明，夹芯板抗冲击的有限元计算结果与实验结果吻合较好，该有限元模型可用于夹芯板抗冲击性能分析。

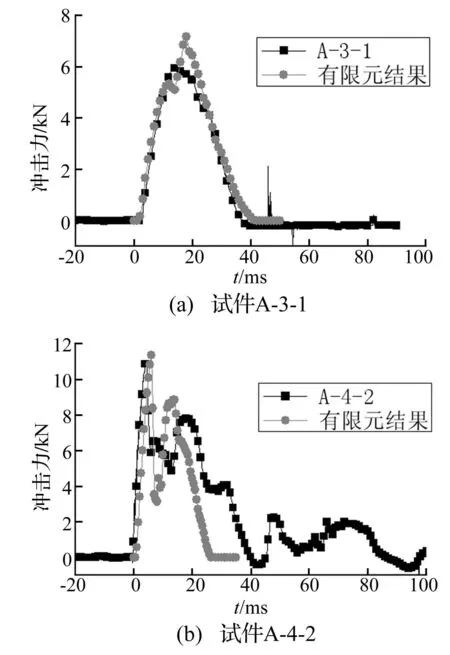
图4 冲击力时程曲线有限元结果与实验对比

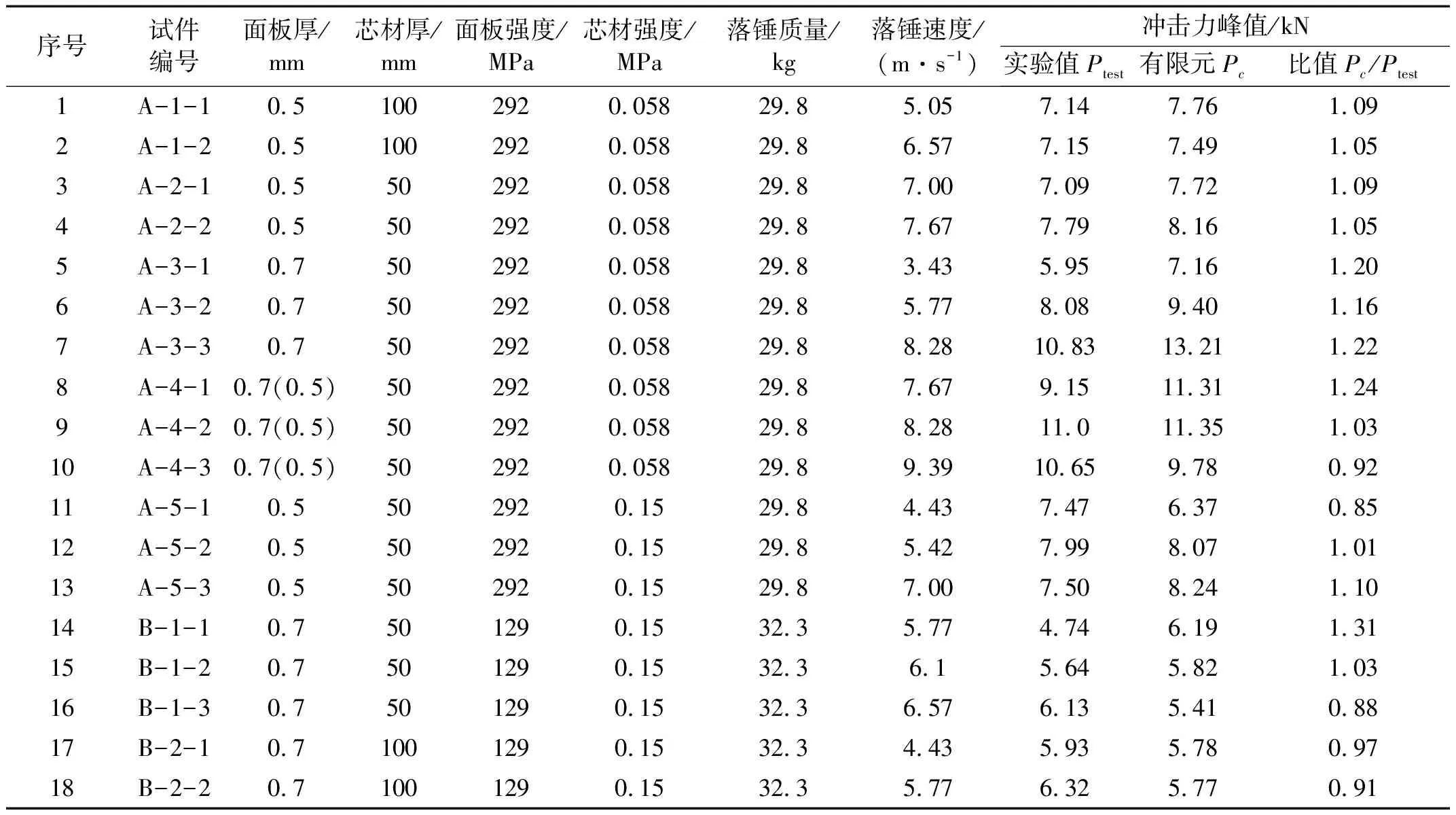
表2 冲击力及破坏的有限元与实验结果比较

图5 面板破坏的有限元与实验比较

3 夹芯板开裂冲击力

3.1 局部变形分析

分析夹芯板局部变形时，设夹芯板不产生整体变形，相当于夹芯板置于刚性地面。夹芯板局部变形包括上面板局部弯曲变形、局部拉伸变形及芯材压缩变形，夹芯板受落锤冲击的局部变形示意图见图6。

夹芯板在落锤冲击下，面板局部变形形函数[2]为

(1)

式中：RL为面板局部变形区域半径；wLmax为局部变形最大值。

图6 金属面夹芯板受落锤冲击局部变形示意

夹芯板局部变形势能UL，包括夹芯板上层面板局部弯曲变形势能、局部拉伸变形势能及芯材压缩变形势能，即

UL=ULB+ULS+ULC

(2)

式中：ULB为局部弯曲变形势能；ULS为局部拉伸变形势能；ULC为芯材压缩变形势能。

夹芯板上层面板局部弯曲变形势能[10]为

(3)

弯曲变形时，面板应变与变形关系为

(4)

面板弯曲变形势能为

(5)

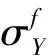
夹芯板上层面板局部拉伸变形势能[10]为

ULS=∫∫(Nxεx+Nyεy+Nxyγxy)dxdy

(6)

式中：Nx,Ny,Nz为面板平面内膜力，Nx=hfσx,Ny=hfσy,Nxy=hfτxy。

拉伸变形时，面板应变、变形关系为

(7)

面板拉伸变形能为

(8)

芯材压缩变形势能ULC为

(9)

冲击力做功为

(10)

将式(5)、(8)～(10)代入式(2)，得总势能为

(11)

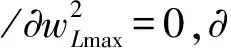
(12)

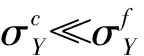
(13)

3.2 开裂冲击力

夹芯板受冲击时上层金属面板产生弯曲、拉伸局部变形，该变形较大时拉伸变形占主导，面板开裂破坏即为面板的拉伸断裂[12]；金属面板拉伸应变达到开裂应变εf时，发生开裂破坏。通过夹芯板的冲击实验及数值分析结果可知夹芯板面板开裂形式为辐射状，见图7。

图7 面板受冲击呈辐射状开裂破坏

夹芯板面板变形主要发生在冲击点至锤头半径范围内，结合式(1)得沿锤头半径方向变形伸长量为

(14)

面板拉伸断裂应变达到开裂应变εf的伸长量为

ΔLf=Rεf

(15)

联立式(14)、(15)，令ΔL=ΔLf，得面板开裂时局部变形值为

(16)

将式(13)代入式(16)，得面板发生开裂的冲击力Pf为

(17)

式中：εf为面板开裂应变。

建立有限元模型对夹芯板开裂冲击力式(17)的适用性进行验证。据式(17)知，影响金属面夹芯板开裂冲击力因素为面板强度、面板厚度、锤头半径及开裂应变等，同时，有限元模型中考虑落锤质量、速度、芯材强度、厚度对开裂冲击力影响。开裂冲击力计算值与有限元结果比较见表3。由表3看出，式(17)计算值与有限元结果比值均值为0.984，方差为0.016，表明式(17)计算结果适用。由计算知，金属面夹芯板开裂冲击力随面板强度、面板厚度、落锤半径、开裂应变的增加而增大，而落锤质量、芯材强度、芯材厚度的改变对开裂冲击力大小基本无影响；冲击体速度达到使面板开裂速度时，再增加冲击体速度，面板开裂冲击力也不会发生变化。

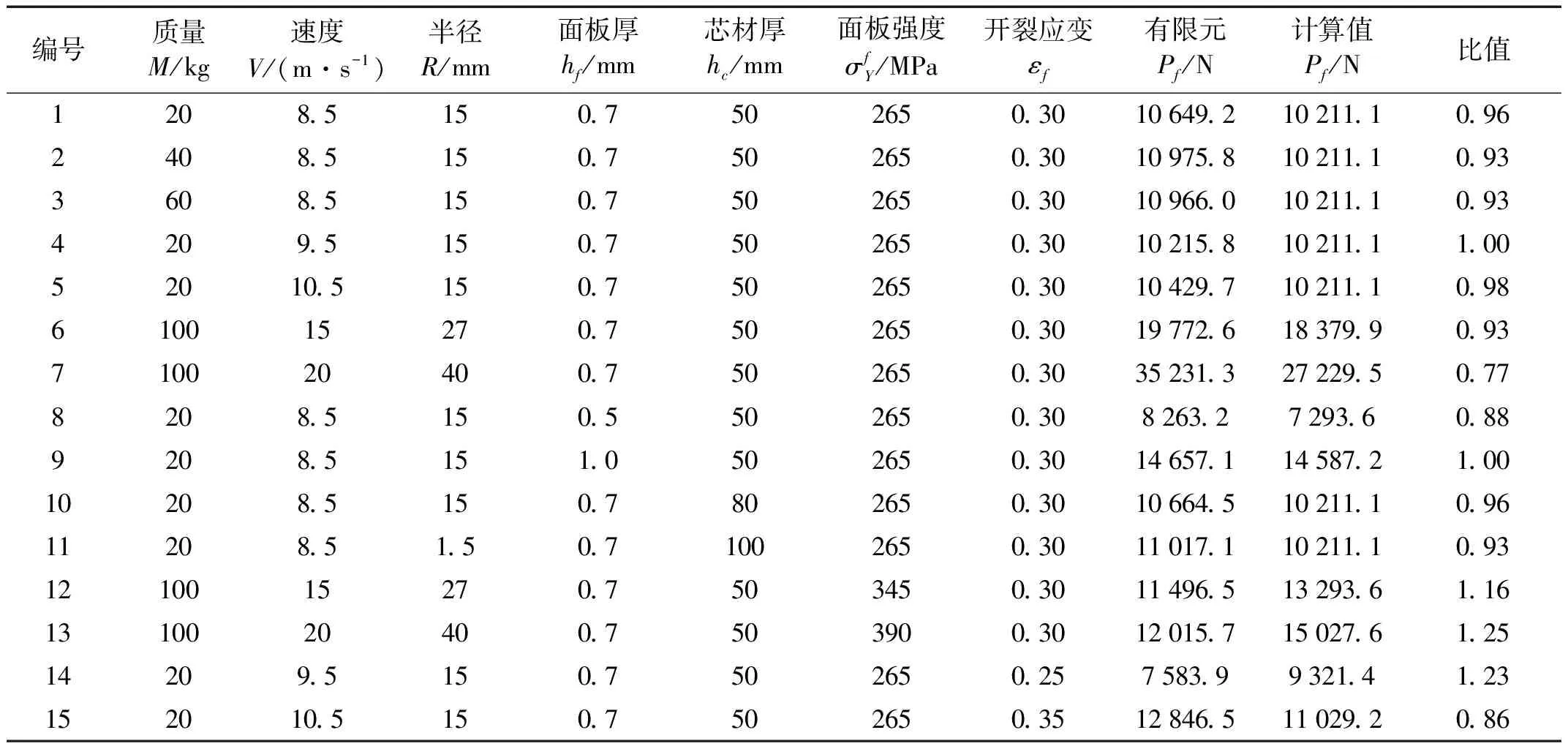
表3 夹芯板开裂冲击力计算值与有限元结果比较

4 结 论

(1) 本文用实验、有限元与理论分析相结合方法研究金属面夹芯板抗冲击性能。通过实验研究获得夹芯板在冲击下面板产生凹痕、开裂的破坏现象及夹芯板所受冲击力与落锤质量、落锤速度、面板厚度、芯材厚度等因素关系。并用有限元方法对实验进行模拟分析，有限元计算结果与实验结果吻合较好，验证有限元计算方法的适用性。

(2) 用理论分析方法对夹芯板局部变形进行分析，包括面板弯曲变形、拉伸变形、芯材压缩变形，据构件局部变形势能及外力做功建立总势能，并用势能驻值原理获得集中力与局部变形关系；以面板拉伸断裂为破坏条件，获得夹芯板开裂冲击力；建立有限元模型对夹芯板开裂冲击力计算式的适用性进行验证。有限元与理论分析表明，夹芯板开裂冲击力随面板强度、面板厚度、落锤半径、开裂应变的增加而增大，而落锤质量、芯材强度、芯材厚度改变对开裂冲击力大小基本无影响。

[1]Akil Hazizan M, Cantwell W J. The low velocity impact response of foam-based sandwich structures [J]. Composites PART B-Engineering,2002, 33(3): 193-204.

[2]Zhou D W, Stronge W J. Low velocity impact denting of HSSA lightweight sandwich panel [J]. International Journal of Mechanical Sciences,2006, 48(10): 1031-1045.

[3]Nguyen M Q, Jacombs S S, Thomson R S, et al. Simulation of impact on sandwich structures [J]. Composite Structures. 2005, 67(2): 217-227.

[4]Foo C C, Seah L K, Chai G B. Low-velocity impact failure of aluminum honeycomb sandwich panels[J]. Composite Structures. 2008, 85(1): 20-28.

[5]Abrate S. Modeling of impacts on composite structures [J]. Composite Structures. 2001, 51(2): 129-138.

[6]王洪欣,查晓雄,叶福相.空心钢管混凝土构件抗侧向冲击性能研究[J].华中科技大学学报(自然科学版),2010,38(8):107-110.

WANG Hong-xin, ZHA Xiao-xiong, YE Fu-xiang. Impact resistance of hollow concrete filled-steel tubular members subjected to lateral impact loading[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2010, 38(8): 107-110.

[7]赵林虎, 周丽. 复合材料蜂窝夹芯结构低速冲击位置识别研究[J].振动与冲击,2012,31(2):67-71.

ZHAO Lin-hu, ZHOU Li. Localization of low-velocity impact on a composite honeycomb sandwich structure[J].Journal of Vibration and Shock,2012,31(2):67-71.

[8]LS-DYNA Keyword User’s Manual [M]. Version971. California: Livermore Software Technology Corporation, 2006.

[9]赵海鸥. LS-DYNA动力分析指南[M]. 北京: 兵器工业出版社, 2003.

[10]刘士光,张涛. 弹塑性力学基础理论[M]. 武汉:华中科技大学出版社, 2008:241-242.

[11]龙驭球. 能量原理新论[M]. 北京:中国建筑工业出版社,2007.

[12]Hoofatt M S, Park K S. Dynamic models for low-velocity impact damage of composite sandwich panels-part a deformation [J]. Composite Structures, 2001, 52(3/4): 335-351.