铁路轨道几何数据冲击噪声小波-有序中值滤波方法
刘金朝,王卫东,孙善超,曲建军
(中国铁道科学研究院 基础所,北京 100081)
轨道几何不平顺为轮轨系统激扰源可导致机车振动,对行车安全性、平稳性、舒适性及环境噪声等均有重要影响。目前轨道几何参数动态检测主要采用惯性基准法,利用激光扫描、图像处理、惯性测量及数字信号处理技术,实现对轨距、轨向、高低、超高、水平、三角坑、曲率等轨道几何参数的实时采集与处理[1-2]。由于外界阳光反射干扰、传感器及数据传输误差等原因,铁路轨道几何不平顺检测数据中常存在冲击噪声。冲击噪声产生局部异常大值,易对轨道状态形成错误超限判断。因此应在超限判断、计算轨道质量指数、轨道不平顺谱等状态指标前自动剔除,但目前轨道检测系统主要靠人工删除。靠经验剔除冲击噪声存在两问题,即效率低与评判结果多样性。用轨道检测系统动态监测轨道状态,为及时消除轨道几何检测数据中冲击噪声,检测人员需实时跟踪、编辑检测数据,耗时、耗力。此外,因检测人员经验、水平不同,对超限大值及冲击噪声的分辨能力存在较大差别,所给评判结果不一致。
滤除信号中冲击噪声在过程控制[3]、声音信号处理[4]、图像处理[5]中经常碰到。近20年来对此已有较深入研究,并提出诸多处理方法,如线性滤波法、中值滤波法[5-8]、模糊滤波法[9-11]、自适应滤波法[4,12]等。Itagaki[4]提出的处理图像冲击噪声的自适应滤波方法,通过多步迭代提高信号的信噪比;Claudio等[12]在进行信号谱密度估计时提出用线性优化方法自适应降低冲击噪声影响。由于铁路轨道几何数据冲击噪声的特殊性,现有方法尚不能直接利用。线性滤波法为一种全局滤波器,若对信号所有样本点进行处理会破坏未被污染的样本性质、降低信号质量。自适应滤波法虽能有效降低冲击噪声影响,但算法过于复杂、计算量过大,较难满足轨道几何数据冲击噪声的实时处理需要。
通过比较分析含冲击噪声、道岔处大轨向及大值超限处轨道几何信号频率分布发现,冲击噪声一般分布在轨道几何信号高频部分,而大轨向、大值超限成分一般分布在信号低频部分。称小波分析为信号分析数学显微镜,在时频平面不同位置具有不同分辨率,高频时用短窗口,低频时用宽窗口,为多分辨率分析方法。结合轨道几何信号频率分布与小波变换的多分辨率性质,将信号分解成两部分:①含冲击噪声的高频部分,②正常的低频部分。利用有序中值方法(ROM)自动识别高频信号中冲击噪声位置并滤波。
1 小波-有序中值滤波方法
由冲击噪声突变特性知,冲击噪声分布于信号高频部分。基于该性质提出铁路轨道几何数据冲击噪声的小波-有序中值滤波方法。该方法分两步完成:即将信号分解成高、低频部分,再据信号样本与相邻样本相似性自动识别冲击噪声位置并处理。小波-有序中值滤波实现过程为
(1) 利用多分辨率分析,将轨道几何不平顺信号S分解为高频部分Sh及低频部分Sl:
S=Sh+Sl
(1)
(2)利用有序中值方法(ROM)自动识别高频部分Sh中冲击噪声并处理:
Sh=Sh0+Shi
(2)
(3)将不含冲击噪声的高、低频信号叠加得滤波信号S0:
S0=Sh0+Sl
(3)
式中:Sh0为滤除冲击噪声的高频信号。
1.1 离散小波分解
有多种方式可将信号分解成含冲击噪声的高、低频部分。选择离散小波分解方法主要因小波变换具有数学显微镜特性。通过离散小波变换,可清楚分辨冲击噪声分布的高频段。
轨道几何不平顺信号S(t)∈L2(R)的连续小波变换可表示为
(4)
式中:
(5)
式(5)可由母小波ψ(t)经平移、放缩获得。实际应用中通常将ψab(t)中连续变量a,b取整数离散形式为
ψj,k(t)=2j/2ψ(2jt-k)
(6)
小波变换表示为离散小波变换为
WS(j,k)=[S(t),ψj,k(t)]
(7)
给定轨道几何不平顺信号S(t)及双尺度方程传递系数h={h0,h1,…,hL-1},g={g0,g1,…,gL-1},利用金字塔算法[13]可快速计算获得离散小波变换系数;通过重构,得轨道几何不平顺信号S(t)多分辨率逼近:
(8)
式中:N为离散小波分解水平数;di(i=1,2,…,N)为各水平的高频分量;aN为第N水平的低频分量。高通传递系数h={h0,h1,…,hL-1}及低通传递系数g={g0,g1,…,gL-1},满足关系式gi=(-1)i+1hL-1-i,(i=0,1,…,L-1)。
由式(8)可将信号高频部分Sh及低频部分Sl定义为
(9)
1.2 有序中值滤波方法
采用有序中值方法(ROM)自动识别高频分量Sh中冲击噪声并处理。记Sh0为未被冲击噪声污染的高频信号。在概率意义下,Sh0与Sh满足关系:
(10)
式中:η(n)为独立同分布的随机过程。
基于上述假设,据Sh(n)与相邻样本相似性自动识别冲击噪声位置,并用相邻样本的有序中值代替冲击噪声Sh(n)。定义长度Lw滑动窗为W。一般Lw取奇数,Lw=7时滑动窗见图1。

图1 滑动窗
在n时刻对Sh(n)加窗,并取窗内除Sh(n)外其它元素为观察样本:
w(n)=[w1(n),w2(n),w3(n),
w4(n),w5(n),w6(n)]=
[Sh(n-3),Sh(n-2),Sh(n-1),
Sh(n+1),Sh(n+2),Sh(n+3)]
(11)
按上升方式对w(n)进行排序,得:
r(n)=[r1(n),r2(n),r3(n),
r4(n),r5(n),r6(n)]
(12)
定义差分识别器为
(13)
式中:μ(n)=[r3(n)+r4(n)]/2为有序中值。
若d(n)大于某预先设定的阈值T,则判定Sh(n)为冲击噪声,并令Sh(n)=μ(n)。由工程经验知,轨道不平顺相邻两点变化率一般不会大于3‰,轨道几何信号采样长度为 0.25,由此设定阈值T=0.75 mm。为提高算法效率,上述算法采用递推方式,图1中窗内左边3个值Sh(n-j)(j=1,2,3)为更新后的值。
2 试验验证
通过对含冲击噪声的模拟信号及实测信号进行滤波,分析验证小波-有序中值方法的滤波性能。为与其它滤波方法比较,选具有解析解的周期性不平顺及冲击噪声叠加所得模拟信号进行滤波,比较分析不同滤波结果的信噪比与均方误差。在轨道几何检测数据中滤除轨向不平顺数据中冲击噪声较困难,因其既含冲击噪声又含道岔处有用的大轨向信息,其幅值均为大值。利用小波-有序中值方法对实测高速铁路轨向不平顺数据进行滤波,分析验证其实用性。
2.1 模拟信号滤波分析
含冲击噪声的周期性模拟信号件图2,其中周期性信号可写为
w0(t)=3sin10πt
(14)

图2 模拟不平顺信号、冲击噪声信号及其合成信号
将小波-有序中值滤波方法与中值滤波法、小波滤波法、有序中值滤波法比较。中值滤波法虽简单,但广泛用于冲击噪声滤波分析,并作为标准比较方法。而有序中值滤波法通常认为是有效处理冲击噪声的滤波方法。本文方法为以其为基础发展获得。通过比较可看出新方法特点及优势。选择信噪比SNR及均方误差MSE为定量比较指标:
(15)
式中:wu(t)为未被污染的原始周期信号(图2(b)),wf(t)为滤波后信号。
利用小波变换将信号分解为高、低频两部分,结果见图3。不同小波基与分解水平数对结果会产生一定影响。由试算选Daubechies 4为小波基,分解水平数取5。利用有序中值方法(ROM)滤除图3(a)高频信号中冲击噪声,结果见图4。图4(a)实线为原始周期信号,虚线为滤波后信号,图4(b)为二者之差。由图4看出,滤波后信号与原始周期信号几乎完全重合,表明新滤波方法能完整还原周期性不平顺信号。
以图2(c)冲击噪声位置为中心,取长度21个点6段比较不同分析方法的滤波性能。分别计算各段原始周期信号及4种滤波方法所得滤波信号的信噪比 SNR与均方误差 MSE,结果见表1。由表1看出,小波-有序中值信噪比远大于其它3种方法,均方误差 MSE远小于其它方法。小波方法最差,说明直接利用小波方法滤除冲击噪声不合适。在冲击噪声附近,有序中值滤波略好于中值滤波,若同时考虑其它未被冲击噪声污染的样本,有序中值滤波较中值滤波更有效。因中值滤波为整体滤波方法,会改变所有样本点;而有序中值及小波-有序中值能据其与相邻样本的相似性识别冲击噪声位置,并只对被噪声污染的样本进行修正。
2.2 实测信号滤波分析
利用小波-中值有序方法对实测的高速铁路轨向不平顺数据进行滤波分析,结果见图5。图5(a)实线为实测的轨向不平顺数据,虚线为滤波后结果;图5(b)为二者之差。实测信号长度近 225 km,90 万个样本点,滤波时间小于10 s,表明该方法可在线运行。由图5(a)看出,多处位置出现大值,分别对应冲击噪声和道岔处大轨向信息。由图5(b)看出,大值冲击噪声只有两处。因此,小波-中值有序方法能正确识别冲击噪声位置并修正。

表1 不同方法滤波结果比较分析
图5中A-A区段局部放大信号见图6。高速铁路无砟轨道一般采用 18号道岔,并在道岔处将轨距加宽至15 mm。利用轨距信息分辨冲击噪声及道岔处大轨向信息。由图6(b)轨距信号可知,A-A区段恰为道岔区,轨距加宽致轨道中心发生变化,由激光摄像系统采集的轨距及轨向不平顺幅值突然变大,表征轨距加宽为有用信息非冲击噪声。由图6(a)、(b)看出,在用小波-中值有序方法进行滤波处理过程中,道岔A2 处已完整保留大轨向信息;A1 处已保留大轨向信息,而叠加在其上的冲击噪声被滤除。道岔A1,A2 处轨向不平顺信号具有不同特征因为其开口方式不一致。
图5中B-B区段局部放大信号见图7。由图7(c)轨距信号可知,该区段未出现加宽轨距,为非道岔区,图7(a)的突变大值为冲击噪声。由图7(b)的信号差看出,小波-中值有序方法只对被冲击噪声样本进行处理,其它样本无任何改变,说明该方法能成功识别冲击噪声位置并滤除,且不改变未被冲击噪声污染的样本质量。
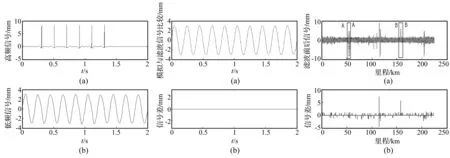
图3 模拟信号的高、低频分解信号

图6 A-A区段局部轨道几何不平顺信号及滤波信号

图7 B-B区段局部轨道几何不平顺信号和滤波信号
3 结 论
(1) 铁路轨道几何数据中冲击噪声不仅影响轨道质量指数、轨道不平顺谱等轨道状态参数计算,且易产生错误的报警信息,应在检测过程中自动删除。本文结合两种传统的噪声滤波方法,提出铁路轨道几何数据中的冲击噪声的小波-有序中值滤波方法。据冲击噪声高频特性,利用小波变换的多分辨率性质,将信号分解成含冲击噪声的高、低频两部分,再利用有序中值方法自动诊断、滤除高频信号中的冲击噪声。与其它经典冲击噪声滤波方法相比,本文方法具有简单、高效、强健等优势,且可在线实现。
(2) 本文所提冲击噪声自动滤除方法具有较好推广前景及应用价值,可用于其它基础设施检测数据,如车辆动力学响应数据、弓网几何检测数据等预处理分析,计算速度快,不仅可在地面运行,也可在线实现,并准备将该方法集成到基础设施地面中心的数据分析软件与轨道检测系统中。
[1]Coenraad E. Modern railway track [M]. Duisburg, Germany: MRT-productions, 1989.
[2]宁静,诸昌钤,张兵.基于EMD和Cohen核的轨道不平顺信号分析方法[J].振动与冲击,2013,32(4):31-38.
NING Jing,CHU Chang-qian,ZHANG Bing.An approach for signal analysis of track irregularity based on EMD and Cohen’s kernel[J].Journal of Vibration and Shock, 2013, 32(4):31-38.
[3]Zhu Y. Multivariable system identification for process control[M]. Amsterdam:Pergamon, 2001.
[4]Itagaki H.Improvements of nuclear magnetic resonance image quality using iterations of adaptive nonlinear filtering[J]. IEEE Trans. Med. Imag., 1993, 12(2):322-327.
[5]Chandra C, Moore M S, Mitra S K. An efficient method for the removal of impulse noise from speech and audio signals[J]. Proc. IEEE Int. Symp. Circuits Syst., Monterey, CA, 1998(4):206-208.
[6]Abreu E, Lightstone M, Mitra S K,et al. A new efficient approach for the removal of impulse noise from highly corrupted images [J]. IEEE Trans. Image Process., 1996, 5(6):1012-1025.
[7]Moore M S, Mitra S K. Performance analysis of the two-state signal-dependent rank order mean filter[J]. Proc. 10th SPIE, Nonlinear Image Process., San Jose, CA, 1999, 3646: 56-66.
[8]Yin L, Yang R, Gabbouj M, et al. Weighted median filters: a tutorial[J]. IEEE Trans. Circuits Syst.,1996, 43(3):157-192.
[9]Naso D, Scalera A, Aurisicchio G, et al. Removing spike noise from railway geometry measures with a fuzzy filter[J]. IEEE Transactions on Systems, Man and Cybernetics-Part C: Applications and Reviews, 2006, 36(4):485-494.
[10]Russo F. Impulse noise detection and filtering using fuzzy models[J]. Proc. 17th IEEE Instrum. Meas. Technol. Conf., 2000(2):1041-1044.
[11]Zhang D, Wang Z. Impulse noise detection and removal using fuzzy techniques[J]. IEE Electronics Letters,1997, 33(5):378-379.
[12]Claudio E D D, Orlandi G, Piazza F, et al. An improved LS algorithm for the estimation of an impulsive noise corrupted signal by linear programming [J]. Proc. IEEE Int. Symp. Circuits Syst., 1991, 1:714-717.
[13]Mallat S. A theory of multi-resolution signal decomposition: the wavelet representation[J]. IEEE Trans. PAMI, 1989,11: 674-693.

