考虑球面副间隙的并联机构动力学模型
王庚祥,刘宏昭, 邓培生
(西安理工大学 机械与精密仪器工程学院,西安 710048)
并联机构因承载能力强、刚度大、精度高等优点而成为研究热点。早期并联机构为Stewart[1]平台。随并联机构与空间机构在航空领域的发展[2-3],对精确预测系统动力学行为要求愈加迫切,且相关理论研究不断发展。如并联机构运动学研究、动力学研究、奇异位形分析、刚度分析及性能评价[5-9]。但对并联机构中关节间隙研究相对较少。
运动副是构成并联机构多刚体系统的重要组成部分。由于关节元素间的磨损,局部变形、瑕疵及制造误差会导致运动副中存在间隙;而间隙为保证关节元素相对运动与装配的必要条件。因此,若运动副中不存在间隙将导致机构关节锁死,无法装配。关节中间隙的存在不仅改变运动副构件间自由度及受力状态,且当关节处于分离状态时产生的碰撞与冲击力将造成磨损加剧,噪声及振动会导致机构丧失精度,降低使用效率及寿命[9]。
关节间隙对机构动力学性能影响研究主要集中于平面机构分析[10-15]。但随空间机构的应用广泛及迅速发展,对关节间隙研究转向空间[9,16-21]。本文考虑球面副间隙,基于连续接触模型,将球面副间隙视为刚性无质量杆[11,17-18,21],利用牛顿-欧拉法建立4-SPS/CU并联机构[22]含关节间隙的动力学模型。为该并联机构作为重型作战车辆上的导弹发射跟踪装置提供理论依据,考虑关节间隙可改善4-SPS/CU并联机构动力学性能,提高其控制精度。
1 4-SPS/CU并联机构结构特点
4-SPS/CU机构模型[22]及坐标系建立见图1。设驱动支链A1B1与下平台相连的球面副(铰点B1)含有间隙。

图1 4-SPS/CU并联机构简图
2 含关节间隙并联机构动力学建模
运动副间隙描述方法有4种,即动量平衡法、接触变形模型、有限元法及连续接触模型[9,23]。由于并联机构自身动力学模型具有强非线性,可避开运动副中刚度系数、阻尼系数、摩擦系数及恢复系数等物理参数简化含间隙机构动力学建模;由于含间隙关节元素分离、碰撞时间较短,可设运动副元素间始终处于连续接触状态。
2.1 球面副间隙模型
4-SPS/CU并联机构的驱动支链中含球面副与移动副,而约束从动支链中含万向铰与圆柱副,而本文只对B1球面副间隙量进行研究,由于① 球面副位于该并联机构的驱动支链上,相比约束支链的运动副,考虑球面副间隙更能体现关节间隙对该并联机构输入、输出参数影响;② 为简化原动力学模型而未选择驱动支链与上平台相连的球面副。因此本文采用连续接触模型视球面副间隙[24]为一刚性无质量杆-间隙杆。
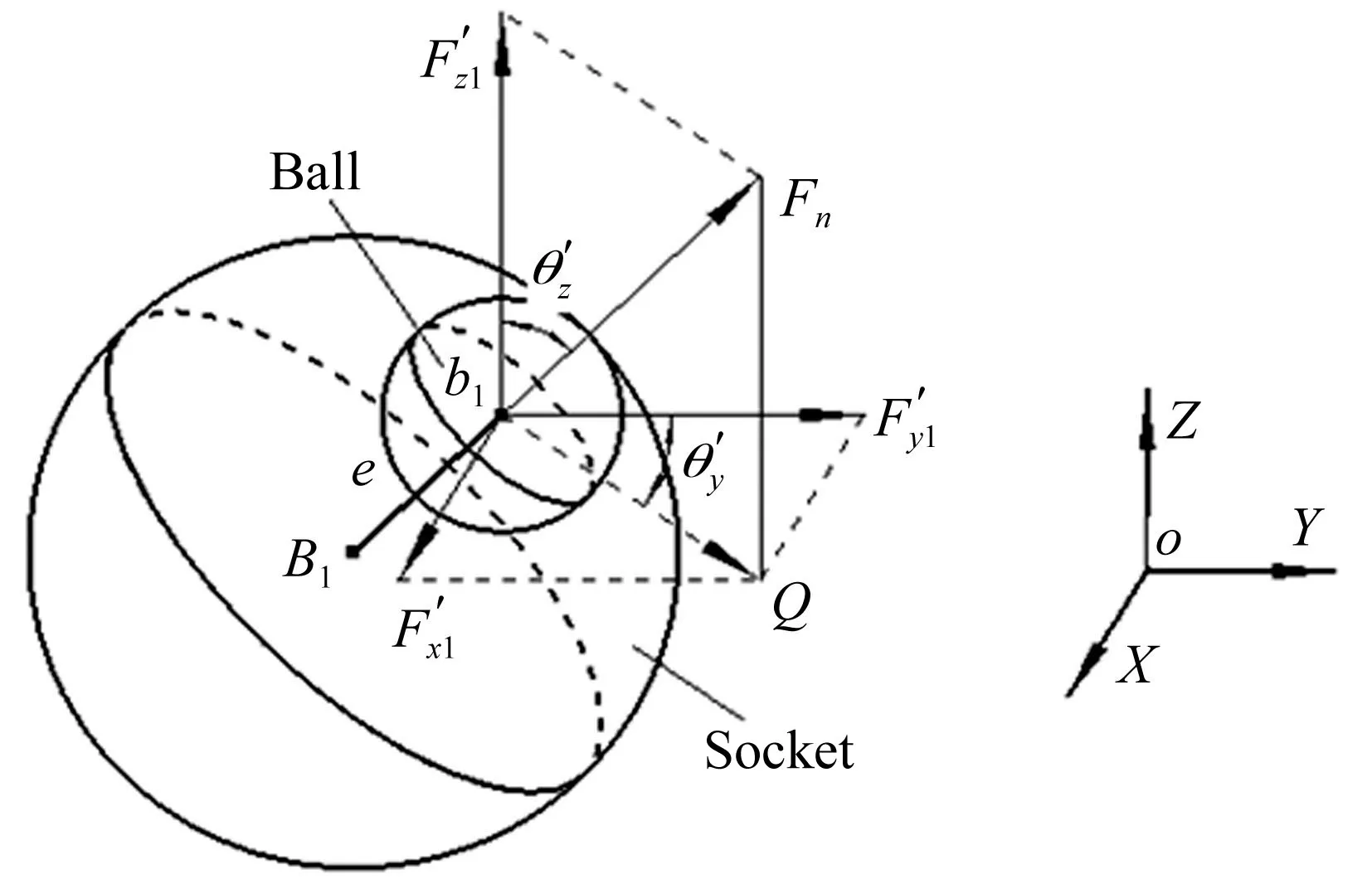
图2 球关节间隙模型
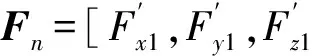
(1)
(2)
2.2 考虑球面副间隙的并联机构位置方程
由于4-SPS/CU并联机构为无过约束机构,且理想运动副下SPS驱动支链[22]为不受约束的6自由度刚体。当驱动支链B1铰点处考虑球面副间隙时,原3个转动自由度的球面副被引入3个移动自由度,即该支链在固定坐标系OXYZ的螺旋表示为
(3)
式中:p1,q1为下球铰(SPS支链与下平台连接的球面副)相对坐标系OXYZ位置;u1,v1,w1为移动副轴线方向余弦;l1,m1,n1为上球铰(SPS支链与下平台连接的球面副)相对于坐标系OXYZ位置;$1,$2,$3为下球铰转动自由度螺旋表示;$4为移动副螺旋表示;$5,$6,$7为上球铰转动自由度螺旋表示;$11,$12,$13为下球铰考虑间隙新引入3个移动自由度的螺旋表示。
设式(3)螺旋系反螺旋为
$r=(LrMrNr;PrQrRr)
(4)
基于互易积原理建立方程:
$ij∘$r=0, (i=1,2,3,…,7,j=1,2,3)
(5)
对该线性方程求解后得方程无解,该螺旋系无反螺旋,即该含间隙的驱动支链与理想支链自由度保持一致。4-SPS/CU并联机构[22]中无论考虑任何球面副含有间隙均不改变该机构上平台自由度。
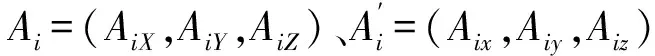
(6)
式中:i=1,2,3,4。
考虑球面副间隙的4-SPS/CU并联机构相比式(6)只有驱动支链l1的位置方程发生改变,其它支链位置方程保持不变。驱动支链l1位置方程为
(7)
2.3 4-SPS/CU并联机构理想运动学方程
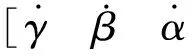
(8)
(9)
式中:
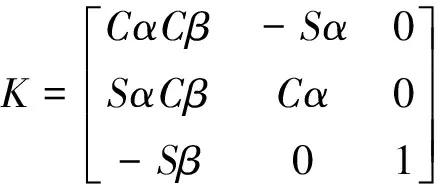
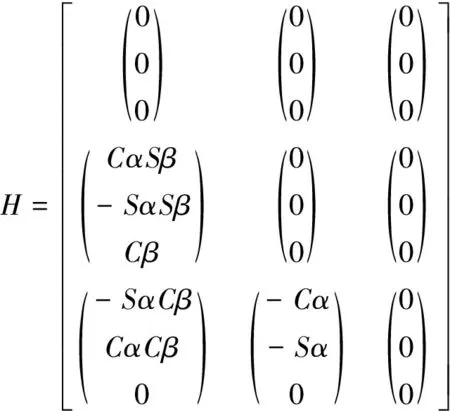
2.4 理想4-SPS/CU并联机构的动力学分析
为简化4-SPS/CU并联机构动力学模型,将驱动支链作整体研究,求驱动支链质心位置[25]:
(10)
式中:m1为驱动杆质量;m2为缸体质量;m为驱动支链质量;lsi为驱动杆质心至动铰点Ai距离;lmi为缸体质心至固定铰点Bi距离;li为驱动支链总长(随时间变化);lci为驱动支链质心距固定铰点Bi距离;i=1,2,3,4。
2.4.1 驱动支链受力分析
由于SPS驱动支链含局部自由度,为避免其对该驱动支链动态静力学平衡方程结构影响[25]。需对驱动支链在固定坐标系OXYZ与局部坐标系Biuiviwi中方位进行分析[25]。坐标系OXYZ相对Biuiviwi的转换矩阵为
R(αiZ,θiX)=[RZαi][RXθi]=
(11)

驱动支链在固定坐标系OXYZ中具体受力分析见文献[25]。驱动支链在固定坐标系OXYZ中绕固定铰点Bi作纯转动的角速度为
(12)
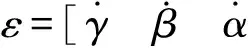
ηi=pilciSi
(13)
驱动支链处于动态平衡时,力平衡方程为
(14)
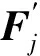
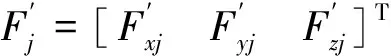
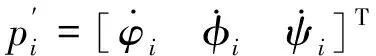
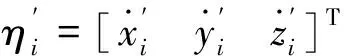
在局部坐标系Biuiviwi对驱动支链固定铰点Bi取矩,力矩平衡方程为
(15)
据研究结论[25],驱动支链力矩平衡方程因局部自由度需去掉绕Z轴转动力矩平衡方程,则式(15)去掉多余后,在固定坐标系OXYZ下力矩平衡方程为
(16)
2.4.2 恰约束从动支链受力分析[25]
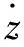
(17)
对下平台质心O取矩,力矩平衡方程为
(18)
2.4.3 上平台受力分析[25]
上平台质心OXYZ在固定坐标系角速度ω=[ωxωyωz]T,上平台在动坐标系Pxyz的各转动惯量为I′,则上平台相对固定坐标系OXYZ的转动惯量为
I=RI′RT
(19)
式中:

当上平台处于动态平衡时,力平衡方程为
(20)
对上平台质心O点取矩,力矩平衡方程为
(21)
联立式(14)、(16)~(18)、(20)、(21)组成(6×6-4)维方程组Γ中含(6×4+8)个未知力/力矩。方程组Γ的矩阵表示记为AX=B,A为由4-SPS/CU并联机构结构参数与旋转角组成的系数矩阵;B为由该并联机构重力/力矩与外载荷及系统惯性组成的已知矩阵;X为由该机构所有运动副反力组成的未知量矩阵X=A-1B。
2.5 含球面副间隙的驱动支链动力学分析
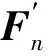
(22)
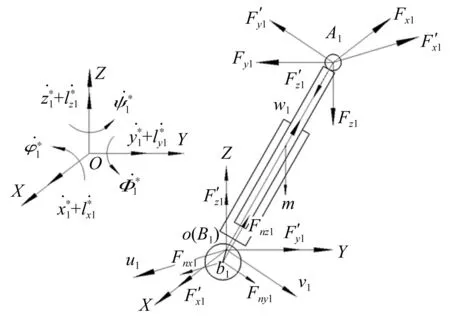
图3 4-SPS/CU并联机构间隙杆动态静力分析
固定坐标系OXYZ下驱动支链l1力平衡方程为
(23)
在局部坐标系Biuiviwi对驱动支链固定铰点B1取矩,力矩平衡方程为
(24)
同理,据式(16)写出式(24)去掉多余后在固定坐标系OXYZ下力矩平衡方程为:
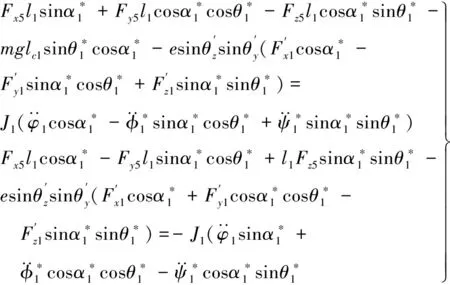
(25)

考虑该并联机构球面副关节间隙后,该机构驱动力为
(26)
2.5.1 含关节间隙动力学方程求解
(1) 不考虑球面副间隙时,方程组Γ记为AX=B。通过该方程求出4-SPS/CU并联机构关节约束反力/力矩X=A-1B,记关节约束反力为X1。
(27)
(28)
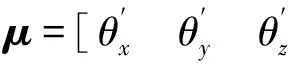
(3) 将(2)中结论代入式(7)、(6)中并对该并联机构运动学进行分析,导出所有含关节间隙的运动学参数,获得关节间隙对该并联机构运动学影响,为动力学分析奠定基础。

2.6 数值计算
4-SPS/CU并联机构设计参数、间隙参数见表1。
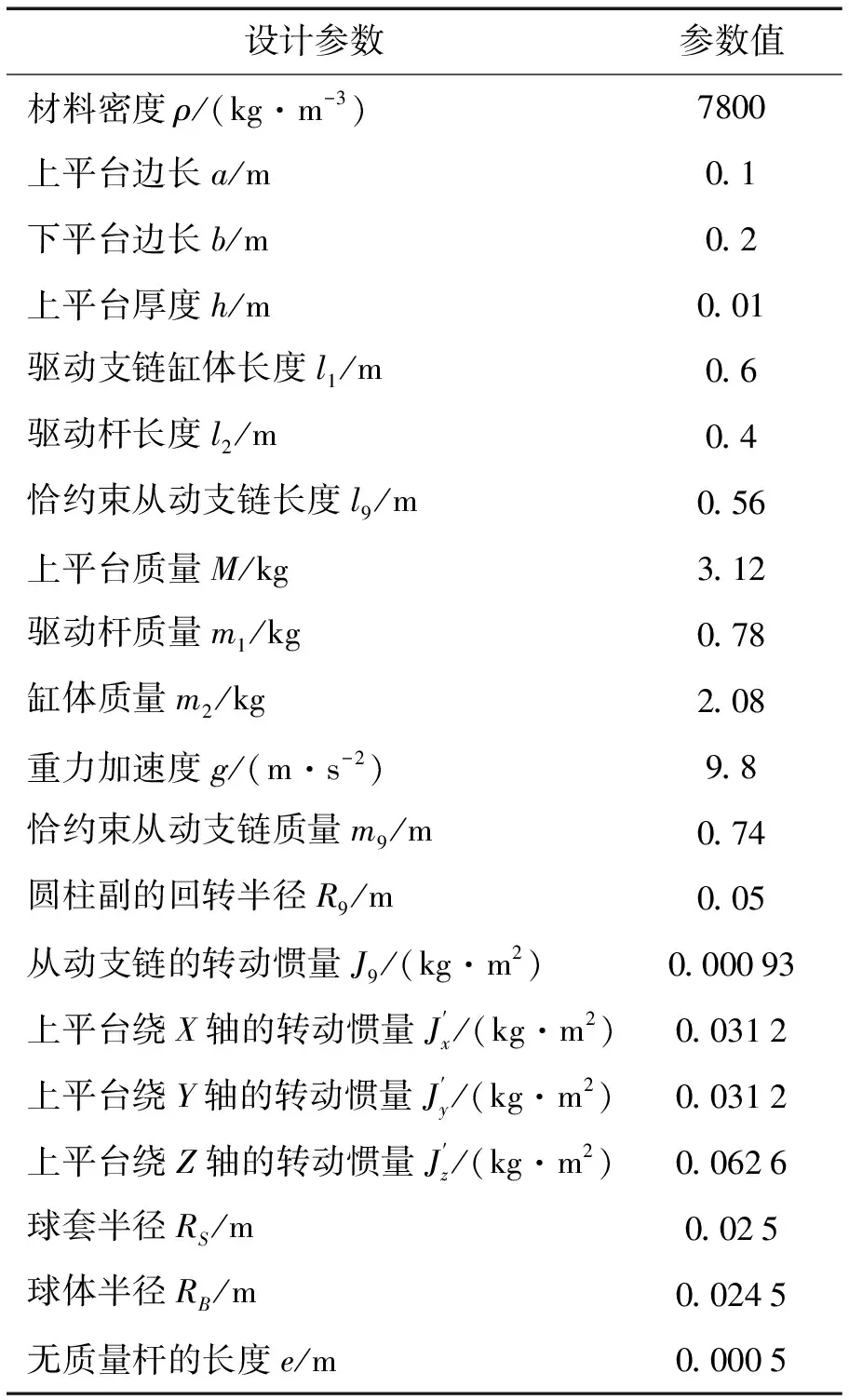
表1 结构参数
设上平台不受外力情况下,质心P点运动规律为
(29)
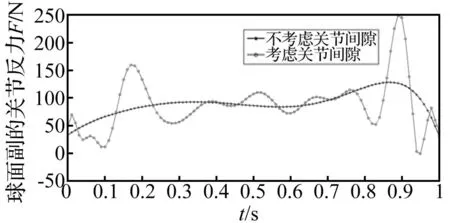
图4 B1处球面副受力分析
4-SPS/CU并联机构B1点处球面副考虑关节间隙与不考虑关节间隙时对比分析曲线见图4。由图4看出,时间处于0.1 s,0.95 s附近时,含间隙球面副关节反力小于等于0,说明含间隙球面副元素发生分离;时间处于0.2 s,0.9 s附近时,含间隙球面副关节反力为理想关节副反力的2~3倍,说明含间隙球面副元素发生碰撞;时间处在0.3~0.8 s时,考虑间隙与不考虑间隙对球面副关节反力影响不大,说明该机构球面副元素处于接触状态。因此,可利用该方法判定B1点处球面副元素接触分离状态。
关节间隙对4-SPS/CU并联机构驱动支链长度与驱动速度影响曲线见图5。由图5知,关节间隙对驱动支链长度与驱动速度均有影响,且对驱动速度影响较明显。由于关节间隙位置角为该机构运动学参数函数,当上平台速度增加时,关节间隙对驱动支链长度、驱动速度影响越显著,图中数值分析与理论研究相吻合。

图5 驱动支链运动学分析
4-SPS/CU并联机构考虑间隙与不考虑间隙时驱动力对比分析曲线见图6。由图6看出,以无质量杆代替B1处球面副关节间隙,对该机构驱动力无明显影响。原因为本文视球面副间隙为无质量杆避免因间隙导致的接触碰撞力,忽略间隙接触体刚度系数、阻尼系数、摩擦系数及碰撞过程中能量损失。因此,球面副间隙对该并联机构驱动力影响较弱。
3 结 论
(1) 以无质量杆代替4-SPS/CU并联机构中球面副间隙。建立球面副间隙模型及该机构含间隙铰时的位置方程。令间隙量为零研究理想机构运动学,并基于达朗贝尔原理建立该机构动态静力学方程,求出该机构所有关节副反力。设含间隙运动副反力位置角与无间隙运动副反力位置角近似相等,对4-SPS/CU并联机构中无质量杆进行运动学分析。
(2) 通过对含关节间隙驱动支链重新受力分析,写出该支链含球面副间隙动态平衡方程,结合理想机构动态平衡方程组装考虑关节间隙时的动力学方程HX′=K。给出该方程的求解过程。通过数值方法对比分析该机构在考虑间隙与不考虑间隙时驱动力与关节反力及利用该机构含间隙位置方程研究其运动学反解,获得连续接触模型中关节间隙对该机构的驱动力影响不明显,而对该机构运动学特性影响显著。
[1]Gough V E, Mech E M I, Whitehall S G,et al.Universal tyre test machine[C]. in: Proceedings of Ninth International Technical Congress,F.I.S.I.T.A.,1962:117-137.
[2]Zhao Yang, Bai Zheng-feng.Dynamics analysis of space robot manipulator with joint clearance[J].ActaAstronautica,2011,68(7-8): 1147-1155.
[3]Li Tuan-jie, Guo Jian, Cao Yu-yan.Dynamic characteristics analysis of deployable space structures considering joint clearance[J].Acta Astronautica,2011,68(7/8):974-983.
[4]Jaime G A ,Agust n R A ,H ctor R G ,et al.Kinematics of an asymmetrical three-legged parallel manipulator by means of the screw theory[J].Mechanism and Machine Theory,2010,45(7):1013-1023.
[5]Staicu S, Zhang D.A novel dynamic modelling approach for parallel mechanisms analysis[J].Robotics and Computer-Integrated Manufacturing,2008,24(1):167-172.
[6]Amine S, Masouleh M T,Caro S,et al.Singularity analysis of 3T2R parallel mechanisms using grassmann-cayley algebra and grassmann geometry[J].Mechanism and Machine Theory,2012,52:326-340.
[7]Pashkevich A, Chablat D, Wenger P.Stiffness analysis of overconstrained parallel manipulators[J].Mechanism and Machine Theory,2009,44(5):966-982.
[8]Wang Jin-song, Wu Chao, Liu Xin-jun.Performance evaluation of parallel manipulators: motion/force transmissibility and its index[J].Mechanism and Machine Theory,2010,45(10):1462-1476.
[9]Shiau T N, Tsai Y J, Tsai M S.Nonlinear dynamic analysis of a parallel mechanism with consideration of joint effects[J].Mechanism and Machine Theory,2008,43(4):491-505.
[10]kErkaya S, Uzmay I.Determining link parameters using genetic algorithm in mechanisms with joint clearance[J]. Mechanism and Machine Theory,2009,44(1):222-234.
[11]Tsai M J,Lai T H.Kinematic sensitivity analysis of linkage with joint clearance based on transmission quality[J].Mechanism and Machine Theory,2004,39(11):1189-1206.
[12]Flores P, Ambrosio J.Revolute joints with clearance in multibod y systems[J].Computers and Structures, 2004, 82(17/19): 1359-1369.
[13]Wang Jin-ge, Zhang Jun-fu, Du Xiao-ping.Hybrid dimension reduction for mechanism reliability analysis with random joint clearances[J].Mechanism and Machine Theory,2011,46(10):1396-1410.
[14]Muvengei O, Kihiu J, Ikua B.Numerical study of parametric effects on the dynamic response of planar multi-bodysystems with differently located frictionless revolute clearance joints[J].Mechanism and Machine Theory,2012,53:30-49.
[15]Bai Zheng-feng, Zhao Yang.Dynamicbehaviour analysis of planar mechanical systems with clearance in revolute joints using a new hybrid contact force model[J].International Journal of Mechanical Sciences,2012,54:190-205.
[16]Huang T, Chetwynd D G, Mei J P,et al.Tolerance design of a 2-DOF overconstrained translational parallel robot[J].IEEE Transactions on Robotics, 2006,22(1):167-172.
[17]Parenti-Castelli V, Venanzi S. Clearance influence analysis on mechanisms[J].Mechanism and Machine Theory,2005, 40(12):1316-1329.
[18]Chebbi A H, Affi Z, Romdhane L.Prediction of the pose errors produced by joints clearance for a 3-UPU parallel robot[J]. Mechanism and Machine Theory,2009,44(9):1768-1783.
[19]Frisoli A, Solazzi M, Pellegrinetti D,et al.A new screw theory method for the estimation of position accuracy in spatial parallel manipulators with revolute joint clearances[J].Mechanism and Machine Theory,2011,46(12):1929-1949.
[20]Chaker A, Mlika A, Laribi M A,et al.Clearance and manufacturing errors' effects on the accuracy of the 3-RCC spherical parallel manipulator[J].European Journal of Mechanics A/Solids,2013,37:86-95.
[21]Bu Wang-hui, Liu Zhen-yu, Tan Jian-rong, et al.Detachment avoidance of joint elements of a robotic manipulator with clearances based on trajectory planning[J].Mechanism and Machine Theory,2010,45(6):925-940.
[22]王庚祥,原大宁,刘宏昭.空间4-SPS/CU并联机构运动学分析[J].农业机械学报,2012,43(3):207-212.
Wang Geng-xiang,Yuan Da-ning,Liu Hong-zhao. Kinematics analysis of spatial 4-SPS/CU parallel mechanism[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(3):207-212.
[23]阎绍泽,陈鹿民,季林红,等.含间隙铰的机械多体系统动力学模型[J].振动工程学报,2003,26(3):290-294.
YAN Shao-ze,CHEN Lu-min,JI Lin-hong,et al. Dynamie modeling of multibody system with clearanceJoints[J]. Journal of Vibration Engineering, 2003,16(3):290-294.
[24]Tian Qiang, Zhang Yun-qing, Chen Li-ping, et al.Dynamics of spatial flexible multibody systems with clearance and lubricated spherical joints[J].Computers and Structures,2009,87(13-14):913-929.
[25]王庚祥,刘宏昭,原大宁.空间4-SPS/CU并联机构的受力分析[J].农业工程学报,2012,28(22):30-38.
WANG Geng-xiang, LIU Hong-zhao, YUAN Da-ning. Force analysis of spatial 4-SPS/CU parallel mechanism[J].Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(22): 30-38.

