离心泵流体激励力诱发的振动：蜗壳途径与叶轮途径

蒋爱华，李国平，周 璞，章 艺，华宏星

(1．中国船舶重工集团公司 第704研究所，上海 200031；2．上海交通大学 机械系统振动国家重点实验室，上海 200240)

流体激励力为离心泵振动原因之一，研究其诱发离心泵整个系统振动，对减小振动传递至其它设备、板壳结构所致设备故障、辐射噪声有重要意义[1]。流体力主要通过两条途径引起离心泵系统振动，泵内表面-蜗壳-支架-基座及叶轮-转轴-支撑-基座。

虽有诸多对离心泵流体激振研究，但多集中于离心泵内流场CFD计算[2-3]、空化对离心泵振动影响[4-5]、流体激励作用下离心泵振动稳定性分析[6-7]、叶轮-蜗舌间隙对离心泵流体激振试验[8]、人体内离心血泵减振研究[9-10]、不同工作介质对离心泵振动影响[11]等方面。亦有对运转过程中蜗壳、叶轮流体力变化的研究[12-13]，但由蜗壳、叶轮两途径分析流体力所致系统振动及所诱发振动的相互关系并不明确，因此在低振动等级离心泵设计中仍无降低系统流体激振有效方法。因此，本文尝试基于离心泵叶轮与蜗壳的流体激励力[12-13]，建立泵内表面-蜗壳-机架系统有限单元模型，瞬态响应分析获得蜗壳途径流体激励力诱发的系统振动，建立叶轮-转轴-支撑-机架转子动力学模型，瞬态响应分析获得叶轮途径流体激励力诱发的系统振动，并对比分析流体力两途径所致系统振动。由于主要关注两途径振动对比，故仅以垂直于离心泵机架方向振动为研究内容。

1 离心泵流体激振力分析

取单级单吸六扭曲叶片离心泵为研究对象，叶轮外径172 mm，额定工况比转速139，额定转速2930 r/min(48.83 Hz)，额定流量100 t/h。设计离心泵系统试验台架见图1，坐标原点位于离心泵蜗壳对称平面与叶轮轴线交点处，垂直于离心泵机架方向为X，Y，Z。

电机通过非接触式电磁联轴器带动模拟轴系(模拟实际电机离心泵安装)与离心泵叶轮转动，离心泵通过管道吸水并送回水箱；离心泵、模拟轴系与电机安装在同一机架上，机架通过8个隔振器安装于刚性基础；离心泵进出口通过波纹管与管道连接以隔离管道振动，使电机-模拟轴系-离心泵-机架成为独立振动系统；电磁联轴器仅传递扭矩、消除电机转轴与模拟轴系不对中所致系统振动；通过动平衡技术减小电机主轴质量不平衡。

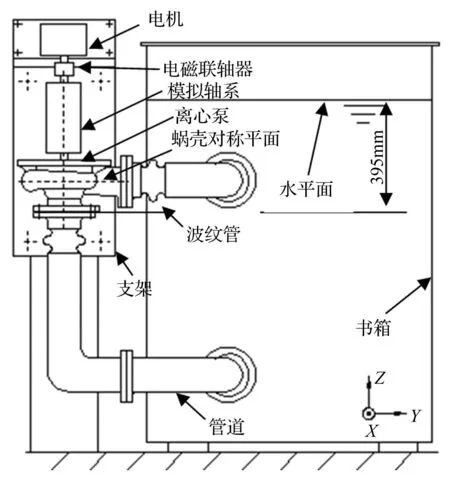
图1 离心泵安装示意图

图2 离心泵流体力计算结果

以叶轮每转动2°为一时间步，用CFX分析离心泵额定工况转动一周共180个时间步的瞬态流场。计算时进口边界条件为静压3 871 Pa(即395 mm水柱)，出口边界条件设置为流量，湍流采用SST模式，底层网格Yplus值小于11.63，以确保其位于对数率层内，其余流域几何建模、参数设置方法、计算过程与结果验证等见文献[12-13]。由流场计算获得蜗壳内表面、叶轮各表面流体力，并通过积分获得叶轮空间3方向流体合力与合力矩。第一时间步蜗壳内表面、叶轮表面流体绝对压力分布见图2(a)，叶轮空间X方向流体合力与功率谱见图2(b)，轴(Z)向流体力绕Y轴流体合力矩与功率谱见图2(c)。

2 蜗壳途径流体激励力诱发的振动

2.1 电机-离心泵-机架系统FEM模型建立

3.1.1 实际结构简化与建模

据离心泵系统实际安装与具体结构，建立电机-离心泵-机架-隔振器系统有限元模型见图3，其中泵体、模拟轴系外壳及二者连接机架用实体solid45单元；泵内表面用surf154单元以从流场计算软件CFX中读入各时间步流体力(图3(c))；泵、模拟轴系与电机共同机架用壳体shell63单元；每个隔振器用3个弹簧combine14单元，且Y、Z方向刚度设无穷大，以关注X向振动。泵叶轮、模拟轴系主轴等简化为附加质量，并通过改变主轴承处单元密度保持总质量不变(图3(a))；电机作为附加质量采用同样处理方法，即改变电机安装处机架密度以保持整个系统质量不变(图 3(e))，系统共分6个区域。

表1 各单元网格数量

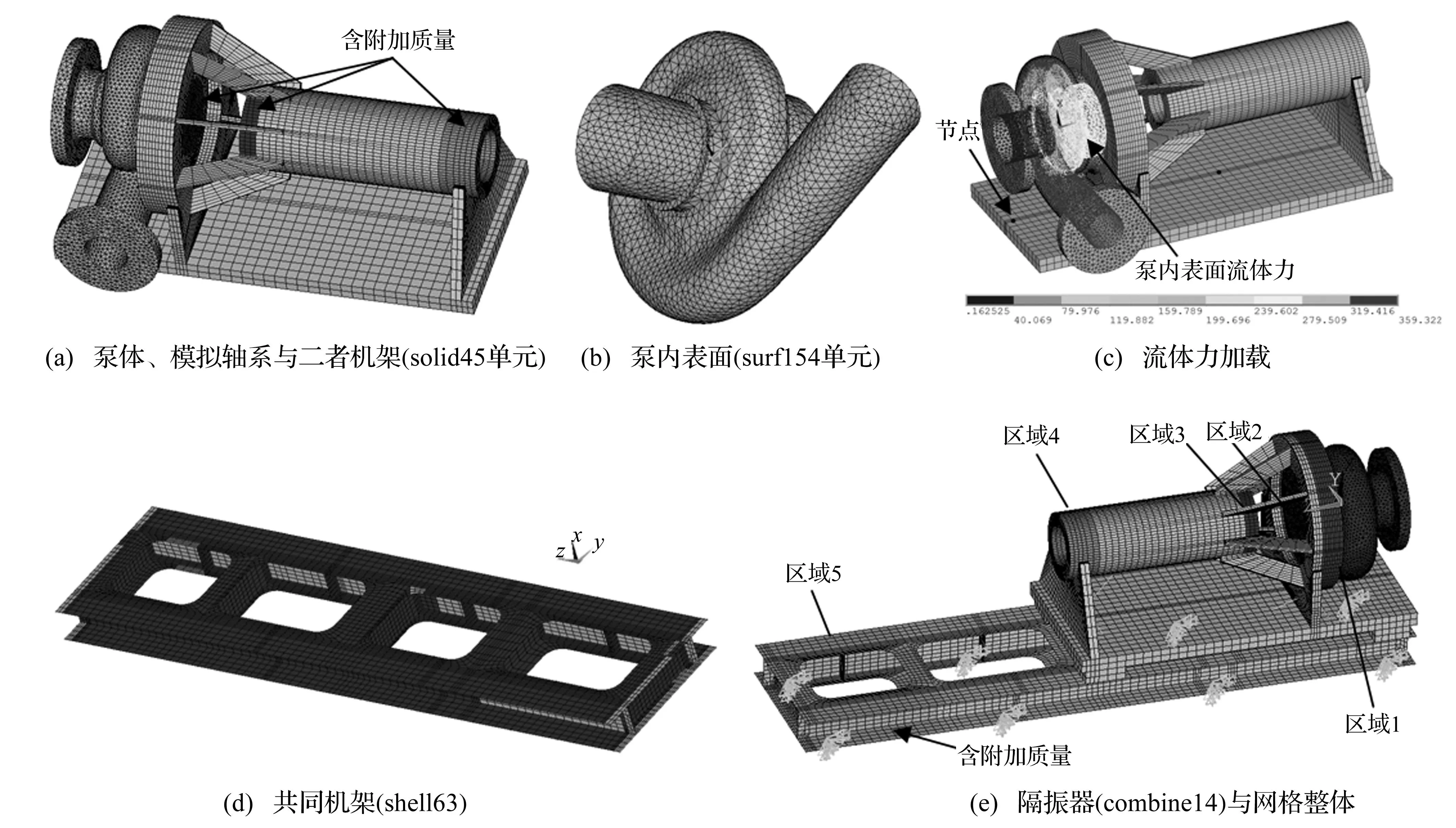
图3 电机-离心泵-机架系统有限元模型

3.1.2 参数设置

模型主要参数设置见表2。combine14刚度设为所用隔振器BE85X向真实刚度3.77 E5 N/m。

表2 不同区域材料属性

3.1.3 模型验证

对所建有限元模型进行模态分析，并基于锤击法用LMS对共同机架进行模态测试，计算获得振型、固有频率与测试结果基本一致，由此认为所建模型有效。

计算所得前10阶固有频率件表3。

表3 前10阶固有频率

2.2 流体激励瞬态响应分析

基于所建FEM模型与流场计算结果，在Ansys中通过APDL语言读入泵内表面180个时间步流体力并加载，瞬态响应分析加载方式为：零时刻FEM模型各节点受力、初始位移设为0；第1载荷步长设10 s，线性斜坡加载，所加载荷为CFX第1时间步泵内表的流体力；第2载荷步与第1载荷步相同，时间步长5 s；各载荷步用CFX 中对应时间步结果，并周期性重复加载，载荷步长与CFX 中各时间步长相同，即1.1366E-4 s，相邻两载荷步间均用线性斜坡加载，共902个载荷步，即叶轮转动5圈。

采用此加载方式即为避免第1载荷步加载过程产生冲击响应无法消除。所建FEM模型未考虑阻尼作用，泵内表面各节点受力由零通过加载变为第1时间步的流体力相当于一冲击激励，其响应始终存在于系统振动中。因此设定较长第1载荷步加载时间，其响应频率会较低，通过滤出低频振动信号方法可消除其影响。第1载荷步为10 s时，需滤除0.1 Hz以下信号。用Ansys对系统瞬态响应进行分析，用Ansys中Full算法计算。

2.3 泵内表面流体力诱发的振动

计算得泵内表面流体激励力作用下叶轮转动5圈中电机-离心泵-机架-隔振器系统各节点振动位移及加速度，并运用巴特沃斯3阶高通滤波器滤除45 Hz以下信号(泵内表面流体激励力频率均高于叶轮转频48.83 Hz)，见图4，节点具体位置见图3(c)。由图4看出，主要频率除叶片通过频率293 Hz外，亦含89 Hz、127 Hz、200 Hz、319 Hz及348 Hz等固有频率处波峰值，泵内表面流体压力脉动为宽频激振源，会使离心泵系统产生各阶模态振动。其余节点位移、加速度相同。

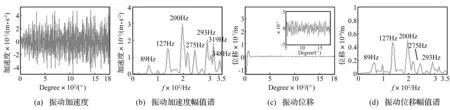
图4 节点振动加速度及振动位移

3 叶轮途径流体激励力诱发的振动

3.1 叶轮-转轴-支撑-机架转子动力学模型建立

3.1.1 叶轮-转轴-支撑-机架系统模化

据离心泵实际结构，建立叶轮-转轴-支撑-机架转子动力学模型，见图5。图5(a)为含各转动部件的模拟轴系，包括叶轮、轴套1、轴套2、转轴与电磁联轴器，该轴系通过轴承1、轴承2、模拟电机壳体安装在机架上。将轴系模化为四圆盘-三轴段-两支撑的转子动力学模型，见图5(b)。电磁联轴器、叶轮直径远大于转轴直径，因此将其考虑成质量圆盘m1，m4，将轴承、转轴简化成轴承处两圆盘m2，m3；转子与支架间用滚珠轴承连接，因其阻尼小而简化为弹簧kx2，kx3，因隔振器阻尼较小，忽略其阻尼作用；泵体、模拟轴系外壳、泵体与轴系外壳机架、电机、共同机架简化为转子动力学模型中基座m0；隔振器简化为弹簧并将基座m0与刚性基础连接；建模时忽略转子扭转振动、剪切效应与圆盘陀螺力矩，仅研究转子弯曲振动。

3.1.2 动力学方程建立

图5(c)、(d)、(e)分别为转子动力学模型圆盘、轴段、机架受力情况分析。基于达朗伯原理建立转子模型动力学方程为

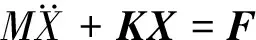
(1)

式中：X为系统自由度向量；M为质量矩阵；K为刚度矩阵；F为激励力向量。具体形式为

X=[x1θ1x2θ2x3θ3x4θ4x0]T

F=[0 0 0 0 0 0Fx4Mx40]T

图5 转子系统模化、各部件受力分析与轴承刚度测量

式中：xi，ki分别为圆盘i位移、转角；Fx4，Mx4分别为叶轮上流体力、力矩；mi，Ji分别为圆盘i质量与绕径向转动惯量；fi=li/EiIi，li为轴段i长度；kx0为8隔振器并联刚度；kx2，kx3为轴承支撑刚度。

3.1.3 参数确定

据实际结构尺寸简化得式(1)各参数见表4。用配重法近似测量kx2，kx3，并以图5(f)中光电位移传感器为零相位参考，通过振动位移峰值相位确定两端轴承处等效偏心质量相位后，分别在其相位处安装配重，通过轴系带动配重旋转产生的激振力与增加配重前后振动位移幅值差的比值得出轴承支撑刚度。联轴器端轴承刚度约等于两倍离心泵端轴承刚度，与离心泵端采用一个轴承、联轴器端采用两个轴承的实际结构相符。

表4 刚度测试结果

3.2 转子动力学模型瞬态响应分析

将泵叶轮X方向流体力与绕Y轴流体合力矩加载至转子动力学模型中进行瞬态响应分析。加载方式与蜗壳途径流体力瞬态响应分析相同，即用10 s为第1载荷步加载时间，并保持该载荷5 s，再循环加载流场计算各时间步所得载荷。用Newmark-β隐式算法可获得转子动力学方程的收敛解。计算叶轮转动100圈共18 000个时间步中系统振动响应，用Buttworth 6阶滤波器对所得结果进行滤波，滤出45 Hz以下信号。

3.3 叶轮流体力诱发的振动

图6(a)、(b)分别为计算所得叶轮转动10圈共3 600个时间步、滤波后基座振动位移与幅值谱，图6(c)、(d)为基座振动加速度与幅值谱。由图6看出，在流体激励作用下转子系统基座位移在各阶转动频率处均有峰值出现；其中位移最大峰值出现在叶轮转动频率48.8 Hz处，第二大峰值出现在5倍转频244.2 Hz处，亦即流道通过频率(6叶片叶轮中共5个流道)，而叶片通过频率293 Hz处位移峰值则相对较小。基座加速度最大峰值出现于流道通过频率244.2 Hz处，第二大峰值出现于转频48.8 Hz处，而叶频293 Hz处峰值相对较小。

4 蜗壳途径与叶轮途径诱发振动对比

图7(a)、(b)为计算所得流体力通过蜗壳与叶轮两途径基座的振动位移及加速度，图7(c)～(f)为两途径基座振动叠加计算结果、测试结果及幅值谱，测试结果见图5(f)中4个测点振动位移与加速度算术平均值。由图7(a)、(b)看出，流体力通过蜗壳途径诱发的基座位移与加速度远小于通过叶轮途径诱发的基座位移与加速度。 由图7(c)看出，计算所得基座位移与测试结果波形较相似，但计算结果小于测试结果。由图7(d)看出，计算与测试位移幅值谱最大峰值出现于叶轮转动频率48.8 Hz处，计算结果与测试值在100 Hz以下频段相似性较好。由图7(e)看出，计算得加速度幅值与测试值基本相同。由图7(f)看出，计算与测试所得加速度最大峰值均位于流道通过频率244.2 Hz处。

由计算、测试结果的相似性证明，计算结果的正确性、所提支撑刚度测试方法的可行性以及所建转子动力学的准确性。

图6 基座振动位移及加速度

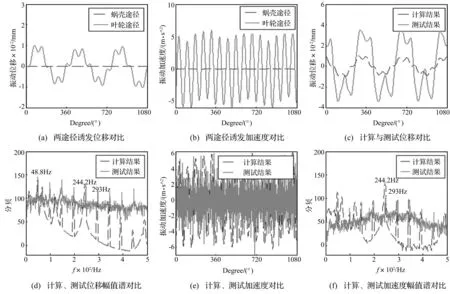
图7 两途径诱发基座振动与计算、测试基座振动

5 结 论

(1) 泵内表面流体压力脉动是宽频激振源，会诱发离心泵系统产生各阶模态振动。

(2) 流体力通过叶轮途径诱发离心泵基座振动位移幅值谱最大峰值出现于叶轮转频处，加速度幅值谱最大峰值出现于叶轮流道通过频率处，而非叶片通过频率处。

(3) 流体力通过蜗壳途径诱发离心泵基座振动远小于通过叶轮途径诱发的振动，叶轮-转轴-支撑-机架为流体激励诱发离心泵基座振动的主要途径。

(4) 由两条传递途径分别研究流体力所致振动以确认流体激励离心泵振动主要途径方法有效可行。

(5) 建立转子动力学模型时考虑陀螺力矩作用将使计算所得离心泵系统振动更接近测试值。

[1]蒋爱华,张志谊,章艺,等. 离心泵噪声研究的综述和展望[J].振动与冲击,2011,30(2):77-84.

JIANG Ai-hua,ZHANG Zhi-yi,ZHANG Yi,et al.Review and outlook of studying noise of centrifugal pumps[J]. Journal of Vibration and Shock,2011,30(2):77-84.

[2]Lucius A,Brenner G. Unsteady CFD simulations of a pump in part load conditions using scale-adaptive simulation[J]. International Journal of Heat and Fluid Flow,2010(6): 1113-1118.

[3]Hyun P S, Gerald L M. Centrifugal pump pressure pulsation prediction accuracy dependence upon CFD models and boundary conditions[C]. Proceedings of the ASME Fluids Engineering Division Summer Conference, Part A, 2009: 207-220.

[4]Diang H, Visser F C, Jiang Y,et al.Demonstration and validation of a 3D CFD simulation tool predicting pump performance and cavitation for industrial applications[J]. Journal of Fluids Engineering, Transactions of the ASME,2011,133(1): 011101-011113.

[5]Ni Yong-yan,Yuan Shou-qi,Pan Zhong-yong, et al. Detection of cavitation in centrifugal pump by vibration methods[J]. Chinese Journal of Mechanical Engineering, 2008(5): 46-49.

[6]白长青, 许庆余, 张小龙. 密封和内阻尼对火箭发动机液氢涡轮泵转子系统动力稳定性的影响[J].机械工程学报,2006,42(3):150-155.

BAI Chang-qing,XU Qing-yu,ZHANG Xiao-long. Effects of seal and internal damping on dynamic stability of liquid hydrogen turbopump rotor system in rocket engine[J]. Chinese Journal of Mechanical Engineering, 2006,42(3):150-155.

[7]田爱梅, 朱梓根.涡轮泵转子稳定性计算[J].推进技术, 2000, 21(3):43-45.

TIAN Ai-mei,ZHU Zhi-gen.Calculation for rotor stability in turbopumps[J]. Calculation for Rotor Stability in Turbopumps,2000, 21(3):43-45.

[8]Al-Qutub A, Khalifa A, Khulief Y. Experimental investigation of the effect of radial gap and impeller blade exit on flow-induced vibration at the blade-passing frequency in a centrifugal pump[C]. International Journal of Rotating Machinery,2009.

[9]Takayuki S, Koichi Y, Hironori H, et al. A numerical analysis of rotordynamic fluid forces on an artificial heart pump impeller in whirling motion[J]. Transactions of the Japan Society of Mechanical Engineers,2008(2): 310-316.

[10]Takayuki S, Romain P, Hironori H, et al. Measurements of rotordynamic forces on an artificial heart pump impeller[J]. Journal of Fluids Engineering, Transactions of the ASME, 2007(11): 1422-1427.

[11]Van Bokhorst E, Almasy S. Root cause analysis of vibrations and pulsations in a naphtha pipe system with centrifugal pumps [C]. Institution of Mechanical Engineers-11th European Fluid Machinery Congress,2010:169-179.

[12]蒋爱华,章艺,靳思宇,等. 离心泵流体激励力的研究：蜗壳部分[J].振动与冲击,2012,31(4):60-66.

JIANG Ai-hua,ZHANG Yi,JIN Si-yu,et al. Fluid exciting forces on centrifugual pump part Ⅰ:force on volute[J]. Journal of Vibration and Shock, 2012,31(4):60-66.

[13]蒋爱华,章艺,靳思宇,等. 离心泵叶轮流体激励力研究[J].振动与冲击,2012,31(22):123-127.

JIANG Ai-hua,ZHANG Yi,JIN Si-yu,et al. Fluid exciting forces of a centrifugual pump on impeller[J]. Journal of Vibration and Shock, 2012,31(22):123-127.