基于HHT方法的爆炸应变波时频分析

杨仁树，高祥涛，车玉龙，解北京

(1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2中国矿业大学(北京)深部岩土力学与地下工程国家重点实验室，北京 100083；3中国矿业大学(北京)资源与安全工程学院，北京 100083)

固体介质中爆炸应变波信号为瞬变的非周期、非平稳随机超动态信号。在爆源近中区，固体介质中爆炸应变波动实质为介质内质点振动总体反映。该质点振动传播的为体波，不同于通常的爆破地震波[1]，但其信号特征均属非平稳信号范畴。对固体介质中爆炸波频谱分析早期主要用傅里叶变换[2-4]。因理论发展的限制，Fourier分析方法基于线性及平稳假定。随信号分析理论与技术的发展，数据信号分析出现诸多新方法。如短时快速傅里叶变换、Cohen类、小波分析及Wagner-Ville分布等均能用于线性非平稳数据[5-7]分析，但其本质均未摆脱傅里叶分析的局限，存在基函数选择及频谱扩散问题[8]。此外，各种非线性时序分析方法被设计成非线性平稳确定性系统，但实际所得大部分信号均具有非线性非平稳特征，分析较困难。

HHT方法广泛用于地震工程[9]、机械振动信号分析[10-11]、结构损伤分析[12]等领域，能较好处理工程中非线性非平稳信号。其中对爆破振动信号HHT法的应用研究[1]取得较好效果。但用HHT方法分析研究固体介质近中区爆炸应变波信号未见报道。本文据爆炸波信号短时、瞬变、非周期、非线性、非平稳特点，用HHT方法分析爆炸应变波信号时频特征，并与STFT方法对比以证明HHT方法的优越性。为研究固体介质中爆炸应力波传播机理、工程结构的安全防护提供可靠依据。

1 HHT分析法[13]

1.1 EMD原理与算法

HHT信号分析法为全新分析技术，由EMD方法与Hilbert变换两部分组成，核心为EMD。其据信号本身的时间尺度特性，将信号分解为含有不同时间尺度且满足一定条件的一组IMF(Intrinsic Mode Function)分量。EMD算法为：① 找出信号x(t)上所有极值点，用三次样条插值函数对所有极大值点进行插值，拟合出原始信号x(t)上包络线xmax(t)。同理可得下包络线xmin(t)。上、下两条包络线含所有信号数据。按顺序连接上、下包络线均值即得一条均值线m1(t)，将原数据序列减去m1(t)可得一去掉低频的新数据序列h1(t)，用筛选过程终止准则判别不同信号h1k(t)是否IMF分量。② 符合终止准则条件的h1k(t)即为可表示信号数据中最高频成分的第一IMFc1(t)，再用x(t)减去c1(t)获得一新数据序列r1(t)。重复步骤①，获得一系列cn(t)及最后一个不可分解序列rn(t)，rn(t)代表x(t)的均值或趋势项，此时可终止模态分解过程。原始信号x(t)可由n阶IMF分量及残差rn(t)构成：

(1)

1.2 Hilbert变换与Hilbert谱

将EMD分解的每个IMF分量进行Hilbert变换，即可得每个IMF分量的瞬时频谱，综合所有IMF分量瞬时频谱可得Hilbert谱，每个IMF分量进行Hilbert变换后，将x(t)表示成Hilbert谱形式：

(2)

将式(2)三维空间中信号幅度表达为时间与瞬时频率的函数，即Hilbert谱。若振幅的平方对时间积分，可得Hilbert能量谱：

(3)

Hilbert能量谱可提供每个频率的能量计算式，表达每个频率在整个时间长度内累积的能量。对实验所测爆炸应变信号进行Matlab程序语言设计，可得HHT分析结果。

2 岩石中爆炸应变测试实验

实验中采用在水泥砂浆试件中预埋应变砖方法测试爆源近中区爆炸应变信号。水泥砂浆试块为圆柱体，尺寸Φ400 mm×450 mm；应变砖尺寸180 mm× 20 mm×10 mm。圆柱体试件与应变砖均由PC32.5普通硅酸盐水泥、黄砂(细骨料)制成，水泥砂浆配比(质量比)为水泥：黄砂：水=1∶2∶0.5。试件养护28 d后测试其物理力学参数为密度2.3 g/cm3，抗压强度56.5 MPa，弹性模量24.87 GPa，泊松比0.25，纵波速度4 445 m/s，横波速度2 080 m/s。每块模型预埋1个应变砖，埋深225 mm，理论上认为固体介质中距爆源8～150倍装药半径范围为衰减后应力波及爆生气体膨胀作用的破裂区，该区在爆破过程中占重要地位。因此在该区域内应变砖的测点布置为距炮孔4 cm、8 cm、13 cm、18 cm，每个距离处分别设置径向、横向应变片。应变片为120 Ω箔式环氧酚醛类电阻应变片，敏感栅尺寸3×2(mm)，灵敏系数2.08%。实验药包为圆柱形，装药为二硝基重氮酚(C6H2(NO2)2N2O)，装药密度ρ0=0.82 g/cm3，爆速3 991 m/s，采用桥丝贯穿装药轴心瞬时起爆。炮孔用石英砂与AB胶混合后堵塞密实。对岩土中爆炸应力波测试，选动态信号数据采集仪采样频率为40 MHz，前置放大器频率响应2.5 MHz。测试装置示意图见图1。

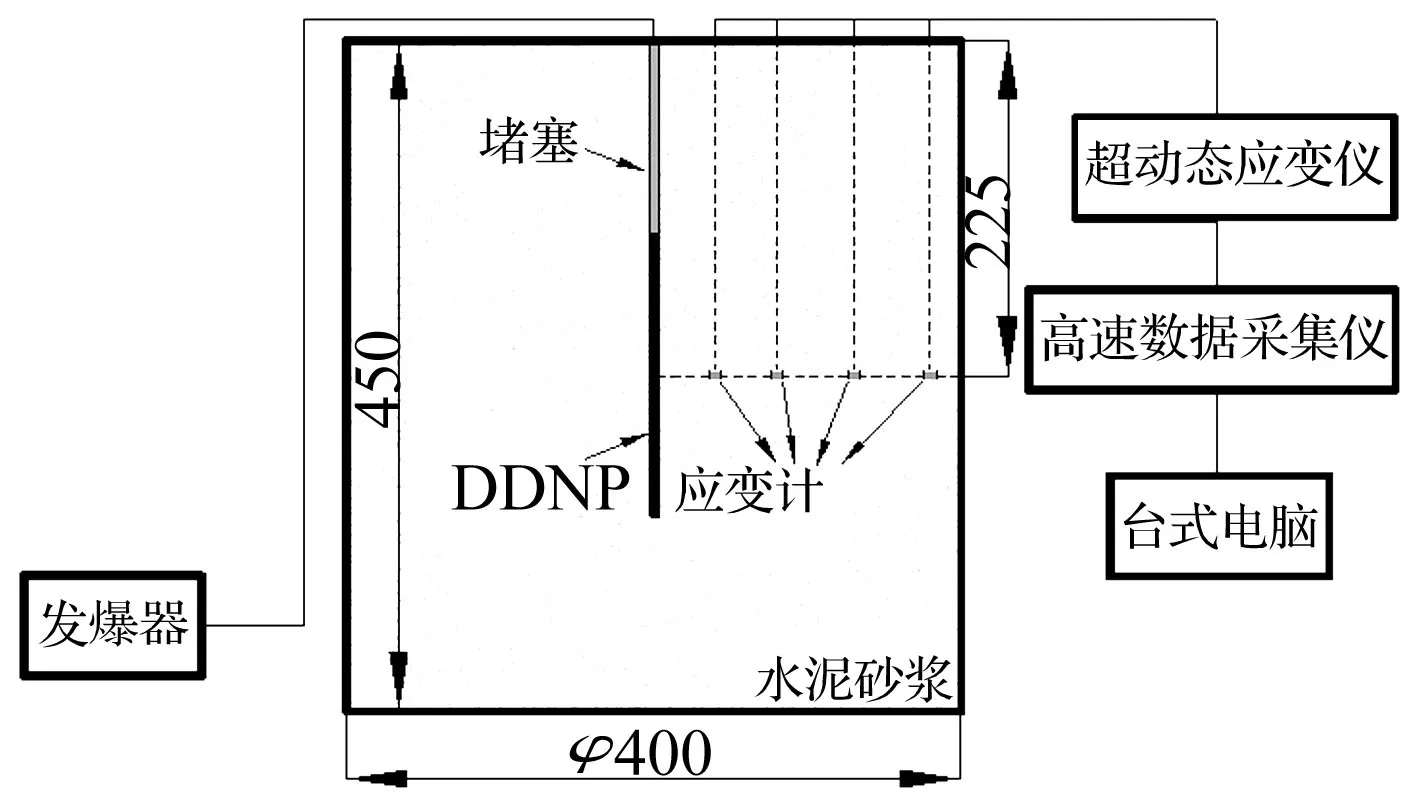
图1 测试装置示意图

3 计算结果及分析

3.1 实验结果

相同药量与起爆方式重复三组混凝土介质爆炸近中区测试实验，获得距爆源不同距离处爆炸应变波信号，限于篇幅仅以其中一组实验中同一测点处两个应变波形为例见图2，其它测点波形相似。图2中1#、2#爆炸应变波信号分别为距爆源中心4 cm处应变片所测径向应变、横向应变。由图2可见，爆炸应变波在固体近中距离处同一测点同时产生径向、横向应变，径向主要承受压应变，横向主要承受拉应变，径向应变绝对值(8×104μs)略大于横向应变绝对值(7.5×104μs)。

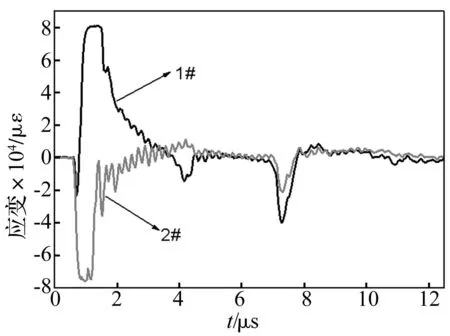
图2 所测爆炸应变信号

3.2 爆炸波信号时频特征分析

用HHT方法定量分析爆炸应变波信号的时频分布特征。对图2中1#、2#爆炸应变波信号分别进行EMD分解，并对分解的IMF分量进行快速傅里叶变换(FFT)，分析各分量频域特征，结果见图3。由图3可见，EMD分解顺序按频率由高到低进行。图3(a)、(c)中1#、2#爆炸应变波信号经EMD分解成7个IMF分量(从高频到低频)及1个残余分量R(采集信号的整体变化趋势)；图3(b)中，1#径向应变信号EMD分解出的7个IMF分量C1～C7频率范围主要集中在2.5～17.5 MHz、0～6 MHz、0～3 MHz、0～1.5 MHz、0～1 MHz、0～0.5 MHz、0～0.5 MHz；各IMF分量C1～ C7的平均频率为7.25 MHz、3.1 MHz、1.14 MHz、0.627 MHz、0.314 MHz、0.196 MHz、0.157 MHz；图3(d)中2#横向应变信号EMD分解出的7个IMF分量C1～C7频率范围主要集中在2.5～8 MHz、1～5 MHz、0～3 MHz、0～1.5 MHz、0～1 MHz、0～0.5 MHz、0～0.5 MHz；各IMF分量C1～C7平均频率为6.98 MHz、3.45 MHz、1.33 MHz、0.392 MHz、0.314 MHz、0.186 MHz、0.118 MHz。其它4组测点应变信号EMD分析结果基本相似，各测点信号IMF分量频带及相应能量分布见表1。由表1看出，或径向应变或横向应变，距爆源越近高频IMF分量频带所占能量比例越大。如1#径向IMF_C1分量(7.25 MHz)，其能量占总能量的53.6%；随爆炸应力波向远处传播，其所占能量比例大的IMF分量频带逐渐向低频率转移，如7#径向IMF_C5分量(0.275 MHz)其能量占总能量的56.2%。可见，炸药在岩石介质中爆炸的频率分布丰富，不同频率波动对介质质点做功不同。每个固有模态分量(IMF)代表1个频率段的作用结果。而爆源近中区爆炸应变波的主频率在几百千赫兹到几兆赫兹范围内。

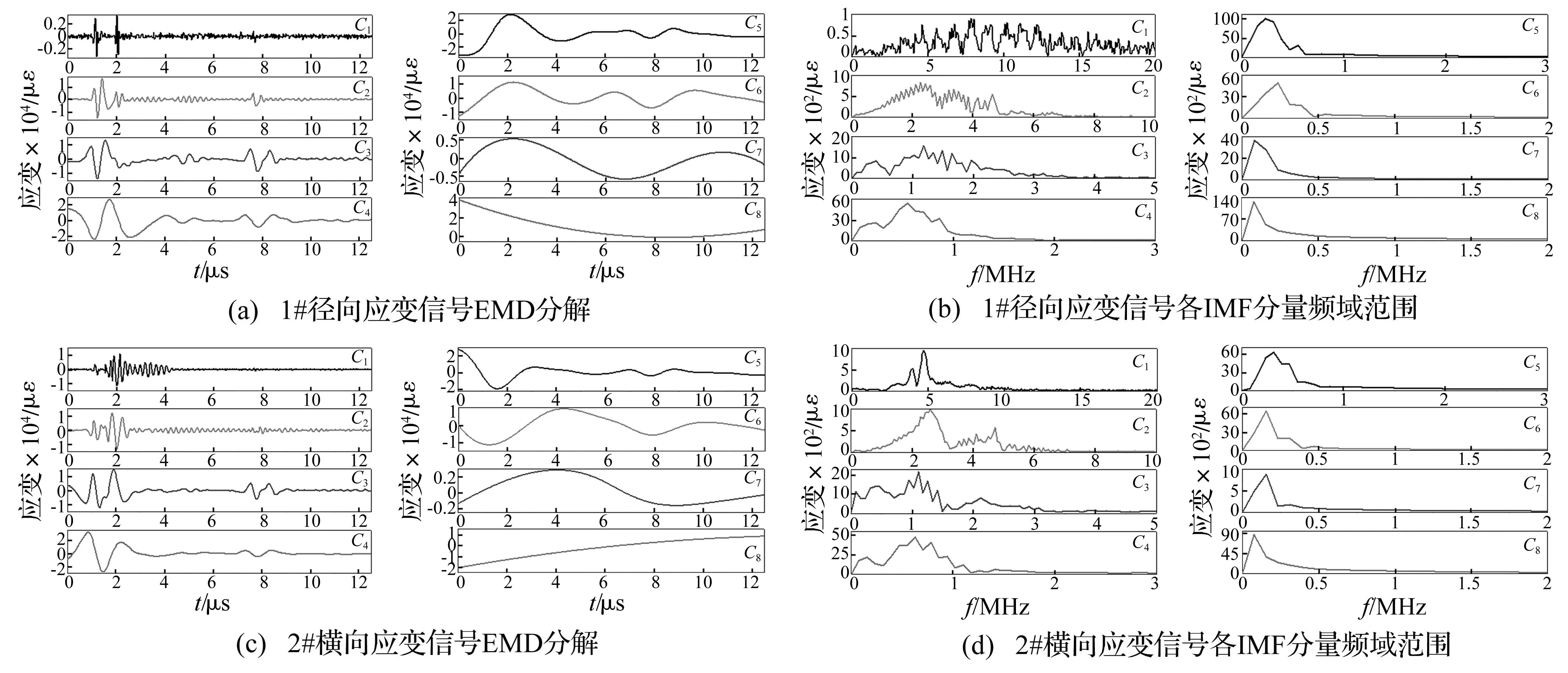
图3 爆炸应变波信号EMD分解及频域图

表1 各IMF分量所占原始信号能量百分比及频率分布

3.3 爆炸波信号HHT法与STFT对比分析

HHT方法与STFT方法与非平稳信号的优越性对比已较清楚，但对瞬变非周期非平稳随机超动态爆炸应变波信号传播细节特征，利用HHT法与STFT法对比研究岩石中爆炸应变波时频特征研究未见报道。将实测爆炸应变波信号同时用HHT法、STFT法的分析结果见图4。由图4可见，与短时傅里叶变换时频能量谱相比，希尔伯特能量谱能清晰表达能量随时间频率的分布细节，信号能量主要集中于小能量谱段，能准确刻画信号特征，而短时傅里叶变换的能量谱范围较宽，且频率分辨率较低，未体现信号本身的非平稳特性，只具有相对分布意义。此因为爆炸波传播具有多频率作用特性，短时傅里叶变换(STFT)所建频谱图为最简单、最直观的时频分布。但在分析非平稳信号时，受Heisenberg不确定性原理限制，时频分辨率不能自适应改变，时间分辨率及频率分辨率需要折中，且STFT使用固定的短时窗函数，较能降低频率分辨率，不能显示爆炸冲击信号的能量细节。而爆炸应变信号的Hilbert能量谱可清晰反映随时间频率变化的具体分布，利用HHT方法可明显表现出爆炸应变波传播细节，从而印证爆炸应变波的多频特征。

图4 爆炸应变波信号HHT变换与STFT变换比较

3.4 爆炸波信号多频率作用特性探讨

为探讨爆炸波信号多频率作用特性，分别给出空气、岩石介质中爆炸波的传播数值模拟结果及有机玻璃中不耦合装药爆炸应力波传播的动光弹实验结果。图5为爆炸波在不同介质中的传播特征。图5(a)为运用Euler-FCT格式模拟爆炸波传播。由图5(a)看出，爆炸波由不同层级压力作用于周围空气介质，产生不同幅度波动。由于爆炸波动过程的不定常性，爆炸波与周围介质作用在极短时间内往复振荡[14]。此振荡随时间、距离衰减，介质内部受冲击压缩时出现电动势、电磁辐射，必具有多频率相互作用特点。图5(b)为岩石中耦合装药爆炸应力波传播，岩土介质运用分段的Druck-Prager本构模型，模拟结果清晰表明，爆炸波动能量随时间、距离耗散，加之岩石介质的不均匀性，爆炸波会发生弥散现象，波动频率更丰富。图5(c)为有机玻璃中不耦合装药爆炸应力波动的多频段特性[15]，实验结果清晰表明，有机玻璃围绕爆源周围产生诸多疏密相间的爆炸应力波动条纹，其本质为因爆炸应力波动多频段特性作用结果。

因此，固体介质中爆炸应力波信号由各种不同频率波动共同作用，该复合叠加的波动作用于介质，若超过介质的固有频率，则介质将发生拉伸或剪切破坏。可用数值模拟及文献中数据佐证爆炸波动的多频率特性。

图5 不同介质中炸药爆炸波传播

4 结 论

爆炸应变波信号为典型的瞬变非平稳随机信号，且爆炸应力波频谱构成复杂、影响因素众多。HHT变换能较好用于具有非线性、非平稳特性的爆炸应变波信号分析中，且能提取时程曲线的主要特征信息，结论如下：

(1) 通过爆炸应变波信号的EMD分解及时频分析知，爆源近中区爆炸应变波的主频率在几百千赫兹到几兆赫兹范围内。

(2) 通过爆炸波信号HHT法与STFT时频能对比分析知，Hilbert能量谱能较好、清晰描述爆炸应变波信号能量在时频谱的分布，可获得爆炸应变波信号的频谱及功率谱随时间变化的细节特征。

(3) 通过分析爆炸波在空气、岩石介质中传播数值模拟、爆炸应变波在有机玻璃介质传播动光弹实验结果知，爆炸波信号具有多频率作用特性，即介质中爆炸波信号波形为由不同频率波动共同作用结果。

[1]张义平，李夕兵，左宇军.爆破震动信号的HHT分析与应用[M]. 北京：冶金工业出版社，2008.

[2]宋熙太，任建民.爆炸波分析及其波谱[J].爆炸与冲击，1982,4:33-42.

SONG Xi-tai, REN Jian-min. Analysis of explosion waves and wave spectrum[J]. Explosion and Shock Waves, 1982, 4: 33-42.

[3]李廷芥，洪悯萱.瞬态波形的频谱分析及在岩石动力学中的应用[J]. 爆炸与冲击, 1985,5(4):10-16.

LI Ting-jie, HONG Min-xuan. Spectral analysis of transient waveforms and its applications in rock dynamics[J]. Explosion and Shock Waves, 1985,5(4):10-16.

[4]洪悯萱,李廷芥.爆炸波的频谱分析[J].岩土力学,1987,8(1): 51-57.

HONG Min-xuan, LI Ting-jie. Spectral analysis of blast waveforms[J]. Rock and Soil Mechanics, 1987,8(1)：51-57.

[5]赵建平, 陈寿如.基于短时Fourier变换的爆炸波时频能分布及分离[J]. 采矿技术,2011, 11(5): 84-86.

ZHAO Jian-ping, CHEN Shou-ru. Blast wave time-frequency energy distribution based on STFT[J]. Mining Technology, 2011, 11(5): 84-86.

[6]毛婧，韩焱.小波分析在爆炸冲击波信号处理中的应用[J].弹箭与制导学报,2007,27(4):137-144.

MAO Jing, HAN Yan. Wavelet analysis in explosive shock wave signal processing[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007,27(4):137-144.

[7]赵建平,林杭.基于时频能分析技术的爆炸波能量分布及分离[J].岩石力学与工程学报,2012, 31(S1): 3278-3285.

ZHAO Jian-ping, LIN Hang. Energy distribution and separation of blast wave based on time-frequency energy analysis technology[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S1): 3278-3285.

[8]赵杨，武岳，曹曙阳，等. 利用HHT方法对非平稳风力的时频分析[J]. 振动与冲击, 2011, 30(2): 5-14.

ZHAO Yang, WU Yue, CAO Shu-yang,et al. Time-frequency analysis of a non-stationary wind pressure with HHT method[J]. Journal of Vibration and Shock, 2011, 30(2): 5-14.

[9]胡灿阳，陈清军. 基于HHT法的地震地面运动局部谱密度估计[J]. 振动与冲击，2007,26(10):126-131.

HU Can-yang, CHEN Qing-jun. Estimation of local spectral density of earthquake ground motion based on HHT theory[J]. Journal of Vibration and Shock, 2007,26(10):126-131.

[10]张帅，杨勇，韩清凯，等. 基于HHT的转子系统定点碰摩实验研究[J]. 振动与冲击，2010,29(7)：121-125.

ZHANG Shuai, YANG Yong, HAN Qing-kai,et al. Experimental study on a rotor system with rub-impact at fixed limiter based on HHT[J]. Journal of Vibration and Shock, 2010,29(7)：121-125.

[11]唐先广，郭瑜，丁彦春. 基于独立分量分析与希尔伯特-黄变换的轴承故障特征提取[J]. 振动与冲击,2011, 30(10):45-49.

TANG Xian-guang, GUO Yu, DING Yan-chun. Rolling element bearing fault feature extraction based on HHT and independent compoment analysis[J]. Journal of Vibration and Shock, 2011,30(10):45-49.

[12]黄天立.结构系统和损伤识别的若干方法研究[D].上海：同济大学，2007.

[13]Huang N E, Shen S S P. The Hilbert-Huang transform and its applications[M]. World Scientific Publishing Co. Pte. Ltd., Toh Tuck Link, Singapore,2005.

[14]奥尔连科JI II,著. 孙承纬,译.爆炸物理学[M].北京：科学出版社,2011.

[15]曹跃，赵泉，孔安.不耦合装药爆炸扩腔机理研究[J].爆破,2005,22(3):21-25.

CAO Yue, ZHAO Quan, KONG An. The springing mechanism of spherical charges in an eccentric decouple pattern[J]. Blasting, 2005,22(3):21-25.