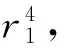自同构群阶为8p1p2...pr的有限幂零群*

钟祥贵,蒋青芝,吴 勇,张小芳

(广西师范大学数学科学学院,广西 桂林 541004)

自同构群阶为8p1p2...pr的有限幂零群*

钟祥贵,蒋青芝,吴 勇,张小芳

(广西师范大学数学科学学院,广西 桂林 541004)

给出自同构群阶为8p1p2...pr(p1,p2,...,pr是不同的奇素数)的有限幂零群的完全分类.

自同构群;幂零群;群阶;有限群

对于给定的自然数n,解自同构群方程|Aut(G)|=n的问题,学者们[1-9]作了很多研究.文献[1]证明了对任意给定的奇素数p,不存在有限群G满足|Aut(G)|=p5.文献[2-3]对自同构群阶为8pq,8p2q2(p,q为不同的奇素数)的有限幂零群作了研究.文献[4]对自同构群阶为16p(p为奇素数)的有限幂零群作了研究.文献[5]对自同构群阶为16p2(p为奇素数)的有限交换群作了研究.笔者的目的是继续这方面的研究,作为文献[3]的进一步扩展,讨论自同构群方程|Aut(G)|=8p1p2...pr(p1

1 相关引理

引理1[6]设P为非循环p群,|P|>p2.若|P/Z(P)|≤p4,则|P|整除|Aut(P)|.

引理2[7]不存在有限群G使得|Aut(G)|=n,其中n是4次方自由的奇数.

引理3[8]八阶非循环群P有以下4种互不同构的类型：Z2×Z2×Z2,Z4×Z2,四元数群Q8,二面体群D8.并且|Aut(P)|依次为23·3·7,23,23·3,23.

引理4[8]设Q为q-群(q为素数).如果|Aut(Q)|=m,那么:

(1)m=1时,Q≅Z2;

(2)m=2时,Q≅Z3,Z4;

(3)m=4时,Q≅Z5,Z8;

(4)m=8时,Q≅Z2×Z4,D8,Z16.

引理5[9]设L为奇阶有限幂零群,那么|Aut(L)|=4p1p2...pr(pr是最大素因子)当且仅当L同构于下列群之一:

(1)L1=Zp,其中p=4p1p2...pr+1为素数;

(2)L2=Z(4p1p2...pr+1)2,其中4p1p2...pr-1+1=pr;

(3)L3=Zp×Zq,其中p,q为互异素数,p-1,q-1为无平方因子的偶数;

(4)L4=Zp×Zq2,其中p,q为互异素数,p-1,q-1为无平方因子的偶数;

(5)L5=Zp2×Zq2,而p,q为互异素数,p-1,q-1为无平方因子的偶数.

2 定理及其证明

定理1 设p1

(1)Z2×Z2×Li,i=1,2,3,4,5,其中L1=Zp且p=4p2...pr+1为素数,L2=Z(4p2...pr+1)2且pr=4p2...pr-1+1,L3,L4,L5的结构如同引理5所述;

(2)Z2×Z2×Z2,Q8;

(1) 若|R1|=4,则R1是四阶初等交换群,此时Aut(R1)的阶为2·3,从而p1=3,并且3

(ⅰ)L1=Zp,其中p=4p2...pr+1为素数;

(ⅱ)L2=Z(4p2...pr+1)2,其中4p2...pr-1+1=pr;

(ⅲ)L3=Zp×Zq,p,q为大于3的互异素数,p-1,q-1为无平方因子的偶数;

(ⅳ)L4=Zp×Zq2,p,q为大于3的互异素数,p-1,q-1为无平方因子的偶数;

(ⅴ)L5=Zp2×Zq2,p,q为大于3的互异素数,p-1,q-1为无平方因子的偶数.

(2) 若|R1|=8,则R1为引理3给出的非循环群,其自同构群阶分别为23·3·7,23,23·3,23.如果r≥2,那么|Aut(R2×...×Rk)|=p2...pr.这时由引理2知R2×...×Rk不存在.从而G同构于Z2×Z2×Z2,或者四元数群Q8.

情况1t=1.由文献[1]的结论可知，2整除|Aut(Ri)|(i=1,...,s-1).注意到|Aut(Ri)|整除8p1p2...pr,所以2≤s≤4.下面就s的值分别进行讨论.

情况2t=2.注意到|Aut(Ri)|整除4p1p2...pr,2≤s≤3.下面就s的值分别进行讨论.

[1] CURRAN M J.Automorphisms of Certainp-Groups (pOdd)[J].Bulletin of the Australian Mathematical Society,1988,38(2):299-305.

[2] MENG Wei,LU Jiakuan,CHEN Kelin.Finite Nilpotent Groups with Automorphism Group of Order 8p2q2[J].South Asian J. Math.,2011,1(1)：29-33.

[3] 孟 伟,李春琴.具有8pq阶自同构群的有限幂零群[J].云南民族大学学报：自然科学版,2011,20(4):272-274.

[4] 钟祥贵,张福生,张 洪.自同构群阶为16p的有限幂零群[J].广西师范大学学报：自然科学版,2009(1):21-24.

[5] 王秀花. |A(G)| = 24p2(p为奇素数) 的有限Abel 群[J].湖北民族学院学报：自然科学版,2007,25(4):125-128.

[6] DAVITT R M.On the Automorphism Group of a Finitep-Group with a Sma1l Central Quotient[J].Canadian Journal of Mathematics,1980,32:1 168-1 176.

[7] 钱国华.某些有限群的自同构群[J].中国科学,2003,33(1):75-82.

[8] 张远达.有限群构造[M].北京:科学出版社,1982.

[9] 夏巧珍,陈贵云,曹洪平.自同构群阶为4p1p2...pn的有限群[J].中国科学,2012,42(6):611-617.

(责任编辑 向阳洁)

FiniteNilpotentGroupswiththeAutomorphismGroupofOrder8p1p2...pr

ZHONG Xianggui,JIANG Qingzhi,WU Yong,ZHANG Xiaofang

(College of Mathematical Science,Guangxi Normal University,Guilin 541004,Guangxi China)

In this paper,the finite nilpotent groups with the automorphism group of order 8p1p2...pr(p1,p2,...,prare distinct odd prime numbers) are classified.

automorphisms group;nilpotent group;group order;finite group

1007-2985(2014)01-0001-03

2013-04-19

国家自然科学基金资助项目(11261007)；广西研究生教育创新计划项目(YCSZ2012051)

钟祥贵(1963-),男,湖南武冈人,广西师范大学数学科学学院教授,主要从事有限群论研究.

O152.1

A

10.3969/j.issn.1007-2985.2014.01.001