一类次线性Hamilton系统的周期解*

张申贵

(西北民族大学数学与计算机科学学院,甘肃 兰州 730030)

一类次线性Hamilton系统的周期解*

张申贵

(西北民族大学数学与计算机科学学院,甘肃 兰州 730030)

Hamilton系统是一类比较重要的微分方程模型.利用临界点理论中的鞍点定理研究非自治Hamilton系统周期解的存在性.在具有次线性增长非线性项时,给出了相关周期解存在的充分条件,推广了Ahmad-Lazer-Paul型强制性条件.

非自治Hamiltonian系统;次线性增长非线性项;周期解;临界点

Hamilton系统广泛存在于数理科学、生命科学以及社会科学的整个领域,特别是天体力学、等离子物理、航天科学以及生物工程中的很多模型都以Hamilton系统(或它的扰动系统)的形式出现,因此对该系统的研究具有重要的理论和实际意义.非自治Hamilton系统周期解的存在性一直是人们所关注的重要问题[1-6].

1 问题的提出

考虑非自治Hamilton系统

(1)

文献[2]中假设存在正常数M1,M2及0≤α<1,使得

|H(t,u)|≤M1|u|α+M2,

(2)

且H满足Ahmad-Lazer-Paul型强制性条件

(3)

成立时,得到了非自治Hamiltonian系统周期解的存在性.

文献[3]在H满足(2),(3)式时,研究了系统(1)多重周期解的存在性.

定理1 设H满足(2)式,且假设H满足

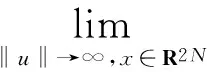
(4)

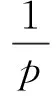
注1 (2)式表明非线性项H(t,u)是次线性增长的.(3)式推广了Ahmad-Lazer-Paul型强制性条件,易见在(3)式中极限可以是下方有界的,极限值放宽为].

定理2 设H满足(2)式,且假设H满足

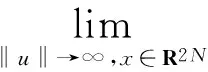
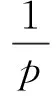
2 预备知识

u,v

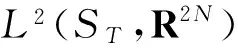
‖u‖L2≤C‖u‖ ∀u∈X.

(5)

令{e1,e2,...,e2N}是R2N中的典范基,对于j∈Z,

X(j)=span{sin(jt)el-cos(jt)el+N,cos(jt)el+sin(jt)el+N|1≤l≤N}，

在X上定义泛函φ为

则φ是连续可微的,且

φ′(u),v=(-J,v)dt-(H(t,u),v)dt=(u+-u-,v)-

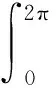
从而u是问题(1)的解当且仅当u是φ的临界点.

定义1 设X为Banach空间,若对任何点列{un}⊂X,由{φ(un)}有界,φ′(un)→0,可推得{un}有收敛子列,则称泛函φ∈C1(X,R)满足(PS)条件.

(ⅰ) 存在e∈Bρ∩E1和常数ω>σ,使得φ|e+E2≥ω.

(ⅱ) 存在常数σ和ρ,使得φ|∂Bρ∩E1≤σ.

3 定理的证明

定理1的证明利用引理4来证明定理1.下面用c表示常量.

第1步证明(PS)条件成立.即指对任何点列{un}⊂X,由{φ(un)}有界,φ′(un)→0(n→∞),可推得{un}有收敛子列.下面证明(PS)条件成立,先证{un}在X中有界.

对∀u∈X,有u=u-+u0+u+,其中u-∈X-,u0∈X0,u+∈X+.设{un}⊂X,使得

|φ(un)|≤c,φ′(un)→0n→∞.

(6)

由(6)式,有

φ′(u),φ=(-J,φ)dt-(H(t,u),φ)dt=o(‖φ‖) ∀φ∈X.

(7)

(8)

由(7),(8)式,有

(9)

同理可证

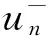
(10)

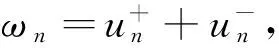
(11)

由(11)式,并注意到0≤α<1,有

(12)

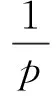
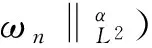
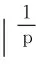
(13)

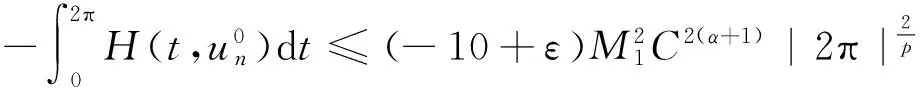
(14)

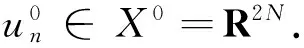
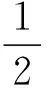
反设{un}在X中有无界,当n→∞时,‖un‖→∞.

由ε的任意性,由(12)式,当n→∞时,φ(un)→-∞,这与(6)式矛盾.故{un}在X中有界,由标准讨论知φ满足(PS)条件.

第2步根据引理4,要证明定理1,仅需证明下面事实:

(ⅱ) 当‖u‖→+∞时,φ(u)→-∞，对u∈X-⊕X0成立.

先证(ⅰ)成立.由(2),(5)式,对u∈X+,有

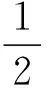
由0≤α<1,当‖u‖→∞时,有φ(u)→+∞,从而条件(ⅰ)成立.

(15)

由(14),(15)式,有

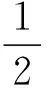
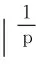
令ε充分小,由0<α<1,当‖u‖→∞时,有φ(u)→-∞,从而条件(ⅱ)成立.

定理2的证明方法与定理1类似,文中不再给出证明.

[1] DAOUAS ADEL,TIMOUMI MOHSEN.Multiple Periodic Solutions of Nonautomous Hamiltonian Systems[J].Arch. Math.,2002,79:131-140.

[2] HAN Zhiqing.Existence of Periodic Solutions of Linear Hamiltonian Systems with Sublinear Perturbation[J].Boundary Value Probiems,2010(12):123-131.

[3] TIMOUMI MOHSEN.Multiple Periodic Solutions for Some Class of First-Order Hamiltonian System[J].Applied Mathematics,2011(2):846-853.

[4] LUAN Shixia,MAO Anmin.Periodic Solutions of a Class of Nin-Autonomous Hamiltonian Systems[J].Nonlinear Analysis,2005,61:1 413-1 426.

[5] FEI Guihua.On Periodic Solutions of Superquadratic Hamiltonian Systems[J].Electron J. Diffence Equation,2002(8):1-12.

[6] MAWHIN J,WILLEM M.Critical Point Theory and Hamiltonian Systems[M].New York:Springer Verlag,1989.

(责任编辑 向阳洁)

PeriodicSolutionofaClassofSublinearHamiltonianSystem

ZHANG Shengui

(College of Mathematics and Computer Science,Northwest University for Nationalities,Lanzhou 730030,China)

Hamiltonian System is an important model of differential equation.In this paper,the author investigates the existence of periodic solution for nonautonmous Hamiltonian System with sublinear nonlinearity by saddle point theorem in critical point theory.Some sufficient conditions for the existence of periodic solutions are obtained,and the results improve the Ahmad-Lazer-Paul’s coercive condition.

nonautonmous Hamiltonian system;sublinear nonlinearity;periodic solution;critical point

1007-2985(2014)01-004-04

2013-04-24

国家自然科学基金资助项目(31260098)；西北民族大学中青年科研项目(12XB38)

张申贵(1980-)，男,甘肃兰州人,西北民族大学数学与计算机科学学院副教授,主要从事非线性泛函分析研究.

O175.12

A

10.3969/j.issn.1007-2985.2014.01.002