串联随进弹对预开孔跑道的斜侵彻研究

李 强， 姜春兰， 毛 亮

(1.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081; 2. 中国人民解放军96531部队，北京 102202)

现代战争中对制空权的掌握是取得胜利的重要保证，而控制或摧毁敌方机场跑道则成为遏制敌制空权直接有效的手段。目前串联复合战斗部是毁伤机场跑道最有效的战斗部形式之一。串联战斗部通过一级聚能装药战斗部对跑道开孔，后级随进爆破战斗部沿孔道通过瞬时加速随进到跑道内部爆炸，实现对机场跑道的毁伤。

由于二级随进战斗部对跑道的毁伤效能主要取决于随进弹最终的起爆姿态和炸点深度，因此研究混凝土介质对随进弹的随进姿态和侵彻深度的影响规律有着重要意义。本文通过预开孔方式来模拟前级战斗部对跑道的开孔效果，预先赋予随进弹初始速度，采用LS-DYNA软件对侵彻过程进行三维数值仿真，得到随进弹在不同随进速度，不同攻角及不同介质界面条件下随进姿态和侵彻深度的规律，并进行了理论分析和实验验证，为选取合适的炸点深度和起爆姿态提供依据。

1 随进弹侵彻机场跑道理论分析

当弹丸撞击混凝土介质时，在弹丸前的介质由于受到很大的冲击力，其颗粒间的联系被破坏，与此同时压缩邻近介质，产生侵彻阻力。以尖头弹为例，影响其侵彻阻力的主要因素是弹丸的侵彻速度、攻角以及界面介质的性质。图1所示为弹丸侵彻阻力示意图。

图1 弹丸侵彻阻力示意图

在通常情况下，侵彻阻力可以写成如下的表达形式[1]：

F=c1+c2v+c3v2

(1)

这里对攻角δ0作如下规定：顺着弹道前进的方向，当弹尖位于弹道的左边，则δ0为负；反之为正。在有攻角的情况下，法向阻力可表达为：

(2)

其中,b1为攻角零时的正面阻力，b2为攻角为90°时的正面阻力。

由(2)式可得FN随sin2δ0成正比例增加，若设定弹丸向右斜侵彻，则当攻角在0°～90°范围内变化时，sin2δ0为正值，弹道沿逆时针弯曲；攻角在-90°～0°时，sin2δ0为负值，弹道沿顺时针弯曲。图2为攻角及对弹道影响示意图。

2 数值模拟

2.1 有限元模型及算法选择

随进弹对多层介质侵彻过程是一个多物质相互接触作用，大范围靶体单元中局部物质迅速变形失效的过程[2]，仿真中采用Lagrange计算方法可以准确描述。

图3 跑道网格模型图

图3为预开孔机场跑道网格模型，图4为跑道实体模型，上层混凝土面层厚400 mm，压实碎石层厚300 mm，粘土层厚300 mm[3]。假设一级战斗部将第一层混凝土沿全弹落角方向(随进弹随进速度方向)完全击穿，并且口径大于随进弹弹径。中下两层跑道网格采用中心密边缘疏的形式[4]，弹丸及跑道均采用 1/2模型。在靶板模型四周和最底层设置透射边界不允许应力波反射来模拟较大范围靶体。随进弹弹径130 mm，弹长170 mm，壳体厚4.5 mm。

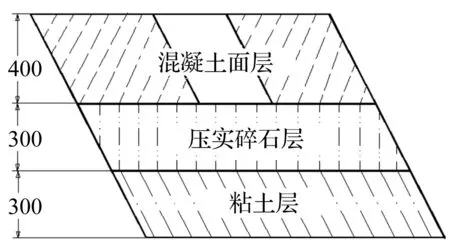
图4 跑道实体模型图

2.2 材料模型及计算参数

选用HJC模型作为混凝土面层和压实碎石层的材料动态模型。HJC模型是专门为描述脆性材料在冲击载荷下的动态力学性质而开发的材料模型，考虑了大应变、高应变率和高压情况，同时结合损伤理论考虑了材料的拉伸脆断行为，能较好反应混凝土和碎石层的力学特性。

HJC模型的屈服面等效应力定义为[5]：

(3)

式中,A为无量纲粘性常数，B为压力强化系数，N为压力硬化系数。c为应变率系数。ε*为无量纲应变率，P*为无量纲压力，D为损伤度。

粘土层采用Soil-and-Foam材料模型，可以较真实地反应出粘土层受随进弹的作用过程。该模型的理想塑性屈服函数Φ可定义为：

φ=J2-[a0+a1p+a2p2]

(4)

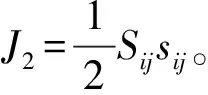
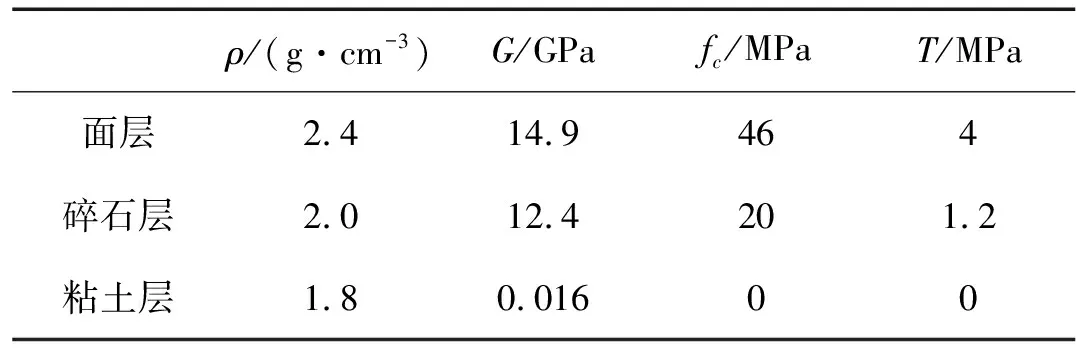
表1 跑道材料模型参数

随进弹壳体采用Johnson-Cook模型，其流动应力可定义为[6]

(5)

其中ε为等效塑性应变，A,B,c,m,n为常数，T*为无量纲温度，ε*为等效塑性应变率。其具体参数及计算公式可见文献[6]，弹体内的装药用相同密度的惰性材料代替，采用弹塑性模型。表2为随进弹材料模型参数。

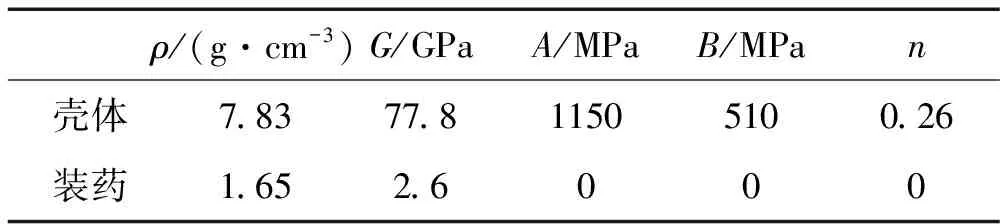
表2 随进弹材料模型参数

2.3 仿真计算及分析

2.3.1 随进速度对侵彻规律的影响

由于预开孔假设一级战斗部将第一层混凝土完全击穿，因此先研究弹丸在侵彻碎石层时随进速度对侵彻规律的影响。设定弹体在接触靶板前，以落角60°向右随进，攻角均为0，对随进速度V分别选取100 m/s，150 m/s，200 m/s,350 m/s的随进弹在碎石层介质中进行了仿真模拟，所得结果如图5所示，随进深度h(弹尖到跑道表面的垂直距离)和偏转角度θ(弹丸终止时轴线与较随进前弹轴偏转的角度，正为逆时针，负为顺时针)如表3所示。

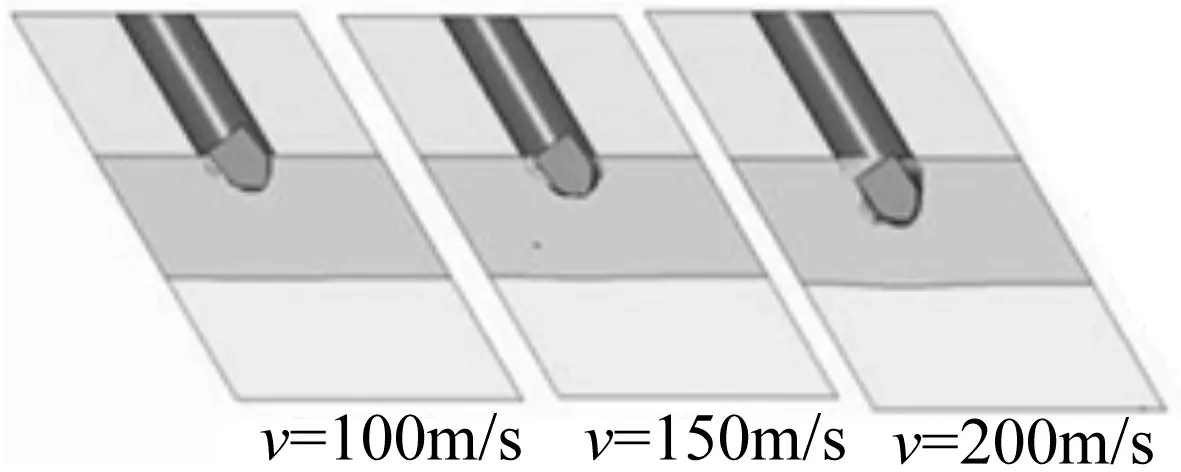
图5 不同随进速度侵彻结果

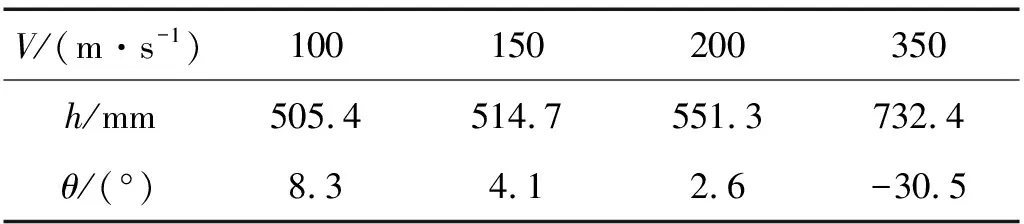
表3 不同随进速度侵彻数据

可以看出，随着随进速度增大，随进深度逐渐增加。由于随进弹的炸点深度对爆炸毁伤效果具有重要影响，过浅则不能有效毁伤，过深会在跑道地下爆炸形成隐坑，也不能对跑道形成有效毁伤[7]。文献[7]通过实验论证提出当炸点深度在3.4～4.2倍装药口径，即560 mm左右时可以获得较理想毁伤效果，结合本文仿真结果可得出推论随进速度控制在200 m/s左右比较适宜。

由表3可得出当随进弹只在碎石层中侵彻时，随进速度越低，随进弹在侵彻过程中弹体姿态越易发生偏转。当速度V=350 m/s时弹丸已侵入粘土层，通过不同介质界面使得弹丸发生较大偏转，这点将在2.3.3详细阐述。

2.3.2 随进攻角对侵彻规律的影响

随进侵彻弹如果在初始加速时受到不均匀扰动，会使随进速度方向与弹轴不重合而产生攻角。为了排除跑道介质对弹体随进姿态的影响，选用2.3.1研究中弹体未发生明显偏转的随进速度，即200 m/s，对13组不同攻角取值的随进弹在碎石层中的随进过程进行了数值模拟。图6为攻角取0，±5°和±10°时随进弹侵彻结果对比图。表4为不同攻角取值下的随进弹侵深和偏转角度数据，图7为弹体偏转角度及侵彻深度随攻角变化规律。

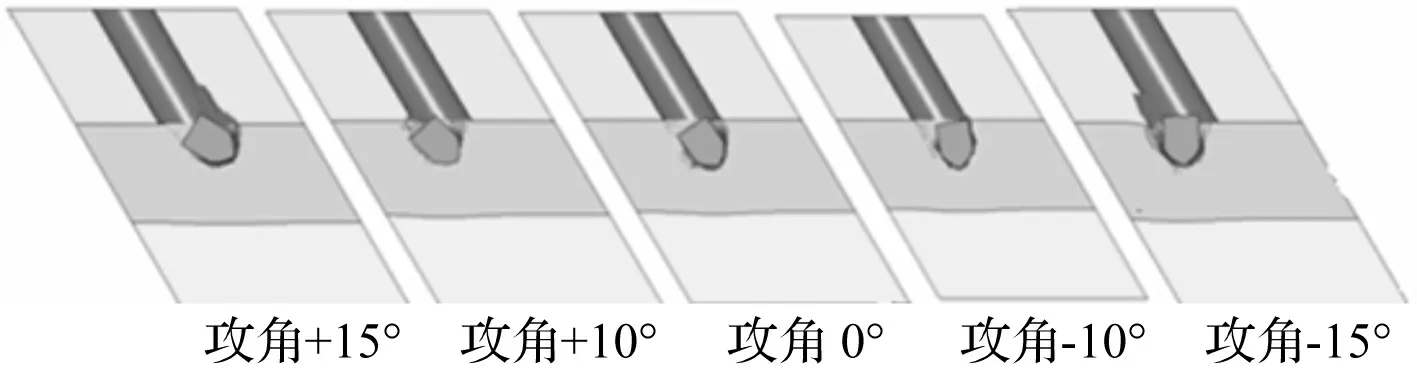
图6 不同攻角侵彻结果图

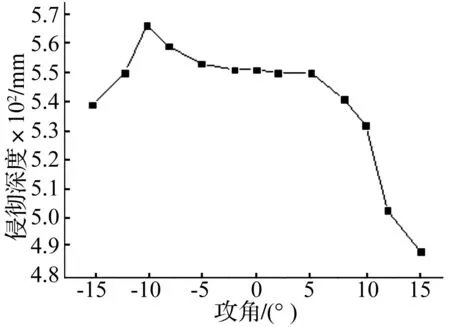
图7 侵彻深度随攻角变化规律

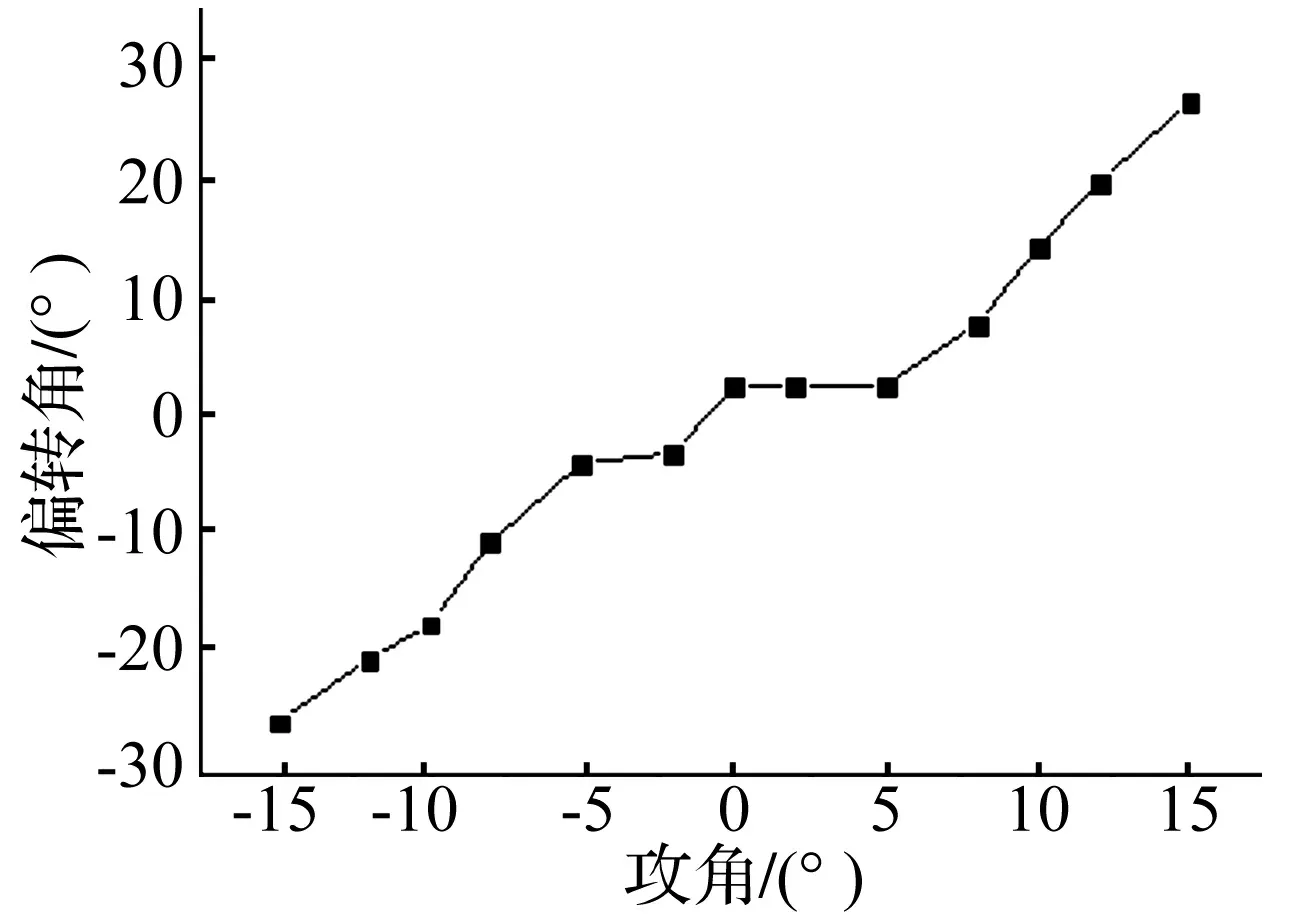
图8 偏转角随攻角变化规律

可以看出随进弹在随进速度均为200 m/s的情况下，不同攻角取值会使弹体姿态发生不同程度和方向的偏转。由图6和图7可知，攻角为负值时弹体沿顺时针方向偏转；无攻角弹体基本未发生偏转；攻角为正值时弹体沿逆时针方向偏转；攻角值越大，偏转的程度也越大。以上结论与理论分析中由式(2)得出的结论一致。从上可得出一个规律，即弹体偏转方向总是与攻角方向保持一致。

由图8可知攻角在-5°～+5°范围内，攻角变化对随进弹侵深和姿态均影响不大。随着正攻角取值增大，弹体趋向于以半平躺的姿态结束侵彻，侵彻深度逐渐降低，但以该姿态起爆有利于爆轰波的纵向传播，增大混凝土面层隆起破坏效应。随着负攻角取值增大，弹体趋向以垂直姿态结束侵彻，该姿态下爆轰波易于横向扩散，有助于增大毁伤体积，但对表面隆起破坏效果较差。当攻角为-10°时，侵彻深度达到最大值，说明存在一个最佳攻角使侵彻深度最大。综上可见不同攻角取值对随进弹侵爆效果有较大影响，在串联弹的设计中，可以根据战术的需要人为地控制攻角的取值范围，以实现指标的最优化。

2.3.3 介质界面对侵彻规律的影响

为研究不同介质界面对随进弹姿态的影响，随进弹选取可以穿透碎石层到达粘土层的随进速度。图9为随进弹在落角60°，攻角为0，V= 350 m/s时通过相同材料介质层面和不同材料介质层面时的侵彻姿态对比图，图9(a)混凝土中层与下层同为碎石层，图9(b)中层为碎石层，下层为软介质粘土层。

图9 随进弹通过相同介质和不同介质姿态对比图

可观察到图9(a)弹头侵入下层混凝土一小部分，但未发生明显偏转，图9(b)侵彻深度更深，且弹头发生严重偏转。这是由于随进弹前端进入粘土层后尾段还在碎石层中，两种介质的侵彻阻力不同，随进弹头部和尾部受到的翻转力相加后的合力要大于在单一介质中侵彻的合力，所以弹尾瞬时阻力大于弹头阻力，产生了一个顺时针方向的翻转力矩，导致弹体姿态发生了顺时针的偏转。通过该仿真可以分析出随进弹在从硬介质向软介质通过时，介质界面加速了随进弹的偏转作用。

3 实验验证

为对以上有限元仿真结果进行验证，更准确地把握侵彻规律，进行了对混凝土的斜侵彻静爆实验。实验中将串联战斗部(一级为聚能战斗部，二级为细砂填充的无装药随进弹，中间有隔爆装置)置于倾斜铁架的滑槽中，与水平地面呈60°，运用电起爆装置给出点火信号，通过自制发动机对随进弹进行加速的方式来控制随进弹的侵彻速度。一级聚能战斗部可以保证跑道混凝土面层被击穿且直径大于随进弹直径。共打四发实验弹，1,2号弹随进速度为200m/s左右，3,4号弹随进速度为350m/s左右，四发弹均控制攻角约为0。得到的实验结果如图10所示。

图10 实弹开坑侵彻效果

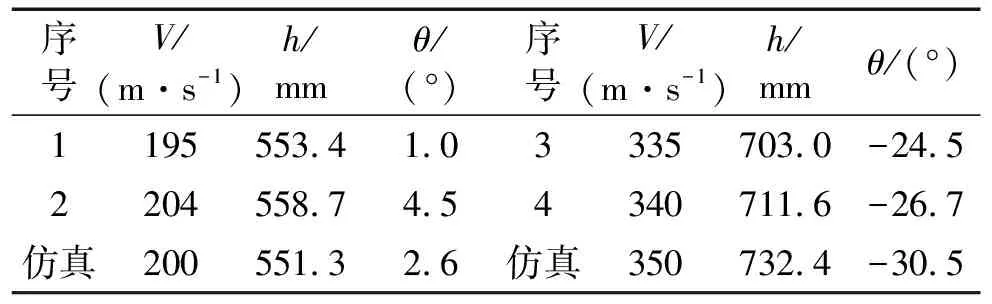
表4 实验与仿真数据对比

可以看出四发实验弹开孔均大于随进弹直径，且深度均穿透第一层400 mm混凝土，与仿真所设定的前提条件相符。表4为四发实验弹与仿真结果的数据对比，h为最大侵彻深度，θ为弹体终止侵彻时的偏转角。由表4可知随进弹在两种随进速度下对跑道的侵彻深度和弹体偏转角的实验结果与数值仿真结果相吻合，验证了仿真模型和参数选取的合理性。

4 结 论

根据随进弹随进速度，介质界面以及攻角的不同，对预开孔跑道斜侵彻过程进行了数值模拟仿真和实验验证，可得到以下结论：

(1)随着随进速度增大，随进深度也逐渐增加，当随进弹的侵彻速度满足侵入粘土层后侵深增加十分明显。随进速度越低，随进弹在侵彻过程中弹姿态越容易发生偏转。按照炸点深度理论推论随进速度控制在200m/s左右比较适宜。

(2)攻角在-5°～+5°范围内，攻角变化对随进弹侵深和姿态均影响不大，随着攻角值越大，偏转的程度也越大。攻角为负值时弹体沿顺时针方向偏转；无攻角弹体基本未发生偏转；攻角为正值时弹体沿逆时针方向偏转；即弹体偏转方向总是与攻角方向保持一致。可以考虑根据战术的需要人为地控制攻角的取值范围，以实现指标的最优化。

(3)随进弹在从硬介质向软介质侵彻时，介质界面加速了侵彻弹的偏转作用。

参 考 文 献

[1]华 恭，欧林尔.弹丸作用和设计理论[M].北京：国防工业出版社，1976:19-29.

[2]曾必强，姜春兰，王在成.反跑道动能弹斜侵彻机场多层跑道的三维数值模拟[J].兵工学报，2008，28(12):1433-1437.

ZENG Bi-qiang, JIANG Chun-lan, WANG Zai-cheng. 3D Numerical simulation of oblique penetration of antirunway penetrator to a multilayer runway target[J]. Journal of China Ordnance, 2008, 28(12):1433-1437.

[3]姜春兰，邢郁丽，王在成,等. 串联反跑道子弹药随进级结构参数优化[J].北京理工大学学报，2000,20(5):647-650.

JIANG Chun-lan, XING Yu-li, WANG Zai-cheng, et al. Optimizing structure parameters of following bomb of tandem anti-runway submunition[J]. Transactions of Beijing Institute of Technology, 2000, 20(5):647-650.

[4]杨冬梅,王晓鸣.反机场弹药斜侵彻多层介质靶的三维数值仿真[J].弹道学报,2004,16(3):83-87.

YANG Dong-mei，WANG Xiao-ming. 3D-numerical simulation of anti-runway bomb penetrating multilayer medium[J]. Journal of Ballistics，2004，16 (3):83-87.

[5]朱 剑，汪文革，王鹏华.无控子弹侵彻机场跑道数值仿真[J].弹箭与制导学报，2011 31(1):103-106.

ZHU Jian, WANG Wen-ge, WANG Peng-hua. The numerical simulation about penetration effect of unguided ammunition to airfield runway[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2001, 31(1):103-106.

[6]LSTC. LS-DYNA Keyword User’s Manual [M]. California:LSTC, 2003.

[7]王在成. 串联装药对机场跑道毁伤效应研究[D].北京：北京理工大学，2012.