提升小波包最优基分解算法在爆破振动信号分析中的应用研究

路 亮, 龙 源, 谢全民,3, 刘好全, 赵长啸,3, 李兴华

(1.解放军理工大学 野战工程学院，南京 210007;2.中国人民解放军72351部队，山东 莱芜 271109；3.武汉军械士官学校 弹药修理与销毁教研室，武汉 430075)

随着工程爆破技术在市政工程中的大力开发和利用，如何减小和控制爆破振动对施工环境及周边建(构)筑物的危害已成为爆破振动安全研究领域亟需解决的问题，作为该领域的重要组成部分，爆破振动信号分析既是研究控制爆破振动危害的基础，也是科学制定抗震措施的前提。爆破振动信号作为各种频率成分振动波的混合体，经过复杂场地介质的滤波、放大作用后一般携带有能反映场地特性和爆破特征的重要信息，因此，为使爆破振动安全判据制定更加科学、完整，需要对信号中蕴含的时频、能量分布等重要特征信息进行准确提取[1-3]。然而，由于爆破振动测试易受外部环境和测试仪器的影响，获取的信号中往往掺杂有干扰噪声，只有通过信噪分离算法将有效的信号信息从中提取出来，才能保证爆破振动特征提取的可靠性和准确性。

爆破地震本身短时、突变、频率丰富的特点以及爆破区域场地、边界等条件的多变性加大了对爆破振动信号分析及特征提取的难度，并且传统的第一代小波变换由于不能根据信号特点选取适应的小波基来识别振动信号特征使其无法满足复杂信号在线处理的需要，然而，提升算法能够通过构造具有希望特性的小波函数从而得到与待分析信号相匹配的滤波器组，可以满足工程爆破大型网络化测试系统与控制平台对算法效率和精度等方面的要求。

提升算法(Lifting scheme)作为一种二代小波(Second Generation Wavelet，SGW)构造方法，继承了经典小波变换多分辨率的特性，变换仅在时域进行，可以实现原地运算，具有占用空间小、变换速度快、易于逆变换等优点[4-7]。目前在机械振动信号分析、故障诊断等方面的应用已比较成熟，段晨东[8]等通过提升算法准确提取了隐含在机械振动信号中的故障特征；周瑞[9]提出了一种基于二维第二代小波变换的机械振动信号压缩方法。近年来，谢全民[2]等学者尝试将提升算法引入到爆破振动信号的分析中，并取得了较为满意的效果。本文将在提升算法的基础上构造基于插值细分法的二代小波SGW(6,6)，并依据小波包变换思想，通过把改进最优基搜索算法引入到爆破振动信号的分析中，对提升算法在信噪分离以及能量特征分析等方面的应用效果进行了探讨，并取得了一些具有借鉴意义的结论。

1 提升小波包变换及相关算法

1.1 提升小波包变换

(1)

(2)

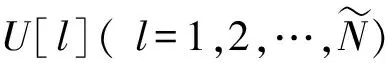
提升小波包变换的重构过程为分解过程的逆运算，可直接由分解过程得到，重构过程的预测器系数P和更新器系数U与分解过程相同。提升小波包变换的两层分解与重构过程如图1所示。

图1 提升小波包两层分解与重构过程

1.2 二代小波构造

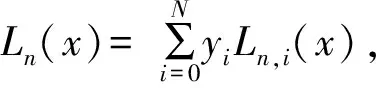
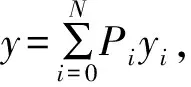
每一次细分时，取N(N=2D，D为正整数)个已知的样本yj,k-D+1,…,yj,k,yj,k+D，假设这些样本是等时间间隔采样的，它们对应的采样时刻分别为xk+1,xk+2,…,xk+N，xk为任意的起始时间，细分产生的新的采样值处于这些已知样本的中间位置。插值点为：x=xk+(N+1)/2，这样预测器系数可由式Ln,i(x)确定，即

(3)

根据式(3)即可求得SGW(6,6)的预测器系数如表1所示。更新器系数可直接由预测器系数除以2得出。预测器P和更新器U确定后，分别根据式(1)、式(2)经过迭代运算后便可得到小波函数ψ(x)与尺度函数φ(x)。

表1 SGW(6,6)的预测器系数

1.3 移频算法

基于等效滤波器概念[9]，提升小波变换的分解过程等效于信号经过高、低通滤波后再进行隔点采样，由于逐层隔点采样会导致每进行一层分解采样频率降低1/2，当其低于Nyquist频率时，高频成分继续分解会发生频率折叠，从而造成严重的频带错位，使分析结果失真。文献[13-14]中根据混频的原因提出了一种移频算法，将其引入提升小波包变换，则分解步骤中的式(1)和式(2)变为：

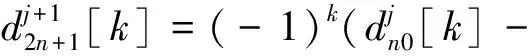
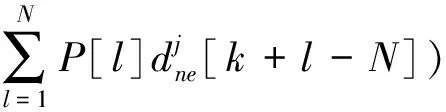
(4)

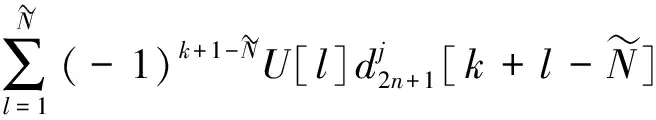
(5)

同理，重构步骤可由式(4)、式(5)逆运算求得。

2 最优基搜索算法

为说明改进搜索算法的优越性，本文将通过比较两种算法的空间复杂度以验证其空间效率。设信号长度为2M，提升小波包分解层数为CS，则原始搜索算法的空间复杂度为O[(CS+1)2M]；改进后的搜索算法所需的存储空间为：

2M+2×2M-1+2×2M-2+…+2×2M-CS=

2M×(1+1+2-1+…+2-(CS-1))=2M×(3-2-(CS-1))

(6)

因此，改进算法的空间复杂度为O[(3-2-(CS-1))2M]，则两种最优基搜索方法的存储空间之比为：

(7)

由式(7)可得Ra与CS之间的关系如图2所示。由图2可知，随着CS的增大，改进算法的空间效率较原始搜索算法明显提高，当CS=5时，Ra=0.49<0.5，说明改进后搜索算法的空间效率提高了1倍以上。

3 算法应用研究

图3(a)为结合某市政开挖工程采集的一实测爆破振动信号S的时程曲线图，试验仪器采用Exp4850型爆破振动测试仪，采样频率设为1 024 Hz，采样点数8 192，由振动波形可以看出，信号中掺杂有由测试系统自身带来的方波干扰。图3(b)为该信号的时频能量谱图，从该图也能发现(48～65) Hz的频段区间内存在高频噪声分量。

图2 Ra与CS之间关系图

3.1 在爆破振动信号降噪中的应用

3.1.1 降噪算法

基于提升小波包最优基分解算法的爆破振动信号的降噪步骤可分为：

(1) 在确定的分解层数CS下对信号进行提升小波包分解，同时根据最优基算法，选取代价函数最小的节点系数，最后得到信号S的最优小波包基；

(2) 对最优基下的各节点系数进行阈值量化。由于爆破振动信号具有很强的时频局部性，而软阈值处理后的信号相对平滑并会造成边缘模糊等失真现象，因此，本文采用硬阈值函数作为阈值量化函数。硬阈值函数的表达式为：

(8)

(9)

其中，噪声方差σ可由中位数估计法确定：

(10)

其中，median( )为中位数函数。

(4) 利用阈值量化后的小波包节点系数对信号逐层进行重构。

3.1.2 算例验证

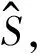
图4 最优提升小波包基各节点系数

3.1.3 信噪分离性能分析

为定量评价提升小波包最优基分解算法的信噪分离效果，文中引入信噪比(SNR)、均方根误差(RMSE)、峰值误差(PE)三项评价指标。

(11)

(12)

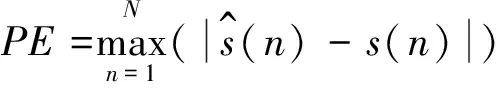
(13)

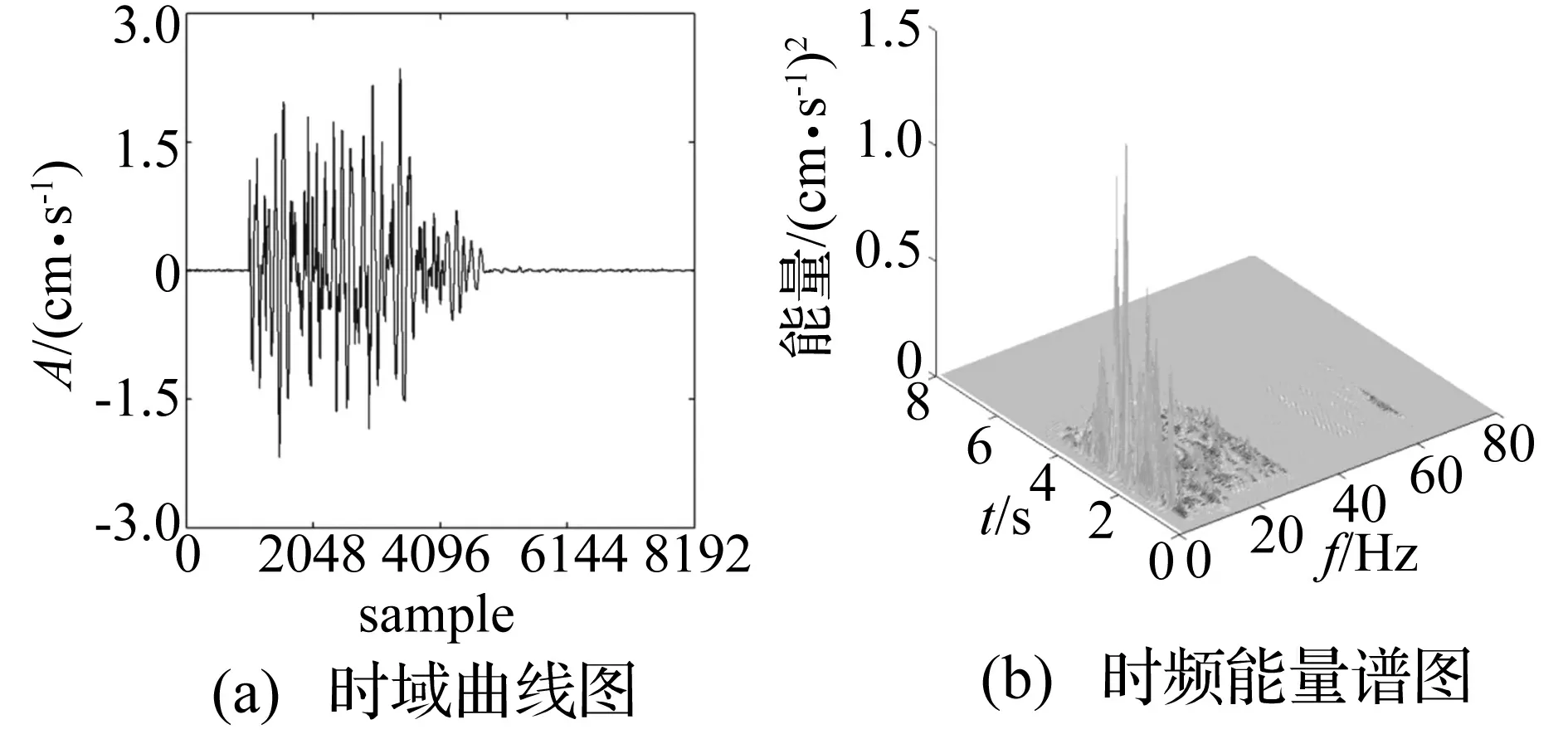
图5 信噪分离后信号的时程曲线及时频能量谱图

3.2 在爆破振动信号能量特征分析中的应用

在很多情况下，单一的质点振动速度指标不能完全反映建(构)筑物可能承受的破坏情况，而目标的破坏与结构响应是爆破震动引起的振动速度、频率、持续时间以及目标自身动力响应特性等因素综合作用的结果[15]，因此，本文将在提升小波包最优基分解算法的基础上，通过对能量特征分布的分析综合考察振动速度、频率及持续时间共同作用对建(构)筑物的影响。

3.2.1 爆破振动信号能量特征分析原理

爆破振动信号s(i)经提升小波包j层分解后，可得到2j个频带上的子空间信号，则s(i)可由这些子空间的正交和表示，即：

(14)

根据Parseval定理[16]，由式(18)可得爆破振动信号的能量为：

(15)

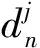
(16)

由式(14)、(15)可知，爆破振动信号可由提升小波包分解成不同频带的振动分量，从而反映了频率在爆破震动中的影响，且频带能量同时又是该频带振动分量的振动速度和作用时间的共同作用的结果，因此，能量特征分析在反映爆破振动信号振动速度、频率及作用时间对建(构)筑物影响方面具有一定的优势。

3.2.2 爆破振动信号不同频带的能量分布特征

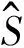
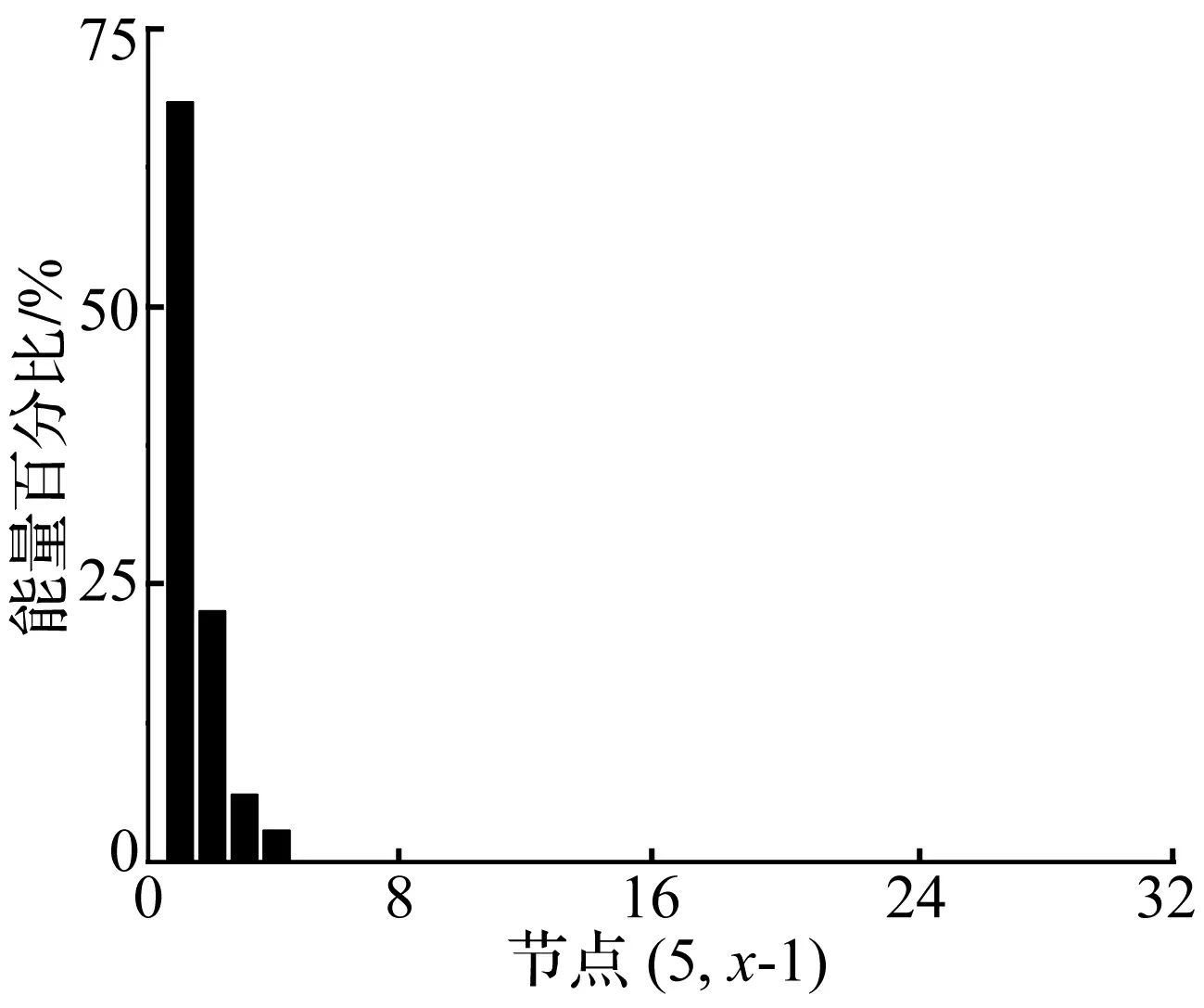
图7 爆破振动信号的能量分布规律

图8 功率谱密度

4 结 论

(1) 根据小波包变换具有多分辨率分析的特点，依据插值定理设计二代小波SGW(6,6)，并通过在分解过程中引进移频算法，有效解决了提升小波包变换时可能出现的相位失真及频率混叠现象；

(2) 改进的最优基搜索算法使得提升小波包的分解与最优基搜索过程同时进行，通过释放非最优基节点的小波包系数，很大程度上提高了算法的空间效率，当分解层数CS≥5时，其空间利用率提高1倍以上，因此，应用改进最优基搜索算法的提升小波包分解具有更好的在线信号处理性能；

(3) 提升小波包最优基分解算法能够快速有效滤除实测爆破振动信号中掺杂的噪声干扰，通过定量分析验证了该算法信噪分离效果理想，为后续的信号分析奠定了基础；

综上所述，基于最优基分解的提升小波包算法具有效率高、精度好、易于实现等优点，更加适合于复杂信号的在线处理，具有较好的应用前景，能够满足工程爆破大型网络化测试系统与控制平台对算法的要求。

参 考 文 献

[1]李洪涛, 舒大强. 爆破振动衰减规律的影响因素[J]. 武汉大学学报(工学版), 2005,38(1): 79-82.

LI Hong-tao, SHU Da-qiang. Influential factors analysis of blasting vibration attenuation law[J]. Engineering Journal of Wuhan University, 2005,38(1): 79-82.

[2]谢全民, 龙源, 钟明寿.SGWT在爆破振动信号信噪分离中的应用研究[J].振动与冲击, 2012,1 (31): 24-28.

XIE Quan-min, LONG Yuan, ZHONG Ming-shou. Application of SGWT in separation of noises from a blasting vibration signal[J]. Journal of Vibration and Shock, 2012,1 (31): 24-28.

[3]路 亮, 龙 源, 钟明寿. FastICA算法在低信噪比爆破振动信号信噪分离中的应用研究[J].振动与冲击, 2012,17(31): 33-37.

LU Liang, LONG Yuan, ZHONG Ming-shou. Separating nosie from a blasting vibration signal based on fast ICA[J]. Journal of Vibration and Shock, 2012,17(31): 33-37.

[4]张德丰. MATLAB小波分析[M]. 北京:机械工业出版社, 2009.

[5]姜洪开,何正嘉,段晨东. 基于提升方法的小波构造及早期故障特征提取[J]. 西安交通大学学报, 2005,39(5): 494-498.

JIANG Hong-kai, HE Zheng-jia, DUAN Chen-dong. Wavelet construction based on lifting scheme and incipient fault feature extraction[J]. Journal of Xi'an Jiaotong University, 2005,39(5): 494-498.

[6]Sweldens W. The lifting scheme: A construction of second generation wavelet[J]. SIAM Journal on Mathematics Analysis, 1997, 29(2): 511-546.

[7]Claypoole R L, Davis G M, Sweldens W, et al. Nonlinear wavelet transforms for image coding via lifting[J]. IEEE Transactions on Image Processing, 2003, 12(12): 1449-1458.

[8]段晨东,张建丁. 基于第二代小波变换的转子碰摩故障特征提取方法研究[J]. 机械科学与技术, 2006,25(10): 1229-1232.

DUAN Chen-dong, ZHANG Jian-ding. Study of the fault feature extraction method for rotor rub-impact based on the second generation wavelet transform[J]. Mechanical Science and Technology, 2006,25(10): 1229-1232.

[9]周 瑞. 基于第二代小波的机械故障信号处理方法研究[D]. 哈尔滨:哈尔滨工业大学, 2009.

[10]Sweldens W, Schröder P. Building your own wavelets athome[DB/OL].http://cm.bell-labs.com/who/wim/papes.html/at home, 1998-01-05.

[11]Sweldens W. The Lifting Scheme: A Custom-design construction of biorthogonal wavelets [J]. Applied and Computational Harmonic Analysis, 1996, 15(3):186-200.

[12]邓建中,刘之行. 计算方法(第二版)[M]. 西安:西安交通大学出版社, 2001.

[13]Coifman R, Wickerhauser M V. Entropy-based algorithms for best basis selection. IEEE Transaction on Information Theory,1992, 38(2): 713-718.

[14]曹建军. 基于提升小波包和改进蚁群算法的自行火炮在线诊断研究[D].石家庄:军械工程学院, 2007.

[15]中国生, 徐国元, 熊正明. 基于小波变换的爆破地震信号能量分析法的应用研究[J]. 爆炸与冲击, 2006,26(3): 222-227.

ZHONG Guo-sheng, XU Guo-yuan, XIONG Zheng-ming. Application research of the energy analysis method for blasting seismic signals based on wavelet transform[J]. Explosion and Shock Wave, 2006,26(3): 222-227.

[16]周德廉,邵国友. 现代测试技术与信号分析[M].徐州:中国矿业大学出版社, 2005.