饱和横观各向同性分数导数黏弹性土中半封闭衬砌振动响应

陈学丽, 闻敏杰， 高华喜

(1. 嘉兴职业技术学院 生物与环境分院，浙江 嘉兴 314036；2. 浙江海洋学院 船舶与建筑工程学院，浙江 舟山 316004)

以往对于饱和土中隧道动力响应研究主要存在以下两方面不足：一方面，将饱和土体视为各向均匀同性体。但土体在长期沉积和固结过程中存在各向异性，故横观各向同性地基模型较符合实际工程；另一方面，将土体等价为饱和多孔弹性介质或利用经典黏弹性模型来描述土骨架的黏性。孙海忠和张卫[1]已证明该模型在描述黏弹性行为时不能与实验数据很好吻合，而分数导数本构模型更精确地反映土体蠕变的全过程。分数导数模型自Gernent[2]提出来后，Bagley等[3-4]进行了完善，之后不少学者将其用于研究黏弹性材料[5-7]，最近在地基、桩基等工程中得到应用[8,9]。然而，在描述横观各向同性土体的动力学行为方面，笔者未见报道。

近年来，Lu等[10-12]将土体视为饱和均匀弹性介质，分别研究了简谐荷载、冲击荷载和单级荷载作用下圆形隧道的稳态或瞬态响应；将土体视为均匀黏弹性介质，Xie等[13-15]根据Voigt[16]提出并被其它学者[17-19]所用的经典黏弹性模型描述土骨架的黏性，研究了饱和黏弹性土—隧道壳体衬砌耦合振动特性；将土体视为饱和横观各向弹性体，刘干斌等[20]对圆形隧道开挖引起的应力和位移进行了分析，而忽略了土体惯性和衬砌厚度的影响。将土体视为单相横观各向黏弹性体，阿查亚等[21]讨论了高阶黏弹性、黏弹性参数的非均质性对径向位移和应力的影响。

在现有研究基础上，本文首先假设横观各向同性面和垂直于该面的土体黏性相同，将土骨架视为具有分数导数本构关系的横观各向同性粘弹性体，采用饱和多孔介质理论，得到了简谐荷载作用下饱和横观各向同性黏弹性土的位移、应力和孔隙水压力解析表达式；再次，将衬砌视为均匀弹性体，求得了弹性衬砌的应力和位移表达式；然后，利用衬砌内边界应力协调以及土体和衬砌界面处应力和位移连续，得到了相关待定系数的具体表达式。最后，考察了饱和经典弹性土、饱和分数导数性黏弹性土和饱和经典黏弹性土三种条件下饱和黏弹性土和衬砌各物性和几何参数对系统动力响应的影响。

1 数学模型

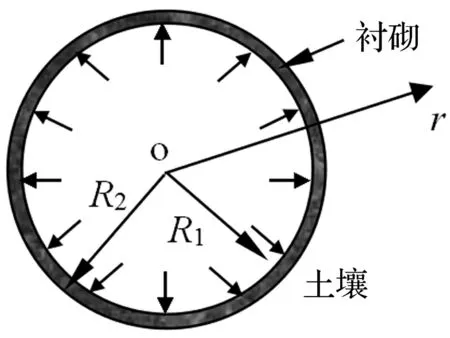
图1 横观各向同性土—隧洞衬砌动力相互作用

如图1所示，无限饱和横观各向同性黏弹性土中一深埋圆形衬砌隧道。衬砌内外半径分别为R1和R2，其厚度为d=R2-R1；横观各向同性面内的弹性模量和泊松比分别表示为E1和μ1；垂直于横观各向同性面内的弹性模量和泊松比分别为E2和μ2；若土颗粒和孔隙流体的体积分数分别为nS和nF，记土颗粒和孔隙流体的真实密度为ρSR和ρFR，则表观密度为ρS=nSρSR和ρF=nFρFR；衬砌密度和泊松比分别为ρL和vL，而其弹性模量为EL。现衬砌内边界作用径向均布简谐荷载q0eiωt(i2=-1)，ω为角频率。另外，假设衬砌中水头为P1=0；土体中水头为P2=p。设衬砌和土体完全接触且衬砌不产生变形，又忽略衬砌中孔隙水的影响。根据Li[22]结合实际工程模型，建立的隧道部分透水边界条件，可令衬砌和土体界面处无积水，即衬砌中流体速度与土体中流体速度在界面处相等。

2 土体控制方程

忽略土骨架和孔隙流体的压缩性，根据饱和多孔介质理论[23-24]，得到土体的固相动量方程、孔隙流体动量方程及体积分数守恒引起的质量平衡方程分别为[25,26]

(1)

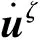
σS=-nSpI+σSE

σF=-nFpI

pF=-pS=pgradnF+pFE

}

(2)

式中，p和σSE为孔隙水压力和有效应力张量；pFE表示有效孔压。根据体积分数概念和不可压缩条件，体积分数满足如下平衡方程

nS+nF=1

(3)

因此，总应力张量可表示为

σT=σF+σS=-pI+σSE

(4)

有效孔隙水压力pEF满足下列式

(5)

式中，Sv=(nF)2γFR/kF为表征流固两相的相互作用系数，而γFR=ρFRg为流相重度，kF为Darcy渗流系数。

假设横观各向同性面内土骨架的黏性和垂直于横观各向同性面内土骨架黏性相同，利用分数导数黏弹性模型描述土骨架的应力—位移本构关系[9]:

(6)

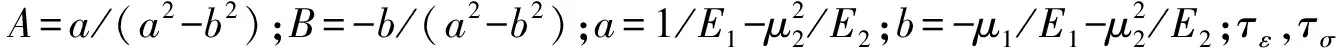
(7)

对于稳态振动，记

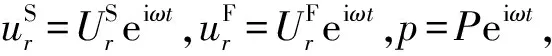
(8)

(9)

(10)

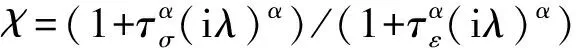
利用式(8)-(10)，可易解得径向位移为:

(11)

式中，

(12)

其中，C1,C2为待定系数，K1(·)为1阶第二变形Bessel函数。

又利用式(10)和式(11)，解得:

(13)

于是，由式(9)、式(11)和式(13)，解得孔隙水压力为:

(14)

由式(14)可见，lnr是发散函数。为满足r→∞,p→0，引入大数K，使p=0(K=0)

(15)

由此可得，

(16)

杨骁和闻敏杰[27]已证明当大数K=60时该发散函数对响应幅值无任何影响。

式中，

(17)

利用本构关系式(6)，可得土骨架有效应力为:

(18)

再由式(18)和有效应力原理式(4)，可得土体总应力为:

(19)

3 衬砌控制方程

(20)

式中，

(21)

由式(20)易解得

(22)

式中，C5,C6为待定系数。

于是，衬砌径向应力为:

(23)

式中，

(24)

4 连续性边界条件

假设衬砌和土体完全紧密接触，无相对滑移，则在界面处(r=R2)满足

(25)

衬砌内边界(r=R1)作用均布轴对称简谐荷载，则满足:

(26)

根据Li[22]采用Darcy渗透定律，解决的实际隧道工程中边界渗透性问题，则衬砌中的流体流量为:

(27)

式中，kL为衬砌的Darcy渗透系数。

而土体中流体流量为:

(28)

显然，上述两者流体流量在衬砌和土体界面处(r=R2)相等，则:

(29)

式中，κ=kL/kFR2(lnR2-lnR1)为衬砌和土体相对渗透系数，由衬砌的几何尺寸决定。当kL≪kF时，κ→0，边界不渗透，衬砌处于封闭状态；当kL≫kF时，κ→∞，边界为自由渗透，衬砌为不封闭状态。

至此，利用边界条件式(25)-(29)，即得到待定系数C1,C2,C5,C6的具体表达式，从而得到饱和横观各向同性分数导数黏弹性土中深埋圆形半封闭衬砌隧道稳态动力响应解析解。

5 计算结果分析

考察土体和衬砌各参数对径向位移幅值的影响。图2～图4分别表示横观各向同性饱和弹性土(α=0)、横观各向同性饱和分数导数型黏弹性土(α=0.5)和横观各向同性饱和经典黏弹性土(α=1)条件下弹性模量E1对衬砌和土体界面处(r=3.25)径向位移幅值的影响。图2～图4综合可见，系统产生明显的共振效应且随着弹性模量E1的增加，共振效应逐渐减弱，径向位移幅值的峰值减小，而基频却逐渐增大。这是由于横观各向同性面的弹性模量E1增大，土体的阻抗越大所引起的。另外，从该三图我们发现，横观各向同性饱和分数导数型黏弹性土(α=0.5)时位移幅值的峰值小于横观各向同性饱和弹性土(α=0)时位移幅值的峰值，却大于横观各向同性饱和经典黏弹性土(α=1)时位移幅值的峰值。而横观各向同性饱和分数导数型黏弹性土(α=0.5)时系统产生共振的基频大于横观各向同性饱和弹性土(α=0)时的基频，却小于横观各向同性饱和经典黏弹性土(α=1)时的基频。这充分说明将土体视为弹性土(α=0)时高估了弹性模量E1对位移幅值的影响，将土体视为经典黏弹性土(α=1)时却低估了弹性模量E1对位移幅值的影响。而且，可以通过改变阶数取值来改变弹性模型E1对位移幅值的影响。图5～图7分别表示在r=4处横观各向同性饱和弹性土(α=0)、横观各向同性饱和分数导数型黏弹性土(α=0.5)和横观各向同性饱和经典黏弹性土(α=1)条件下衬砌厚度d对径向位移幅值的影响。图5～图7可见，衬砌厚度对位移幅值的影响与土骨架的黏性有明显关系。随着分数导数阶数的增加，衬砌厚度变化对位移幅值的峰值影响逐渐减小，这是由于阶数增加时，土体的阻抗逐渐增大所造成的。另外，随着衬砌厚度的增加，共振效应减小，而相应的基频逐渐增大，是因为衬砌厚度增加时，衬砌的刚度增大所引起的。图8表示在r=4处衬砌和土体的相对渗透系数对径向位移幅值的影响。可见，渗透系数更好地反映了隧道边界的渗透特性。渗透系数越小，界面处越接近不透水状态，则在稳态振动时，共振效应越明显。而当渗透系数分别为κ=100和κ=1 000时，位移幅值几乎无任何变化，此时说明边界已经达到自由渗透状态。图9～图11分别表示横观各向同性饱和弹性土(α=0)、横观各向同性饱和分数导数型黏弹性土(α=0.5)和横观各向同性饱和经典黏弹性土(α=1)条件下弹性模量E1对衬砌和土体界面处(r=3.25)的孔隙水压力幅值影响。由图9～图11比较看出，横观各向同性面的弹性模量E1对孔隙水压力幅值的影响与土骨架黏性也有密切关系，当横观各向同性饱和弹性土(α=0)时，随着弹性模量E1的增加，孔压幅值的峰值呈增大趋势，横观各向同性饱和分数导数黏弹性土(α=0.5)时，当弹性模量E1增加时，孔压幅值峰值明显减小，而横观各向同性饱和经典黏弹性土(α=1)时，当弹性模量E1增加时，孔压幅值峰值呈减小趋势，但影响不大。这也充分说明弹性模量E1对孔压幅值的影响与分数导数阶数有明显关系。图12～图14分别为在r=4处横观各向同性饱和弹性土(α=0)、横观各向同性饱和分数导数型黏弹性土(α=0.5)和横观各向同性饱和经典黏弹性土(α=1)条件下衬砌厚度d对孔压幅值的影响。图12～图14比较分析得衬砌厚度在横观各向同性饱和弹性土(α=0)时对孔压幅值的峰值影响明显，而在横观各向同性饱和分数导数型黏弹性土(α=0.5)和横观各向同性饱和经典黏弹性土(α=1)条件下对孔压幅值峰值影响较小。图15为相对渗透系数对孔压幅值的影响。可见，渗透系数对孔压幅值的影响与对位移幅值的影响有类似之处，随着渗透系数的增加，共振效应越不明显。

图2 横观各向同性饱和弹性土(α=0)时弹性模量E1对径向位移幅值影响

图6 横观各向同性饱和分数导数黏弹性土(α=0.5)时衬砌厚度d对径向位移幅值影响

图10 横观各向同性饱和分数导数黏弹性土(α=0.5)时弹性模量E1对孔压幅值影响

图14 横观各向同性饱和经典黏弹弹性土(α=1)时衬砌厚度d对孔压幅值影响

图15 相对渗透系数κ对孔压幅值影响

6 讨 论

土体是典型的黏弹性材料，其黏性在高温或加载时间影响下表现极为突出。与以往的经典Maxwall、Kelvin和广义Maxwall等黏弹性模型[29-30]相比，分数导数本构关系可更好地反映土体在整个加载和卸载过程中的变形特性。但由于利用分数导数本构关系建立的动力方程为具有奇异性的积分—偏微分方程，它们的定性分析和数值计算较困难[31]。目前，国内外还处于起步阶段，特别是在参数取值方面，虽然何利军等[32]通过固结试验给出了不同围压下分数导数模型相关参数取值，但只推导了软黏土的蠕变模型，未考虑土体的动力学行为，故在模型参数确定上仍需做大量工作。

7 结 论

本文将土骨架视为横观各向同性黏弹性体，利用分数导数模型描述饱和横观各向同性黏弹性土的力学行为，研究了饱和横观各向同性分数导数黏弹性土体中深埋圆形隧道半封闭衬砌稳态振动响应，得到如下结论：

(1) 稳态振动时，横观各向同性面的弹性模量E1对系统动力响应的影响与土体的黏性有密切关系。当横观各向同性饱和经典黏弹性土(α=1)时，弹性模量E1对系统共振的基频最大，而对横观各向同性饱和弹性土(α=0)、横观各向同性饱和分数导数型黏弹性土(α=0.5)时基频影响相对较小。

(2) 衬砌厚度对系统动力响应影响也与土体的黏性有关。在横观各向同性饱和弹性土(α=0)时，随着衬砌厚度增加系统动力响应明显减小，而横观各向同性饱和经典黏弹性土(α=1)和横观各向同性饱和分数导数型黏弹性土(α=0.5)时衬砌对系统动力响应影响较小。

(3) 渗透系数更好地描述界面的渗透特性，边界不透水时系统产生明显的共振现象，而随着渗透系数的增加，共振效应减弱。

参 考 文 献

[1]孙海忠，张 卫. 服从分数导数Kelvin本构模型的粘弹性阻尼器的阻尼性能分析及试验研究[J]. 振动工程学报， 2008，21(1)：48-53.

SUN Hai-zhong, ZHANG Wei. Analysis and experiment on damping properties of visco-elastic damper modeled by fractional Kelvin method[J]. Journal of Vibration Engineering，2008，21(1)：48-53.

[2]Gement A. On fractional differences[J]. Phil Mag，1938，25(1)：92-96.

[3]Bagley R L, Torvik P J. A theoretical basis for the application of fractional calculus to viscoelasticity[J]. Journal of Rheology, 1983, 27(3): 201-210.

[4]Koeller R C. Applications of the fractional calculus to the theory of viscoelasticity[J]. Journal of Applied Mechanics, 1984, 51(3): 294-298.

[5]Padovan J. Computational algorithms for FE formulations involving fractional operators[J]. Computatinal Mechanics, 1987, 4(2): 271-287.

[6]Shimizu N，Zhang W. Fractional calculus approach to dynamic problem of viscoelastic materials[J]. JSME International JournalSeries C, 1999, 42(1): 827-830.

[7]刘林超, 闫启方, 孙海忠. 软土流变特性的模型研究[J]. 岩土力学, 2006, 27(增刊2): 214-217.

LIU Lin-chao, YAN Qi-fang, SUN Hai-zhong. Study on model of rheological property of soft clay[J]. Rock and Soil Mechanics, 2006, 27(Supp.2): 214-217.

[8]刘林超，杨 骁. 竖向集中力作用下分数导数型半无限体粘弹性地基变形分析[J]. 2009, 26(1): 13-17.

LIU Lin-chao，YANG Xiao. Analysis on settlement of semi-infinite viscoelastic group based on fractional derivative model[J]. Engineering Mechanics，2009，26(1)：13-17.

[9]刘林超，杨 骁.分数导数模型描述的饱和土桩纵向振动分析[J]. 岩土力学，2011，32(2)：526-532.

LIU Lin-chao, YANG Xiao. Analysis of vertical vibrations of a pile in saturated soil described by fractional derivative model[J]. Rock and Soil Mechanics, 2011, 32(2): 526-532.

[10]Lu J F, Jeng D S. Dynamic analysis of an infinite cylindrical hole in a saturated poroelastic medium[J]Archive of Applied Mechanics, 2006, 76(5-6): 263-276.

[11]高 盟, 高广运, 王 滢, 等. 均布突加荷载作用下圆柱形衬砌振动响应的解析解[J]. 岩土工程学报, 2010, 32(2): 237-242.

GAO Meng, GAO Guang-yun，WANG Ying, et al. Analytical solution on dynamic response of lining subjected to sudden internal uniform loading[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(2): 237-242.

[12]刘干斌，谢康和，施祖元，等. 压力隧洞衬砌-围岩(土)相互作用研究[J]. 岩石力学与工程学报, 2005, 24(14): 2449-2455.

LIU Gan-bin，XIE Kang-he，SHI Zu-yuan，et al. Interaction of surrounding rock or soil and lining of a pressure tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(14): 2449-2455.

[13]Xie K H，Liu G B，Shi Z Y. Dynamic response of partially sealed circular tunnel in viscoelastic saturated soil[J]. Soil Dynamics Earthquake Engineering, 2004, 24(12): 1003-1011.

[14]Liu G B，Xie K H. Transient response of a spherical cavity with a partially sealed shell embedded in viscoelastic saturated soil[J]. Journal of Zhejiang University Science, 2005, 6A(3): 194-201.

[15]蔡袁强，陈成振，孙宏磊. 黏弹性饱和土中隧道在爆炸荷载作用下的动力响应[J]. 浙江大学学报，2011，45(9)：1657-1633.

CAI Yuan-qiang, CHEN Chen-zhen, SUN Hong-lei. Dynamic response of tunnel in viscoelastic saturated soil subjected to blast loads[J]. Journal of Zhejiang University(Engineering Science), 2011, 45(9)：1657-1633.

[16]Voigt W. Theortische student uber die elasticitatsverhlinisse krystalle[J]. Abh Ges Wiss Goettingen, 1887, 34(1): 21-34.

[17]Das T K, Sengupta P R. Effect of damping on the torsional vibration of a homogeneous viscoelastic circular cylinder including strain rate stress rate[J]. Acta Ciencia Indica, 1991, 17(2): 271-280.

[18]Biswas P K，Sengupta P R. Torsional vibration of a non-homogenous viscoelastic circular cylinder involving strain and stress rate of higher order[J]. Acta Ciencia Indica，1991, 17M(2): 747-754.

[19]Sengupta P R, De N, Kar M, et al. Rotatory vibration of sphere of higher order viscoelastic solid[J]. Internal J Math Sci, 1994, 17(4): 799-806.

[20]刘干斌, 谢康和, 施祖元, 等. 横观各向同性土中深埋圆形隧道的应力和位移分析[J]. 岩土工程学报, 2003, 25(6): 727-731.

LIU Gan-bin, XIE Kang-he, SHI Zu-yuan. Analysis of stress and displacement around a deep circular tunnel in transversely isotropic soil[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(6): 727-731.

[21]阿查亚 D P，因德拉吉罗伊，比沃斯 P K. 无限非均质横观各向同性黏弹性介质中具有圆柱孔洞时的振动[J]. 应用数学和力学, 2008, 29(3): 331-341.(海治译)

[22]LI X. Stress and displacement fields around a deep circular tunnel with partial sealing[J]. Computers and Geotechnics, 1999, 24(2): 125-140.

[23]Bowen R M. Incompressible porous media models by use of the theory of mixtures[J]. International Journal of Engineering Science, 1980, 18(9): 1129-1148.

[24]Bowen R M. Compressible porous media models by use of the theory of mixtures[J]. International Journal of Engineering Science, 1982, 20(6): 697-735.

[25]Deboer R，Ehlers W，Liu Z F. One-dimensional transient wave propagation in fluid-saturated incompressible porous media[J]. Archive of Applied Mechanics, 1993, 63(1): 59-72.

[26]Yang X. Gurtin-type variational principles for dynamics of a non-local thermal equilibrium saturated porous medium[J]. Acta Mechanica Solida Sinica, 2005, 18(1): 37-45.

[27]杨 骁, 闻敏杰. 饱和分数导数粘弹性土-隧洞衬砌系统的动力特性[J]. 工程力学, 2012, 29(12): 248-255.

YANG Xiao，WEN Min-jie. Dynamic characteristics of saturated fractional derivative type viscoelastic soil and lining system with a deeply embedded circular tunnel[J]. Engineering Mechanics, 2012, 29(12): 248-255.

[28]Yang X, Pan Y. Axisymmetrical analytical solution for vertical vibration of end-bearing pile in saturated viscoelastic soil layer[J]. Applied Mathematics and Mechanics, 2010, 31(2): 193-204.

[29]陈晓平，白世伟. 软土蠕变-固结特性及计算模型研究[J]. 岩石力学与工程学报，2003，22(5)：728-734.

CHEN Xiao-ping, BAI Shi-wei. Research on creep-consolidation characteristics and calculating model of soft soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(5): 728-734.

[30]Yin J H，Graham J. Elastic visco-plastic modeling of one-dimensional consolidation[J]. Geotechnique, 1996, 46(3): 515-527.

[31]朱正佑, 李根国, 程昌钧. 具有分数导数本构关系的黏弹性Timoshenko 梁的静动力学行为分析[J]. 应用数学和力学, 2002, 23(1): 1-10.

ZHU Zheng-you, LI Gen-guo, CHENG Chang-jun. Quasi-static and dynamical analysis for viscoelastic Timoshenko beam with fractional derivative constitutive relastion[J]. Applied Mathematics and Mechanics, 2002, 23(1): 1-10.

[32]何利军，孔令伟，吴文军，等. 采用分数阶导数描述软黏土蠕变的模型[J]. 岩土力学，2011，32(增刊2)：239-244.

HE Li-jun，KONG Ling-wei，WU Wen-jun，et al. A description of creep model for soft soil with fractional derivative[J]. Rock and Soil Mechanics, 2011, 32(Supp. 2): 239-244.