声发射信号在不同结构轴中传播特性研究

肖俨衍, 卢文秀, 褚福磊

(清华大学 机械工程系, 北京 100084)

声发射信号是材料变形或破坏时应变能释放而产生的瞬态弹性波[1]。因为声发射信号本身有着动态性、敏感性、整体性和及时性[2]等优点，近年来在石油化工、电力、交通运输、航空航天中都得到了广泛的应用。

目前的声发射研究绝大多数集中在缺陷源定位[3-4]以及提取故障信息[5-6]这两方面，较少涉及声发射信号的传播特性。而声发射信号在传播介质中的传播特性会对准确获取故障信息产生影响[7-8]，故研究其传播特性具有重要意义。

Breckenridg在1975年证明声发射信号是一种弹性波，研究声发射信号的传播特性本质上是研究弹性波的传播特性。Yih-Hsing[9]较早地系统性地研究了声发射信号传播的基本特性。龚仁荣[10]建立了声发射信号的一维和二维传播模型，并利用模型进行了简单的定位分析，并运用Gabor小波分析方法对信号进行分析提出了新的源定位方法研究。

由上可知，目前声发射信号传播特性研究主要研究内容为平面、一维圆杆等抽象对象，而较少针对具体机械部件进行研究。旋转机械中裂纹、碰摩等故障都会产生声发射信号。然而在进行源定位或故障识别时，传感器获得的含有故障信息的声发射信号都必须经过不同结构轴的传播，故研究声发射信号在不同结构轴中的传播特性对提取更准确的声发射源信息有重要意义。郭福平[11]重点对声发射信号在波导杆中的传播特性进行了实验研究，其实验的内容包括7种不同直径，3种不同长度的波导杆信号传播影响研究。

本文利用二维有限差分方法建立了声发射信号在三种最常见轴中的传播模型(光轴、阶梯轴、阶梯退刀槽轴)，研究了不同结构轴对声发射信号传播的影响。利用PAC声发射采集系统进行了一系列实验，对声发射信号在仿真情况中的传播进行了实验研究。

1 模型建立

二维有限差分是建立声发射信号在轴中传播模型最有效的方法之一。Glimm等[12]较早地进行了一维双曲型偏微分方程有限差分方法的研究。Hirose[13]提出了时域边界单元法，且将其运用于轴对称物体弹性波传播特性研究，但其方法运用于双曲型微分方程的有限差分格式时却没有那么顺利。Xiao等[14]利用规则网格差分格式对圆杆、圆头杆等在冲击应力波输入下进行了数值仿真研究，获得了很有价值的结果。

如图1所示的光轴、阶梯轴中，假设轴的材料均为各向同性、线弹性体且无扭转变形，声发射信号传播的动力学方程如下。

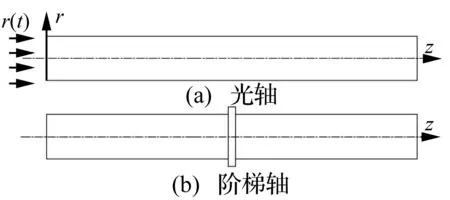
图1 光轴、阶梯轴

图2 矩形单元坐标定义

(1)

式中:r,z,θ为圆柱体坐标,t为时间,τrr,τzz,τθθ,τrz为应力分量，vr,vz为r，z方向上的质点速度，c1,c2为纵波和横波传播的速度,μ=1-2(c2/c1)2为各向同性材料系数。为了方便计算，可以将式(1)转换为矩阵形式:

(2)

考虑到矩阵φ,φ1,φ2,φ3可以通过转换矩阵联系起来有:

(3)

其中:φ1=Z1·φ,φ2=Z2·φ,φ3=Z3·φ

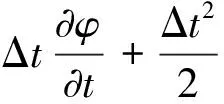
(4)

将式(2)，式(3)代入式(4)中消去φ的一阶偏导数(二阶项略去)，加入声发射信号传播过程中的衰减系数，即可以得到弹性波有限差分格式，建立仿真模型。利用此方法得到的是一个二阶精度的差分格式，其可以用来计算轴对称不同外形(正规，圆形，椭圆等)边界固体在冲击和连续应力下的二维响应。

2 仿真计算

2.1 光轴仿真

在如图1(a)所示的光轴中，长度z=40 mm, 半径r=8 mm,ρ=7.85 g/cm3,c1=5 mm/μs,c2=3.25 mm/μs。t=0时其左端面处承受一个模拟声发射脉冲(如图3(a)所示)，且为均布载荷。将轴沿r方向分为8个单元，z方向分为40个单元，考察光轴右端面中心节点的响应。

从图3(b)可以得出逐次反射波峰之间时间间隔为ΔT=15.8 μs，这个时间间隔与信号在轴中传播一个来回所需要的时间ΔT=2*z/c1=80/5=16 μs近似相等。由此可知，影响声发射信号在光轴中传播的主要是反射效应，且信号经过逐次反射之后将呈指数规律衰减。此外，注意到经过4次反射之后的波形将明显发生畸变。

由图3(b)和图3(c)的 对比得出，当长径比为5/1时，波形产生畸变较明显。而当长径比增大到20/1时，形畸变将越来越小，即趋近于一维传播情况。

2.2 阶梯轴仿真

在如图1(b)与图4(a)所示的阶梯轴中，材料参数与光轴相同，半径r1=8 mm,径向分为8个网格， 长度方向z1=z3=120。其中，阶梯处r2=13 mm径向为13个网格，长度方向为z2=16个网格。当波传到阶梯处分别对界面1和界面2会有两种不同边界条件处理：对于界面2，其两边节点于应力与速度等参数连续；对于边界1上节点做自由表面处理；对于边界1与边界2的交点，其参数无法直接由常规方法计算，可由其相邻节点参数利用最小二乘法近似给出。

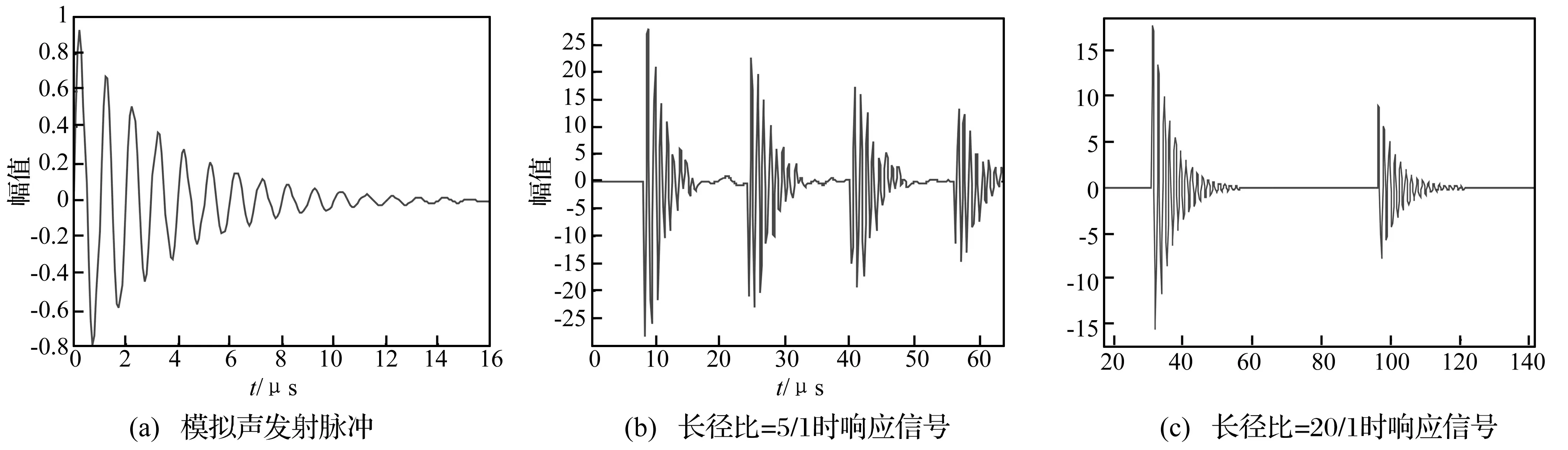
图3 光轴仿真结果

图4(b)是使用与光轴相同的输入信号得到的轴右端中线节点响应曲线。从图中可以得出响应信号三次波峰之间时间间隔ΔT1≈ΔT2=51.4μs，这个时间间隔与声发射信号在阶梯轴轴端与阶梯处中传播一个来回所需要的时间即ΔT=2L/c1=256/5=51.2μs近似相等。由此可知，由于阶梯的存在，信号通过阶梯处时会发生明显的反射，且由于阶梯处有两个发射界面，其两次反射波形会发生叠加，使得波形会发生改变。从2，3个波峰之间幅值对比得出，阶梯处发生反射的信号幅值与轴端反射相比较小。3次反射波的时域宽度依次为20.12 μs， 25 μs，30.26 μs，可见多次反射同样会使得波的能量越来越分散。

图4(c)改变了阶梯高度，第二次反射波峰幅值增大，即由于阶梯高度增加，阶梯界面的反射相应地增加了。而第一个反射波峰减小，即根据能量守恒，阶梯处透射波幅值减小。由于反射界面位置没有改变，故3次反射波形位置没有改变。

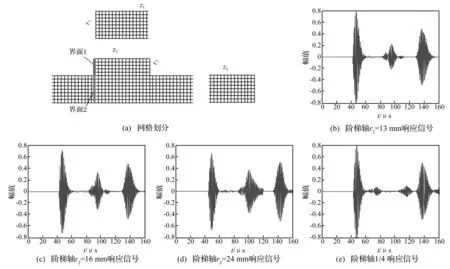
图4 阶梯轴仿真结果

图4(d) 第1,2号反射波峰时间间隔有所增大，阶梯处反射波峰变宽，幅值增大，即阶梯宽度的增加使得在阶梯界面处反射增强；两次反射时间间隔改变，反射波峰波形变宽，波峰位置发生相应改变。同样，第一次波峰幅值有所减小，即阶梯处透射能量减小。

改变阶梯位置到1/3处即z1=60，z3=180。从图4(e)可以看出，第2,3号反射波峰分别为入射信号通过阶梯处反射波峰和轴端反射之后经过阶梯处的反射波峰。且1,2与3,4波峰之间时间间隔ΔT=34 μs等于信号从阶梯处与轴端传播一个来回所需时间。

由上可知，当阶梯高度发生改变时，阶梯处的反射、透射信号的幅值会发生改变；当阶梯宽度改变时，阶梯处透射信号的幅值，反射信号的位置、宽度、幅值都会发生改变；而当改变阶梯位置时，阶梯处反射信号的位置、幅值会发生改变。改变其中任一个参数，信号的波形都会发生一定改变。

2.3 阶梯轴-退刀槽仿真

在实际情况中，阶梯轴上还经常会有退刀槽等结构，其对声发射信号传播特性的影响也不可忽视。如图1(c)与4(a)所示的尺寸相同的阶梯轴中存在一个退刀槽(如图所示)，其深度为0.5 mm，宽度为1 mm，位置在阶梯与轴端正中处。因为退刀槽深度较小且此处传播情况较为复杂，故在仿真中对槽所在位置处的网格进行加密处理，网格密度是普通网格密度的4倍(网格处理如图5(a)所示)。

图5(b)是使用与阶梯轴相同的输入信号得到的轴中线节点的响应信号。从波形时域图来看，以到达时刻先后可以得出几次反射波峰的主要来源：1号波峰为信号最先到达波峰；2号波峰s是由轴端反射之后的信号经退刀槽处反射波形；3号波峰是由阶梯处产生的反射波形；4号波峰则是由入射信号直接经退刀槽处反射后又经轴端反射产生的波形；5号波峰为从两次轴端反射波峰(之后重复)。退刀槽的存在对信号的传播会有两方面的影响，其一是由于槽本身对于传播过的信号产生影响；其二是其本身也会产生反、透射信号，从而影响信号在阶梯退刀槽轴中传播的整体情况。从幅值来看，轴端处反射的波形幅值最大，其次为阶梯处反射波形，从退刀槽处反射波形幅值最小。值得注意的是退刀槽处前后两次反射波形由于反射之后传播路径长短不一，故传播路径长的衰减幅度大，所以4号波峰峰值最小。而从波形上来看，经过退刀槽处反射的波峰变化最大。而与阶梯轴相同的是，反射次数的增加同样使得波的能量越来越分散。

图5(c)改变了退刀槽的深度，波峰到达时间以及幅值大小关系并无明显改变，但是从波形中可以看出，退刀槽处反射信号幅值有所增强，透射信号幅值有所减小；且因为退刀槽深度的增加，波形畸变更加严重。

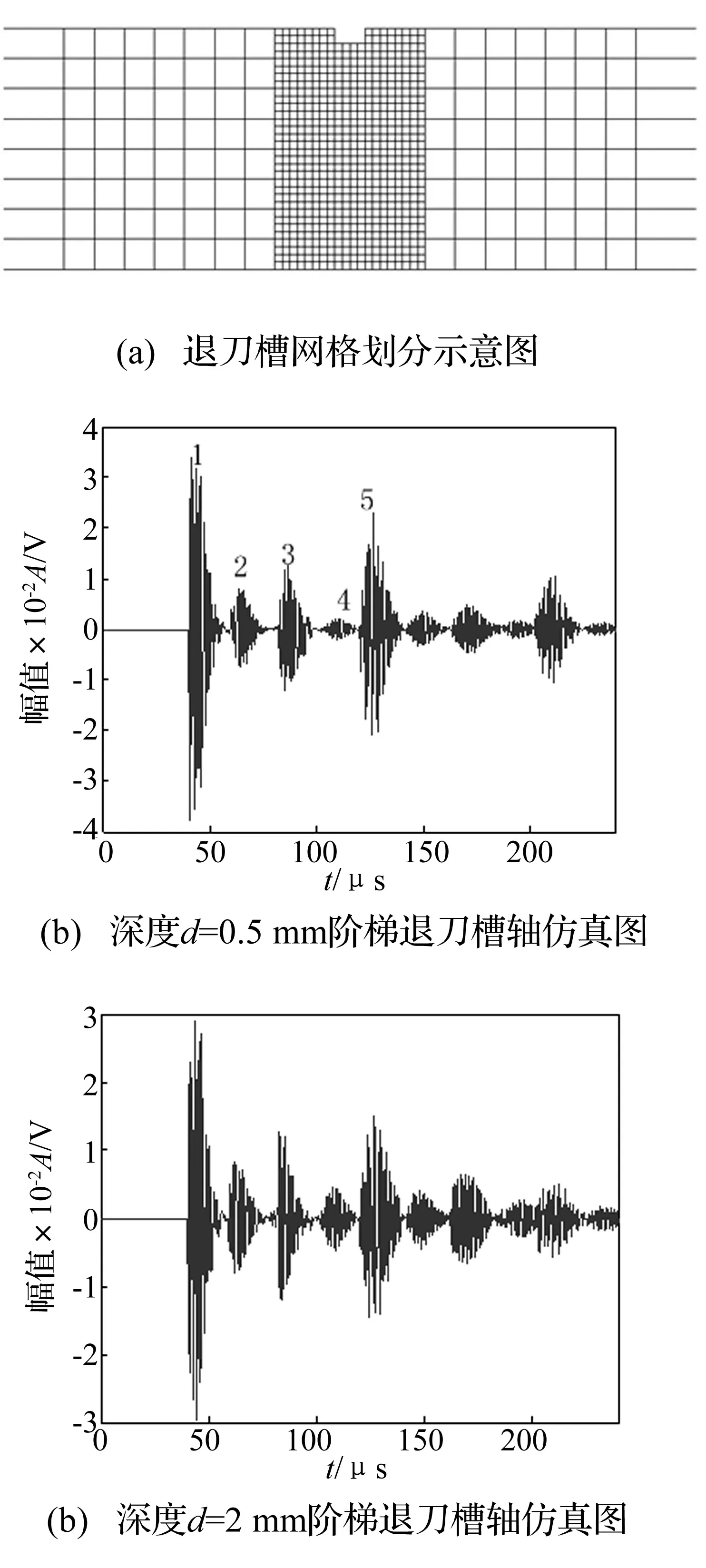
图5 阶梯缺陷轴仿真图

3 实验-仿真分析

实验台如图6(a)所示，实验轴处于自由应力状态，且传感器两端都用精确扭力扳手拧紧以确保每次都使用的同样拧紧力。利用信号发生器作为激励源，激励信号频率为150 kHz或300 kHz，幅值为1V的单正弦脉冲，由于传感器的频率特性，实际入射激励信号如图6(b)所示。实验使用的传感器是美国PAC 公司的R15，R30以及WD型传感器，信号经过40 dB前置放大，采样频率为5 MHz。

图6 实验准备图

3.1 光轴实验-仿真

实验采用的轴直径为16 mm，长度为400 mm，材料为钢，入射信号频率为150 kHz。

将图7(a)与图7(b)对比可得，光轴实验仿真信号具有明显的反射特征，同时其不同反射波峰间的幅值衰减为10.70 dB，8.21 dB，5.10 dB，且随着反射次数的增加，波形宽度越来越宽。仿真信号则能够较好地模拟反射波峰分布以及幅值的衰减，且波形有一定相似度。注意到实验波形会有趋向“扇形”的趋势，这有可能是由于信号在传感器与轴接触界面间的二次反射造成的，使用非接触传感器(如光纤声发射传感器)将得到与仿真波形更加接近的信号。

3.2 阶梯轴实验-仿真

实验采用的轴直径为16 mm，长度为400 mm，材料为钢。阶梯处位于轴中心，直径为25 mm，宽度为4 mm，入射信号频率为150 kHz。

将图7(c)与图7(d)对比得，声发射信号在阶梯轴中的传播比光轴复杂，不同波型(横波、纵波等)叠加，频散等效应使得畸变更加严重。但前5号反射波峰仍能从实验响应信号中读出，且仿真结果与实验结果逐次反射波峰时间间隔、幅值相符合。2号反射波峰幅值小于3号反射波峰，即在阶梯处反射信号较轴端反射要弱。此外，仿真信号能准确地表现阶梯处反射较弱，随着传播时间越长而能量越来越分散等特性。

3.3 阶梯退刀槽轴实验-仿真

实验中采用的阶梯轴长度为600 mm，轴直径为16 mm，阶梯处位于轴中心，直径为25 mm，宽度为4 mm。退刀槽位于阶梯与轴端正中，深度为1 mm，宽度为2 mm，入射信号频率为300 kHz。

图7(e)为使用DB6小波包进行四层分解产生的(4,1)段波形(取入射信号主要频率所在的频段)。由小波变换之后的实验结果可以比较清晰地分辨出1,2,3,4,5号反射波峰分别与仿真结果(见图7(e))的1,2,3,4,5号波峰在时间间隔与幅值的大小相对应。同时，退刀槽的存在使得信号反射时间越长，传播情况因为波形叠加，频散等原因趋于复杂，实验信号从8号反射波峰之后波形已经无法分辨。

3.4 结果汇总

从光轴、阶梯轴、阶梯退刀槽轴的实验以及仿真可以得出：对于光轴，影响声发射信号最大的因素是轴端的反射；对于阶梯轴，阶梯处的反射、透射、波型转换等因素对波形信号传播影响明显；当退刀槽存在时，其对波形又会有反射、透射影响，同时退刀槽的存在也会加剧波形畸变。

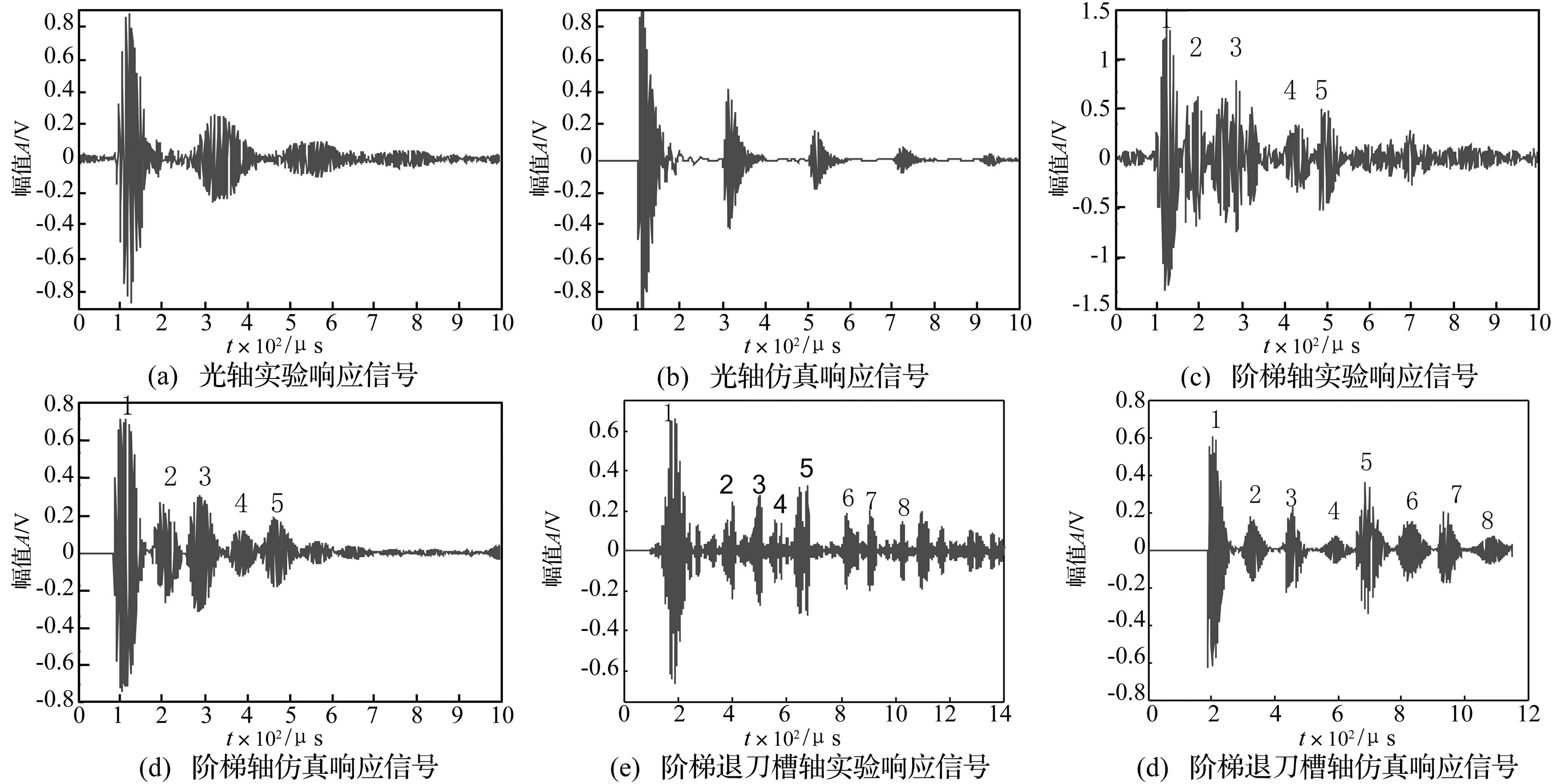
图7 实验-仿真对比

4 结 论

(1)不同结构轴(光轴、阶梯轴、阶梯退刀槽轴)对声发射源信号的影响主要表现反射、透射、衰减、能量逐渐分散等特性。当阶梯界面和退刀槽存在，或者其位置、尺寸改变时，声发射信号反射、透射、衰减、能量分布等特性都会发生可预测的改变。本文中研究的不同轴结构在旋转机械中无处不在，我们在利用声发射技术进行源定位、故障信息提取时应当考虑到这些结构对源信号造成的影响，从而获得更加准确的源故障信息。

(2)有限差分格式是建立声发射信号传播模型的有力方法，其对光轴、阶梯轴、阶梯退刀槽轴的仿真都与实验数据符合度较高，同时其对还原或者反演声发射源信号在轴的传播都将提供重要的理论基础。

参 考 文 献

[1](日)勝山邦久. 声发射(AE)技术的应用[M].北京：冶金工业出版社，1996.2.

[2]沈功田，戴 光，刘时风.中国声发射检测技术进展-学会成立25周年纪念[J]. 无损检测NDT, 2003, 25(6): 302-307.

SHEN Gong-tian，DAI Guang，LIU Shi-feng. Acoustic emission progress in china-celebration for the 25th anniversary of Chinese society for NDT [J]. Nondestructive Testing, NDT, 2003, 25(6): 302-307.

[3]Efstratios M L，Evangelos S D. Acoustic emission source location in dispersive media [J]. Signal Processing, 2007, 87:3218-3225.

[4]龚仁荣，程志勤，顾建祖,等.模态声发射在结构材料缺陷定位中的研究[J]. 振动与冲击，2006，25(3)：176-192.

GONG Ren-rong，CHENG Zhi-qin，GU Jian-zu， et al. Study of fault location in structural material by model acoustic emission [J]. Journal of Vibration and Shock，2006，25(3)：176-192.

[5]卢文秀，褚福磊．基于声发射技术的水轮机故障诊断[J]．振动与冲击，2008，27(s)：291-294．

LU Wen-xiu，CHU Fu-lei. Fault diagnosis in hydro-generator based on acoustic emission[J]. Journal of Vibration and Shock，2008，27(s)：291-294.

[6]何永勇，印欣运，褚福磊. 基于小波尺度谱的转子系统碰摩声发射特性[J]. 机械工程学报，2007，43(6)：149-153.

HE Yong-yong, YIN Xin-yun, CHU Fu-lei. Accoustic emission characteristics of rub-impact for rotor-bearing system based on wavelet scalogram [J]. Journal of Mechanical Engineering，2007，43(6)：149-153.

[7]Flynnt H W，Wood B R A. Acoustic emission pulse path propagation on a cylindrical pressure vessel [R]. Pan Pacific Conference on Non-Destructive Testing，1984.

[8]孙立瑛，李一博，王伟魁,等.突发型声发射信号的传播特性及定位研究[J]. 压力与声光，2001，31(5)：745-748.

SUN Li-ying，LI Yi-bo，WANG Wei-kui, et al. Research on propagation characteristics and location of burst acoustic emission signal traveling along pipeline [J]. Piezoelectectrics & Acoustooptics，2001，31(5)：745-748.

[9]Yih-Hsing P. Theory of acoustic emission [J]. Elastic Waves and Non-Destructive Testing of Materials，1978：107-128.

[10]龚仁荣. 结构材料中声发射传播特性的研究[D].镇江：江苏大学，2005，5

[11]郭福平. 波导杆声发射特性实验研究[D].大连：大庆石油学院，2008.

[12]Glimm J, Marshall G, Plohr B. A generalized Riemann problem for quasi-one-dimensional gas flows[J]. Advances in Applied Mathematics, 1984, 5(1): 1-30.

[13]Hirose S, Achenbach J D. Time-domain boundary element analysis of elastic wave interaction with a crack [J]. International Journal for Numerical Methods in Engineering, 1989, 28(3): 629-644.

[14]Xiao L，Ballmann J. A numerical scheme for axisymmetric elastic waves in solids [J]. Wave Motion，1995,21：115-126.