橡胶轴承-转轴系统碰摩响应动力学特性研究

花纯利， 塔 娜， 饶柱石

(上海交通大学 振动、冲击噪声研究所 机械系统与振动国家重点实验室，上海 200240)

转轴系统广泛用于实际工程。为提高转轴系统机械效率，将转轴与轴承间隙设计的越来越小，但会使转轴系统发生碰摩的可能性提高。转轴与轴承间发生碰摩将致转轴系统局部发热甚至严重磨损，诱发机械剧烈振动，严重时会出现反向涡动失稳造成整个机械系统破坏。因此，研究转轴系统的碰摩复杂非线性动力学行为、确定其与系统参数间关系、揭示系统稳定性边界条件，对优化转轴系统设计与故障诊断意义甚为重要。

对转轴系统碰摩研究已有大量成果。自上世纪80年代以来，在实验、数值模拟、理论分析等方面对转子系统碰摩响应特性进行广泛深入研究。如同频全周碰摩运动、“跳跃”现象[1-6]，准周期局部碰摩运动[7]及混沌行为[8-10]。文献[11-13]中所用模型虽与本文相似，但其接触力为线性模型且未深入讨论偏心率对系统动态特性影响，亦未解释、阐明跳跃现象产生的条件。文献[2]亦用两自由度转子模型，但其定子具有耦合刚度且接触力为线性模型。止今，大部分研究主要集中在将轴承简化为无质量线性弹簧的转轴碰摩模型上，但该简化不能充分反映具有超弹性材料特性的橡胶轴承动态特性。国内外船舶及深井泵等设备中因大量使用橡胶轴承，致使橡胶体磨损严重。此与螺旋桨轴承支承的整个转子系统静态特性与动力响应密切相关。由于对橡胶轴承支撑的转轴/轴承系统研究较少，且对全面考虑碰摩主要参数的非线性弹性支撑的转轴/轴承系统模型动力学特性认识不足，尤其对转轴/轴承偏心率及阻尼比对系统动力响应所致影响了解更少。因此，本文以橡胶轴承支撑的转轴/轴承系统为对象，将其简化为非线性弹性支撑的转轴/轴承系统进行研究，并分析该模型动力学特性。即分析转轴系统发生碰摩、鞍结分叉及Hopf分叉的边界条件，讨论阻尼比与偏心率等系统参数对系统稳定性影响。

1 模型与运动控制方程

橡胶轴承/转轴系统示意图见图1，橡胶轴承由轴承衬套与橡胶衬套两部分组成。将其简化成Jeffcott转子系统，见图2，转轴简化为一支撑在无质量刚度k，阻尼c，转轴中间质量m的刚性转轴上，转轴与轴承间间隙δ，转轴质心与几何中心偏心距e。

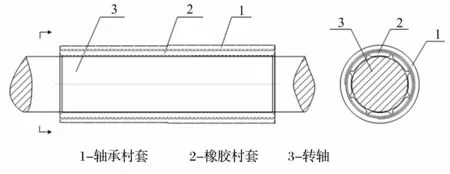
图1 转轴/轴承系统示意图

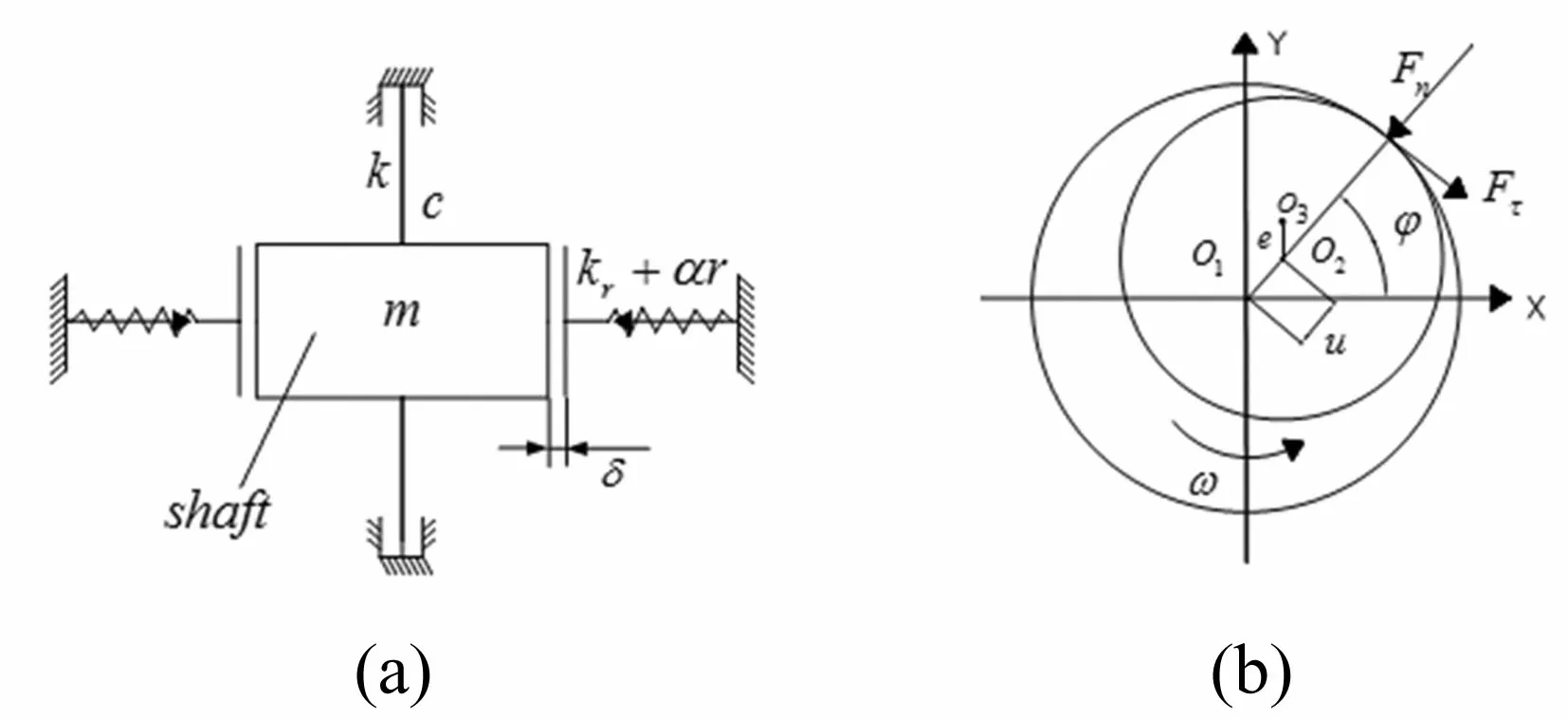
图2 Jeffcott转轴/轴承系统模型

考虑橡胶轴承具有的非线性特征，计入支承刚度的非线性特性。由于轴系的橡胶艉轴承均为新设计产品，未经实验测得准确刚度曲线。因此，其非线性载荷-变形关系参照德国国防军舰艇建造规范(BV043)进行估算：

F=krr(1+100r)=krr+αr2

(1)

其中：F为载荷(N)；r为变形量(m)；kr为轴承刚度值(N/m)。故轴承内环面上转轴/轴承接触刚度为kr+αr。则转轴与轴承间的摩擦力及接触力为：

(2)

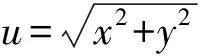
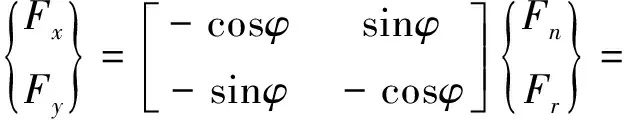
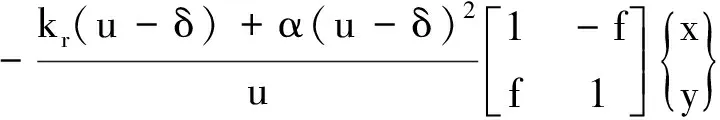
(3)

橡胶轴承/转轴系统动力学方程可表达为：

(4)

式中：Θ为heaveside函数，即：

将橡胶轴承/转轴系统动力学方程无量纲化：

(5)

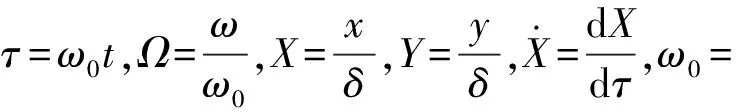
转轴旋转过程中，转轴与轴承接触、不接触状态均有稳定的周期解。设其解的形式为：

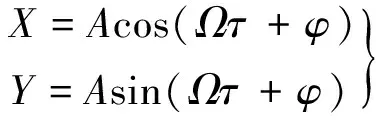
(6)

在轴承与转轴未发生接触状态下Θ=0，将式(6)代入控制方程并求解得幅值、相位角分别为：

(7)

由于轴承与转轴间隙有限，故非接触状态下所求幅值A须满足A≤1条件。即：

(ρ2-1)Ω4+2(β-2ξ2)Ω2-β2≤0

(8)

通过求解式(8)可两实根Ωl，Ωu，且记为线性转轴开始发生碰摩时低、高转速。当Ω<Ωl或Ω>Ωu时，转轴系统存在无碰摩同频周期响应。

轴承与转轴发生接触状态下Θ=1，将式(6)代入式(5)得关于振动幅值A的方程式：

a4A4+a3A3+a2A2+a1A+a0=0

(9)

其中：

a4=g2+g2f2

a3=2g[(1-2g+β-Ω2)+f(2ξΩ+f-2gf)]

a2=(1-2g+β-Ω2)2+(2ξΩ+f-2gf)2+

2g(g-1)(1+f2)

a1=2(g-1)[(1-2g+β-Ω2)+f(2ξΩ+f-2gf)]

a0=(g-1)2(1+f2)-ρ2Ω4。

一元四次方程最多有两个互异的正实数根，复数与负数实根均无实际意义。在式(5)Θ=1条件下，方程有二重正实根时，即为系统鞍结分叉的边界条件。为保证轴承与转轴处于接触状态，幅值A不仅需满足正实数条件且需满足幅值A>1。

2 周期解稳定性分析

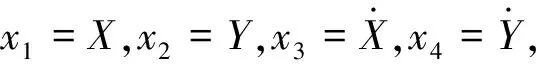
(10)

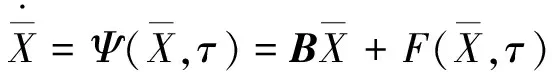
(11)

式中：

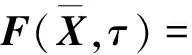
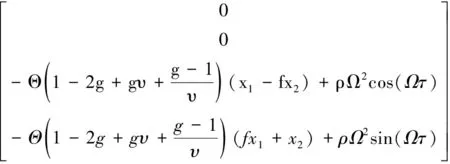
为简便，引入稳态周期解形式：

(12)

其中：A为非接触状态下式(7)与接触状态下式(9)的稳定周期解。

通过解式(11)得：

(13)

当Θ=0时转轴与轴承处于非接触状态，雅可比方程J恰好是矩阵B，对应的特征方程为|B-λI|=0，将其展开：

λ4+4ξλ3+(2β+4ξ2)λ2+4ξβλ+β2=0

(14)

根据Routh-Hurwitz(劳斯-霍尔维茨)稳定性判据，式(5)(Θ=0时)非接触状态解的稳定性条件为：

ξ>0

(15)

由式(15)知，当系统阻尼为正阻尼时，对应的周期解是稳定的。当系统振动幅值大于间隙δ时，轴承与转轴会发生碰摩。此时转轴系统控制方程中Θ=1。式(5)的解将为非线性的周期解。其雅可比矩阵J可表达为：

(16)

式中：

由式(16)知，雅可比矩阵J为周期性的时间依赖矩阵，不能直接推导、分析其解的稳定性，需作变换：

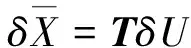
(17)

式中：转换矩阵T为：

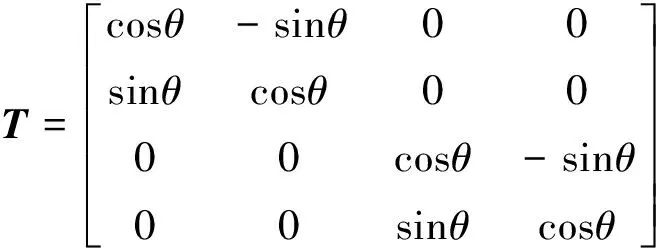
将式(17)代入式(13)，得：

(18)

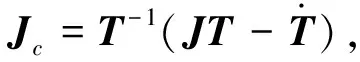
(19)

式(19)表明雅可比矩阵Jc与时间参数无关。δU解与式(11)解的稳定性取决于矩阵Jc特征值实部符号。对应的特征方程满足|Jc-λI|=0，将其展开为：

b4λ4+b3λ3+b2λ2+b1λ+b0=0

(20)

其中：

b4=1

b3=4ξ

诸多系数均为幅值A的函数，故Routh-Hurwitz(劳斯-霍尔维茨)稳定性判据可用于判断式(11)非线性稳态周期解的稳定性。

基于分叉理论,分析周期解的分叉边界，给出参数空间稳定区域。若雅可比矩阵Jc有一零特征值，系统将出现鞍结分叉，此时式(20)中b0=0，即：

(21)

通过消除幅值A的符号计算，同时求解式(9)、(21)获得关于Ω的12次多项式。求解参数方程，可得式(9)发生鞍结分叉条件的参数空间。全周碰摩解的鞍结分叉点处幅值A为大于1的正实数。

基于Hopf分叉理论，系统会有一对共轭纯虚数特征值。将λ=+iωυ代入式(20)得：

(22)

消去参数ωυ得(代入λ=-iωυ得同样结果)：

(23)

需满足不等式：

b1/b3>0

(24)

用式(9)、(23)消去幅值A，求解参数方程，可得系统发生Hopf分叉的边界线HF。同频全周碰摩解Hopf分叉点处幅值A为大于1的正实数。

3 系统参数对转轴响应影响

由式(15)知，转轴系统在无碰摩状态下周期解总是稳定的，但转轴与轴承间间隙有限，因此周期解不可能在系统的所有参数下一直存在。由式(8)及分析知，线性橡胶轴承/转轴系统激振频率分别由高、低转速趋向系统固有频率时，系统振动幅值A会在Ω=Ωl与Ω=Ωu处趋近1。当转轴/轴承系统处于接触状态、激振频率分别向低、高转速变化时，系统振动幅值A会在Ω=SNl与Ω=SNu处趋近1。由式(9)、(21)知，碰摩状态存在于转速SNl与SNu之间，SNl与Ωl基本相等，SNu与Ωu或相等或不等，取决于系统参数，两者不等时系统振动幅值将随转速的变化出现跳跃现象。如将曲线Ω=Ωl，Ω=Ωu，Ω=SNl，Ω=SNu，Hopf分叉边界HF绘制于(Ω,ξ)平面，则该平面将被分隔成若干部分，不同部分代表系统不同运动状态，即(A)，(B)为无碰摩周期运动；(C)为同频全周碰摩运动；(D)为局部碰摩运动及反向涡动失稳运动；(E)为无碰摩周期运动及同频全周碰摩运动共存，即处于接触状态条件下系统做同频全周碰摩运动，而处于非接触状态条件下系统做无碰摩周期运动；(F)为无碰摩周期运动、局部碰摩运动或反向涡动失稳运动，即处于接触状态条件下系统做局部碰摩运动或反向涡动失稳运动，而处于非接触状态条件下系统做无碰摩周期运动。

对不同参数取值下系统运动状态演变过程分别进行讨论。取偏心率ρ=0.8，系统各参数分别为：f=0.2,β=0.5，g=0.01。此时曲线Ω=Ωl，Ω=Ωu，Ω=SNl，Ω=SNu，分叉边界HF将(Ω,ξ)平面分成四部分，转轴系统在转速Ω，阻尼比ξ参数平面内系统响应特性区域见图3。因Ωl=SNl，Ωu=SNu，系统不会发生跳跃现象。由图3知，在区域(C)内转轴系统做同频全周碰摩运动，在区域(D)内系统做非稳定周期碰摩运动。

将系统偏心率减小为ρ=0.5时，转轴系统响应稳定区域发生明显变化，见图4。

与偏心率ρ=0.8情况相比，系统响应特性在(Ω,ξ)平面内发生显著变化，边界Ω=Ωl=SNl向右移动，边界Ω=Ωu与Ω=SNu向左移动，且曲线Ωu，SNu不重合。Hopf分叉边界线HF无明显变化。因此，非稳定碰摩响应区域(D)及同频全周碰摩运动区域(C)的两侧边界向中间靠拢而缩小，表明系统出现全周碰摩转速范围变小；出现同频全周碰摩运动与无碰摩周期运动共存区域(E)及无碰摩周期运动、局部碰摩运动或反向涡动失稳运动区域(F)。此时转轴系统同频全周碰摩运动会存在于Ω=Ωl与Ω=SNu区间内；区间Ω>Ωu存在无碰摩周期运动，故在区间Ωu，SNu间同频全周碰摩运动与无碰摩周期运动均可能存在。当转轴系统转速Ω发生变化时会有跳跃现象发生。

由讨论可知，偏心率降低会使碰摩区域发生明显变化并出现跳跃现象，因此，需进一步讨论其对转轴系统响应影响。转轴系统在(Ω,ρ)平面的响应特性见图5。

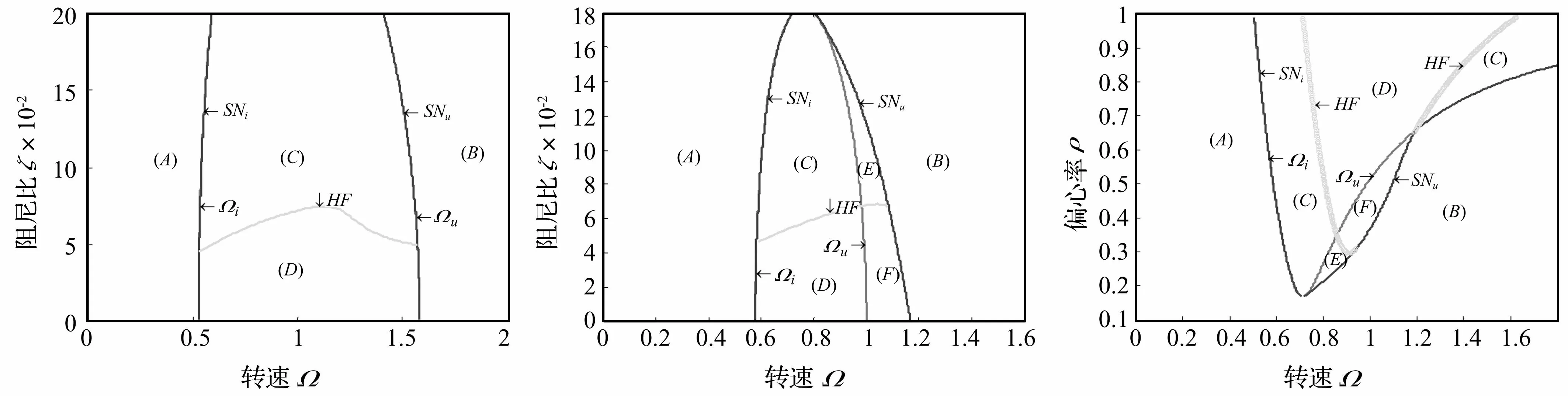
图3 转轴碰摩响应在(Ω, ξ)平面稳定区域图(ρ=0.8)

由式(8)所得Ωu，Ωl值可给出转轴与轴承由无接触向接触过渡时临界转速上、下边界。由图5看出，①系统共振振幅小于转轴与轴承间间隙即ρ<0.17时，转轴与轴承间不发生碰摩；随偏心率的增加Ωl逐渐减小而Ωu却逐渐增大，因此Ωl与Ωu间区域增大，即发生碰摩的转速区间增大。②同理可得转轴与轴承由接触状态向脱离接触状态过渡时转速的上、下边界值SNu及SNl，而Ωl与SNl总相等；Ωu与SNu在0.17<ρ<0.65范围内不相等，该区域内转轴系统振幅随转速的变化会发生跳跃现象，且随偏心率的增加发生跳跃现象的转速区间呈现先增大后减小直至消失的趋势；③由于转轴系统Hopf分叉边界HF与鞍结分叉边界SNu在ρ=0.3处相交一点，ρ>0.3时，随偏心率的增加，开始发生Hopf分叉的转速Ω逐渐减小，导致落在区域(E)内的转速区间不断缩小并最终消失；0.17<ρ<0.3时，系统不会出现Hopf分叉及失稳现象，只会出现无碰摩周期运动、同频全周碰摩运动或两运动状态跳跃转变现象。

4 结 论

本文对轴承简化为非线性弹性支撑转轴系统发生周期无碰摩运动与同频全周碰摩运动存在的区域及稳定性进行研究，并分析阻尼比及偏心率等系统参数对转轴系统动态特性影响、对不同转轴系统响应特性边界条件影响。结论如下：

(1)转轴系统Hopf分叉边界HF为转速、摩擦系数、阻尼比及偏心率的函数。Hopf分叉边界将碰摩响应区域划分成同频全周碰摩响应区域与局部碰摩运动、反向涡动失稳运动区域两部分。

(2)阻尼比是影响转轴碰摩响应的主要参数之一。大阻尼比系数下，转轴系统响应主要为无碰摩周期运动、同频全周碰摩运动及两种响应共存；小阻尼比系数会出现不稳定碰摩运动。因此，大阻尼比转轴系统更稳定。

(3)偏心率是转轴系统重要参数之一，偏心率小转轴系统稳定。偏心率小至转轴系统共振幅值小于间隙时，转轴与轴承间不发生碰摩。随偏心率的增加转轴与轴承会在某状态下发生碰摩；小偏心率时，系统有周期无碰摩运动及同频全周碰摩运动且会发生在两运动状态间跳跃现象，较大偏心时系统会在某转速下发生Hopf分叉,且随偏心率的增大,发生Hopf分叉所需转速会降低。

参 考 文 献

[1]Ehrich F F. High order sub-harmonic response of high speed rotors in bearing clearance[J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1988, 110: 9-16.

[2]Jiang J,Ulbrich H. Stability analysis of sliding whirl in a nonlinear jeffcott rotor with cross-coupling stiffness coefficients[J]. Nonlinear Dynamics,2001,24(3):269-283.

[3]Zhang H B, Chen Y S, Li J. Bifurcation on synchronous full annular rub of rigid-rotor elastic-support system[J]. Applied Mathematics and Mechanics,2012,33(7):865-880.

[4]Zhang H B, Chen Y S. Bifurcation analysis on full annular rub of a nonlinear rotor system [J]. Science China Technological Sciences, 2011, 54(8): 1977-1985.

[5]Shang Z Y, Jiang J, Hong L. The global responses characteristics of a rotor/stator rubbing system with dry friction effects [J]. Journal of Sound and Vibration, 2011, 330(10) :2150-2160.

[6]李朝峰，戴继双，闻邦椿. 油膜支撑双盘转子-轴承系统周期运动稳定性与分岔[J]. 力学学报,2011,43(1):208-216.

LI Chao-feng, DAI Ji-shuang, WEN Bang-chun. Stability and bifurcation of the rotor-bearing system with double disks supported by cylindrical bearings[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1):208-216.

[7]Kim Y B, Noah S T. Quasi-periodic response and stability analysis for a nonlinear jeffcott rotor[J]. Journal of Sound and Vibration, 1996, 190(2): 239-253.

[8]Goldman P, Muszynska A. Chaotic behavior of rotor/stator system with rubs[J]. Journal of Engineering for Gas Turbines and Power, 1994, 116: 693-701.

[9]Evgueni V K, Wiercigroch M, Cartmell M P. Regular and chaotic dynamics of a discontinuously nonlinear rotor system[J]. Chaos,Solitons and Fractals,2002,13(6): 1231-1242.

[10]褚福磊, 张正松, 冯冠平. 碰摩转子系统的混沌特[J]. 清华大学学报( 自然科学版),1996,36(7):52-57.

CHU Fu-lei, ZHANG Zheng-song, FENG Guan-ping. Chaotic behavior of a rub rotor model[J]. Journal of Tsinghua University ( Sci & Tech), 1996,36(7):52-57.

[11]刘 林, 江 俊. 转子/定子碰摩响应的全局动力学特性研究[J]. 应用力学学报,2006, 23(3):351-356.

LIU Lin, JIANG Jun. Global dynamical characteristics of rotor/ stator rubbing [J]. Chinese Journal of Applied Mechanics, 2006, 23(3):351-356.

[12]Zhang W M, Meng G. Nonlinear dynamics of a rub-impact micro-rotor system with scale-dependent friction model [J]. Journal of Sound and Vibration, 2008, 309(3-5): 756-777.

[13]张义民, 刘巧伶, 闻邦椿. 旋转机械系统碰摩故障的失效灵敏度研究[J]. 振动工程学报,2007,20(2):189-193.

ZHANG Yi-min, LIU Qiao-ling , WEN Bang-chun. Failure sensitivity investigation in impact-rub malfunction for rotating machinery[J].Journal of Vibration Engineering,2007, 20(2):189-193.