结构多轴抗震试验加载系统开发及控制策略研究

曾 聪， 吴 斌， 许国山， 陈永盛

(1.哈尔滨工业大学 土木工程学院，哈尔滨 150090；2.东北电力大学 建筑工程学院，吉林 132012)

地震对结构的作用通常为多轴的，且为持续变化的。为估计结构的地震反应，试验系统亦日趋复杂化、精细化。随结构动力试验技术深入研究及液压伺服系统快速发展，用多自由度加载系统对结构或构件进行多维动力试验愈受关注。图1为在NEES计划(Network for Earthquake Engineering Simulation)资助下美国建成的两具备多轴加载能力的六自由度混合试验系统。即MAST加载系统[1]与MUST-SIM加载系统[2]。但六自由度加载系统因其投资巨大、控制复杂未得到广泛应用。Shing等[3]建立的两自由度加载系统以模拟柱顶弯矩、剪力，对钢结构立柱进行拟动力试验，但未考虑轴力。Shoraka等[4]对混凝土立柱进行混合试验，用三自由度加载系统模拟柱顶轴力、弯矩、剪力的复杂边界条件。但试验结果是作动器间耦合效应显著，试验系统控制效果不理想。国内对多轴动力试验加载系统研究基本处于空白，因此该研究对我国结构动力试验技术、手段的发展与进步具有重要意义。

图1 六自由度结构动力试验加载系统

建立多功能、高性能的多自由度结构动力试验系统，将其应用于结构动力试验，仍面临诸多困难。

(1) 在传统的拟静力试验中，竖向加载往往通过千斤顶实现，而千斤顶的力控制为开环，与采用反馈控制作动器相比，控制精度低得多(尤其试件进入非线性后)。在水平荷载干扰下，竖向力较难保持恒定。因此，需研究采用液压伺服作动器作为竖向加载设备试验方法。

(2) 结构动力试验中试件刚度进入下降段时，若作动器采用单环反馈力控制加载，为实现目标力，作动器冲程会迅速加大，易使试件快速溃塌，对作动器及试验设备(如传感器)造成伤害，甚至会危及试验人员安全。如何使作动器在位移控制加载情况下实现力的控制目标非常值得研究。

(3) 多自由度加载系统由多个液压伺服作动器组成并联机械系统，对应各自由度命令及各作动器命令间存在整体坐标系与作动器局部坐标系间转换。此外，进行多自由度大比例尺结构试验时，试件刚度大，会增加多作动器间耦合效应。如何准确模拟试件复杂的边界条件，采用何种数值积分方法进行混合试验，如何实现多作动器的协调加载等均为建立混合试验系统须考虑、解决的问题。

为此，本文开发出三自由度结构动力试验加载系统，对拟静力试验与混合试验的控制策略及试验方法进行研究，并应用于足尺钢结构立柱的动力试验中。

1 三自由度结构动力试验加载系统开发

完整的试验系统由试验端、控制端两部分构成。

1.1 加载系统试验端构成

该加载系统试验端由3台MTS公司的阀控电液伺服作动器(最大出力1 000 kN，最大行程±250 mm)与自行加工设计的加载分配梁、3块作动器与反力台座的连接板、平面外的侧向支撑(滚轮)与支撑框架、试件及垫板、螺栓等构成。试件、加载系统具体尺寸见图2，安装后三自由度加载系统照片见图3。该加载系统试验端安装顺序应为：水平作动器就位→试件就位→加载梁吊装并与试件和水平作动器连接→竖向作动器吊装并连接(先连下端，后连上端)→侧向支撑框架就位→侧向支撑安装。尤其强调两点：① 因作动器长度在一确定范围内，故需据试件高度调整垫板厚度以保证加载系统尺寸精度，避免初始应力；② 侧向支撑刚度对保证加载系统平面外稳定至关重要，设计时需备足刚度，安装时需顶紧。

图2 三自由度结构动力试验加载系统构造图

图3 三自由度结构动力试验加载系统

1.2 加载系统的控制端构成

该加载系统控制端可有多种组合。用MTS液压伺服系统的MTS793.10控制软件及Flextest GT控制器组合较简单易行，可使数值计算与试验控制在同一台计算机中完成。

MTS793.10软件对试验系统的控制可通过对站(Station)的操作实现[5]。总体分两部分，即建立站(Station Builder)与管理站(Station Manager)。据已有硬件设备及试验安排建立试验站后，可用站管理器对试验进行管理、操作。而Station Manager中计算编辑器模块(Calculation Editor)与多目标试验模块(MPT)在多自由度动力试验中极为重要。建站时建立计算通道后可用简单脚本语言在计算编辑器中编写计算程序[6]，该程序或是复杂的控制方法(混合控制方法)，或是混合试验中数值子结构积分计算(α-OS法)，再通过MPT模块运行计算程序。

上述方法缺陷在于MTS793.10中的计算编辑器模块编程能力有限，不支持矩阵运算及内部循环。进行混合试验、数值子结构较复杂需计算的自由度个数较多时，用计算编辑器编写计算程序会较困难。但MTS伺服系统能提供外部数字及模拟信号输入输出端口，因此，用数值计算软件(如Matlab, Opensees等)+试验协调软件(OpenFrasco等)+实时仿真平台(dSPACE等)+控制器(Flextest GT)构成控制端方法可行[7-9]。

2 拟静力试验混合控制方法研究

用三自由度加载系统进行拟静力试验的控制目标在拟静力试验过程中使试件所受竖向力始终保持恒定，分配梁始终保持水平(即剪切型加载)。即在水平作动器干扰下，使两竖向作动器出力之和在试验过程中保持恒定，且两竖向作动器位移始终保持一致。

此控制目标似乎既要实现对力的控制，也要实现对位移的控制，而传统的单环反馈控制则不可能实现。为此，本文提出采用双环反馈的混合控制方法，基于该方法提出多个竖向作动器在拟静力试验中的耦合控制策略。

2.1 双环反馈混合控制方法

该方法控制框图见图4。系统控制目标力fi+1与作动器力传感器采集的力fi+1’进行比较，获得力的误差信号ef(t)，通过力-位移转换系数CF将经外环力控制器调节后的力误差信号转换为作动器位移命令di+1(t)，作动器通过内环反馈实现位移命令，力位移转换系数可取试件初始刚度的倒数。

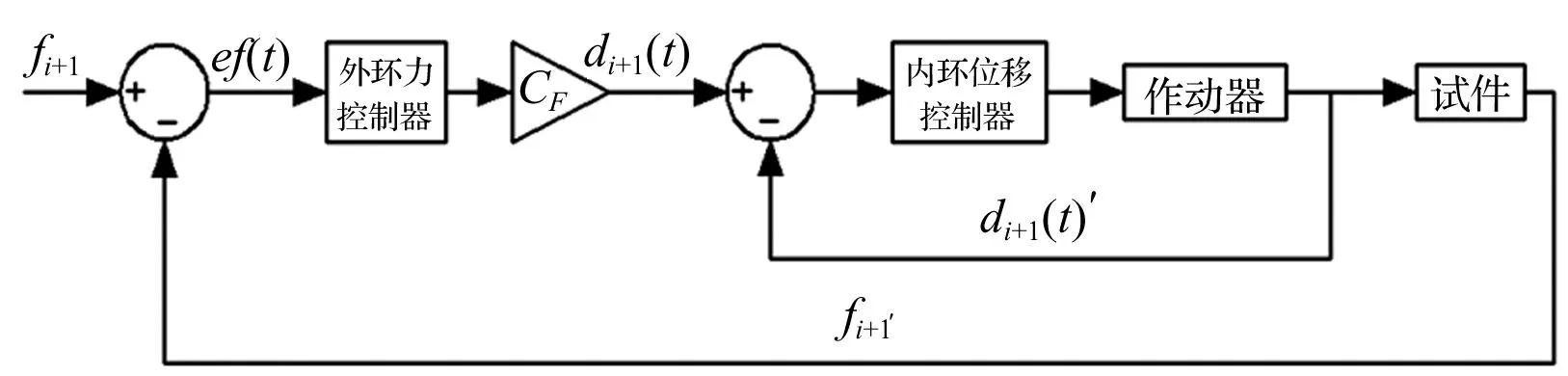
图4 用双环反馈的混合控制框图

该混合控制方法能实现作动器在力控制下的位移加载，能克服力控制加载缺点，对力控制的刚度衰减型试件加载控制效果较好。研究表明，该方法的控制效果对CF变化不敏感，说明该控制方法具有较好的鲁棒性。

2.2 拟静力试验竖向作动器耦合控制方法

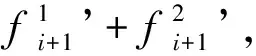
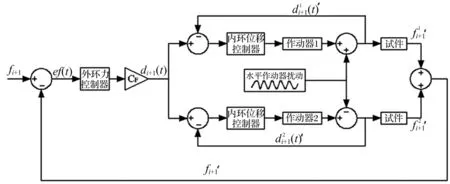
图5 拟静力试验竖向作动器耦合控制框图

由此知，该耦合控制策略通过外环反馈可实现合力命令，通过内环反馈可实现一致位移加载，即最终实现拟静力试验加载控制目标。

3 基于α-OS法的混合试验方法

α-OS法由Nakashima等[10]提出，可用于混合试验的数值积分算法。由于α法的时间步长Δt取值与结构振型最高频率成反比，结构复杂、高阶振型最高频率较大时Δt取小值，该方法会失效。而α-OS法则将结构刚度人为划分成线性刚度、非线性刚度两部分，将OS法中显式预测修正方法引入α法中，使该方法能兼具α法与OS法优点，最终实现无需迭代且无条件稳定的α-OS法。该方法具体计算步骤见图6。

图6 α-OS法计算步骤

图6中参数意义、取值方法为：本文试验取积分步长Δt=0.02 s；M，C，KI分别为整个结构(包括数值子结构及试验子结构)质量矩阵、阻尼矩阵及初始刚度矩阵。α取值范围[-1/3,0]，本文试验取α=-1/6，β=(1-α)2/4，γ=(1-2α)/2；向量d，v，a，f，r分别表示位移、速度、加速度、地震力、恢复力。下标n，n+1表示积分步数，上标m表示测量值。符号顶部“^”表示虚拟质量或虚拟地震力为数学表达式，无实际物理意义。符号顶部“～”表示该值为估计值。用α-OS法进行混合试验步骤清晰、计算简单，由于采用预测修正步骤，即使试件进入非线性，仍能较好完成混合试验。

4 试验验证

本文以足尺钢结构立柱为试件。通过单步阶跃输入及正弦输入测试双环反馈混合控制方法的控制效果，进行拟静力试验，验证基于力控制下位移加载的竖向作动器耦合控制在拟静力试验中的控制效果。基于α-OS方法通过本文开发的三自由度加载系统对单柱子结构进行混合试验。

4.1 采用双环反馈的混合控制效果

在双环反馈控制中，控制器(尤其外环控制器)的设计是关键，因此需对整个试验系统进行数学建模，通过数值仿真完成控制器初步设计后方可进行试验。简单起见，系统内、外环控制器均采用PI控制，考虑试件特性对作动器影响，获得阀控液压伺服作动器控制信号(差动电流i)及测量位移(dm)间开环传递函数为[11]：

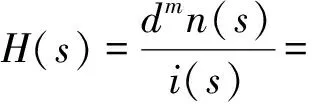
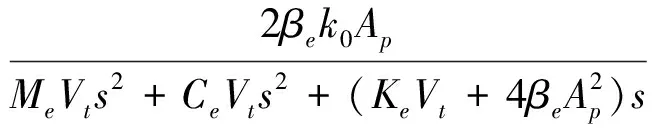
(1)

参数物理意义及取值见表1。设差动电流i与外环力命令成线性关系，由图4、式(1)获得控制系统闭环传递函数，由劳斯判据可证明该控制系统是稳定的[12]。

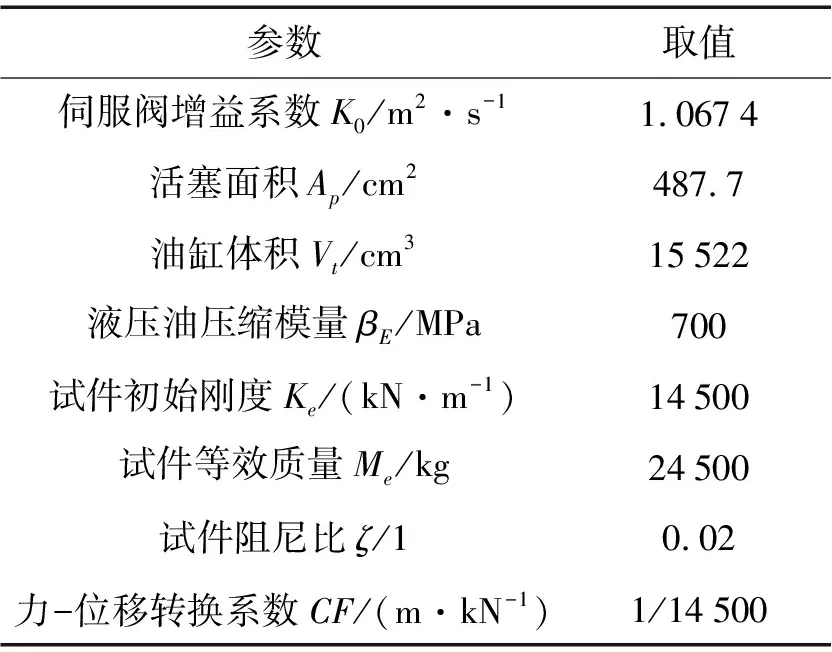
表1 混合控制方法验证试验参数物理意义及取值

用MATLAB进行数值仿真，通过优化调整控制器参数，确定PI控制器参数为：外环力控制器KP=0.05，KI=2；内环位移控制器KP=5，KI=0.5。仿真完成后用水平作动器对足尺钢结构立柱试件进行单步阶跃输入及正弦输入试验，仿真、试验结果见图7。

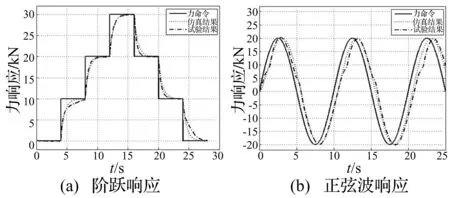
图7 混合控制仿真及试验效果对比

由试验结果看出，通过双环反馈混合控制，作动器力响应可准确实现力命令。但响应速度偏慢，且存在0.5 s时滞。而在慢速试验中(如拟静力试验)此缺陷不影响系统控制效果。若将该控制方法用于快速或实时试验，可通过优化外环控制器设计(如使用滑动模态控制器)加快响应速度或引入前馈补偿消除系统时滞。

4.2 拟静力试验

用三自由度加载系统进行足尺立柱拟静力试验时，对两竖向作动器用耦合控制策略进行控制，竖向目标力为100 kN。为体现耦合控制的鲁棒性，水平作动器用幅值50 kN、加载频率0.1 Hz的正弦波进行往复加载。竖向作动器外环、内环仍用PI控制器进行控制，控制器参数为：外环力控制器KP=0.05，KI=2；内环位移控制器KP=0.5，KI=0.01。试验结果见图8。

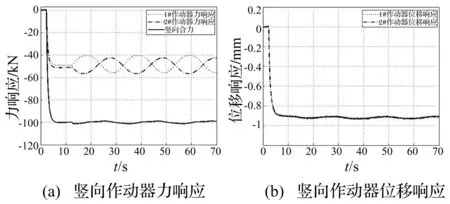
图8 拟静力试验结果

由图8(a)看出，在水平作动器强烈干扰下(水平作动器加载速度较快，幅值较大)，两竖向作动器的力响应始终发生变化，变化幅值接近20%。但经耦合控制，其合力始终稳定在100 kN附近，最大变化仅1.2%，可见对试件恒定的竖向力控制可以实现。由图8(b)看出，两竖向作动器试验过程中的位移变化始终一致，即加载分配梁可保持水平，可实现对试件的剪切型加载。

4.3 混合试验

为验证三自由度加载系统进行混合试验的能力与多作动器协调加载效果，进行平面足尺钢结构框架混合试验。整体结构为高3.3 m，跨度6 m的平面钢结构框架，取其中1根柱为试验子结构，其它部分为数值子结构，用三自由度加载系统模拟试验子结构边界条件，数值子结构采用MTS793.10中计算编辑器基于α-OS积分算法进行编程积分计算，具体试验设置见图9。整个框架质量集中于两个梁柱节点，结构共6个动力自由度，其中试验子结构边界条件为3个动力自由度。地震激励选El Centro地震记录，地震记录峰值取35 gal(七度多遇)。

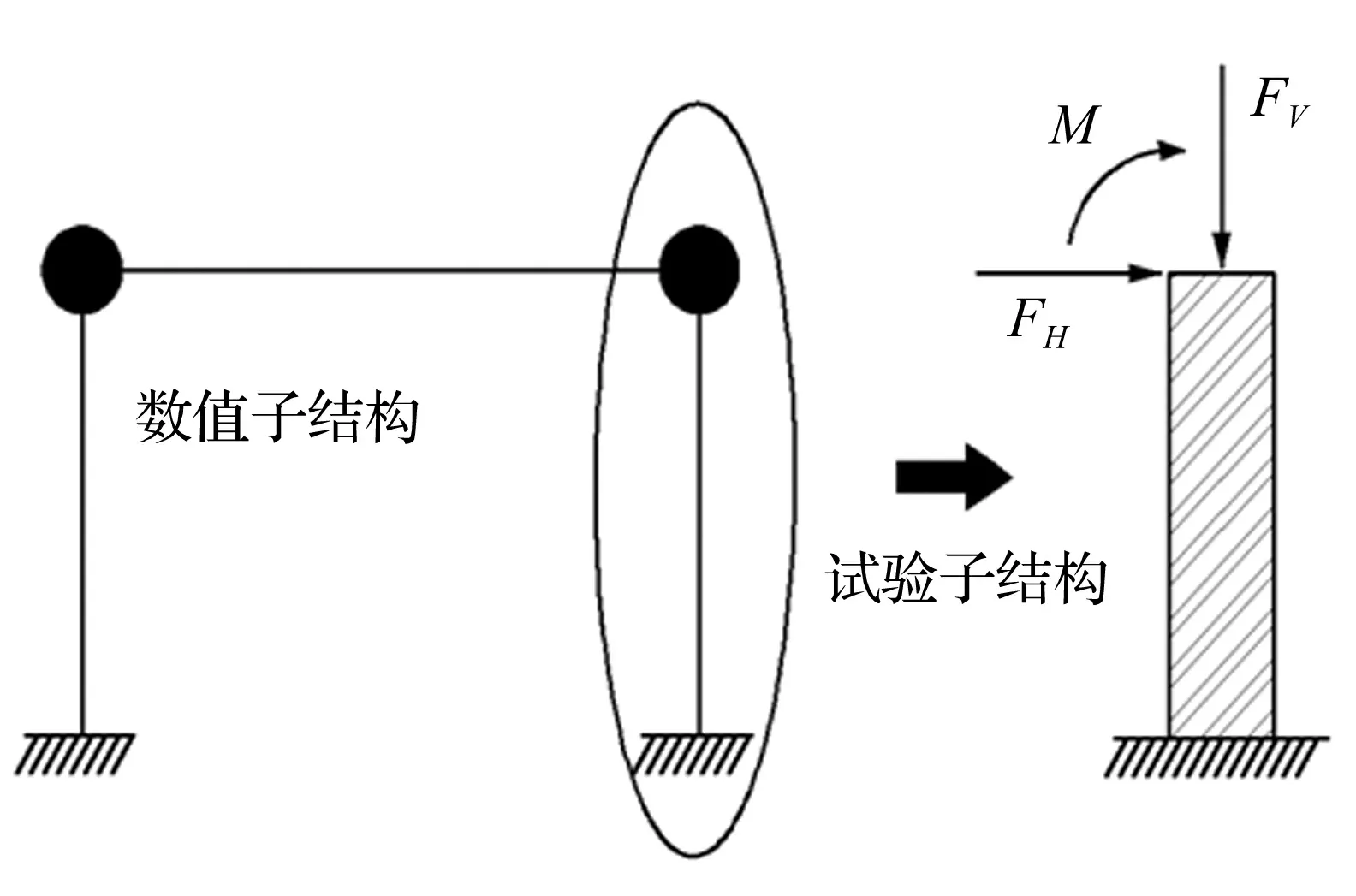
图9 混合试验设置示意图

在基于α-OS法的混合试验积分计算中用质量矩阵、刚度矩阵为：

(2)

(3)

将整个试验系统在平面内的笛卡尔坐标系定义为整体坐标系，将各作动器轴向伸缩定义为局部坐标系。由机械运动学角度，三自由度加载系统为并联机构，欲获得作动器局部坐标下位移命令，需将试件在整体坐标下各自由度命令通过加载系统整体坐标系向作动器局部坐标系变换。设加载系统与试件连接点为并联机构末端，则问题转化为已知末端位姿，求解输入端位姿问题，即求解该系统的运动学反解。

一般并联机构中，需考虑连接副对系统位姿影响，而本试验系统中，整体变形较小，连接头与作动器相比长度较小，因此连接副影响可忽略不计。试验系统坐标系转换见图10。

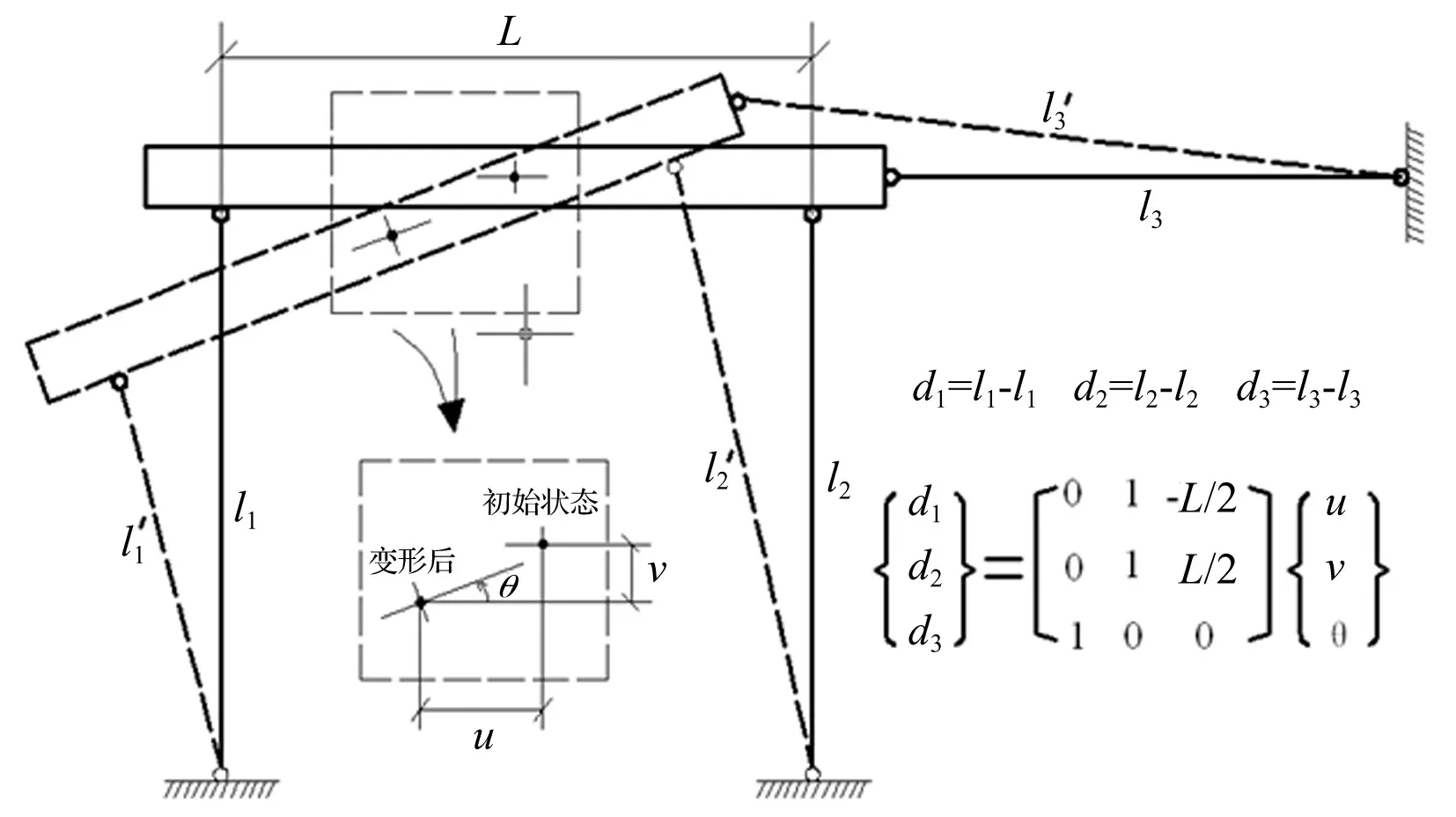
图10 三自由度加载系统坐标变换示意图

图10中d1，d2，d3分别对应3个作动器位移命令，u，v，θ表示由数值计算所得对应于柱顶水平、竖向、转动自由度位移。

足尺立柱试件各自由度混合试验结果见图11。该结果由3个作动器位移响应通过求解试验系统运动学正解获得。由试验结果看，慢速加载时(混合试验时间比取10∶1)各自由度位移响应同步性较好，故该三自由度加载系统可实现复杂边界条件的多作动器位移协调加载，且水平位移仿真结果与试验结果吻合较好，证实用该试验系统可成功进行混合试验。

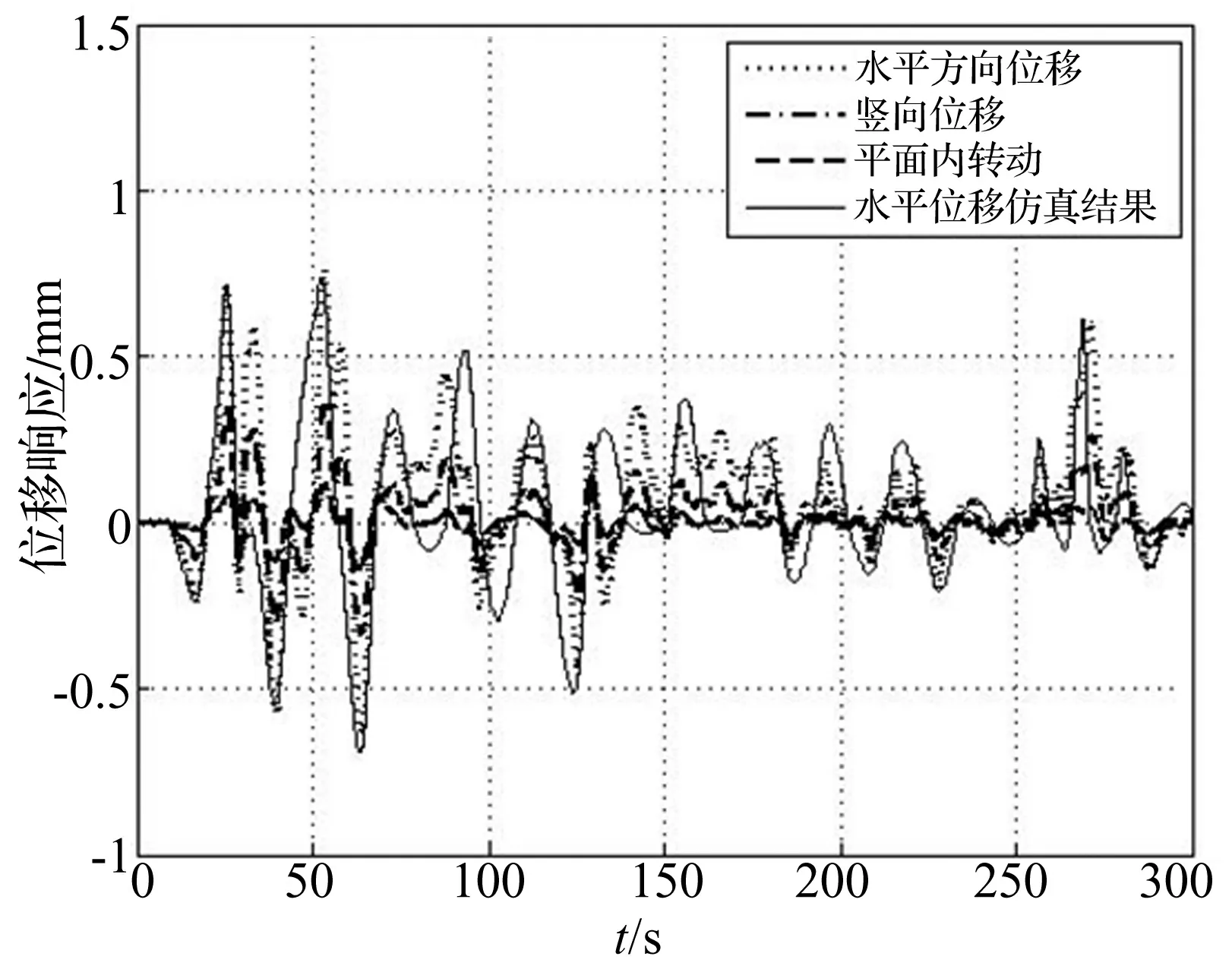
图11 三自由度混合试验各自由度位移响应结果

5 结 论

(1) 本文由试验系统试验端与控制端构建、与试验系统功能相适应的控制策略研究及针对混合试验系统数值积分算法选用入手，开发出基于MTS阀控电液伺服作动器及相应配套控制软件的三自由度结构动力试验加载系统，并针对其两主要功能(拟静力试验与混合试验)提出多作动器力控制的位移加载拟静力试验耦合控制策略及基于α-OS法与坐标系转换的混合试验方法。

(2) 通过试验证明，三自由度加载系统为具备多功能、高性能的先进结构动力试验系统。

参 考 文 献

[1]Catherine W F, Arturo E S. Multi-axial subassemblage testing (mast) system: description and capabilities[R]. The 13th World Conference on Earthquake Engineering, Canada,2004.

[2]Narutoshi N, Billie F S. Multi-dimensional hybrid simulation using a six-actuator self-reaction loading system[R].The 14th World Conference on Earthquake Engineering, China, 2008.

[3]Shing P B, Vannan M T, Carter E W. Implicit time integration for pseudo-dynamic test[J]. Earthquake Engineering and Structural Dynamics, 1991, 20(6):551-571.

[4]Shoraka M B, Charlet A Y. Hybrid simulation of the gravity load collapse of reinforced concrete frames[R]. 18th Analysis and Computation Specialty Conference, 2008.

[5]Model 793.00 system software, user information and software reference[M]. MTS Systems Corporation, 2001.

[6]王大鹏, 张洪涛, 田石柱,等. 基于MTS 计算命令控制的试验系统[J]. 建筑科学与工程学报，2007,24(1):12-16.

WANG Da-peng, ZHANG Hong-tao, TIAN Shi-zhu, et al. Testing system based on calculation command control of MTS [J]. Journal of Architecture and Civil Engineering, 2007, 24(1): 12-16.

[7]王 强，冯 帆，Shawn Y，等.基于有限元软件的子结构拟动力试验技术[J]. 沈阳建筑大学学报(自然科学版)，2010, 26(6):1085-1089.

WANG Qiang, FENG Fan, Shawn Y, et al. Pseudo-dynamic test method with sub-structure technique based on finite element software opensees [J]. Journal of Shenyang Jianzhu University ( Natural Science), 2010,26(6):1085-1089.

[8]周惠蒙，王 涛，陈永盛，等. 采用dSPACE控制的电液伺服试验加载系统[J]. 结构工程师, 2011,27(S1):1-5.

ZHOU Hui-meng, WANG Tao, CHEN Yong-sheng, et al. Electro hydraulic servo experimental loading system with dSPACE control [J]. Structural Engineers, 2011,27(S1):1-5.

[9]陈永盛，吴 斌，许国山，等. 基于OpenFresco-MTS的混合试验系统[A].第三届土木工程结构试验与检测技术暨结构实验教学研讨会, 哈尔滨，2012.

[10]Nakashima M, Akazawa T, Sakaguchi O. Integration method capable of controlling experimental error growth in substructure pseudo dynamic test[J]. AIJ J. of Struct. Constr. Engng., 1993, 454: 61-71.

[11]吴 斌，尹全林，张 涛. 实时子结构试验中加载系统数值模型[J]. 哈尔滨工业大学学报, 2010,42(12):1855-1859.

WU Bin, YIN Quan-lin, ZHANG Tao. Numerical model of loading system for real-time substructure testing [J]. Journal of Harbin Institute of Technology, 2010,42(12):1855-1859.

[12]谭晓晶，吴 斌. 外环位移控制与内环力控制拟动力试验方法[J]. 振动与冲击,2012,31(14):16-21.

TAN Xiao-jing, WU Bin. Pseudo-dynamic testing with control technique combining disp. outer loop and force inner loop[J]. Journal of Vibration and Shock, 2012,31(14):16-21.