基于遗传算法的圆柱空腔吸声覆盖层参数优化研究

陶 猛， 赵 阳， 王广玮

(1.贵州大学 机械工程学院，贵阳 550025；2.上海交通大学 机械系统与振动国家重点实验室, 上海 200240)

在水下航行器表面敷设吸声覆盖层既可减小主动声呐探测回波，亦可降低自身噪声的外辐射，作为提高水下航行器隐身性能的技术手段被广泛采用。经半个多世纪发展，吸声覆盖层研究已取得丰富成果，如共振空腔吸声覆盖层[1-3]、微粒复合吸声覆盖层[4-6]、夹芯复合吸声覆盖层[7]等。圆柱空腔吸声覆盖层为共振吸声覆盖层的一种，通常由内部排列的周期性空腔粘弹性介质形成，空腔的基本形状为圆柱、圆台或喇叭形等截面且随厚度变化。对该结构的吸声覆盖层研究方法有：① 基于粘弹性介质中波传播特性的解析计算方法[3,8-9]，其区别在于所得波传播特性精确[3]或等效[8-9]；② 基于有限元的数值计算方法[1-2,10]。数值计算方法可计算相对复杂结构，但物理意义不明确；解析方法虽物理意义明确，便于分析其本质，但无法计算复杂的声学结构。

吸声覆盖层的机理分析及声学特性计算虽有较多研究成果，但对吸声覆盖层优化设计研究较少。吸声覆盖层设计涵盖材料、结构、工艺等多方面，主要技术为声学设计，即对吸声覆盖层基底材料及空腔结构设计、优化。吸声覆盖层优化设计即通过合适的优化算法合理设计吸声覆盖层结构尺寸与材料参数，使吸声覆盖层达到最优降低反射系数要求。但目前研究成果多集中于单个结构参数或单个材料参数[3,6,10]对吸声性能影响规律，而多参数同时变化进而改变吸声性能研究成果较缺乏。由于吸声覆盖层声学性能与材料属性、结构参数呈非线性复杂关系，不适用经典的搜索算法。随计算机性能提高及现代优化算法如遗传算法、模拟退火算法等发展，使建立合理有效的吸声覆盖层材料及结构参数综合优化方法成为可能。

本文对圆柱空腔吸声覆盖层的二维理论模型进行简化，以获得能快速准确计算吸声覆盖层声学性能的简化模型。并结合遗传算法，通过对吸声覆盖层基底介质材料参数及空腔结构的优化分析，建立圆柱空腔吸声覆盖层材料与结构参数的综合优化设计方法。

1 吸声覆盖层声学特性简化模型

圆柱空腔吸声覆盖层结构沿厚度方向形成空腔，其基本形状为圆柱型或圆台形，见图1(a)，按正三角形周期性排列相同空腔。因对称性只取其中一个单元分析。由于建立六面棱柱体理论模型较困难，故用圆柱代替简化模型的复杂性，见图1(b)。

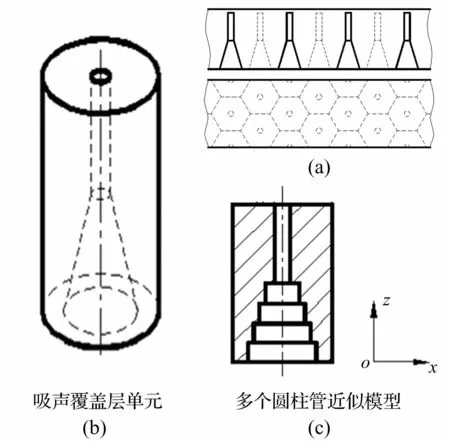
图1 典型圆柱空腔吸声覆盖层及单元结构示意图

汤渭霖等[3,11]建立的圆柱空腔吸声覆盖层二维理论将吸声覆盖层模型简化为截面连续变化的多个粘弹性圆柱管组合，其声学特性由波在圆柱管中传播、损耗特性决定。但该模型因考虑高阶轴对称波对声学特性的贡献，使计算分析过程复杂繁琐。因此，需基于二维理论寻找合理快速的近似方法，该方法主要基于两个近似：①平面波垂直入射时，吸声覆盖层低频性能由粘弹性圆柱管中最低阶轴对称波传播特性决定[11]，进而粘弹性圆柱管等效阻抗由最低阶轴对称波传播波数确定。②对圆柱-圆台空腔，近似为截面阶梯变化的多个圆柱管组合，见图1(c)，每段圆柱管有等效阻抗，整个圆柱管可视为多个阻抗变化的传输线组合。

平面波垂直入射时，吸声覆盖层中轴对称波传播特性可通过求解轴对称波的特征方程获得，即：

(1)

其中：

(2)

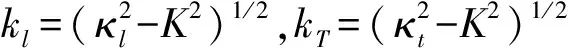
式(1)的详细建立过程见文献[3]。对给定的结构参数及材料属性，求解式(1)可得一组复根Km(m=1,2,…)，并由此确定kl,m，kt,m。此求解在复平面进行，K的实部为传播常数，虚部反映传播衰减。

二维理论给出吸声覆盖层单元-粘弹性圆柱管中位移、应力表达式[3]：

(3)

其中：RΦ,m为声波在吸声覆盖层后端面(z=0)即背衬反射系数;下标m表示第m阶轴对称波传播模式，j表示圆柱管截面第j圆环区域，m=j为能计算吸声覆盖层反射系数或吸声系数的必要条件。式(3)中ζmj(V)，ζmj(W)为关于吸声覆盖层结构、材料的复杂函数，即：

(4)

其中：αA,m,αB,m,αC,m为式(1)的代数余子式。参数V,W可表示为：

(5)

当仅考虑最低阶轴对称波(m=j=1)时，粘弹性圆柱管的等效阻抗可写为：

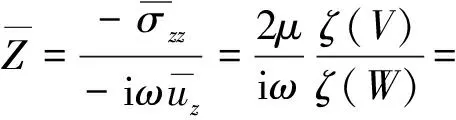
(6)

经推导、简化，式(6)可写成简单形式：

(7)

至此，粘弹性圆柱管前端面(z=H，上标f表示)、后端面(z=0，上标b表示)处位移及应力可通过传递矩阵T相联系，即：

(8)

总传递矩阵可写成每段圆柱管传递矩阵的连乘形式：

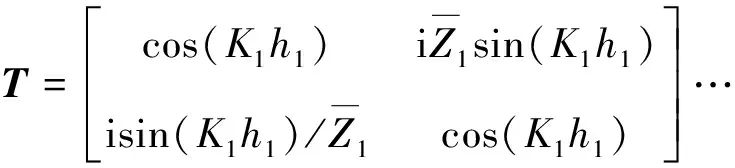
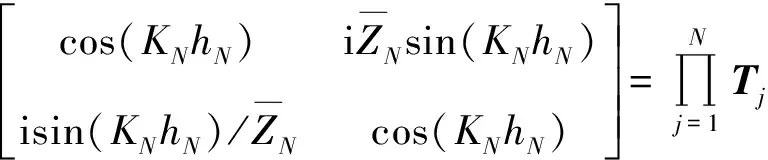
(9)

当粘弹性圆柱管后端面(背衬)的阻抗Zb已知时，前端面表面阻抗可由式(8)获得：

(10)

吸声覆盖层反射系数可写成：

(11)

式中：Zw为水介质特性阻抗。

2 基于遗传算法的吸声覆盖层参数优化

由以上推导看出，吸声覆盖层反射系数或吸声系数为关于基底介质材料属性及结构参数的复杂函数，单纯优化吸声覆盖层结构参数或材料属性，难在宽频范围内具备较高吸声系数，而二者同时优化则可能实现宽频吸声目标。吸声覆盖层结构参数包括穿孔率、空腔高度等；材料参数包括基底介质密度、泊松比、杨氏模量及损耗因子等。而杨氏模量及损耗因子大小与频率有关，较难用传统的搜索算法解决。因此本文用遗传算法进行吸声覆盖层多目标参数优化研究。

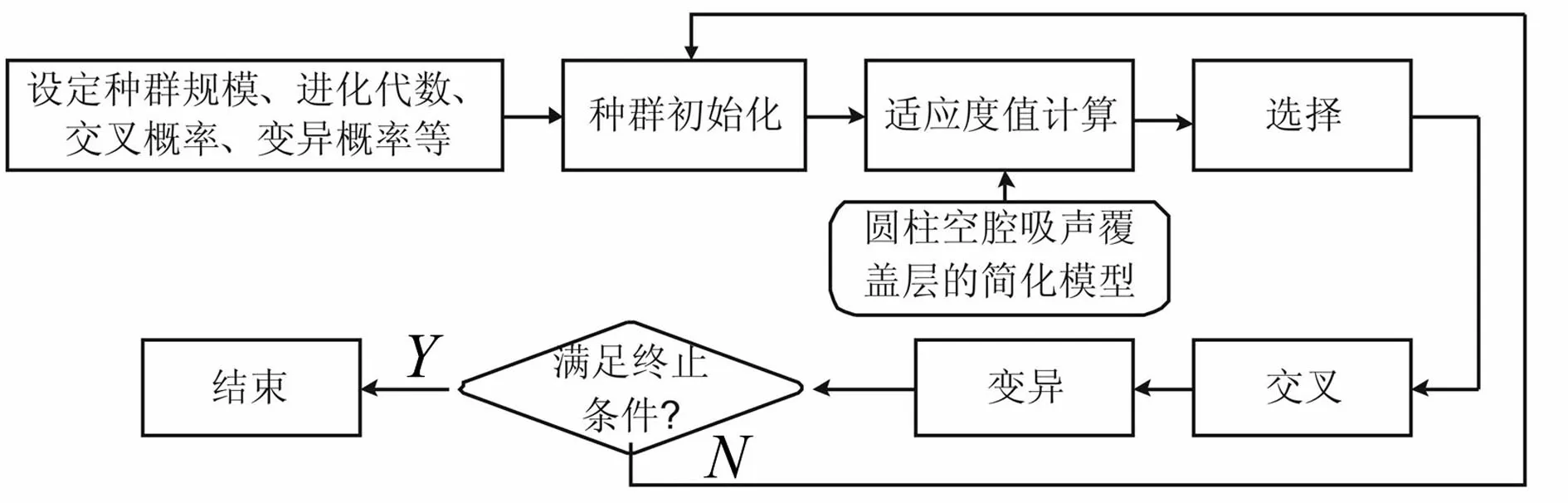
图2 遗传算法流程图

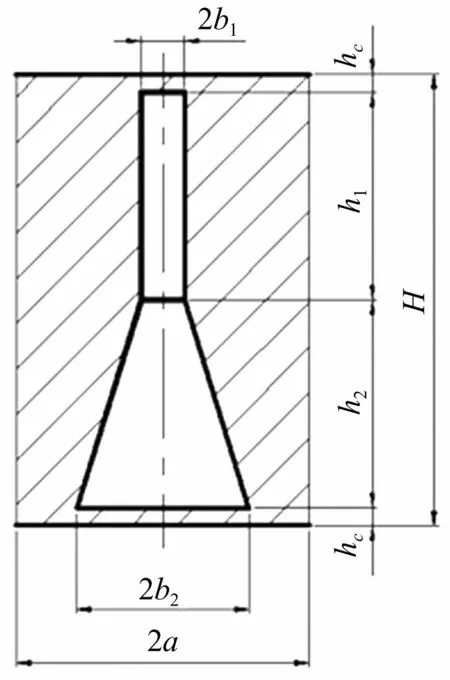
图3 圆柱-圆台空腔吸声覆盖层单元结构示意图

与传统优化方法相比，遗传算法、模拟退火算法等在解决大规模非线性优化问题时优势明显。其中遗传算法为借鉴生物界自然选择、自然遗传机制的随机搜索算法，较适用于处理传统搜索算法难以解决的复杂、非线性优化问题。遗传算法流程图见图2。遗传算法由随机产生的初始解开始搜索，通过选择、交叉、变异操作逐步迭代产生新解。该算法优点即将参数编码成染色体后进行优化，而不针对参数本身，因而不受函数约束条件限制；搜索过程由解的一个集合开始，而非单个个体，具有隐含并行搜索特性，可大大减少陷入局部最小的可能性，且计算时不依赖于梯度信息，不要求目标函数连续可导，较适合求解传统搜索算法难以解决的大规模、非线性组合优化问题。

用遗传算法对图3吸声覆盖层进行优化。该吸声覆盖层单元间按正三角形方式排列，据上述简化方式，每个单元可简化为半径a的圆柱体，且每个单元中包含圆柱、圆台两段空腔结构，圆柱空腔半径及圆台空腔上表面半径均为b1，圆台空腔下表面半径为b2，圆柱空腔及圆台空腔高度分别为h1，h2，空腔两端均有厚度为hc的封口薄层，整个吸声覆盖层高度为H=h1+h2+2hc。平面波由圆柱空腔一侧垂直入射到吸声覆盖层，吸声覆盖层背衬条件为绝对软背衬。

用遗传算法进行优化时，目标函数选择为：

(12)

据遗传算法理论，在MATLAB软件中编写实现基本遗传算法程序以寻找目标函数最优解。遗传算法参数设置：种群规模100，进化次数100，交叉概率0.8，变异概率0.2。

2.1 算例1(材料属性优化)

只优化吸声覆盖层基底介质的粘弹性动态力学参数，即材料杨氏模量及损耗因子。由于粘弹性材料的动态力学参数非常数，随频率变化呈色散关系，故假设粘弹性材料的杨氏模量及损耗因子随频率成二次函数关系[6]，即：

(13)

式中：f为频率；E为杨氏模量(Pa)。若只考虑吸声覆盖层由一种基底介质构成，需优化6个参数p0～p2，q0～q2。由此可计算不同频率处的杨氏模量及损耗因子，进而用简化模型计算反射系数。

经优化的6个参数及设定的覆盖层单元各结构参数见表1。“*”表示未优化参数(下同)，在该算例中为单元各结构参数。吸声覆盖层厚度H=50 mm。

表1 吸声覆盖层优化后材料属性及未优化结构参数

吸声覆盖层基底介质的杨氏模量及损耗因子经优化的吸声系数见图4，经优化的杨氏模量及损耗因子见图5。由图4看出，吸声覆盖层最低吸声频率约2 kHz，在2～8 kHz频率范围内，平均吸声系数约0.86。

图4 吸声覆盖层材料参数优化后吸声系数

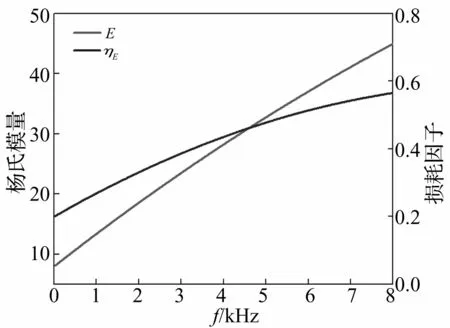
图5 优化后杨氏模量及损耗因子

2.2 算例2(材料属性、结构参数综合优化)

在算例1基础上进行材料属性、结构参数综合优化。待优化结构参数包括圆柱空腔半径b1、圆台下表面空腔半径b2、圆柱空腔高度h1，圆台空腔高度可据h2=H-h1-2hc计算获得，而吸声覆盖层厚度H与封口薄层厚度hc设定不变。因此，待优化参数包括与基底材料杨氏模量与损耗因子有关的6个系数、3个结构参数计9个参数。

表2 吸声覆盖层优化后材料属性与结构参数

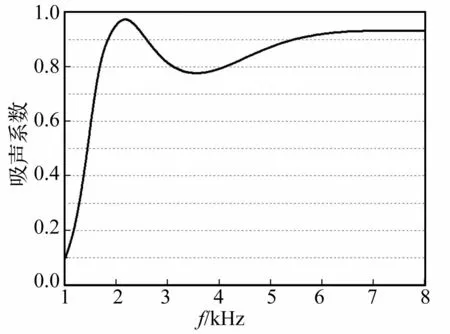
图6 吸声覆盖层材料及结构参数优化后吸声系数

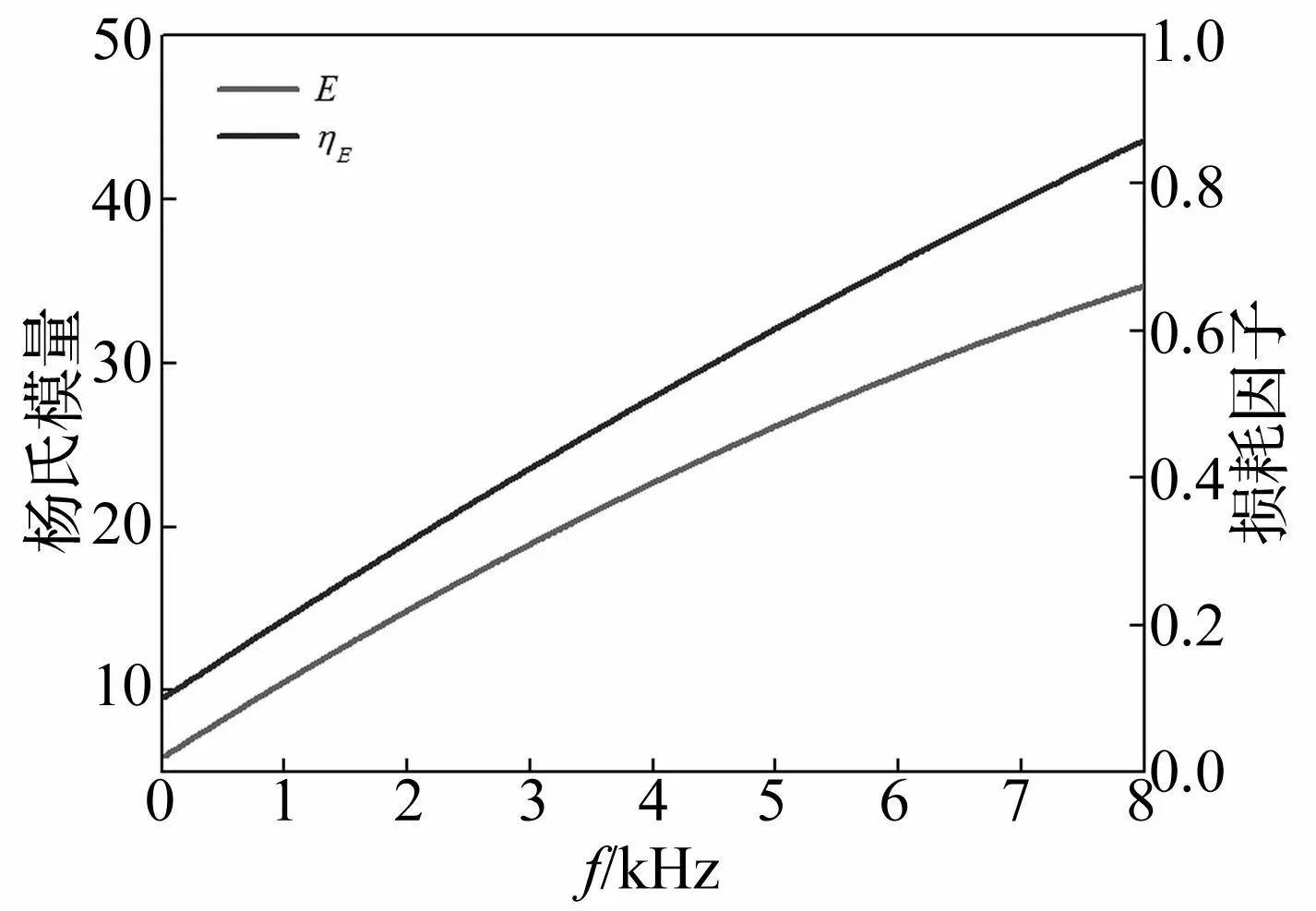
图7 优化后杨氏模量及损耗因子

经优化后9个参数及设定的其它结构参数见表2，吸声覆盖层材料及结构参数经综合优化后吸声系数见图6，经综合优化后基底介质杨氏模量及损耗因子见图7。由图6看出，吸声覆盖层最低吸声频率仍为2 kHz左右，而在 2～8 kHz频率范围内，平均吸声系数约0.89。与算例1比较知，若同时优化吸声覆盖层材料及结构参数，可获得吸声性能更好的材料属性与结构参数组合。

2.3 算例3(两层材料属性及结构参数综合优化)

考虑更复杂情况，设吸声覆盖层由两种基底介质构成：包含圆柱空腔部分为第一种介质，包含圆台空腔部分为第二种介质，即两种介质以圆柱空腔及圆台空腔的交界处为边界。需优化的参数包括与第一种材料杨氏模量及损耗因子相关的6个系数(以上标“(1)”表示)、与第二种材料杨氏模量及损耗因子相关的6个系数(以上标“(2)”表示)、3个结构参数计15个待优化参数。

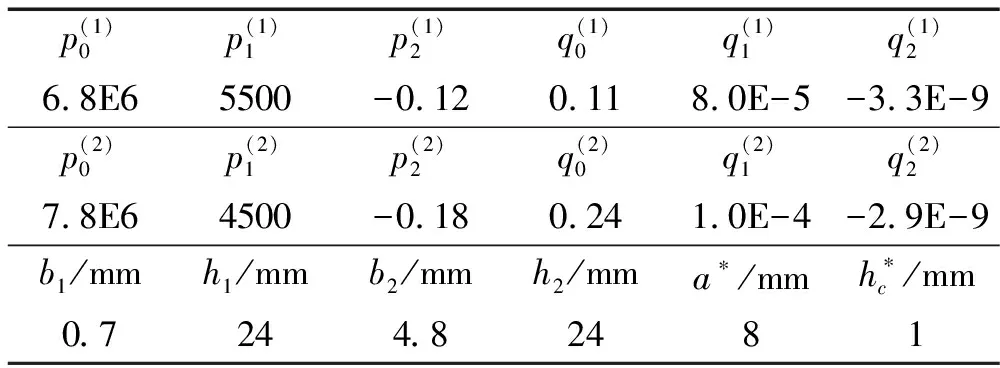
表3 吸声覆盖层优化后两层材料属性及优化后结构参数

优化后15个参数、设定的其它结构参数见表3，吸声覆盖层,两层材料属性及结构参数经综合优化后吸声系数见图8，优化后第一层介质杨氏模量及损耗因子见图9，优化后第二层材料杨氏模量及损耗因子见图10。由图8看出，吸声覆盖层最低吸声频率略高于2 kHz, 在2～8 kHz频率范围内，平均吸声系数约0.93。与前两种优化模型相比，平均吸声系数明显提高，原因为考虑吸声覆盖层分层后，吸声覆盖层实现阻抗渐变形式，使波在多层结构中传播时遭遇阻抗变化并发生多次反射、透射，模式转换可产生更多的能量损耗，从而提高宽频吸声能力。而阻抗渐变形式不仅可通过结构分层实现，也可通过材料分层实现。

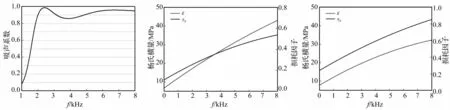
图8 吸声覆盖层材料及结构参数优化后吸声系数

3 结 论

(1) 圆柱空腔吸声覆盖层材料属性与结构参数存在一组使吸声覆盖层在工作频段内具有高吸声系数的最佳值，该值可由参数优化方法获得。

(2) 较多需优化参数尤其粘弹性材料动态力学参数(杨氏模量、损耗因子)为频率函数，常规搜索算法无法解决此类大规模非线性优化问题。

(3) 本文建立的圆柱空腔吸声覆盖层性能分析简化模型，通过用遗传算法进行吸声覆盖层材料属性及结构参数优化分析，仿真算例表明，综合优化材料属性及结构参数可获得更佳的宽频吸声性能。

(4) 本文所建优化模型可进行更多参数优化分析，亦为吸声覆盖层优化设计提供可行计算方法。

参 考 文 献

[1]Hennion A C, Decarpigny J N. Analysis of the scattering of a plane acoustic wave by a doubly periodic structure using the finite element method: application to alberich anechoic coatings [J]. Journal of the Acoustical Society of America, 1991, 90(6):3356-3367.

[2]Easwaran V, Munjal M L. Analysis of reflection characteristics of a normal incidence plane wave on resonant sound absorbers: a finite element approach [J]. Journal of the Acoustical Society of America, 1993, 93(3):1308-1318.

[3]汤渭霖, 何世平, 范 军. 含圆柱形空腔吸声覆盖层的二维理论[J]. 声学学报, 2005, 30(4):289-295.

TANG Wei-lin, HE Shi-ping, FAN Jun. Two-dimensional model for acoustic absorption of viscoelastic coating containing cylindrical holes [J]. Acta Acustica, 2005, 30(4): 289-295.

[4]Zhao H G, Liu Y Z, Wen J H, et al. Tri-component phononic crystals for underwater anechoic coatings[J]. Physics Letters A, 2007, 367(3): 224-232.

[5]Ivansson S M. Numerical design of alberich anechoic coatings with superellipsoidal cavities of mixed sizes[J]. Journal of the Acoustical Society of America, 2008, 124(4): 1974-1984.

[6]王仁乾, 马黎黎. 吸声材料的物理参数对消声瓦吸声性能的影响[J]. 哈尔滨工程大学学报, 2004, 25(3): 288-294.

WANG Ren-qian, MA Li-li. Effects of physical parameters of the absorption material on absorption capability of anechoic tiles[J]. Journal of Harbin Engineering University, 2004, 25(3): 288-294.

[7]朱 锡, 罗 忠, 周 欣,等. 斜入射下水中隐身夹芯复合材料壳板结构声学设计[J]. 船舶力学, 2009, 13(4): 646-656.

ZHU Xi, LUO Zhong, ZHOU Xin, et al. Acoustic stealth design on the underwater sandwich composite shell structure in oblique incidence [J]. Journal of Ship Mechanics, 2009, 13(4): 646-656.

[8]何祚镛, 王 曼. 水下非均匀复合层结构吸声的理论研究[J]. 应用声学, 1996, 15(5):12-19.

HE Zuo-yong, WANG Man. Investigation of the sound absorption of non-homogeneous composite multiple-layer structures in water [J]. Applied Acoustics, 1996, 15(5): 12-19.

[9]朱蓓丽, 任克明. 等效参数法研究带圆柱通道橡胶体的声学性能[J]. 上海交通大学学报, 1997, 31(7): 20-24.

ZHU Bei-li, REN Ke-ming. Acoustic properties analysis of elastomer with cylindrical bores using equivalent parametric method [J]. Journal of Shanghai Jiaotong University, 1997, 31(7): 20-24.

[10]Panigrahi S N, Jog C S, Munjal M L. Multi-focus design of underwater noise control linings based on finite element analysis[J]. Applied Acoustics, 2008, 69(12): 1141-1153.

[11]何世平, 汤渭霖, 何 琳,等. 变截面圆柱形空腔覆盖层吸声系数的二维近似解[J]. 船舶力学, 2006, 10(1): 120-127.

HE Shi-ping, TANG Wei-lin, HE Lin, et al. Analysis of acoustic characteristics of anechoic coating containing varying sectional cylindrical cavity [J]. Journal of Ship Mechanics, 2006, 10(1): 120-127.