计电磁不平衡拉力的高速电主轴转子偏心特性研究

陈小安， 张 朋， 陆永亚， 合 烨， 刘俊峰

(重庆大学 机械传动国家重点实验室，重庆 400044)

高速旋转机械的高速电主轴转子系统偏心状态会引起主轴剧烈振动，不但影响数控机床加工精度，且会导致电主轴失效[1-2]。将转子偏心引起的离心力载荷作为高速电主轴主要外载荷研究较多。Hongqi等[3-4]通过建立的高速电主轴热-机耦合动力学模型，在对动力特性研究中发现，离心力载荷是转子系统的重要外载荷。Jorgensen等[5-6]据影响系数法建立高速电主轴动力学模型，讨论不同工况离心力载荷对转子动力学行为响应。Nelson[7]用Timoshenko梁理论建立高速电主轴动力学模型，并详细分析离心力载荷计算方法。

本文将高速电主轴转子偏心状态引起的另一重要载荷-电磁不平衡拉力考虑入转子外载荷，分析两种外载荷对转子动态特性影响；计算轴承动态支撑刚度随转速的变化及对转子系统一阶固有模态影响；通过实验进行理论分析验证。

1 转子偏心载荷模型

制造、装配等误差易导致高速电主轴转子系统偏心。高转速下转子系统偏心状态会产生附加载荷-电磁不平衡拉力载荷与离心力载荷。

1.1 电磁不平衡拉力载荷

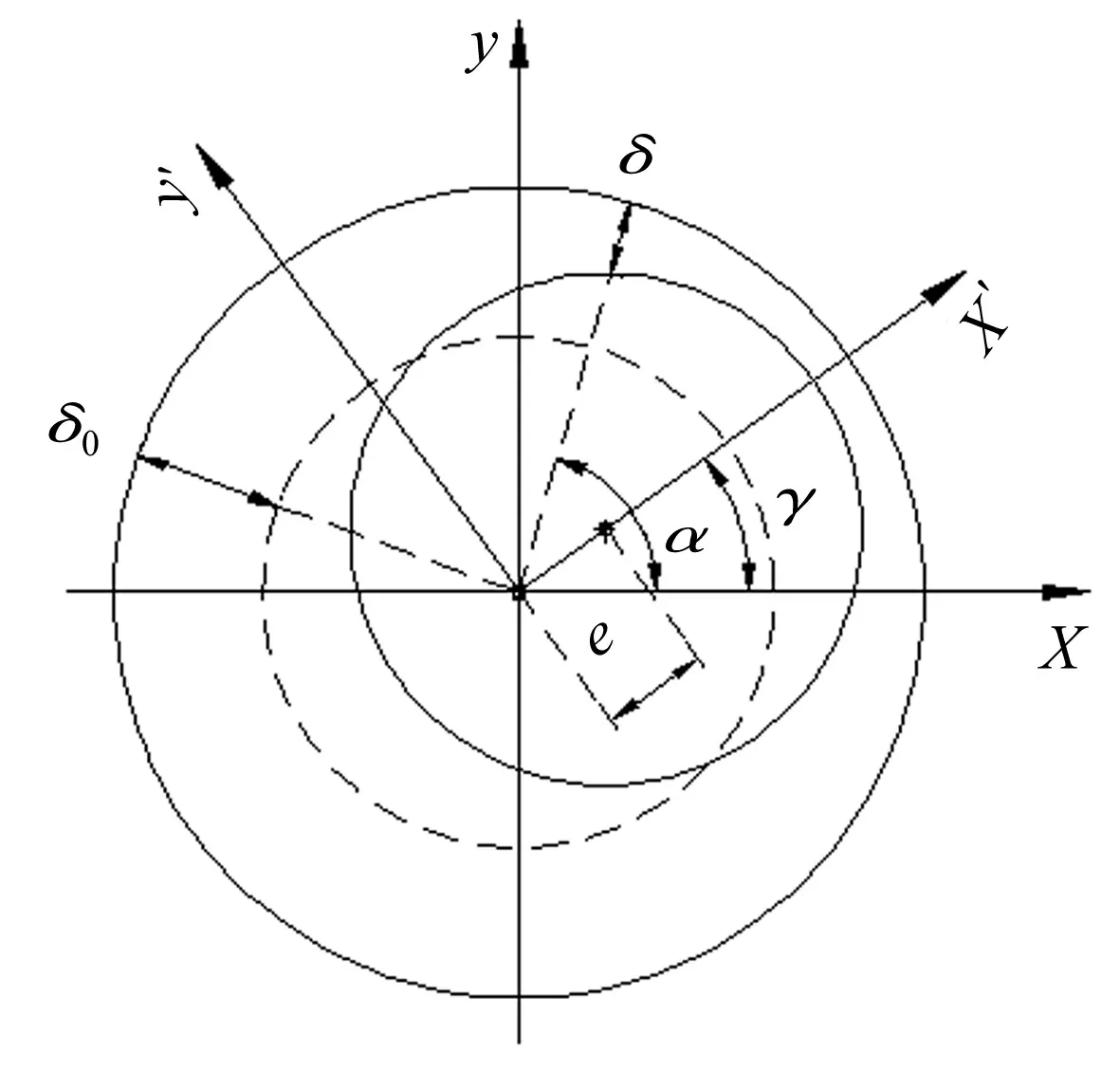
图1 转子偏心气隙

高速电主轴转子偏心时，电机定转子不对心会造成气隙磁场不均匀，导致转子系统径向附加磁拉力[8-9]。转子偏心见图1。图1中δ为实际气隙厚度；δ0为理想气隙厚度；e为定转子偏心距；α，γ分别为相互位置角。

实际气隙厚度为：

δ=δ0-ecos(α-γ)

(1)

气隙磁导为：

Λ=μ0/Kμδ

(2)

式中：μ0为空气导磁系数；Kμ=(K1δ0+δFe)/K1δ0为气隙饱和度，K1为平均气隙系数，δFe为铁磁材料当量气隙。

气隙合成磁动势为：

F=FScos(ωSt-α)+FRcos(ωSt-α-φ)

(3)

式中：FS，FR为定子、转子合成磁动势幅值；ωS为电机同步角频率；φ为转子电流相对于定子电流滞后角。

气隙磁密为：

B=ΛF

(4)

气隙磁密切向分量远小于径向分量，可忽略不计，则转子表面的麦克斯韦应力为：

σ=B2/2μ0

(5)

对转子表面的麦克斯韦应力进行周向积分，可得转子电磁不平衡磁拉力载荷幅值：

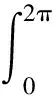
(6)

式中：R，L为电机转子半径、气隙长度。电磁不平衡拉力角频率与电机极对数无关，均为二倍转频[8]。

1.2 离心力载荷

转子偏心质量造成的离心力载荷幅值与转子转速平方成正比[3-4]，其幅值为：

FC=mω2e

(7)

式中：m为转子节点质量；ω为转子转频。由于离心力载荷由转子转动引起，故其角频率为一倍转频。

2 转子动力学模型

高速电主轴为典型的轴承-转子系统，考虑剪应变影响，用Timoshenko梁单元[10]耦合入轴承动态支承刚度[11]，对转子系统进行动力学建模。

2.1 轴承动态支承刚度矩阵

高速运行的角接触球轴承在轴向载荷Fa、径向载荷Fr及弯矩载荷M的联合作用下，内外圈会发生相对轴向位移δa、径向位移δr及角位移θ，轴承内部几何关系见图2：E，E’，m，m’分别为轴承运行前后钢球球心及内沟曲率中心；n为外沟曲率中心；α为钢球原始接触角；αij，αej分别为钢球与内外圈实际接触角；Rij为钢球与内圈接触半径；Axj，Azj为任意钢球位置Ψj处内沟曲率中心坐标；Vxj，Vzj为钢球球心位置参数。

图2 轴承内部几何关系

据套圈控制理论及赫兹接触理论[12]，联立钢球平衡方程与内圈平衡方程得轴承拟静力平衡方程为：

Fb=Kbδb

(8)

式中：Fb为内圈载荷列向量；Kb为动态支承刚度矩阵；δb为轴承内圈位移列向量。

2.2 转子动力学方程

耦合入轴承动态支承刚度矩阵，以电磁不平衡拉力与离心力为外载荷的高速电主轴转子动力学方程为：

Ms{X″}+Cs{X′}+(Ks+Kb){X}={FM}+{FC}

(9)

式中：Ms，Cs，Ks分别为转子质量矩阵、阻尼矩阵、刚度矩阵；{X″}，{X′}，{X}为节点加速度、速度、位移向量；{FM}，{FC}分别为电磁不平衡拉力载荷向量、离心力载荷向量。

3 仿真、实验结果及分析

3.1 轴承动态支承刚度

本文以2GDZ15型高速电主轴为分析对象，其轴承型号为B7011CD/P4A，B7009CD/P4A。定位预紧，据生产厂的参数计算轴承动态支承刚度。由于轴承径向刚度对转子一阶固有频率影响较大，本文给出前后轴承四种转速的径向支承刚度，见图3。由图3看出，随转速的升高，定位预紧时角接触球轴承径向支承刚度随之增大，且增幅较大。

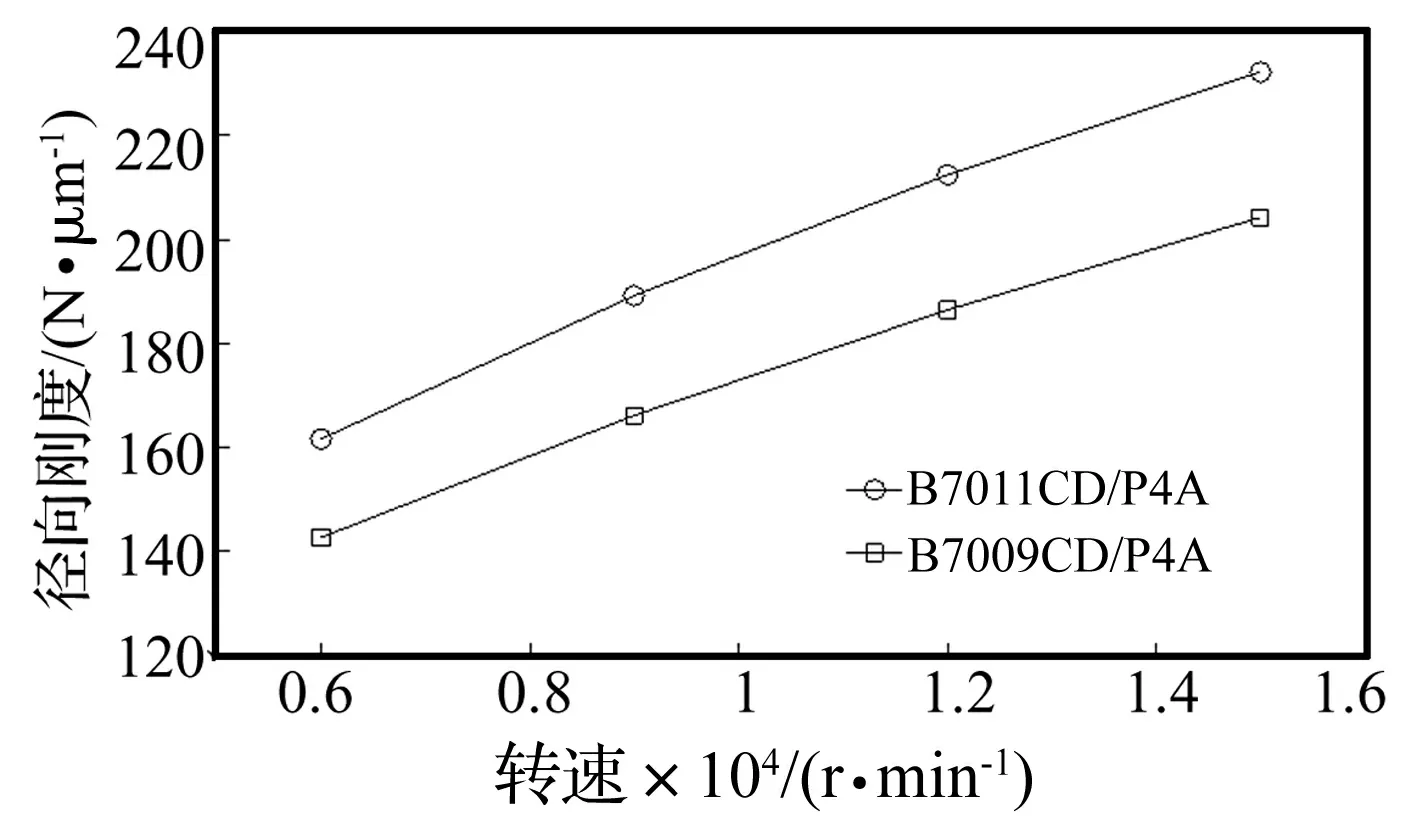
图3 轴承径向支承刚度

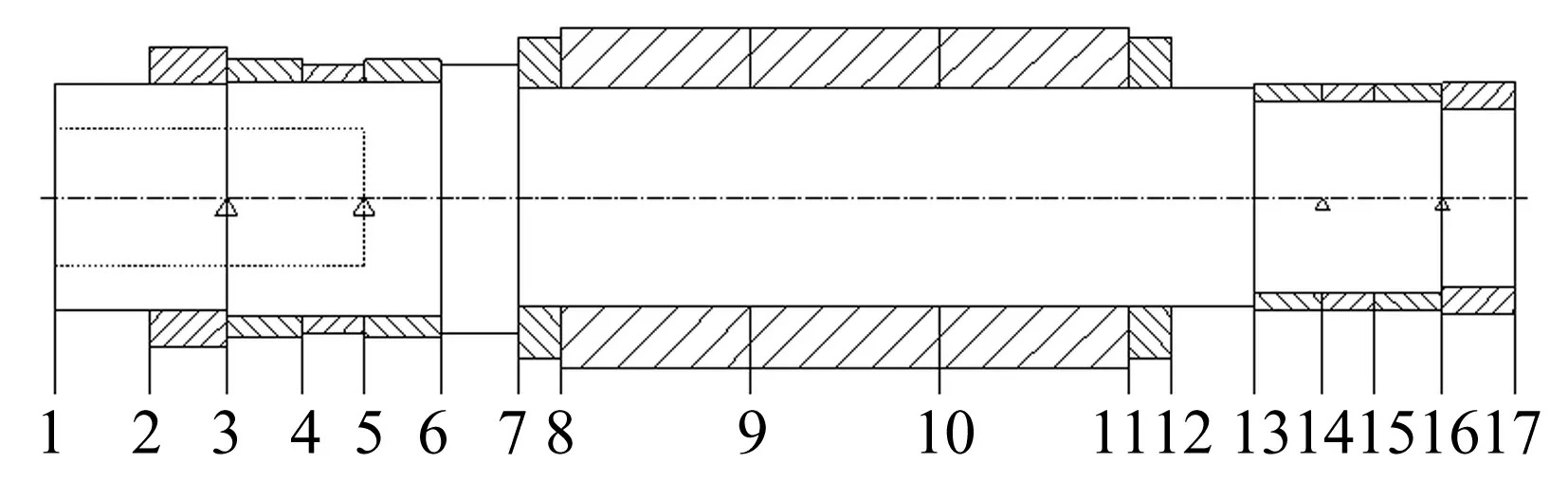
图4 转子有限元模型

3.2 转子动力学建模

2GDZ15型高速电主轴转子系统有限元模型见图4。转子整体分为16个单元，17个节点；芯轴上附加转动零件简化成圆环；轴承支撑位于三角形处。

3.3 转子模态仿真

据有限元法基本理论构建转子动力学方程，用子空间迭代法求解一阶模态。不同转速的一阶固有频率见表1。

表1 转子一阶固有频率

转子一阶固有振型为径向振动，最大振幅出现在转子尾部，其一阶阵型见图5。

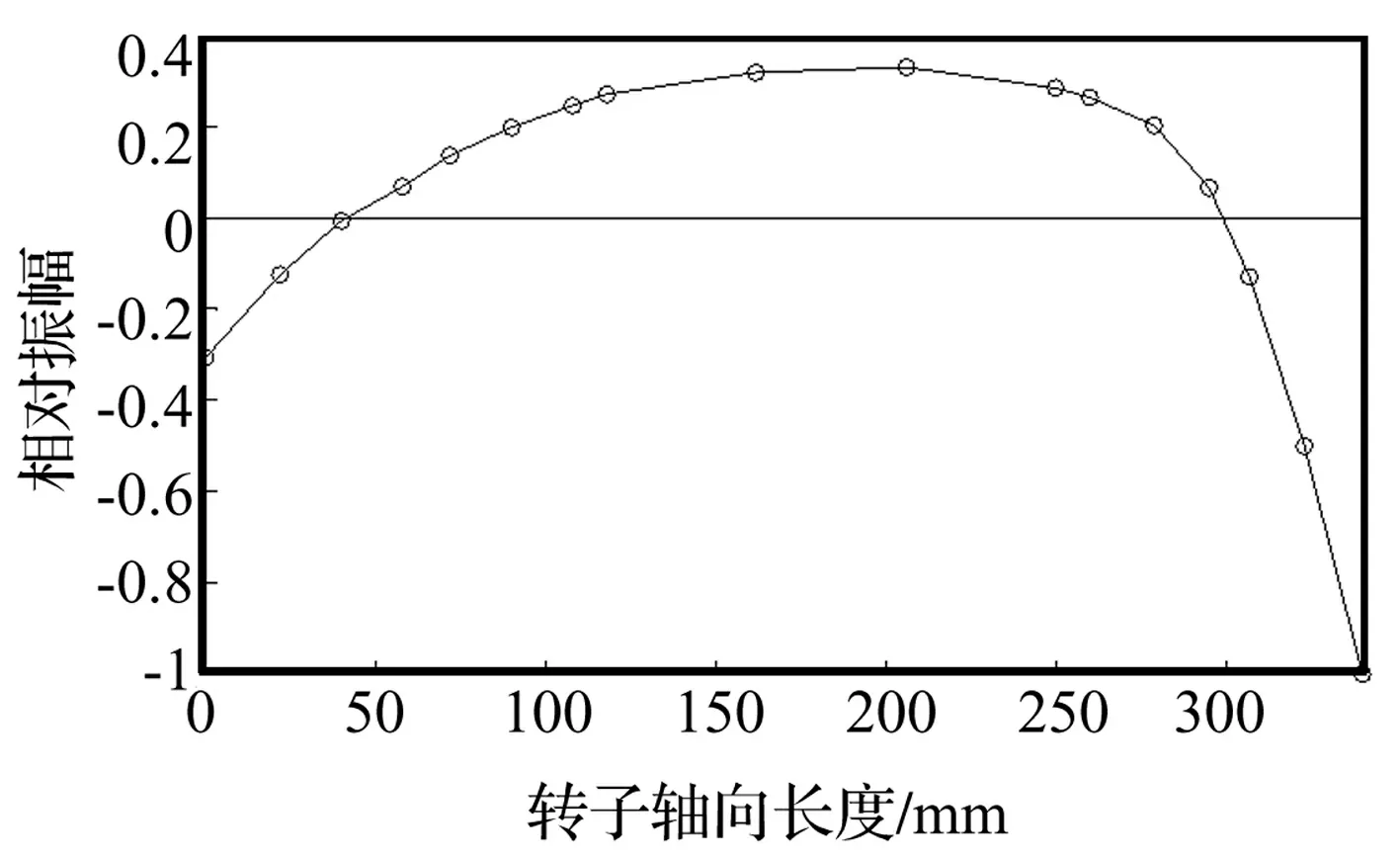
图5 转子一阶固有振型

3.4 转子振动实验

实验装置包括2ZDG15型高速电主轴、WD501型电涡流式位移传感器及前置器、B&K2692-014电荷放大器、SC305-UTP型数据采集分析仪及信号处理分析软件。电主轴运行稳定后，用电涡流位移传感器测量电主轴转子前端径向振动位移，采样频率4 096 Hz，采样时间1 s。测试分析流程见图6。

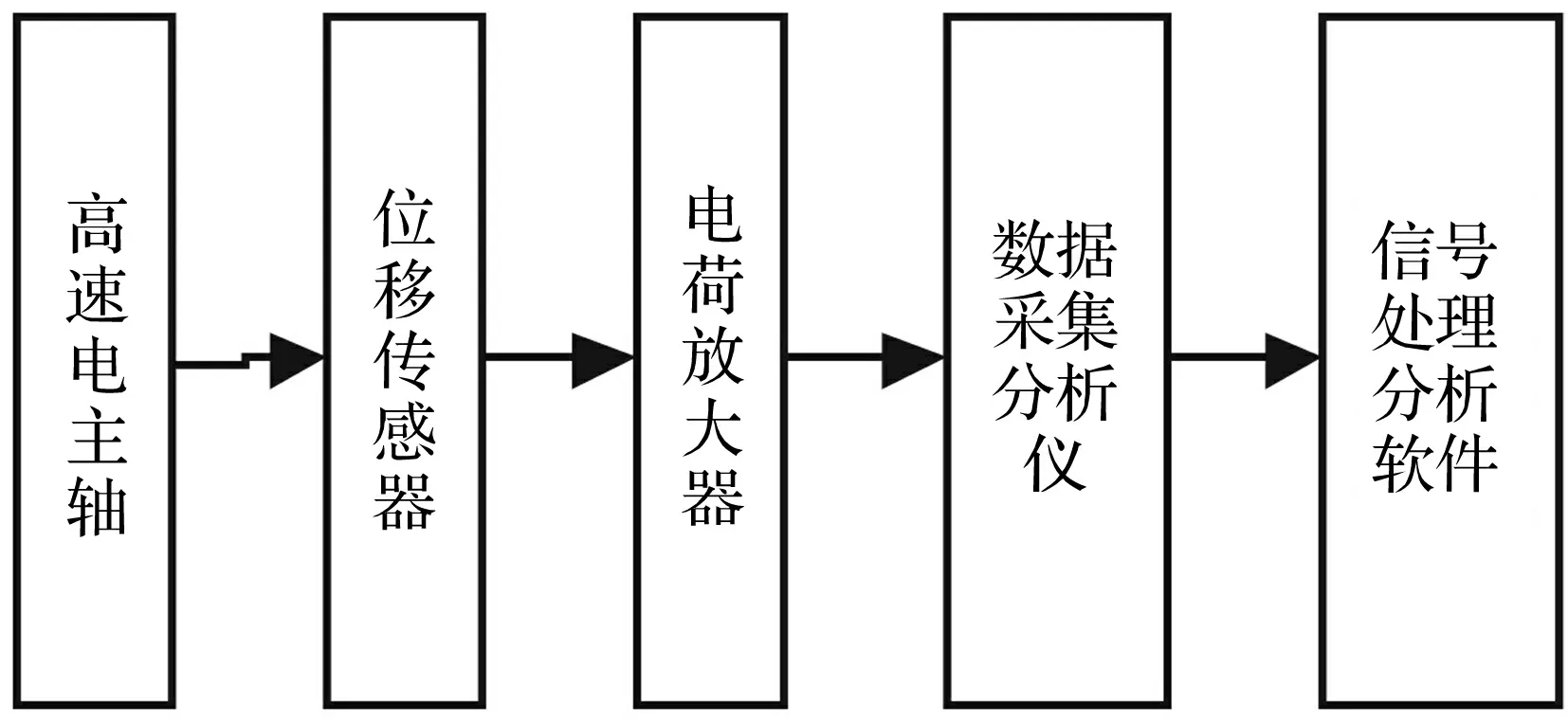
图6 振动测试分析流程图

3.5 试验结果及分析

对位移振动信号进行频谱分析，不同转速的电主轴前端径向位移振动信号频谱见图7。

图7 振动信号频谱图

不同转速时一、二倍转频处均出现振动峰值，分别对应转子偏心引起的离心力载荷及电磁不平衡拉力载荷，说明两种偏心载荷确为引起电主轴振动的重要激振力。随转速的升高，一、二倍转频处振动幅值随之升高，导致偏心载荷增大，对应频率处的振动幅值亦增大。由于噪声信号影响，电主轴转子一阶固有频率处产生的共振振幅值较大。但随转速的升高，一阶固有频率随之升高，因为轴承径向动态支承刚度随转速的增大而增大，导致转子系统固有频率随转速的升高而升高。计算结果与实验相比，四种转速时误差分别为5.76%，5.33%，4.43%，3.88%。

4 结 论

(1) 高速电主轴转子偏心会引起电磁不平衡拉力载荷与离心力载荷，随转速的升高，振动幅值增大，转子偏心加剧，两种载荷随之增大。对转子动态特性影响较大，振动频谱对应频率处均出现较大峰值。

(2) 由于噪声信号影响，转子一阶固有频率处产生共振，频谱出现峰值；随转速的升高，轴承径向动态支撑刚度增大，导致转子系统一阶固有频率升高。

(3) 据2ZDG15型高速电主轴转子偏心时载荷理论分析及振动实验验证，偏心载荷是电主轴振动的主要来源。高品质电主轴制造须进行严格动平衡，或设计在线动平衡调节装置[13]，以保证电主轴转子振动幅值在允许范围内。

参 考 文 献

[1]Abele E, Altintas Y, Brecher C. Machine tool spindle units [J]. CIRP Annals-Manufacturing Technology, 2010, 59(2):1-22.

[2]Jedrzejewski J, Kowal Z. High-speed precise machine tools spindle units improving[J]. Journal of Materials Processing Technology, 2005, 162-163: 615-621.

[3]Li H Q,Shin Y C.Integrated dynamic thermo-mechanical modeling of high speed spindles, part 1: model development [J]. Journal of Manufacturing Science and Engineering, Transactions of the ASME, 2004, 126(1):148-158.

[4]Li H Q,Shin Y C.Integrated dynamic thermo-mechanical modeling of high speed spindles, part 2: solution procedure and validations[J]. Journal of Manufacturing Science and Engineering, Transactions of the ASME,2004,126(1):159-168.

[5]Jorgensen B R, Shin Y C. Dynamics of machine tool spindle/bearing systems under thermal growth[J]. Journal of Tribology, ASME, 1997, 119(4): 875-882.

[6]Jorgensen B R, Shin Y C. Dynamics of machine tool spindle/bearing systems under thermal growth [J]. Journal of Manufacturing Science and Engineering, ASME, 1998, 120(4): 387-394.

[7]Nelson H D. A finite rotating shaft element using timoshenko beam theory[J]. Journal of Mechanical Design, ASME, 1980, 102(4):793-803.

[8]Guo D, Chu F, Chen D. The unbalanced magnetic pull and its effects on vibration in a three-phase generator with eccentric rotor[J]. Journal of Sound and Vibration,2002,254(2): 297-312.

[9]Im H, Yoo H H, Chung J. Dynamic analysis of a bldc motor with mechanical and electromagnetic interaction due to air gap variation[J]. Journal of Sound and Vibration,2011,330(8): 1680-1619.

[10]Han S M, Benaroya H, Wei T. Dynamics of transversely vibrating beams using four engineering theories[J]. Journal of Sound and Vibration, 1999, 225(5): 935-988.

[11]李松生, 陈晓阳, 张 钢,等. 超高速时电主轴轴承的动态支承刚度分析[J].机械工程学报, 2006, 42(11): 60-65.

LI Song-sheng, CHEN Xiao-yang ZHANG Gang,et al. Analysis of dynamic supporting stiffness about spindle bearings at extra high-speed in electric spindles[J]. Chinese Journal of Mechanical Engineering, 2006, 42(11): 60-65.

[12]Jones A B. A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions [J]. Journal of Basic Engineering, AMSE, 1960, 82(2):309-320.

[13]樊红卫, 景敏卿, 刘 恒. 主动混合式砂轮-电主轴系统自动平衡装置研究综述[J]. 振动与冲击, 2012, 31(5): 26-31.

FAN Hong-wei, JING Min-qing, LIU Heng. Review for studying on active hybrid auto-balancer of grinding wheel and motor spindle[J]. Journal of Vibration and Shock, 2012, 31(5): 26-31.