基于相对适应度遗传算法的高层结构粘滞阻尼器优化布置

燕乐纬, 陈洋洋， 王 龙， 苏 成

(1.广州大学 土木工程学院，广州 510006; 2. 广州市建筑集团有限公司，广州 510030;3. 广州大学 工程抗震研究中心，广州 510006; 4. 华南理工大学 土木与交通工程学院，广州 510641)

粘滞阻尼器作为被动减震控制装置[1]广泛应用于高层、超高层建筑结构。早期消能减震体系研究中，粘滞阻尼器被均匀分布于高层建筑各层。随结构层数及阻尼器数量的增加，优化阻尼器布置、降低消能减震系统成本、提高耗能效率成为布置消能装置须考虑的问题之一[2-3]。在建筑结构阻尼器优化布置研究中，大多采用遗传算法[4]。对给定阻尼器可选安装位置，有安装阻尼器与不安装阻尼器两种状态并用{1,0}表示，恰对应遗传算法的一基因位。将所有可选安装位置状态列入一数列中，即形成标准遗传算法染色体[5]。对该染色体进行遗传优化，所得最佳染色体即为优化问题最优解、阻尼器最优布置方案[6]。

由于遗传算法求解过程无需目标函数梯度信息且具有本质并行性特点，用遗传算法能有效实现阻尼器安装位置优化。但标准遗传算法本身存在计算效率低、易于早熟收敛等问题[7]。若建筑物较高，需安装的阻尼器数量则较多，用遗传算法求解阻尼器优化布置会遇困难[8]。而阻尼器优化布置需综合考虑结构安全性、舒适度要求，设定适当目标函数，使优化结果满足不同工程需求，为目前研究热点。

利用遗传算法处理工程中优化问题[9-10]，本文在此基础上，对遗传算法针对性改进，用于求解建筑物较高、阻尼器数量较多、优化设计空间容量较大、难用一般优化方法或穷举法求解的高层建筑阻尼器优化布置问题。并对优化目标函数构造进行探讨，提出考虑多种地震波作用的改进目标函数。

1 计算模型

1.1 结构模型

通常线性粘滞阻尼器出力取决于其瞬时相对速度大小[11]，即：

(1)

地震作用下，安装粘滞阻尼器的结构体系运动微分方程可表示为：

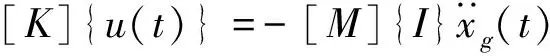
(2)

1.2 优化模型

理论上绝大多数阻尼器优化布置问题均可用遗传算法进行优化。但对层数过低或阻尼器数量少的结构，用遗传算法优化会有错失全局最优解概率，较穷举法无明显优势。建筑物较高、阻尼器数量较多、设计空间较大、难用穷举法或其它优化方法迅速求解的优化问题，遗传算法能充分发挥并行及鲁棒性好等优点，依概率收敛到优化问题的全局最优解。一般数学表达式为：

(3)

式中：n为结构层数；X为阻尼器布置方案；f为优化问题目标函数，据具体需求可采用最大层间位移角、顶层最大加速度、各层最大位移或各计算结果组合；t为动载荷作用时间；g(X,t)≤0为经标准化处理的约束条件。

1.3 目标函数

综合考虑最大层间位移角、顶层最大加速度及各层最大位移的无量纲目标函数[6]为：

(4)

式中：θ，α,u分别为结构在地震作用下层间位移角、绝对加速度、绝对位移；下标max表示有控结构响应最大值，0，max表示无控结构响应最大值。α,β,γ为加权系数。本文据优化问题特点，对加权系数选取作初步探讨并改进。

2 相对适应度遗传算法

2.1 轮盘赌选择与界限构造法模型

标准遗传算法采用轮盘赌选择算子。按轮盘赌，适应度为fi的染色体被选中概率为：

(5)

与锦标赛选择不同，用轮盘赌选择时，染色体适应度值有绝对意义，即适应度数值大小会直接影响被选中概率[12-13]。适应度函数有非负性要求，总希望越大越好。而结构振动控制问题目标却要求结构响应越小越好。为实现从目标函数值到适应度函数值的映射，用界限构造法构造适应度函数[14]，即：

F(x)=Cmax-f(x)

(6)

用此方法构造适应度函数关键在于预估目标函数值上限Cmax[15]。不仅适应度有非负的要求，且结构响应取值范围较难估算，只能选取几种典型的布置方案试算。为保证适应度F(x)非负，常给Cmax设定较大裕度，其结果不但改变目标函数值大小，且轮盘赌选择优胜劣汰选择意义被弱化，从而阻滞遗传算法进化过程，降低计算效率。

2.2 相对适应度函数

为解决以上问题，本文提出基于目标函数值相对大小的适应度函数构造方法。设规模为N的种群中，第i个染色体目标函数值为f(xi)，则适应度计算式为：

(7)

式中：max{f(x)}， min{f(x)}为当前种群中目标函数最大值、最小值。

按式(7)，若种群中所有染色体目标函数值完全相同(最大值等于最小值)，则所有染色体适应度值取相同正常数c；若各染色体目标函数值不同，则用max{f(x)}代替式(6)中Cmax。所得适应度称为相对适应度，基于相对适应度的轮盘赌选择算子称相对适应度选择算子，采用相对适应度选择算子的遗传算法称相对适应度遗传算法(Relative Fitness Genetic Algorithm，RFGA)。相对适应度函数意义在于：

(1) 界限值max{f(x)}为当前种群中目标函数最大值，会随种群进化不断变化，为一动态量。所选界限值不用预估Cmax即可保证F(x)非负性。

(2) 据式(7)计算所得相对适应度能直接体现种群中各染色体目标函数值间差异，使目标函数值(结构响应)小的染色体获得较大选择概率，目标函数值较大染色体获得较小选择概率。代表减震效果最差的阻尼器配置方案的目标函数值最大染色体直接被剔除。

如某规模为100的种群，一次迭代计算所得目标函数最小值为2.3×10-3，最大值为2.7×10-3，平均值为2.5×10-3。采用界限构造法(预设界限值Cmax=4×10-3)及相对适应度方法构造适应度函数时，不同层次染色体的选择概率见表1。由表1看出，采用相对适应度方法构造适应度函数时，最优染色体与最差染色体被选中概率差距明显大于界限构造法。优良染色体存活率大幅提高，有优良基因模式的能以最合理概率存活，而不良模式则以较大概率被摒弃。

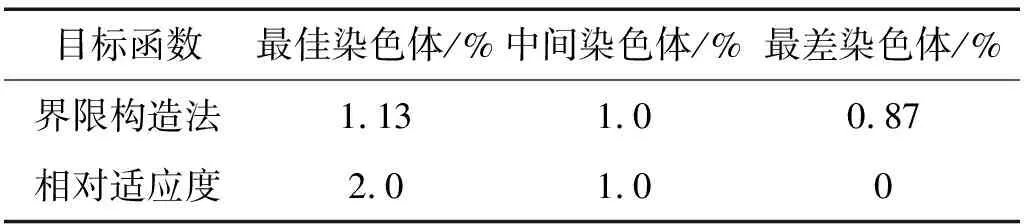
表1 采用不同适应度构造方法时选择概率

需指出的是，由于计算相对适应度所用界限值max{f(x)}为动态，相对适应度只对当前种群有意义。不同代种群的适应度计算标准不同，相互之间不可比较，不会出现标准遗传算法中种群适应度平均值及最优值随繁殖代数升高的适应度曲线。采用相对适应度时，为观测种群进化过程，可用目标函数值进化曲线代替。随种群的进化及优良模式的不断产生，种群目标函数平均值及最优值会随繁殖代数的增加逐渐减小，收敛于最优解。

2.3 算例验证

用工程算例验证基于RFGA高层结构阻尼器优化布置方法的适用性及计算效率，并与带精英保持策略的标准遗传算法(SGA)对比。某20层钢筋混凝土框架结构，总高60.6 m，首层高3.6 m，其余层高3 m，各层质量及水平侧移刚度见表2。结构阻尼比0.05，一阶模态振动周期2.849 6 s。要求选择10层安装等效阻尼系数ceq=2.1×107N·s/m的粘滞阻尼器，每层安装5个。为实现验证RFGA有效性及计算效率目的，选美国1940年5月18日Imperial Valley地震EL Centro地震波为输入，以各层最大层间位移角最小化为目标进行优化。据场地条件要求，将地震波峰值调整为400 gal。

采用本文所提RFGA与带精英保持策略的SGA分别进行10次优化。除适应度函数外， RFGA、SGA的控制参数完全相同，即种群规模N=60，最大进化代数T=100，交叉概率pc=0.8，变异概率pm=0.2。优化获得最优值为0.0077，最优解(最佳染色体)为[0 1 1 1 1 1 1 1 1 0 1 1 0 0 0 0 0 0 0 0]，即阻尼器最优布置位置为第2～9层与10～11层。不同优化算法对比见表3。由表3看出，RFGA经10次优化计算全部收敛于全局最优解；全局最优解所需目标函数平均计算次数为2 880次。带精英保持策略SGA经10次优化只5次收敛于全局最优解，其余5次未收敛或收敛于局部最优解；收敛于全局最优解的5次优化过程中，目标函数平均计算次数为3 276次。因此，RFGA的收敛速度与计算效率均优于SGA。

表2 各层质量及水平侧移刚度值

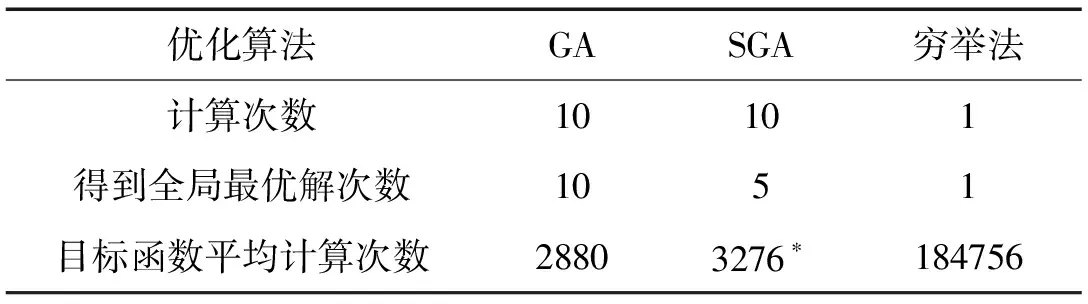
表3 RFGA、SGA与穷举法对比

注*：仅计入所得全局最优解的5次优化过程

最优布置方案与其它方案最大层间位移角对比见图1。用目标函数值代替适应度函数值优化曲线见图2。

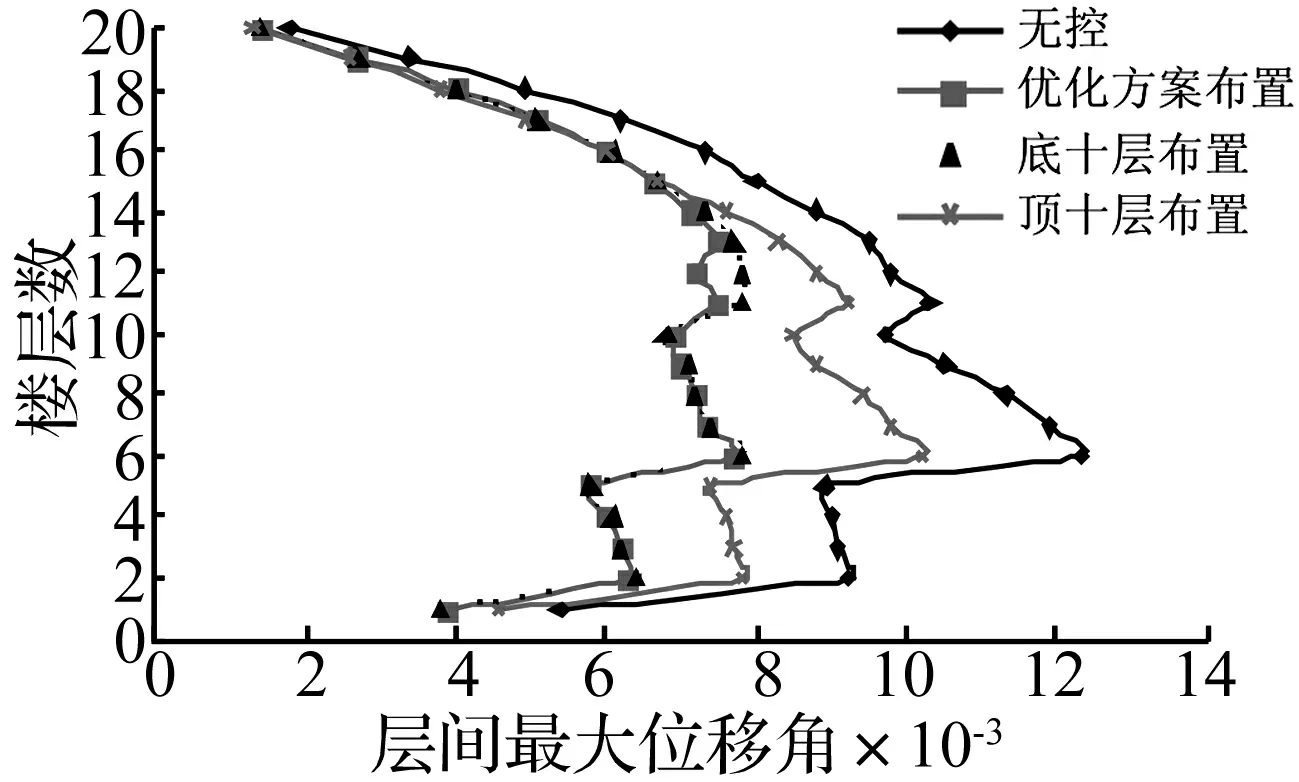
图1 楼层最大层间位移角包络图

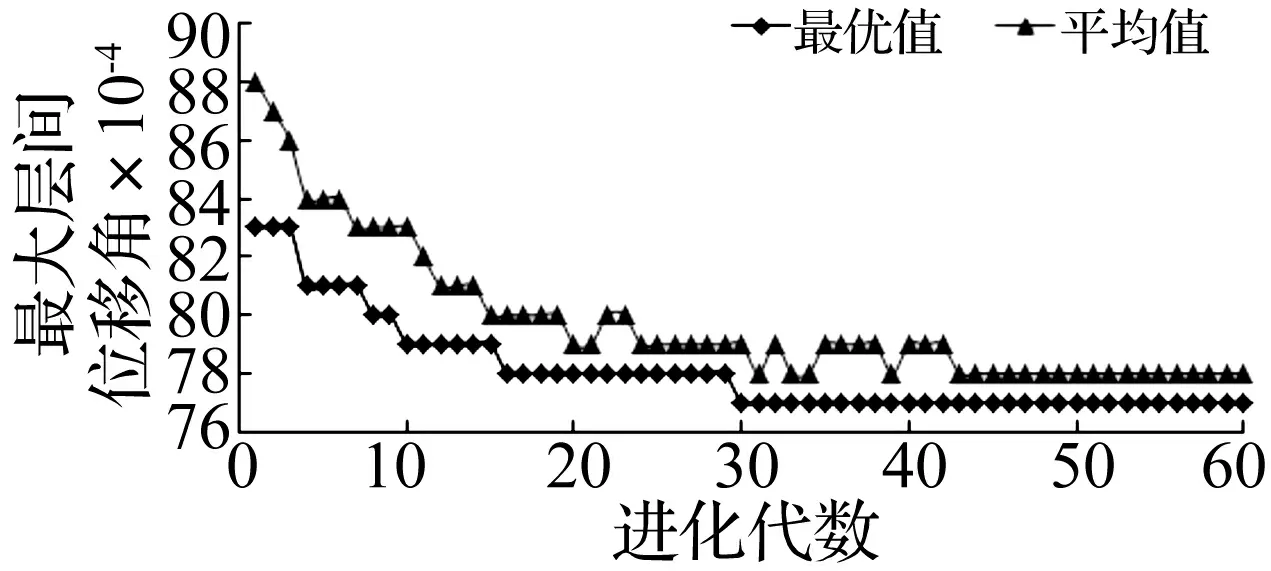
图2 优化曲线

3 目标函数讨论

3.1 不同加权系数组合优化结果

按文献[5-6]，式(4)的目标函数中，加权系数α,β,γ需据场地条件、阻尼器类型、建筑物结构特征及优化问题对安全性、舒适性不同要求给定。为探讨加权系数对优化结果影响，本文选EL Centro波(A波)、Tar Tarzana波(B波)、唐山波(C波)对加权系数不同的66种工况进行优化。据不考虑绝对最大位移(γ=0，β=1-α)与考虑绝对最大位移(γ=0.2，β=0.8-α)的不同，将优化结果分为两大类，见表4。由表4看出，① 是否考虑绝对最大位移对优化结果影响并不明显，超过半数的最优解完全相同；② 采用不同地震波响应，所得最优解有一定差异，但总体仍呈现随加速度权重的增大，阻尼器最优布置位置逐渐向中上层移动趋势；③ 最优解对权重系数变化不敏感，在EL Centro波作用下最明显，考虑绝对位移与不考虑绝对位移影响、α值分别在0.1～0.7与0.1～0.8范围内变化时，所得最优解完全相同。

表4 不同加权系数组合优化结果

注*：目标函数值相同的两个同最优解

考察不同地震波作用下单独以层间位移角、最大加速度、楼层位移为优化目标的减震系数，式(5)中θmax/θ0max，amax/a0max，umax/u0max取值下限，见表5。由表5看出，同一地震波下，各分项取值范围不同。如唐山波作用下，层间位移角项取值范围为[0.604 9,1.0]，加速度项取值范围为[0.801 0,1.0]，位移项取值范围为[0.624 3,1.0]。不同地震波作用下，同一分项取值范围也有所不同。同为位移项，在Tar Tarzana波作用下，取值范围缩小至[0.809 9,1.0]，区间长度仅为唐山波作用时的一半。

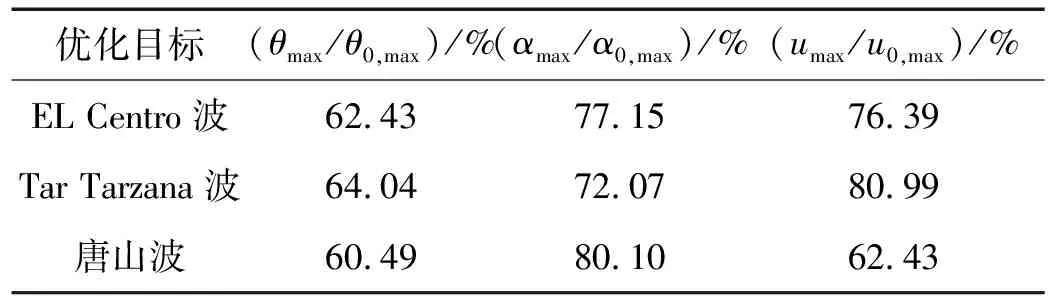
表5 减震系数

3.2 改进的目标函数公式

为使目标函数中各分项具备相同取值范围，本文据单独以层间位移角、最大加速度、楼层位移为优化目标所得优化结果，对式(4)中各项进行归一化处理，即：

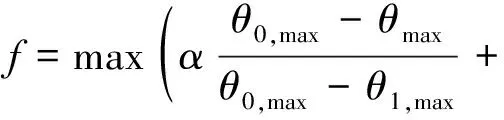
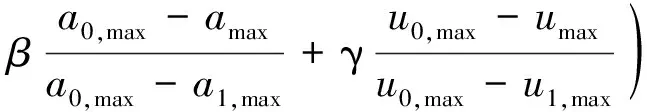
(8)

式中:下标0，max为无控结构响应最大值；1，max为仅以该项为目标优化所得结构响应最大值，需预先优化分析获得； max为当前阻尼器布置方案下结构响应最大值。

经归一化处理的各项数学意义为当前阻尼器配置方案的结构响应改进值与最大可能改进值间比值。由于式(4)采用相对改进率，使同一地震波作用下各分项已具备可比性，也使不同地震波下优化效果具有相同评价标准。在此基础上构造出考虑m条不同地震波作用的目标函数为：

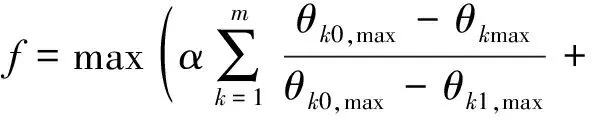
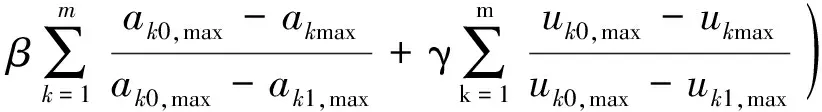
(9)

式中：下标k表示在第k条地震波作用下计算所得响应。

对工程中实际阻尼器优化布置问题，针对特定场地类型，可选择适用于该类场地的多条地震波进行优化，以满足结构设计需要。此外，由于式(8)、式(9)扩展了各分项的取值范围，会使加权系数α，β，γ的设定更具实际意义。优化结果对加权系数敏感性也有一定程度增强。

3.3 算例

用2.3节算例，选6种典型加权系数组合，以式(9)为目标函数，采用RFGA分析三种地震波作用下阻尼器最优配置方案。式(9)的目标函数取值越大，表示阻尼器布置方案减震效果越好。因此，采用RFGA时，需将式(7)改写为：

(10)

对每种加权系数组合分别进行4次计算。每次优化计算耗时约需1 800 s。所得阻尼器优化配置方案见表6，其中f1，f2，f3分别为最优方案在各地震波单独作用时的减震系数。由表6看出，同时考虑多条地震波作用所得最优解与单独考虑某条地震波所得最优解不同，充分说明式(9)考虑多条地震波作用优化意义。

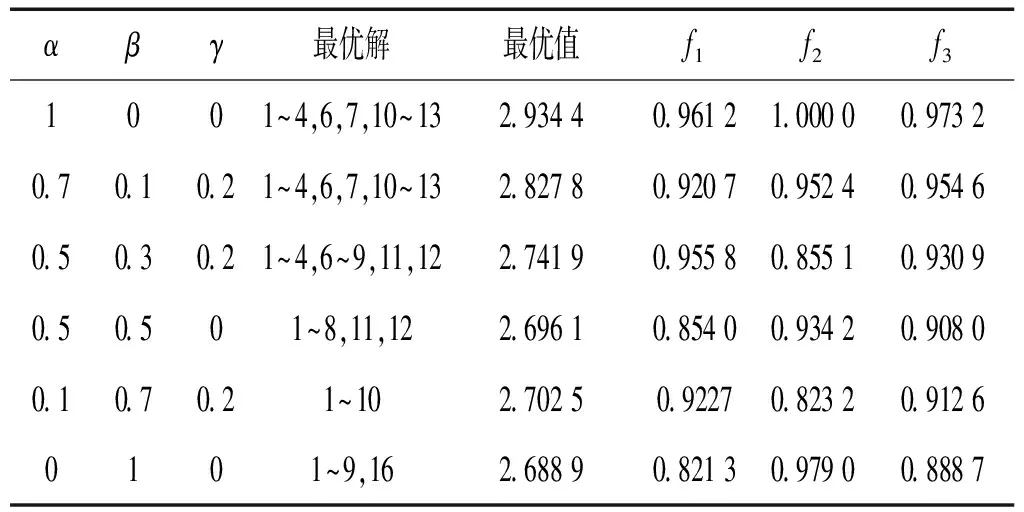
表6 加权系数组合及最优解

图3 计算流程图

需指出的是，虽本算例仅给出适合Ⅱ类场地的三条地震波优化计算结果，但式(9)的目标函数可适用于更多类型场地及任意数量的地震波。适用范围广泛，计算时间合理，且收敛于优化问题的全局最优解，为本文所提方法的主要优点。

3.4 计算流程图

基于相对适应度遗传算法的高层结构阻尼器优化配置方法计算流程见如图3。

4 结 论

(1) 对布置较多阻尼器的高层结构而言，优化问题设计空间所含可选优化方案数量巨大，用穷举法求解耗时过长甚至不能求解。较SGA，采用相对自由度方法构造适应度函数，能充分体现种群中染色体间适应度差异。优良染色体存活率大幅提高，有优良基因模式能以最合理概率存活，并通过交叉、变异等算子产生更优良模式，促进种群迅速进化，获得优化问题的全局最优解。

(2) 在深入探讨目标函数加权系数影响基础上，本文提出的改进目标函数计算式(8)，不仅使同一地震波作用下分项具备可比性，也使不同地震波下目标函数值具有相同评价标准。据此构造的多地震波条件下优化目标函数式(8)可用于分析不同场地、多条地震波作用时，不同目标函数加权系数组合的阻尼器优化布置方案。

参 考 文 献

[1]汪志昊，陈政清. 高层建筑结构中粘滞阻尼器的新型安装方式[J]. 世界地震工程,2010,26(4):135-140.

WANG Zhi-hao, CHEN Zheng-qing. New installations of viscous dampers in high rise buildings[J]. World Earthquake Engineering, 2010,26(4):135-140.

[2]XUE Xiao-min, SUN Qing, ZHANG Ling,et al. Journal of Intelligent Material Systems and Structures,2011,22(3): 291-302.

[3]Huang Z S, Wu C, Hsu D S. Semi-active fuzzy control of mr damper on structures by genetic algorithm[J]. Journal of Mechanics, 2009, 25(1): N1-N6.

[4]Mohebbi M, Joghataie A. Designing optimal tuned mass dampers for nonlinear frames by distributed genetic algorithms[J]. Structural Design of Tall and Special Buildings, 2012, 21(1):57-76.

[5]曲激婷. 位移型和速度型阻尼器减震对比研究及优化设计[D]. 大连：大连理工大学，2008.

[6]李宏男,曲激婷. 基于遗传算法的位移型与速度型阻尼器位置优化比较研究[J].计算力学学报,2010,27(2):252-257.

LI Hong-nan, QU Ji-ting. Comparison of optimal placement of displacement-based and velocity-based dampers using genetic algorithm[J]. Chinese Journal of Computational Mechanics, 2010,27(2):252-257.

[7]Li L, Song G, Ou J. A genetic algorithm-based two-phase design for optimal placement of semi-active dampers for nonlinear benchmark structure[J]. Journal of Vibration and Control,2010, 16(9):1379-1392.

[8]Oreski S,Oreski D,Oreski G. Hybrid system with genetic algorithm and artificial neural networks and its application to retail credit risk assessment[J]. Expert Systems With Applications, 2012, 39(16):12605-12617.

[9]燕乐纬,陈树辉,李 森,等. 一种改进的广义遗传算法及其在鲁棒优化问题中的应用[J].振动与冲击,2010,29(4):30-33.

YAN Le-wei,CHEN Shu-hui,LI Sen,et al. An improved generalized genetic algorithm and its application in robust optimization[J].Journal of Vibration and Shock, 2010, 29(4): 30-33.

[10]Su R K L, Yan L W. Provision of reinforcement in concrete solids using the generalized genetic algorithm[J].Journal of Computing in Civil Engineering,ASCE,2011,25(3):211-217.

[11]徐赵东，马乐为. 结构动力学 [M]. 北京：科学出版社，2007.

[12]玄光男，程润伟. 遗传算法与工程优化[M]. 北京：清华大学出版社，2004.

[13]Nakama T. Markov chain analysis of genetic algorithms applied to fitness functions perturbed concurrently by additive and multiplicative noise[J]. Computational Optimization and Applications,2012, 51(2):601-622.

[14]田 莉,陈换过,祝 俊. 基于自适应模拟退火遗传算法的传感器优化配置研究[J]. 振动工程学报，2012,25(3): 238-243.

TIAN Li, CHEN Huan-guo, ZHU Jun. A study of optimal sensor placement based on the improved adaptive simulated annealing genetic algorithm[J]. Journal of Vibration Engineering, 2012, 25(3):238-243.

[15]李敏强,寇纪淞,林 丹,等. 遗传算法的基本理论与应用[M]. 北京：科学出版社，2002.