考虑螺栓球节点半刚性的网格结构有限元模型修正研究
刘才玮, 张毅刚,2, 吴金志
(1. 北京工业大学 空间结构研究中心,北京 100124;2. 北京工业大学 城市与工程安全减灾省部共建教育部重点实验室,北京 100124)
健康监测已成为保证工程结构安全使用的有效手段。对重要结构的健康监测已有诸多研究。建立合理的有限元模型对研究结构动力特性是工程结构长期健康监测、状态评估基础[1],而据施工图纸建立的结构初始有限元模型含较多理想化信息或简化假定。由于空间网格结构复杂,自由度繁多、节点连接复杂、有限元离散化等因素必将导致按初始有限元模型计算的结构响应与实际结构存在一定偏差。因此为能对结构进行准确的模拟,需用理论及方法减小此差异,即对初始有限元模型进行修正。
传统的结构模型修正与基于模态分析的结构损伤识别方法在实际应用中均易受环境影响、模型依赖性强、系统容错性差等,而人工神经网络(Artificial Neural Networks,ANN)以良好的非线性映射能力、强大的解决反问题能力、实时计算及系统良好的鲁棒性在在工程应用中得到普遍重视[2]。Zapico等[3]利用两层前馈多层感知器(MLP)基于实测数据对小型钢结构框架进行模型修正。瞿伟廉等[4]建立基于径向基神经网络的空间网架结构有限元模型修正计算方法,并以具有13个球节点、32根杆件的焊接球节点网架为例,进行节点固结系数识别。但以节点固结系数表示的空间有限元模型建模较困难,试验模拟较复杂。刘晖等[5]以结构自振频率为输入,节点连接刚度参数为输出训练BP神经网络,试图使修正的焊接球节点网架结构有限元模型具有与实测结果一致自振频率,且应用于深圳市民中心网架结构有限元模型修正中。但由于未考虑振型因素影响,修正精度有待提高。何浩祥等[6]基于子结构建立以频率为输入、弹性模量为输出的神经网络递推模型修正法,并对单层球面网壳进行修正。但修正参数仅为杆件的弹性模量。考虑通常空间网格结构为钢结构,可近似认为杆件物理参数精确,主要需修正杆件端部节点连接刚度。
由于螺栓球节点加工制作工艺简单,现场安装方便,避免高空焊接作业,广泛应用于网格较规则的中、小跨度网架、双层网壳结构中[7-8]。螺栓球节点实质为典型的半刚性节点,设计中假设节点为铰接,即不考虑节点的抗弯刚度。此可能为动力测试结果与有限元分析结果不符的重要原因,但针对螺栓球节点的模型修正研究较少。张毅刚等[9]曾对具有157个节点、414根杆件的单层柱面网壳振动台试验模型的四种螺栓球节点进行精细化建模,利用摩擦系数、接触分析模拟高强螺栓与钢球之间的少许滑动,忽略销及预紧力影响,获得螺栓球连接弯矩-转角(M-θ)曲线。并将节点连接简化为惯性矩I与原杆件相同的节点单元,从而依据所得曲线确定节点单元弹性模量。经反复试算优选确定摩擦系数、接触参数,获得与Φ32×2.15、Φ48×3.5、Φ60×3.5、Φ89×3.75螺栓对应的四种节点单元
刚度折减系数分别为:0.524、0.466、0.317、0.122。由于空间网格结构节点种类繁多,过程较繁琐,不便于工程应用。本文在文献[9]基础上,避开螺栓球节点精细化建模时复杂参数的取值问题,利用单层柱面网壳试验模型实测频率及部分测点振型分量构造输入参数,采用广义回归神经网络 (GRNN)[10]对节点单元刚度折减系数分步修正,试图找到螺栓球节点模型修正新方法。
1 单层柱面网壳动力测试及相关性分析
单层柱面网壳振动台试验模型(以下简称试验网壳)纵向长21.0 m,宽3.0 m,矢高0.75 m,见图1。采用螺栓球节点,加大螺栓与套筒尺寸以增加连接处转动刚度。杆件类型分四种,对应四种套筒、螺栓,具体见表1。螺栓球节点型号BS180。该模型纵向有7个柱距,且每个柱距间结构杆件个数及类型相同或相似,螺栓球及杆件种类以第2个柱距(即第2跨)为例,见图2。在北京工业大学8个子振动台构成的台阵上进行试验,现场见图3。据数值模拟中试验网壳模态结果,传感器采用测点布置优先级综合排序方法进行布置[11],共44个加速度传感器,其中Y向与Z向各22个,见图4。动力特性测试采用正弦激振法。由于结构较长,利用两台50 N电磁激振器、DF1010超低频信号发生器及KD5701功率放大器,对该模型前四阶自振频率及前三阶振型进行测试。

图1 单层柱面网壳试验模型
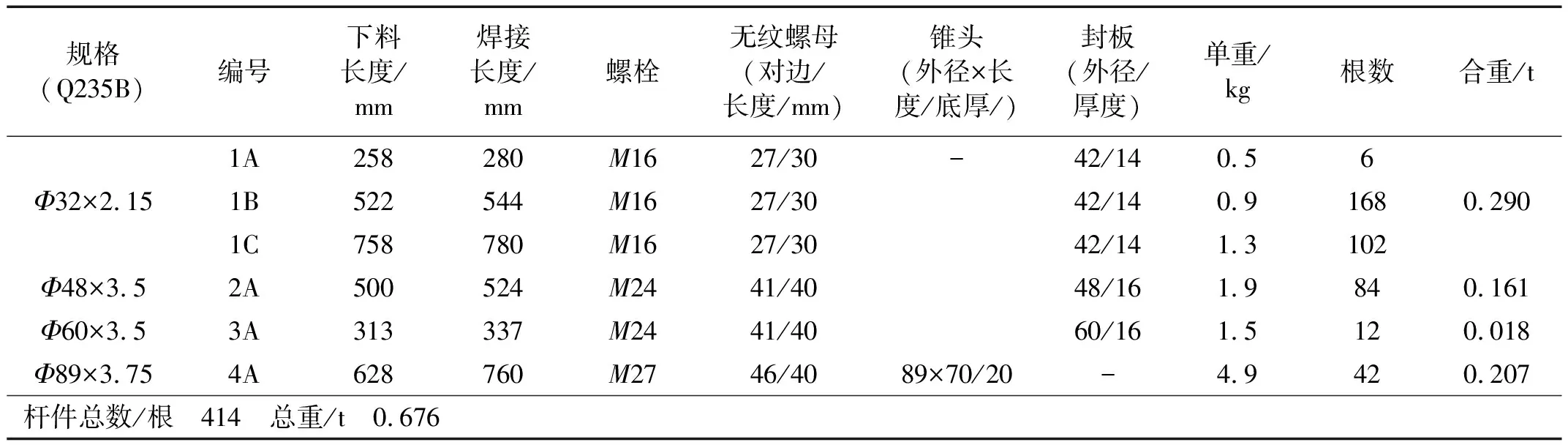
表1 杆件材料表

图2 螺栓球及杆件种类

图4 加速度传感器布置图
单层网壳工程设计中将球心至球心视为一根杆件,用梁单元模拟,节点视为刚接,本文称为刚性模型。为评价刚性模型的合理性,对其模态计算结果与实测模态数据进行相关性分析。设ωti=(i=1,2,…,n)表示实际测量自振频率;φti=(i=1,2,…,n)为实测振型;ωci=(i=1,2,…,n)为理论计算自振频率;φci=(i=1,2,…,n)为理论计算所得振型。采用参数衡量修正后模型优劣、频率变化率及模态置信准则分别定义为:
(1)
式(1)可度量第i阶自振频率及振型的优劣,ER(ωti,ωci)→0,MAC(φti,φci)→1说明修正结果好[12]。表2为试验网壳的频率实测值与刚性模型计算值对比,由表2可看出第二阶误差最小为16.58%。产生误差原因较多,如支座刚度、杆件及节点坐标偏差等,但刚性模型未合理考虑螺栓球节点的半刚性为主要原因。因此为获得较精确的数值模型,本文拟由螺栓球节点半刚性入手,对刚性模型进行有限元修正。
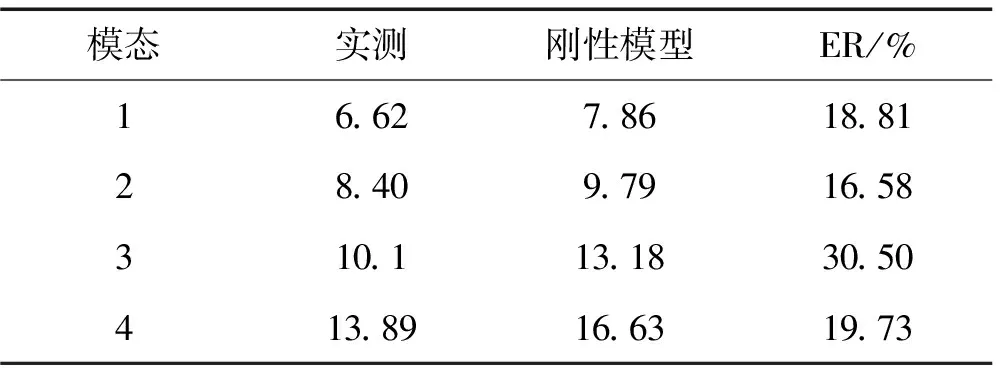
表2 频率实测值与有限元分析值对比(Hz)
2 考虑节点半刚性的螺栓球网格结构模型修正方法
2.1 半刚性模型建立
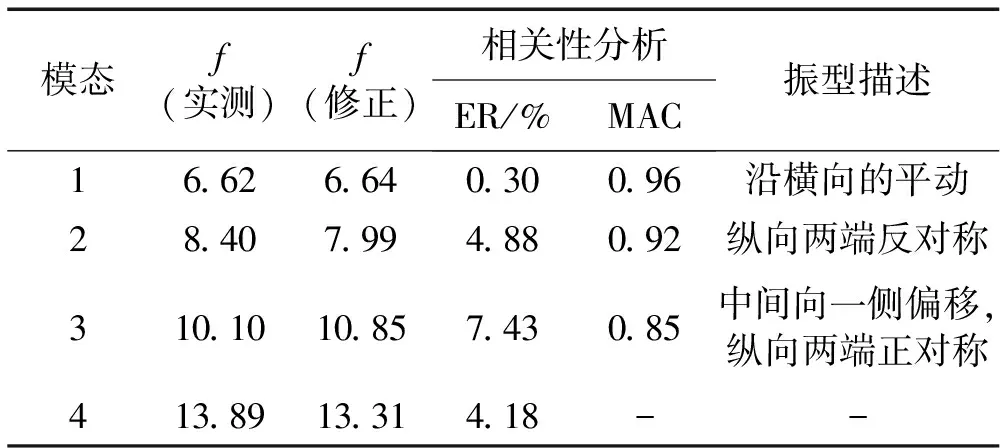
网格结构有限元模型准确关键取决于杆件与螺栓球节点连接方式的计算假设。本文建立刚度可调杆件单元模拟杆端节点连接,即螺栓球节点半刚性用具有刚度可调节点单元描述,称此模型为半刚性模型,见图5。其中L为节点单元长度;a为单元刚度折减系数(节点单元与杆件单元刚度比值),0 图5 刚度可调节点单元 空间网格结构有限元模型中参数众多,但每个参数对大型结构动力特性的敏感程度不同。因此在模型修正中,若考虑所有参数,不仅计算量大,计算时间长、效率低,且分析结果不易收敛。故应选反应敏感的参数作修正对象,而参数动力敏感性分析成为解决该问题的有效途径[13]。 试验网壳节点连接有四种类型,即:M16-32×2.15、M24-48×3.5、M24-60×3.5、M27-89×3.75。为获得其动力敏感性,以频率f1.0[9]考察节点单元刚度分别按0.9,0.95,1.05,1.1倍频率变化时fs为第s倍率时频率(s=0.9, 0.95, 1.05, 1.1),定义频率变化率计算公式为Δf=(fs-f1.0)/f1.0,计算结果见图6。由图6得:节点单元刚度分别变化时,M16-Φ32×2.15、M24-Φ48×3.5、M24-Φ60×3.5均对自振频率影响较大,而M27-Φ89×3.75的刚度变化对基频影响较小,其它阶频率规律与此类似。因此在修正时可不考虑M27-Φ89×3.75的影响,即节点单元刚度取值仍据文献[9]结果确定。 本文利用神经网络技术对M16-Φ32×2.15、M24-Φ48×3.5、M24-Φ60×3.5对应的三种螺栓球节点单元刚度折减系数进行修正。在文献[9]结果(a1=0.524,a2=0.466,a3=0.317)基础上,选a1=0.5,a2=0.45,a3=0.30(本文称为基准系数)为基准进行优化,以期找到更接近实际结构的折减系数。为此对修正参数容许变化范围限值,设定基准系数a1,a2,a3的允许变化区间为[-20%,20%],在此范围内寻优。 图6 不同节点连接类型刚度变化对基频影响 结构频率测试方便且较准确,能反应结构整体的动力特性。因此利用神经网络对结构修正时作为较好的输入参数[14]。但空间网格结构庞大,在结构损伤识别诊断时振型变化对损伤更敏感。针对空间网格结构特点,须合理运用两参数组合构造输入参数。修正后模型不仅要求频率接近,且应保证MAC值尽可能接近于1。本文采用频率与振型组合参数(Combined Parameters of Frequency and Mode,CPFM)为神经网络输入: CPFM={FRE1,FRE2,…,FREm;DF1,DF2,…,DFn} (2) 式中:m为所用频率阶数;n为所用振型阶数;FREi(i=1,2,…,m)为所用第i阶频率;DFi=(φi1,φi1,…,φiq,)为第i阶模态对应q个测试自由度归一化振型向量,计算式为: (3) 式中:φij为第i阶模态对应于j个测试自由度分量。 据空间网格结构实际工程及试验网壳模态测试经验,为保证实测数据的有效性,构造参数CPFM时原则上规定频率不宜超过前五阶(m≤5)、振型不宜超过前三阶(n≤3),且尽量选此范围内振动形式较简单阶次。 图7 修正方法流程图 综上分析,考虑节点半刚性螺栓球网格结构模型修正流程见图7。按图7,以a1=0.5,a2= 0.45,a3=0.30为基准系数,据以上提出的分步修正策略,通过试验网壳半刚性模型建立组合参数CPFM与节点单元刚度折减系数关系样本库A、B,再通过训练GRNN(即以组合参数CPFM为输入,结构节点单元刚度折减系数为输出),最终可得试验网壳节点单元折减系数识别的逆向神经网络模型。将实测的前四阶频率与一、二阶Y、Z向9个位置(图1中黑色实心圆)18个传感器振型分量构造CPFM(40×1矩阵)为GRNN网络输入,二次修正后的刚度折减系数为[0.594,0.536,0.241],代入试验网壳半刚性模型进行模态计算,结果与实测值分析见表3。由表3看出: (1) 与表2相比,各阶次频率误差均有大幅度减小,且第一阶振型符合良好,反映结构真实动力特性较准确,证明本文所用修正方法合理有效。 表3 模型修正结果 (2) 因空间网格结构自身庞大、激励能量有限导致低阶模态易被激发,且一阶振型为简单平动,测试结果较符合;三阶振型较复杂,输入参数未考虑三阶振型影响,导致修正后三阶模态误差较大。 (3) 修正后仍存在误差,原因如假设杆件几何尺寸、材料弹性参数均可精确获得因而未考虑动力敏感度低的M27-Φ89 ×3.75刚度修正;试验中也存在加工、安装精度等误差及测试环境干扰。 本文基于实测模态数据对试验网壳进行有限元模型修正研究,结论如下: (1) 提出的建立带有刚度可调节点单元的半刚性模型对螺栓球节点单元刚度折减系数进行有限元模型修正新方法,通过试验网壳模型修正,该方法有效性得以验证。与传统矩阵型、参数型修正方法相比,该方法物理意义明确、计算量小、精度高。 (2) 针对空间网格结构节点、杆件众多等特点,所用分步修正策略可效避免神经网络的数据爆炸及非线性能力降低等问题,可增强其在空间网格结构中的适用性。 (3)对实际工程监测中布置测点有限问题,用结构有限测点低阶频率及振型分量构造神经网络输入参数CPFM,通过试验网壳模型修正证明其有效性。本文所提修正方法适合于不完备的模态数据,具有一定工程应用价值。 参 考 文 献 [1]OU Jin-ping, LI Hui. Structural health monitoring in mainland China: review and future trends[J]. Structural Health Monitoring,2010,9(3):219-231. [2]Samali B, Dackermann U, Li J C. Ocation and severity identification of notch-type damage in a two-storey steel framed structure utilising frequency response functions and artificial neural network[J]. Advances in Structural Engineering , 2012, 15 (5) :743-757. [3]Zapico J L, González-Buelga A, González M P, et al. Finite element model updating of a small steel frame using neural networks[J].Smart Materials and Structures, 2008, 17(4): 045016-045027. [4]瞿伟廉, 谭冬梅, 汪 箐, 等. 基于神经网络的大型空间网架结构的有限元模型修正[J]. 地震工程与工程振动,2003,23(4):83-89. QU Wei-lian, TAN Dong-mei, WANG Jing, et al. Finite element model correction of large space truss structure based on neural net[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(4): 83-89. [5]刘 晖, 瞿伟廉, 王锦文, 等. 基于有限测点信息的大型空间网架结构智能工作状态评估技术研究[J]. 土木工程学报, 2007, 40(12): 52-58. LIU Hui, QU Wei-lian, WANG Jin-wen, et al. A study on estimation of the intelligent work status of large space truss structures based on limited measurement information[J]. China Civil Engineering Journal,2007, 40(12): 52-58. [6]何浩祥, 闫维明, 王 卓. 基于子结构和遗传神经网络的递推模型修正方法[J]. 工程力学, 2008,25(4):99-105. HE Hao-xiang,YAN Wei-ming,WANG Zhuo. Stepwise model updating method based on substructures and GA-ANN[J]. Engineering Mechanics, 2008, 25(4):99-105. [6]蔡艳平,李艾华,石林锁.基于盲解卷积的柴油机振动信号的分离研究[J].振动与冲击,2010,29(9): 38-41,240. CAI Yan-ping,LI Ai-hua,SHI lin-suo.Separation of diesel engine vibration signals based on the blind deconvolution[J].Journal of Vibration and Shock, 2010,29(9):38-41,240. [7]周晓峰,杨世锡,甘春标.相关机械振源的盲源分离方法[J].振动与冲击,2012,31(14):60-63. ZHOU Xiao-feng,YANG Shi-xi,GAN Chun-biao. Blind source separation of statistically correlated sources[J].Journal of Vibration and Shock, 2012, 31(14):60-63. [8]Comon P.Independent compoment analysis ,a new concept[J].Signal Processing, 1994,36(3):287-314. [9]Zhukov L,Weinstein D,Johnson C.Indepentent component analysis for EEG source location[J]. IEEE Engineering in Medicine and Biology Magazine,2000,19(3):87-96. [10]Hyvärinen A, Karhinen J, Oja E. Independent component analysis[M]. New York:Wiley,Chichester,2001. [11]GrayW C.Variablenom deconvolution[D]. Standford:PhD Dissertation of Stanford, 1979. [12]Choi S, Cichocki A.On-line sequential multichannel blind deconvolution:a deflation approach[C].Proceedings of the 8th IEEE DSP Workshop,Utath,USA,1998:159-162. [13]Liu X H,Robert B R, J r me A.Blind separation of internal combustion engine vibration signals by a deflation method[J].Mechanical Systems and Signal Processing,2008,22(5):1082-1091 . [14]Liu X H, Robert B R.Blind source separation of internal combustion engine pistion slap from other measured vibration signals[J].Mechianical Systems and Singal Processing, 2005, 19(6): 1196-1208. [15]Hao Zhi-yong, JIN Yan,YANG Chen.Study of engine noise based on independent component analysis[J]. Zhejiang University Science A,2007,8(5):772-777. [16]Jerome A.Blind separation of vibration components:principles and demonstrations[J]. Mechanical Systems and Singal Processing, 2005,19(6):1166-1180.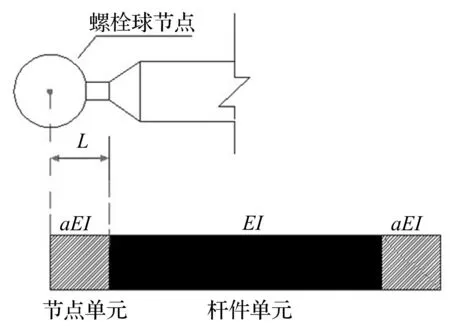
2.2 修正参数确定
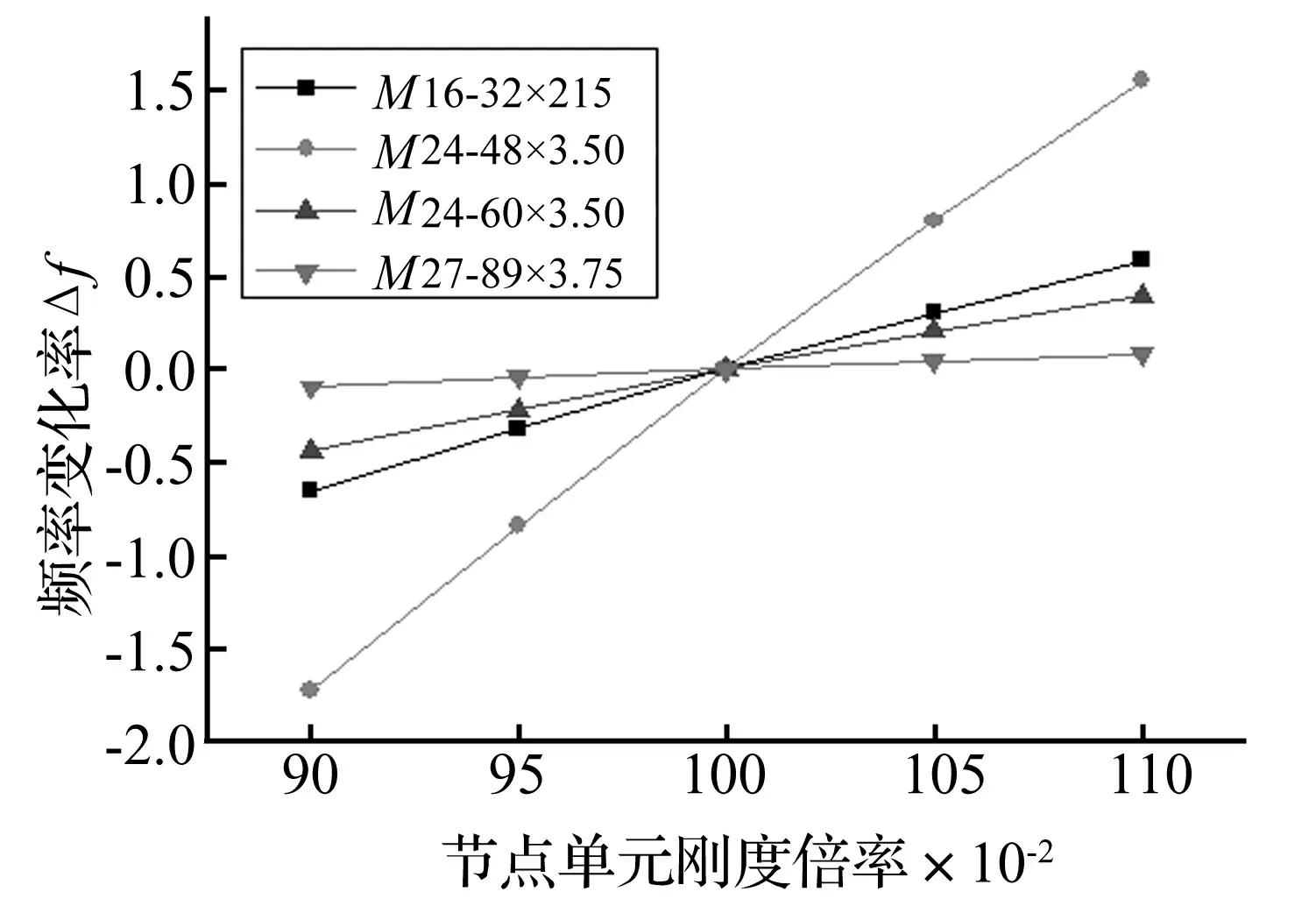
2.3 神经网络输入参数确定
2.4 基于GRNN网络的分步修正策略
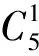
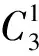
3 基于实测数据的试验网壳模型修正

4 结 论

