大型地下厂房开挖爆破振动动力响应数值模拟
姚 强, 杨兴国, 陈兴泽, 李洪涛
(1. 四川大学 水力学与山区河流开发保护国家重点实验室, 成都 610065;2. 四川大学 水利水电学院, 成都 610065;3. 国电大渡河流域水电开发有限公司, 成都 610041)
我国水电资源大多分布于西部深山狭谷中,位于该地区的水电工程,采用地下厂房形式有利于枢纽布置与拦河大坝快速施工。作为大型地下洞室工程,地下厂房不仅跨度大、边墙高,且结构复杂,对施工质量要求较高,目前普遍采用钻爆法施工。钻爆法在完成厂房开挖的同时,诱发的爆破振动效应会引起保留围岩力学性质劣化,过大爆破振动亦会导致地下厂房岩锚梁混凝土开裂、混凝土与岩石间粘结力损失等[1],甚至导致围岩局部坍塌及失稳,安全事故时有发生。
钻爆法开挖诱发的地震波对地下厂房结构稳定影响较大。王玉杰等[2]回归分析过周宁水电站地下厂房爆破地震波的衰减规律;严鹏等[3]通过分析爆破过程中开挖边界初始地应力动态卸载过程研究初始地应力场对围岩振动影响;陈明等[4]利用数值模拟研究爆破振动荷载作用的地下厂房岩锚梁动态响应特性;蒋耀港等[5-6]对拆除爆破引起的塌落振动及城市复杂环境下爆破振动危害效应进行理论及监测研究。但目前针对复杂条件下大型地下厂房爆破振动荷载作用的空间动力响应研究并不多见,对爆破地震波在厂房中的传播规律、危害大小及控制标准等还尚无明确认识,需进一步研究。
向家坝水电站主厂房跨度31.4 m,高88.2 m,规模属世界前列,且工程地质条件复杂,被多条断层及软弱夹层影响,节理裂隙发育,而开挖过程中稳定性为控制工程安全的重要因素。本文借助动力有限元软件ANSYS/LS-DYNA进行数值模拟,研究该厂房在爆破振动荷载作用下动力响应,分析顶拱、岩锚梁及高边墙等重点部位爆破振动衰减规律与应力分布,获得爆破振动荷载作用下易发生破坏、施工中应重点监测及保护部位。在综合分析数值计算结果与大量爆破振动监测数据基础上,给出的建议采用爆破振动安全控制标准,可为类似工程提供参考。
1 爆破荷载施加方法
爆破荷载数值模拟主要有3种方法:①直接模拟法,用有限元程序中炸药材料及状态方程控制炸药的爆轰过程;②确定作用于炮孔壁的爆轰压力峰值及时程曲线,并将该半理论半经验爆破荷载时程曲线施加于炮孔壁;③建模时不考虑炮孔形状,对爆破荷载按一定方法等效,将等效后爆破荷载时程曲线施加于同排炮孔连线,作用范围与炮孔内装药段长度相等[7]。直接模拟法适用于模拟近区冲击响应,后两种方法则适用于中远区爆破振动数值模拟。由于炮孔尺寸远小于工程岩体尺寸,因用前两种方法建模时需体现出炮孔,给模型建立及网格划分造成困难,计算量巨大,为省去繁杂的网格划分,本文采用施加等效荷载方法。该方法关键在于确定爆破荷载模型、爆破荷载峰值及作用时间,对其等效后施加于模型。目前工程中常用爆破荷载衰减模型主要有三角形分布模型与半理论半经验指数函数分布模型。本文采用三角形荷载模型,使用时需确定爆破荷载峰值P0,爆破荷载升压时间t1及正压作用时间t2。
确定爆破荷载峰值P0,据凝聚炸药爆轰波C-J理论,对耦合装药,炮孔初始平均爆轰压力P0为波阵面后最大压力的一半:
(1)
式中:P0为炸药爆轰平均初始压力;ρe为炸药密度;D为爆轰速度;γ为炸药等熵指数,取γ=3。
对不耦合装药条件,装药不耦合系数较小时,爆生气体膨胀只经过P>Pk状态,炮孔初始平均压力P0计算式为:
(2)
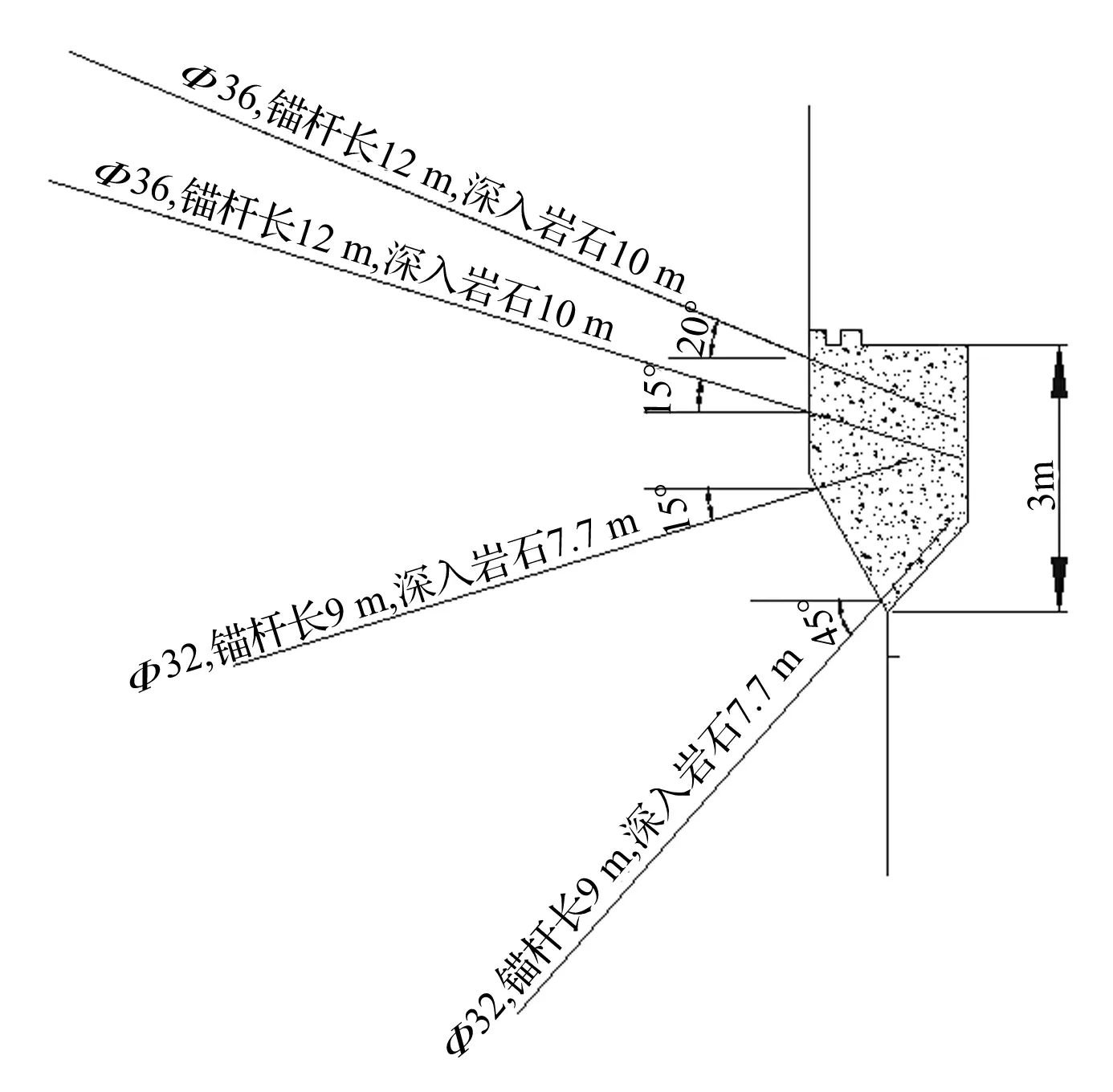
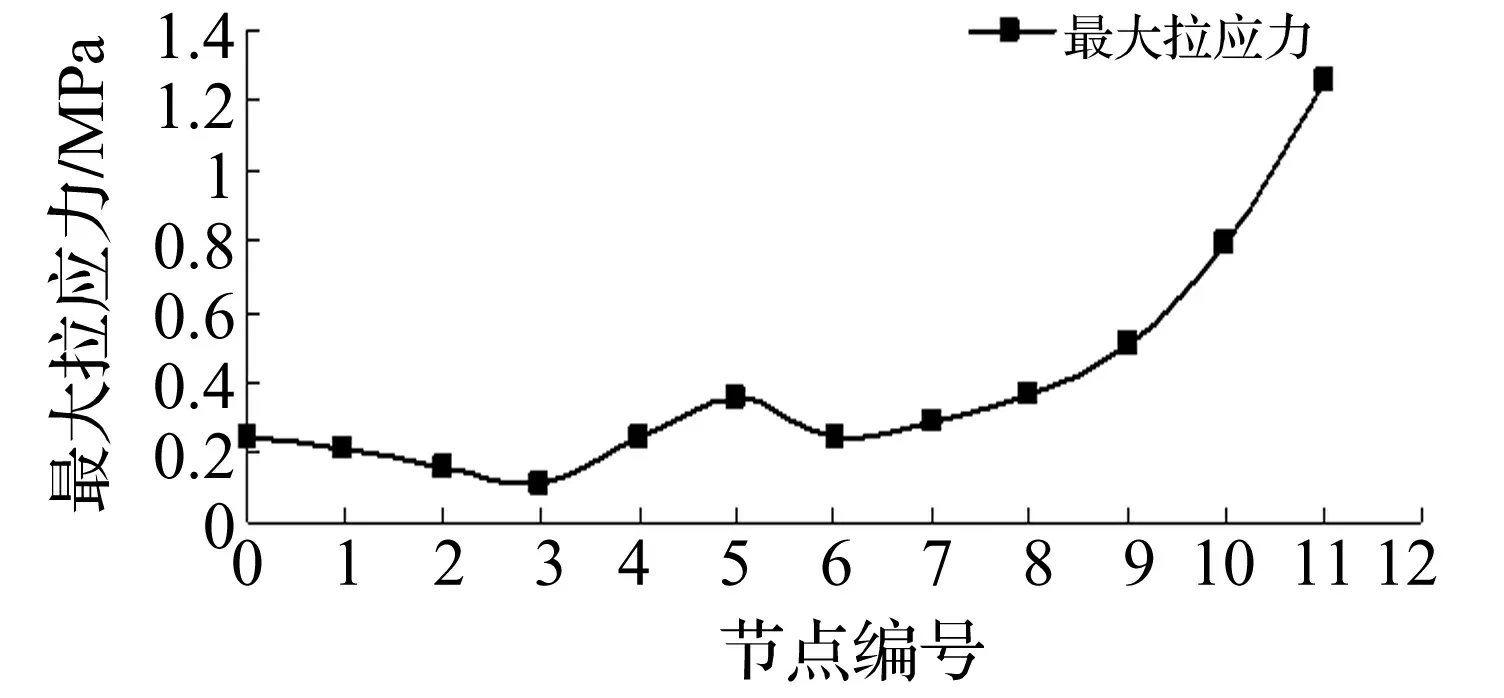
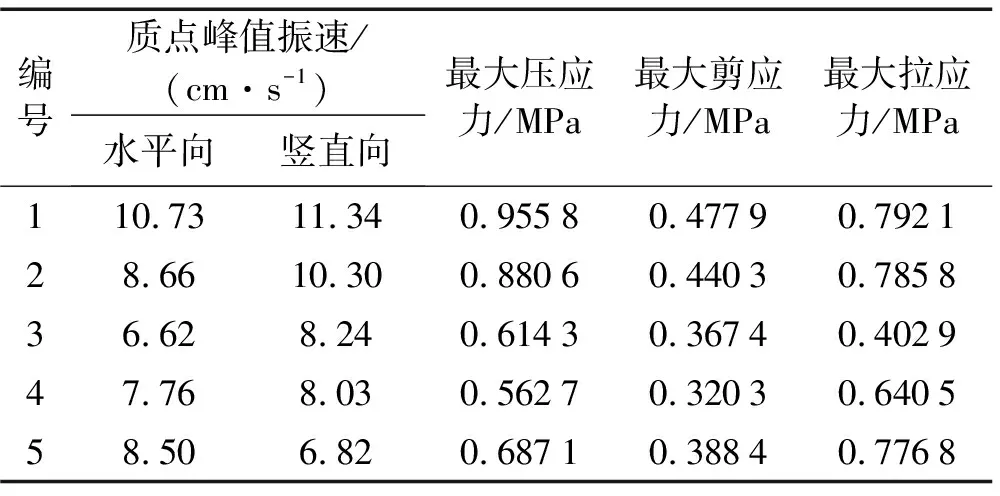
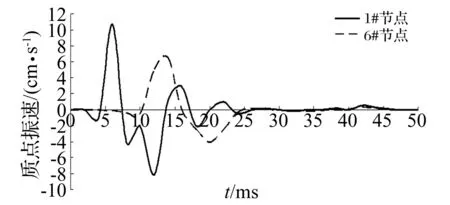
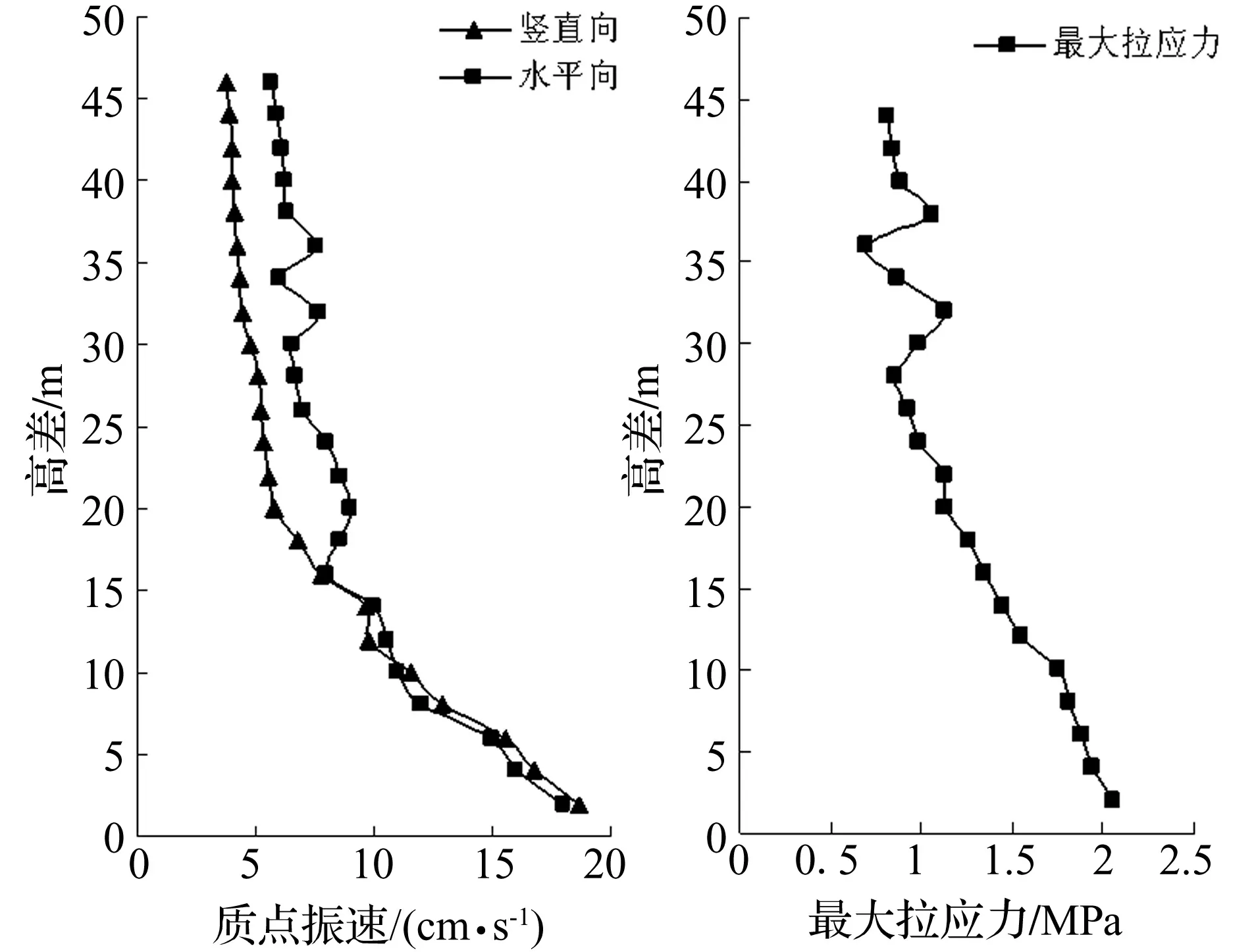
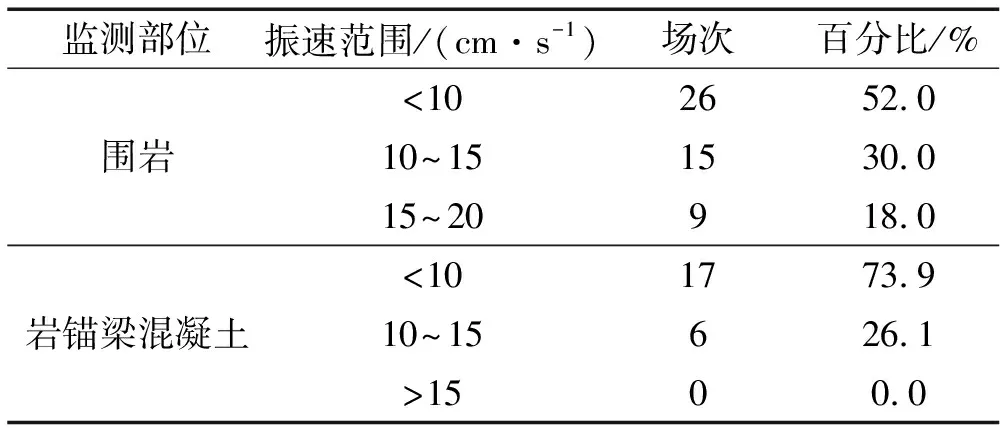
装药不耦合系数较大时,爆生气体膨胀需经历P≥Pk及P (3) 式中:P0为不耦合装药时爆破荷载峰值压力;ν为膨胀绝热指数,ν=1.2;dc为装药直径;db为炮孔直径。本工程中用2#岩石硝铵炸药:密度1 000 kg/m3;爆轰波速3 600 m/s;气体临界压力Pk=200 MPa。 图1 爆破荷载等效施加方法 荷载等效施加方法见图1,设单个炮孔壁上作用压力P0,炮孔半径r0,孔间距a,考虑力、力矩的平衡,将作用于炮孔壁压力(图1(a))等效施加于炮孔连心线(图2(b)),施加等效压力值算式为: Pe=(2r0/a)P0 (4) 据研究成果[1,7-10],本文取正压作用时间t2=400 μs,升压时间t1=100 μs,爆破荷载过程曲线见图2。 图2 爆破等效动荷载时程三角形分布 材料采用理想弹塑性模型,据Cowper-Symonds方程考虑应变率效应,即: (5) (6) 式中:E为材料弹性模量;Etan为切线模量。 数值模拟材料参数见表1。岩石动强度一般为静强度的1.2~5倍,在冲击荷载作用下,软岩动抗压强度及动弹性模量甚至高于静载近10倍[11]。故在爆破振动荷载作用下须考虑材料动强度与静强度差别,本文设围岩及混凝土动抗拉强度均提高2倍,即5 MPa,3 MPa。 表1 材料参数 向家坝水电站主厂房分Ⅸ层开挖。第Ⅰ层开挖高度11.2 m,开挖程序为中部导洞开挖、上游侧扩挖及下游侧扩挖。第Ⅱ层开挖高度7 m,开挖程序为中部拉槽及两侧保护层开挖。第Ⅲ层为岩锚梁所在分层,高9 m,开挖程序为中部拉槽、两侧保护层及岩台开挖。第Ⅳ~Ⅶ层层高分别为8.5 m、10.5 m、9 m、8 m,均用先两侧边墙预裂、中部拉槽跟进、深孔梯段爆破的开挖方式。主厂房第Ⅷ、Ⅸ层开挖层高11.5 m,13.38 m,均分三小层开挖。据地下厂房开挖程序,厂房第Ⅱ层紧接顶拱层开挖,且开挖爆破规模大,引起顶拱层爆破振动响应最大;刚浇注成型的岩锚梁对第Ⅳ层爆破开挖诱发的振动响应最大,岩锚梁局部断面见图3。第Ⅶ层爆破开挖时高边墙已形成,且第Ⅶ层爆破规模较下两层大,高边墙对第Ⅶ层爆破振动响应最大。故分别建立第Ⅱ层、第Ⅳ层、第Ⅶ层计算模型,分析顶拱、岩锚梁、高边墙的爆破振动响应。 图3 向家坝地下厂房岩锚梁结构断面图 第Ⅱ层计算模型宽150 m,高100 m,四周用无反射边界,见图4。第Ⅱ层开挖时中部拉槽梯段爆破孔深、孔径、最大单响药量及爆破规模均最大,故对梯段爆破进行数值模拟。梯段爆破炮孔径76 mm,药径60 mm,孔深7.6 m,孔距1.95 m,堵塞长度1.0 m。因装药不耦合系数较小,按式(2)计算爆破荷载峰值压力P0=392.2 MPa,据式(4)得等效荷载Pe=15.3 MPa。 第Ⅳ层计算模型宽150 m,高130 m,四周用无反射边界,见图5。开挖时预裂爆破靠近保留边墙及岩锚梁,且孔深、最大单响药量及受岩石夹制作用较大, 爆破时对岩锚梁影响大,故对预裂爆破进行数值模拟。预裂爆破孔径80 mm,药径25 mm,孔深9.0 m,孔距0.7 m,堵塞长度0.7 m。装药不耦合系数较大,据式(3)得爆破荷载峰值Pm=180.6 MPa,据式(4)得等效荷载Pe=20.6 MPa。 图4 第Ⅱ层计算模型 第Ⅶ层计算模型高宽均150 m,四周用无反射边界,见图6。开挖情况与第Ⅳ层相似,亦对预裂爆破进行模拟。预裂爆破孔径80 mm,药径32 mm,孔深10.5 m,孔距0.7 m,堵塞长度0.7 m。装药不耦合系数较大,据式(3)计算爆破荷载峰值压力为Pm=326.7 MPa,据式(4)计算等效荷载Pe=37.3 MPa。 模拟第Ⅱ层中部拉槽爆破时,从顶拱拱脚向上至拱顶依次选编号0~11共12节点,各质点峰值振速见图7。由图7看出,顶拱拱脚处水平向及竖直向质点峰值振速最大,为8.5 cm/s,8.1 cm/s,质点峰值振速沿拱脚向上迅速衰减,拱顶质点振速最小。 图7 顶拱各点峰值质点振速 混凝土与岩石抗压强度远大于抗拉强度,抗剪强度亦高于抗拉强度,故按极限拉应力准则判断围岩及岩锚梁破坏。顶拱围岩最大拉应力计算结果见图8。由图8看出,拱脚处拉应力最大为1.26 MPa,由拱脚至拱顶拉应力迅速衰减,与质点峰值振速变化规律相似。第Ⅱ层中部拉槽爆破引起围岩最大拉应力小于岩石动抗拉强度,不会造成围岩破坏。 图8 顶拱各点最大拉应力 岩锚梁与岩石胶结体强度最薄弱处为黏结面,因其强度较低,较易发生破坏。故应重点关注黏结面响应。模拟厂房第Ⅳ层预裂爆破时,由岩锚梁黏结面底部向上取1~5编号5个节点,各点质点峰值振速与应力计算结果见表2。由表2看出,竖直向质点峰值振速在黏结面底部最大,为11.34 cm/s,向上快速衰减。水平向质点峰值振速在黏结面底部最大,为10.73 cm/s,向上先减小后增大,变化较复杂。岩锚梁黏结面最大压应力与最大拉应力水平相当,而最大剪应力则小很多。黏结面顶部或底部拉应力均可能最大,为0.7921 MPa,而混凝土与岩石黏结面抗拉强度试验值大于1.0 MPa,故黏结面是安全的。黏结面最大拉应力与水平向质点振速分布规律相似,黏结面破坏受水平向控制,安全质点振速受水平向质点振速控制。 将黏结面底部节点1与边墙上节点6质点振速时程曲线进行比较,见图9、图10。由两图看出,点1水平向质点振速时程曲线较点6复杂,竖直方向相似。其原因由于岩锚梁黏结面为混凝土与岩石两种材料交界处结构体型复杂,导致应力波在传播过程中发生折射与反射,使黏结面质点振速曲线复杂化。 表2 爆破振动作用下岩锚梁动力响应计算结果 图9 水平向质点振速时程曲线 图10 竖直向质点振速时程曲线 模拟第Ⅶ层爆破开挖计算的边墙各点峰值振速及最大拉应力随高差变化曲线见图11。由图11看出,各方向质点峰值振速随高程增加而减小。距爆源15 m高差范围内,各方向质点峰值振速数值大小与衰减规律相似,且衰减较快。超过15 m后,竖直向振速衰减幅度明显大于水平向,各点振速小于水平向。由于岩锚梁的存在,水平向振速出现反射与折射,距爆源高差35 m处岩锚梁区域水平向质点峰值振速出现波动,影响范围局限于岩锚梁附近。 图11 质点峰值振速及最大拉应力随高程变化曲线 在水电工程施工过程中,评价爆破振动危害效应为控制距爆源10 m处质点峰值振速。距离爆源10 m高差处计算边墙水平向质点峰值振速为11.24 cm/s,竖直向为11.63 cm/s。边墙最大拉应力随高程增加而减小,变化较均匀。最大拉应力距爆源10 m高差处为1.75 MPa,小于岩石动抗拉强度,围岩不会发生破坏。在岩锚梁影响区内的最大拉应力出现波动,与水平向质点峰值振速相关性较好。据数值计算结果,各部位安全质点振速计算式为: (7) 式中:σd为动抗拉强度;σ为最大拉应力;ν为质点峰值振速。据式(7)得拱脚、岩锚梁黏结面及距爆源10 m高差处边墙的安全质点振速分别为33.7 cm/s、13.55 cm/s、32.1 cm/s。考虑2倍安全系数,得安全质点振速分别为16.8 cm/s、6.8 cm/s、16.0 cm/s。据计算结果,岩锚梁及围岩安全质点振速可分别取不大于7.0 cm/s及16.0 cm/s。 爆破安全规程(GB6722-2003)中规定水工隧道的爆破振动安全允许标准为7~15 cm/s,7~28 d龄期混凝土为7.0~12 cm/s。向家坝水电站工程招标文件则要求围岩及7~28 d龄期混凝土安全质点振速分别为10 cm/s及5.0~7.0 cm/s。本文对向家坝水电站地下厂房开挖过程进行大量爆破振动监测,围岩及岩锚梁部位实测质点峰值振速结果见表3。由表3看出,围岩实测质点振速有多个场次达到10~15 cm/s,甚至达到15~20 cm/s;岩锚梁处实测质点振速有多个场次达到10~15 cm/s,均只有约50%监测数据满足工程招标文件要求。据爆破施工后现场调查,即使爆破振动出现多次超标,围岩及岩锚梁混凝土亦未发生明显破坏,在一定程度上说明工程招标文件对爆破振动控制规定偏严格。 由于岩锚梁并非每点均达最大质点振速及最大拉应力,且岩锚梁黏结面抗拉强度取静态强度较小值1.0 MPa,未考虑动态条件材料强度的提高。而本文数值模拟时采用过假定,计算模型亦有简化,综合分析计算结果与现场监测,参考《爆破安全规程》规定,建议围岩及混凝土龄期超过28 d的岩锚梁安全质点振速分别为不大于15.0 cm/s,10.0 cm/s。据本文建议的控制标准控制爆破振动,表3中监测数据约80%均符合要求,且实际不会对厂房结构造成破坏,可为类似工程提供参考。 表3 围岩、岩锚梁实测最大振速统计 通过数值模拟、现场监测,分析向家坝水电站地下厂房开挖中爆破振动响应特性,结论如下: (1)在地下厂房开挖爆破振动荷载作用下,顶拱拱脚处质点振速及拉应力最大,岩锚梁黏结面顶部或底部拉应力最大,黏结面安全受水平向质点峰值振速控制。水平向应力波在岩锚梁黏结面发生反射、折射等现象。 (2)由于实测的围岩、岩锚梁质点峰值振速分别达15~20 cm/s与10~15 cm/s而未产生破坏现象,故综合数值计算、爆破振动监测结果,建议围岩、混凝土龄期超过28天的岩锚梁安全质点振速分别取不大于15.0 cm/s与10.0cm/s,且有一定安全储备。 (3)爆破振动频率、地下厂房大小、围岩性质及埋深等因素不同,爆破施工诱发的振动对地下厂房影响大小不同,爆破振动控制标准亦不同,需分别研究。 参 考 文 献 [1]张文煊. 大型地下厂房开挖爆破振动破坏特性研究[D].合肥: 中国科学技术大学, 2008. [2]王玉杰,梁开水,田新邦.周宁水电站地下厂房开挖爆破地震波衰减规律的研究[J].岩石力学与工程学报,2005,24(20): 4111-4114. WANG Yu-jie, LIANG Kai-shui, TIAN Xin-bang. Study on redundant regulation of underground digging blasting vibration of zhouning hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(20):4111-4114. [3]严 鹏,卢文波,陈 明.初始地应力场对钻爆开挖过程中围岩振动的影响研究[J]. 岩石力学与工程学报, 2008, 27(5): 1036-1044. YAN Peng, LU Wen-bo, CHEN Ming. Study on impaction of initial geostress field on vibration of surrounding rock during excavation with drilling and blasting[J]. Chinese Journal of Rock Mechanics and Engineering, 2008,27(5):1036-1044. [4]陈 明,卢文波,易长平.大型地下厂房岩锚梁爆破安全控制标准研究[J]. 岩石力学与工程学报,2006,25(3):499-504. CHEN Ming, LU Wen-bo, YI Chang-ping. Research on safety standard for rock anchor beam under blasting vibration in large undergroud powerhouse[J]. Chinese Journal of Rock Mechanics and Engineering, 2006,25(3):499-504. [5]蒋耀港,沈兆武,龚志刚.构筑物爆破拆除振动规律的研究[J].振动与冲击,2012,31(5):36-41. JIANG Yao-gang,SHEN Zhao-wu,GONG Zhi-gang.Vibration law of structure blasting demolition[J].Journal of Vibration and Shock,2012,31(5):36-41. [6]蒋耀港,沈兆武,杨昌德.市内复杂环境下大药量爆破降振及振动监测分析的研究[J].振动与冲击,2012,31(1):156-161. JIANG Yao-gang,SHEN Zhao-wu,YANG Chang-de.Big charge blasting vibration damping and vibration monitoring analysis under intracity complicated environment[J].Journal of Vibration and Shock,2012,31(1):156-161. [7]许红涛. 岩石高边坡爆破动力稳定性研究[D]. 武汉: 武汉大学, 2006. [8]卢文波, 陶振宇. 预裂爆破中炮孔压力变化历程的理论分析[J]. 爆炸与冲击,1994, 14(2):140-147. LU Wen-bo, TAO Zhen-yu. Theoretical analysis of the pressure variation in borehole for pre-splitting explosion[J]. Explosion and Shock Waves, 1994, 14(2):140-147. [9]黄玉锋, 舒大强, 陈维炎. 爆破震动作用下地下洞室支护结构的动态响应分析[J].爆破,2006,23(1):14-18. HUANG Yu-feng, SHU Da-qiang, CHEN Wei-yan. Effect of blasting vibration on the support structure of an underground chamber[J]. Blasting, 2006,23(1):14-18. [10]张建华, 李世禄, 王玉杰. 爆炸扩腔数值模拟及分析[J]. 武汉科技大学学报(自然科学版),2001,24(2):174-177. ZHANG Jian-hua, LI Shi-lu, WANG Yu-jie. Numerical simulation of springing blasting in stemmed hole[J]. Journal of Wuhan Uni. of Sci.&Tech.(Natural Science Edition), 2001,24(2):174-177. [11]杨善元. 岩石爆破动力学基础[M]. 北京:煤炭工业出版社,1993.

2 数值模拟参数
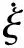

3 计算方案及模型
3.1 计算方案
3.2 计算模型

4 数值计算结果


5 结 论

