“碰撞与动量守恒”的层次及教学*
潘仕恒
(广州市白云中学 广东 广州 510168)
从宏观小球到微观粒子的碰撞,在满足一定的条件下,无不遵循动量守恒这一规律,作为自然界的基本守恒定律之一,动量守恒定律在物理学中具有很高的地位,在教育部考试中心颁布的《考试大纲》中标识为Ⅱ级内容[1],其重要性不言而喻.
然而,“碰撞与动量守恒”又是高中物理中最具难度的一章,具体表现在如下几方面:
一是研究对象复杂(两个以上),涉及物理量多;
二是物理过程复杂,物理情境抽象,问题的综合性强,与所有力学规律都可建立综合;
三是数学应用复杂,有多元(二次)方组的列举和运算,有数值解和字母解,部分还涉及矢量(向量)运算法则.
为了帮助学生克服本章学习困难,笔者根据多年的教学经验和认知规律,对全章的知识点和能力层次重新组织,建立由浅入深循序渐进的教学路线,下面与读者共享.
1 教学内容的层次分析
任何教学内容都有一定的层次,它与知识的地位及教学目标有关.课程标准[2]和《考试大纲》都对“碰撞与动量守恒”有清晰的层次规定.
课程的内容标准为:知道弹性碰撞和非弹性碰撞,理解动量和动量守恒定律,能用动量守恒定律分析一维碰撞;《考试大纲》把它们归纳为两个层次并标识要求掌握的程度:弹性碰撞和非弹性碰撞(Ⅰ),动量、动量守恒定律及其应用(Ⅱ).标识Ⅰ对应于课标 “了解”“知道”“认识”的知识和要求,为第一个层次.标识Ⅱ对应于课标 “理解”和“应用”的知识和要求,为第二个层次.
就教学而言,第一层次属基础层次的要求,教学难度不宜大.而第二层次则是更高层次的要求,相应的教学有一定的难度.同时,“理解”和“应用”仍然具有相对性,如“理解”可分为“初步理解”“一般理解”和“深入理解”,“应用”水平也有“简单应用”“综合应用”或“复杂应用”.
为了更好地区分、把握第二层次,有必要再把它细分为三个等级的要求[3]:
第一级为学生能够正确理解概念和规律的含义以及它们在简单情况下的应用,问题难度以“易”为主;
第二级为学生能理解概念和规律的确切含义和准确表达,能理解规律的适用条件,并正确运用规律解决相关的问题,教学难度以“中等”为主,是多数学生要达到的知识和能力目标;
第三级为学生对物理规律的逻辑性认知达到较高水平,对复杂、抽象物理过程和物理情境有较好的理解,综合能力、数学应用能力较强,对应的问题难度为“难”,是进一步拓展学生能力之必需[4].
当教学对象的知识起点不高时,可着重实施第一、第二级要求的教学;如果学生的起点较高,则可着重实施第二级要求的教学并向第三级扩展.
2 教学内容的层次划分
根据上述教学目标和教学层次分析,现将“碰撞与动量守恒”的知识点进行分层归类,并提出教学建议.
第一层次的教学内容有:知道冲量、动量的定义及特点,了解冲量和动量变化的关系(动量定理),能用动量守恒定律求解简单的碰撞问题(一维,无外力).在教学操作上,冲量、动量定理只要求定性了解,而动量和动量守恒定律则要求定量掌握:引导学生合理规定正方向,在一维碰撞中正确列出守恒方程并进行简单的计算,暂不做能力扩展,教学难度以“易”为主.由于概念多,新知识多,教学用时建议为3课时,给学生充分的新知识同化时间.
第二层次的教学是全章的重点和难点,要求学生正确理解动量的特点(与动能的区别等)和动量守恒的条件,理解三类碰撞中的内力和外力特点,正确应用动量守恒定律和能量关系求解相关碰撞问题.对于弹性碰撞,不仅要求学生能列出动量和动能守恒的方程组,并能对方程组的解进行讨论,掌握等质量小球的弹性碰撞特点.教学难度以“中等”为主,达到第二级要求即可.由于是全章的教学重心,教学用时建议为4课时.
考虑到知识的发展与学生能力拓展的需要,还应进行第三级的教学扩展,使学生能运用动量守恒定律并综合动能定理、机械能守恒定律、牛顿定律等高级规则解决力学问题,从而培养提高学生对物理过程和物理情境的分析能力、综合能力以及数学应用能力.这一层次的教学难度较大,技术上可引导学生把形形色色的力学综合题归类,寻找它们的共同特点,或者将大问题分解为若干个小问题,以降低学生接受知识的难度.
对于新课教学,通常达到第二级要求层次即可,第三级要求可在高三总复习中实现.当然,如果学生基础较好,可在第三级要求上做适当的扩展.
3 教学层次的范例列举
以下给出各层次教学的范例,不仅体现全章的教学层次,也反映全章的教学框架:从易到难,循序渐进.
3.1 第一层次问题范例
由于这一层次的教学重点是基本概念和基本规律的教学,要控制难度,既要使学生容易获得新知识,又有利于后续学习能力的形成和学习信心的提高.
【例1】质量为m=1kg的3个小球分别做匀速直线运动、圆周运动和平抛运动,某时刻的速度大小均为2m/s,分析此刻各自的动量特点.
本例题要求定量理解动量的大小、单位和方向,体现概念的初步学习,难度不大.
【例2】如图1所示,光滑的水平面上有两个小球同向运动.A的质量为1kg,速度为10m/s;B的质量为4kg,速度为1m/s.发生碰撞之后立即分开,B的速度变为4m/s,求碰撞后
(1)A 的速度;
(2)碰撞过程损失的动能是多少?
答案:-2m/s;18J.
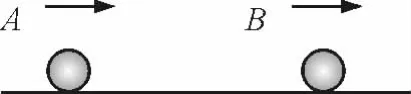
图1
本例题为动量守恒定律的初步应用,仅限于光滑水平面上的一维碰撞,不拘泥细节,不引入碰撞的条件,要求学生正确规定正方向,正确表达动量守恒定律.教学中亦可引入“一动一静”“反向碰撞”“反弹”等模型,可以求碰撞前、后的速度和动量,可扩展到求解动能(能量)的损失量.通过多角度的应用,使学生对“运用动量守恒定律解决碰撞问题”形成初步的认识.
3.2 第二层次问题范例
本层次的教学要求学生正确理解动量和动量守恒的条件,理解三种碰撞的特点并能运用守恒定律处理常见问题.
以下例题涉及非弹性碰撞、完全非弹性碰撞和弹性碰撞,能较好地帮助学生深入理解动量守恒的条件、特点和应用方法,难度中等,教学要求达到第二级.
【例3】A和B两小球在水平面上沿同一方向运动,两球的动量分别为pA=6kg·m/s,pB=10kg·m/s.当A球追及B球发生对心碰撞后,关于两球动量pA′和pB′,正确的是(规定原来方向为正)
A.pA′=7kg·m/s,pB′=9kg·m/s
B.pA′=6kg·m/s,pB′=10kg·m/s
C.pA′=-6kg·m/s,pB′=22kg·m/s
D.pA′=-3kg·m/s,pB′=19kg·m/s
答案:D.
【例4】如图2所示,在水平光滑直导轨上,静止着3个质量均为m=1kg的相同小球A,B,C,现让A 球以v0=2m/s的速度向着B球运动,A和B两球碰撞后黏合在一起,两球继续向右运动并跟C球碰撞,C球的最终速度vC=1m/s.
(1)A和B两球跟C球相碰前的共同速度为多大?
(2)A和B两球最终的速度是多大?
(3)两次碰撞过程中一共损失了多少动能?
答案:(1)v=1m/s;(2)vAB=0.5m/s;
(3)ΔEk=1.25J.
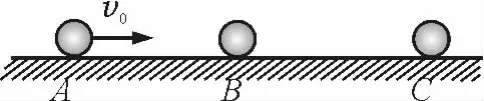
图2
【例5】在水平光滑直导轨上,质量为m=1kg的小球A以v0=2m/s的速度向静止的B球运动,B球的质量为M=3kg.A和B两球发生弹性碰撞后,各自的速度是多少?
答案:以小球A 的初速度为正,-1m/s,1 m/s.
在做上述例题分析时,可引入存在外力(摩擦力)的情形,但当内力远大于外力时(碰撞时间很短),动量守恒依然成立.由于本层次教学是全章的教学重点,故仍然有一定的难度.
3.3 第二层次的第三级要求范例
这是本章最具挑战的教学层级,涵盖了《考试大纲》要求考查的除了实验能力以外的其他4种能力:理解能力、推理能力、分析综合能力和应用数学处理物理问题的能力.虽然难度大,但有一定的规律可寻.下列三类问题是大多数综合题的母题或原题,由它们可变式出丰富多彩的力学综合题,故在教学中要讲透.
3.3.1 与机械能(或动力学规律)的综合
【例6】如图3,一光滑水平桌面AB与一半径为R的光滑半圆形轨道相切于C点,且两者固定不动.一长L为0.8m的细绳,一端固定于O点,另一端系一个质量m1为0.2kg的球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.8kg的小铁球正碰,碰后m1小球以2m/s的速度弹回,m2将沿半圆形轨道运动,恰好能通过最高点D.g=10 m/s2,问:
(1)m2在圆形轨道最低点C的速度为多大?
(2)光滑圆形轨道半径R应为多大?
答案:(1)1.5m/s;(2)0.045m.
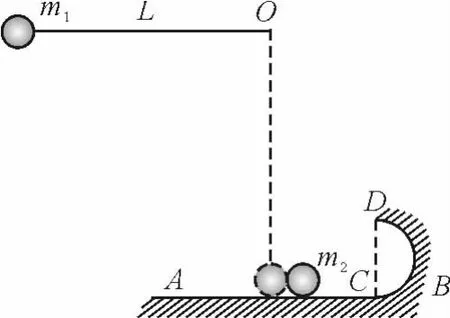
图3
3.3.2 子弹打木块模型
子弹打木块模型是动量守恒定律教学中绕不开的问题,几乎一半的力学综合题是从该模型中演化出来.
【例7】如图4所示,设质量为m=0.2kg的子弹以初速度v0=200m/s射向静止在光滑水平面上的质量为M=1.8kg的木块,并留在木块中不再射出,子弹钻入木块深度为d=0.2m.求
(1)木块对子弹的平均阻力的大小和该过程中木块前进的距离;
(2)系统损失的动能.
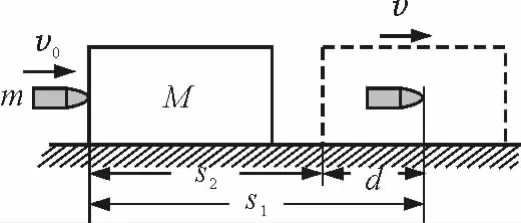
图4
答案:(1)1.8×104N,0.02m;(2)3.6×103J.
本题要求学生不仅会列出动量守恒定律方程,还要熟练地对子弹、木块和系统列出相应的动能定理方程.下面两个重要结论,要求学生掌握:
结论1:阻力(摩擦力)产生的热能:Q=fd;
结论2:系统损失的动能转化为热能(能量守恒),即
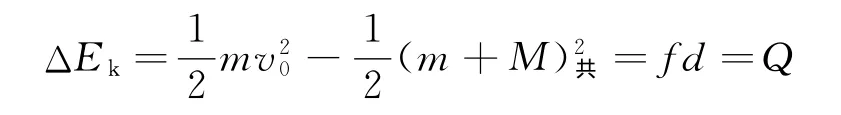
结论中,d为子弹相对木块的距离,若子弹穿出,结论仍成立,只是子弹和木块的末速度不相等.本模型可扩展为小物块在大木块(或小车)上的相对运动问题,如图5所示.

图5
3.3.3 碰撞中的弹簧问题
弹簧模型本质上就是弹性碰撞模型,是第二大类的力学综合题型.要求学生弄清弹簧处在压缩量最大和原长两个特殊位置的动量和能量特点,其他问题将迎刃而解.
【例8】如图6所示,用轻弹簧相连的质量均为2 kg的A和B两物块都以v=6m/s的速度在光滑水平地面上运动,弹簧处于原长,质量4kg的物块C静止在前方,B与C碰撞后二者粘在一起运动.在以后的运动中,问:
(1)当弹簧的弹性势能最大时,物体A的速度多大?
(2)弹性势能的最大值是多大?
(3)A的速度有可能向左吗?为什么?
图6
答案:(1)3m/s;(2)Ep=12J;(3)不可能.
还有难度更大的多次碰撞问题,可根据学生的能力层次继续扩展,限于篇幅,不再列举.
4 结束语
笔者所在的学校为非重点中学,学生层次中等偏下,教学难度较大.但通过分层推进,较好地实现了课程目标:普通班的教学能推进到第二级要求,重点班则能推进到第三级要求.在以上述例题为尺度的考试评价中,重点班、普通班均取得较好的成绩.因此,分层推进是应对高难度内容的有效方法,它使各层次的学生学有所获,而不是望而止步.
类似“碰撞与动量守恒”内容,涉及的问题太复杂,教学过程决不可以照本宣科,而是要根据教学目标和学生实际进行二次创作.笔者的尝试是提供一种思路或方法,期待起到抛砖引玉的作用.
1 教育部考试中心主编.2013年普通高等学校招生全国统一考试大纲.北京:高等教育出版社,2013
2 教育部.普通高中物理课程标准(实验).北京:人民教育出版社,2003
3 潘仕恒.高中物理课程分级评价浅探.中学物理教学参考,2012(1,2)
4 廖伯琴,张大昌编.普通高中物理课程标准(实验)解读.武汉:湖北教育出版社,2004
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论

