刚体转动惯量的求解讨论

赵 强 韩春杰

（石家庄机械化步兵学院 河北 石家庄 050083）

刚体转动惯量是描述刚体转动特性的重要物理量之一，其大小不仅与刚体的总质量有关，而且还和质量相对于轴的分布有关，同一刚体对于不同的转轴，转动惯量不同.教学过程中我们发现，学员在求解刚体转动惯量常常不得要领.本文总结了求解刚体转动惯量的方法.

1 定义求解法

刚体对转轴的转动惯量等于组成刚体的各质点的质量与各质点到转轴的距离平方的乘积之和，定义式为J＝，对于质量连续分布的刚体，则可用积分代替求和，即.此式仅可用于求解几何形状简单、质量连续且均匀分布刚体的转动惯量.

【例1】求均匀细棒绕垂直通过质心转轴的转动惯量.

分析：这类问题求解的关键是如何取质元dm使问题简化.当刚体质量为线分布时，取dm＝λdl；当质量为面分布时，则取dm＝σdS；当质量为体分布时，则取dm＝ρdV.式中λ，σ和ρ分别为线质量密度、面质量密度和体质量密度，dl，dS和dV分别为所取的线元、面元和体元.由此可见，本题可在沿棒的方向取质量线元dm即可方便求解.

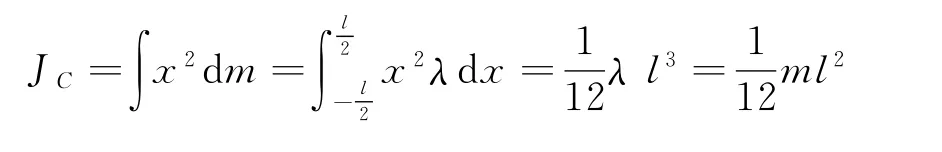
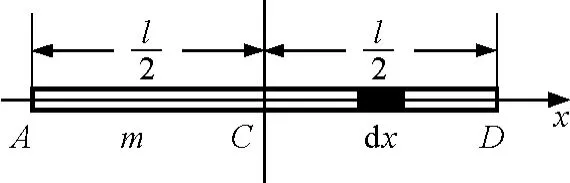
图1

2 定理求解法

2.1 利用平行轴定理求解

当质量为m的刚体绕通过质心转轴的转动惯量JC已知，若另一轴与此轴平行且相距为d，则此刚体对后一轴的转动惯量可表示为

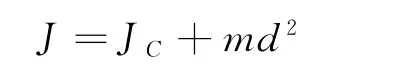
上式即为平行轴定理.

【例2】计算例1中细棒绕端点D的转动惯量.

分析：对于过端点D的转动惯量，可根据平行轴定理来计算，此时

解：根据平行轴定理JD＝JC＋md2，以及绕质心轴的转动惯量，可得

2.2 利用垂直轴定理求解

设刚体厚度为无穷小的薄板平面xy，z轴与之垂直（如图2所示），则对于任何原点O绕3个坐标轴的转动惯量分别为

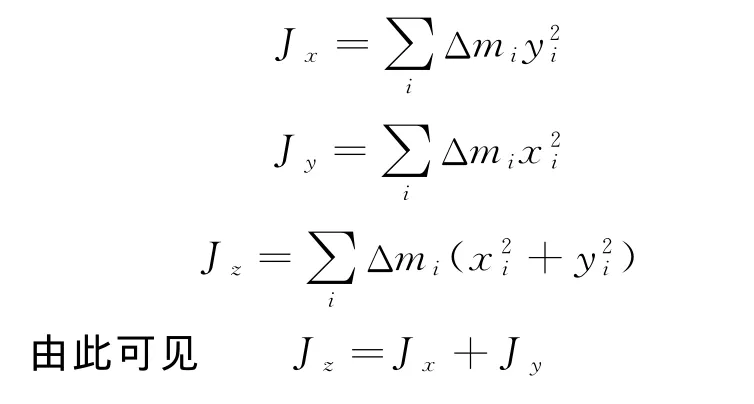
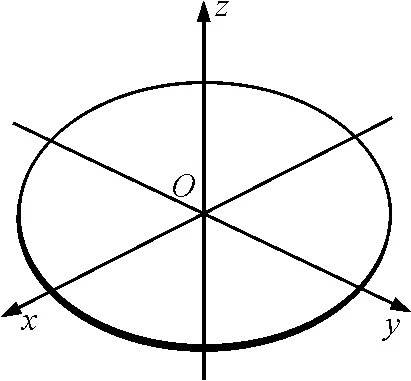
图2

显然，无穷小厚度的薄板对与它垂直的坐标轴的转动惯量，等于薄板对板面内另外两个直角坐标轴的转动惯量之和，即垂直轴定理.

【例3】均质等厚度薄圆板的质量为m，半径为R，板的厚度远小于半径.求对过圆心且在板面内之轴的转动惯量.

分析：由题设条件可知，板的厚度远小于半径，所以，此圆板可看作无穷小厚度的板.可利用垂直轴定理求解.

解：以盘心为原点O，x和y轴在板面内.根据对称性可知Jx＝Jy，由垂直轴定理，得

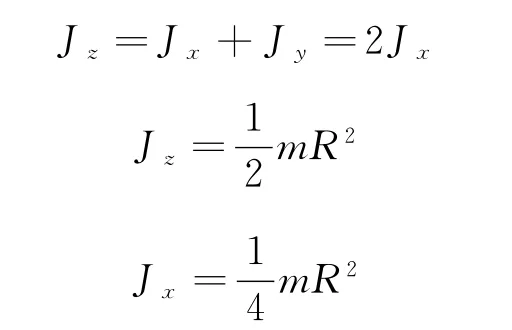
2.3 利用转动惯量定理求解

在求解转动惯量时，我们还经常用到转动惯量定理

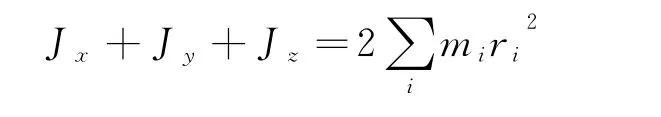
其中Jx，Jy，Jz表示绕3个互相垂直相交轴的转动惯量，mi为第i个质点的质量，ri为第i个质点离开3轴交点的距离，当刚体质量连续分布时，定理可表述为，这样，可以把对3轴线的积分转化成对坐标原点的积分，从而大大降低了积分的难度.

【例4】求质量为M，半径为R实心球绕直径轴的转动惯量.

分析：由于实心球绕任何直径轴的转动惯量都相等，以球心为坐标原点，则有

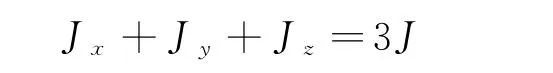
通过转动惯量理即可求得.实心球体绕直径的转动惯量.

解：由转动惯量定理和实心球体的对称性可得

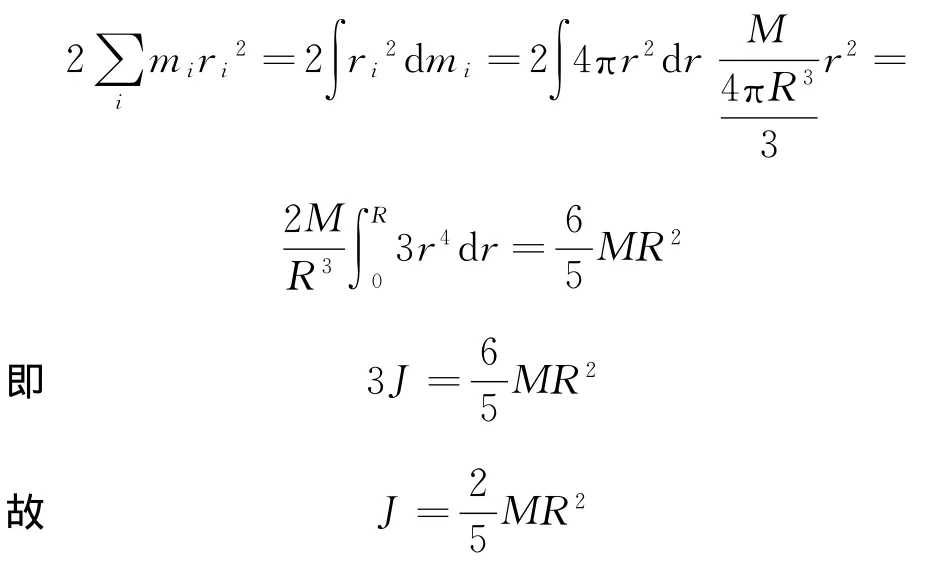
3 质量投影法

由转动惯量的定义我们不难发现，如果刚体上各质元mi到转轴距离ri保持不变，那么刚体对此转轴的转动惯量不变.依据这一结论，在保持总质量不变的前提下，如果把三维刚体上各质元的质量向垂直于转轴的平面“投影”，便可将三维刚体简化为二维刚体，通过这一变换得到的刚体平面对转轴的转动惯量与三维刚体对同一转轴的转动惯量相等.以此类推，对于二维刚体可将刚体平面的质量“投影”到该平面上某轴进而简化为一维刚线，由此计算出的转动惯量与刚体平面对同一转轴的转动惯量相等.

利用质量投影法可以较方便求得椭圆盘、六面体、圆柱体、圆台体等均质刚体对转轴的转动惯量.

【例5】如图3所示，质量m的均质薄椭圆盘，其长、短半轴长为a和b，分别计算其对x，y，z轴的转动惯量.

分析：利用质量投影法，将椭圆盘分别向x，y轴投影求出y，x轴的转动惯量，然后再根据垂直定理求出椭圆盘对z轴的转动惯量.

图3

解：首先求椭圆盘对x轴的转动惯量.此时，可将椭圆盘向y轴投影得到长为2 b的线段，质量仍为m，注意这时的质量非均匀分布，可求得质量线密度为

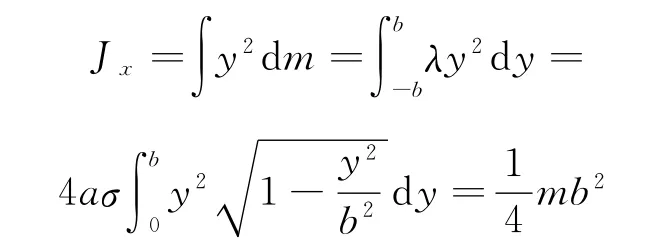
同理可得均质椭圆盘对y轴的转动惯量

4 标度变换法求解

若物体的质量为m，通过物体质心C的轴的方向用i表示.该物体对i轴的转动惯量可表示为J＝kml2，其中k是常量，由物体的形状和i的方向决定，l是物体的特征尺寸.

如果能够把物体分成n等分，其形状和取向都和原物体一样，每个小块对质心的转动惯量都可以用上式表示，且常量k相同，但m和l的值却不同，那么物体的转动惯量可用下式求得

其中Ji为第i个小块对通过质心C的轴的转动惯量.

【例6】求均匀立方体绕通过面心的中心轴的转动惯量.

分析：如图4所示，将此立方体分成8个相等的小立方体，求出一个小立方体对棱边转轴的转动惯量，然后，根据转动惯量的可加性求出整个立方体对过面心的中心轴的转动惯量.

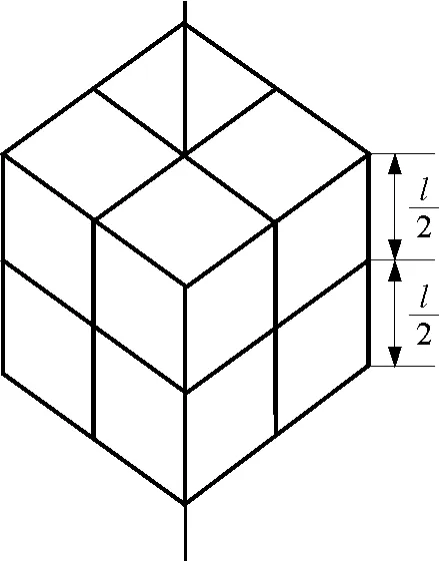
图4

解：设立方体的质量为m，棱长为l，JC＝kml2，中心轴到棱边的距离为，由平行轴定理可知，立方体绕棱边的转动惯量为

8个小立方体绕棱边的转动惯量之和应等于大立方体绕中心轴的转动惯量

1 漆安慎，杜婵英.普通物理学教程.北京：高等教育出版社，2005

2 祝之光.物理学上册（第二版）.北京：高等教育出版社，2004

3 John.F.Streib.关于转动惯量定理.大学物理，1992，11（2）

4 王永超.刚体转动惯量的质量投影法.大学物理，2010（9）