关注图像的物理意义

薛庆勉

（中央民族大学附属中学 北京 100081）

对于物理问题，我们可以通过图像来直观地分析两个物理量的关系，尤其是当运动过程分为多阶段时，图像往往能清晰地反映出整个运动过程的特点，比计算法更简洁明了.在中学阶段我们最常关注的是图像的斜率和“面积”，例如：v－t图像中斜率可以表示加速度a，而v－t图像中“面积”可以表示位移s；在F－t图像中，“面积”表示F的冲量，在φ－x 图像中，斜率表示场强E等等，但是在应用图像时应关注图像的物理意义，并不是所有图像的斜率和“面积”都有自身的物理意义.

【例1】如图1所示，四分之一光滑绝缘圆弧轨道AP和水平绝缘传送带PC固定在同一竖直平面内，圆弧轨道的圆心为O，半径为R.传送带PC之间的距离为L，沿逆时针方向的传动速度在PO的右侧空间存在方向竖直向下的匀强电场.一质量为m，电荷量为＋q的小物体从圆弧顶点A由静止开始沿轨道下滑，恰好运动到C端后返回.物体与传送带间的动摩擦因数为μ，不计物体经过轨道与传送带连接处P时的机械能损失，重力加速度为g.（前两问略）

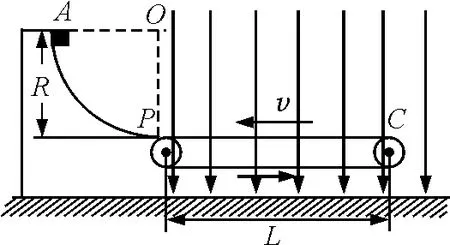
图1

（3）若在PO的右侧空间再加上方向垂直于纸面向里、磁感应强度为B的水平匀强磁场（图中未画出），物体从圆弧顶点A静止释放，运动到C端时的速度为试求物体在传送带上运动的时间t.

解：该题的标准解答如下.

（1）设电场强度为E，在无磁场时物体从A端运动到C端的过程中，根据动能定理，有

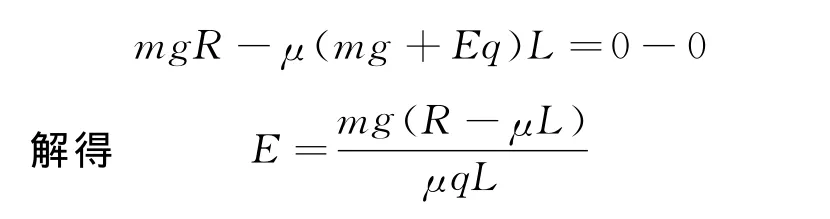
在有磁场情况下物体从P端运动到C端的过程中，设任意时刻物体速度为v，取一段极短的含此时刻的时间Δt，设在此时间段内的速度改变量为Δv（取水平向右为正方向），根据牛顿第二定律，有

两边同时乘以Δt，再对两边求和，有

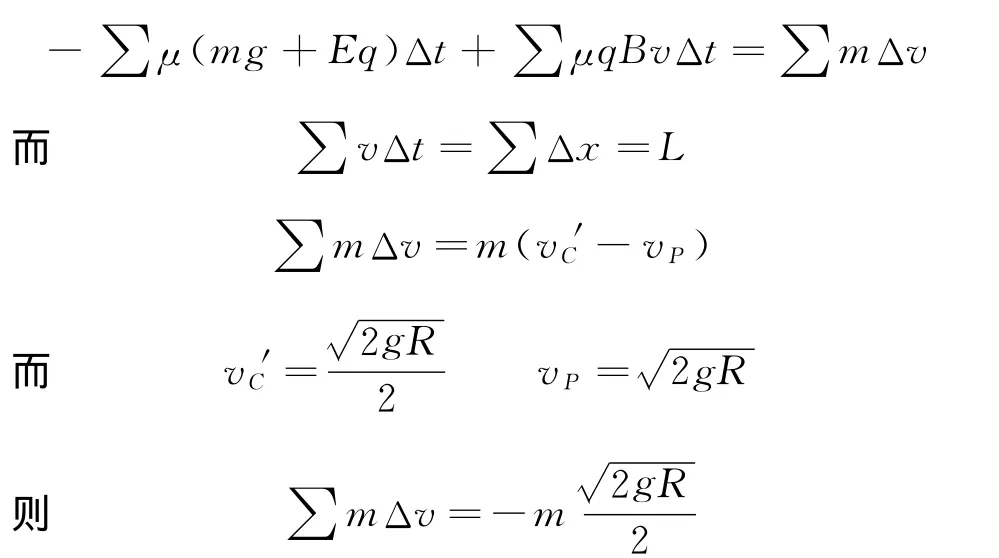
以上结果代入上式，得

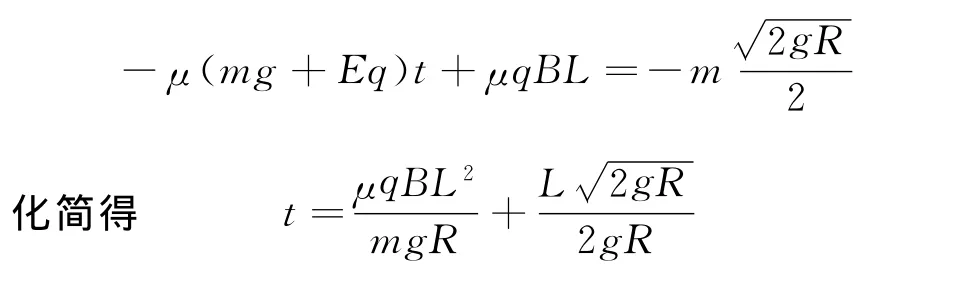
在试卷讲评中，有同学用以下方法求解，过程如下.

（2）物体从P端运动到C端的过程中，所受摩擦力为变力，设任意时刻物体速度为v，则

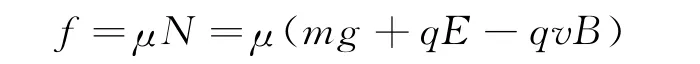
又因为

可以看出f和v是线性关系，画出f－v的图像如图2所示.

图2

图中v0表示物体在P点的速度

根据P＝Fv，所以认为f－v图中阴影部分面积表示该段时间内的平均功率，再根据动能定理可得

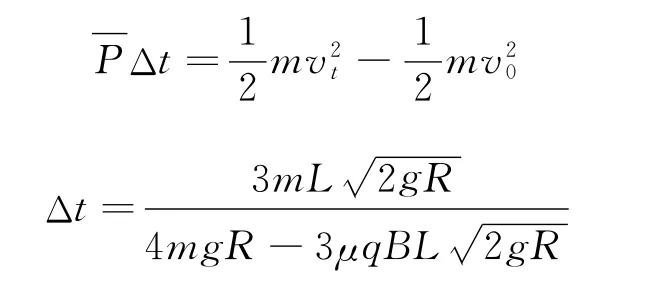
很明显用以上两种方法的到的答案是完全不同的，问题出在哪里？经过仔细分析我们可以看出：问题就出在f－v图像的“面积”上.f－v图像中，其“面积”并不能代表平均功率，因为它的面积没有任何物理意义.为什么在有些物理问题中可以用面积求解，例如：因为s＝vt，在v－t图像中就可以用“面积”求位移；因为W＝Fs，所以在F－s图像中就可以用“面积”求力所做的功；因为U＝Ed，所以就可以在E－d图像中用“面积”求两点间的电势差……那么同样满足式子P＝Fv，为什么F－v图像的面积就没有任何意义呢？原因在于位移s，功W，电势差U其实都是一个累积量，当我们把时间取的无限小的时候，位移是速度对时间的积分，s＝vΔt；把位移取的无限小的时候，功是力对位移的积分，W ＝FΔs；电势差是电场强度对位移的积分，U＝EΔd……而功率不是一个累积量，它并不是力对速度的积分，从定义上说，而不是＝FΔv，所以不能一味根据公式就判定其图像中的“面积”一定具有某种物理意义，例如最简单的匀变速直线运动中，由于F是恒力，所以F－v的图像如图3所示.

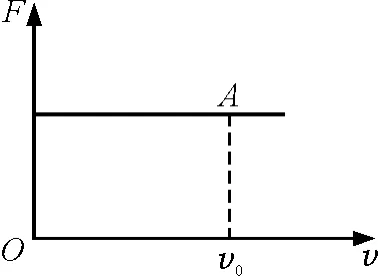
图3

如果考虑速度从零加速到v0阶段，而不是Fv图像中围成的“面－积”Fv0.

所以在F－v图像中我们只能用某点的横纵坐标的乘积求该位置（或该时刻）的瞬时功率，而不能根据“面积”求该过程中中的平均功率.

另外一种情况就是U－I图，在U－I图中，如图4所示.我们也只能用某点的横纵坐标的乘积求该位置（或该时刻）的瞬时功率，而不能根据“面积”求该过程中的平均功率.因为虽然满足P＝UI，但是P并不是UI的累积量，不能进行叠加求和.

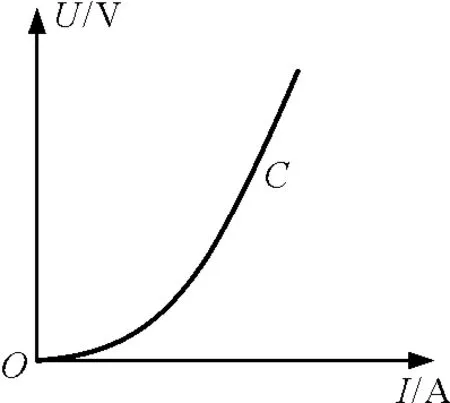
图4

同理在U－I图像中，如果我们要求某点C的电阻，只能用该点的纵坐标（电压）除以该点的横坐标（电流）进行计算，而不能用C点的斜率来计算该点的电阻，因为电压U并不是电流对电阻的积分叠加，所以不能用斜率表示电阻大小.

由此可见，并不是所有图像的斜率和“面积”都有其特定的物理意义，在应用图像解决问题时不能仅仅考虑物理量之间的数学关系，还要考虑到图像自身的物理意义.