不可逆矩阵的伴随矩阵的特征值与特征向量的求法

王莲花， 王 萍(.北京物资学院 信息学院，北京 通州049； .孔集乡第一中学 数学组，河南 宁陵 4767)

不可逆矩阵的伴随矩阵的特征值与特征向量的求法

王莲花1， 王 萍2

(1.北京物资学院 信息学院，北京 通州101149； 2.孔集乡第一中学 数学组，河南 宁陵 476712)

给出矩阵A不可逆时，其伴随矩阵A*的特征值和特征向量的简便求法，即当r(A*)=0时，A*的所有的特征值都为零，任一非零向量都是其特征向量；当r(A*)=1时，A*有n-1个特征值为0，另一个特征值为A11+A22+…+Ann，此时，若A11+A22+…+Ann=0，则A*的属于特征值为0的所有特征向量由A的n-1个线性无关的列向量生成；若A11+A22+…+Ann≠0，A*的属于特征值为0的所有特征向量由A的n-1个线性无关的列向量生成，属于A11+A22+…+Ann的特征向量由A*的行元素的比例系数组成.

不可逆矩阵；伴随矩阵；特征值；特征向量

0 引言

我们知道，如果n阶可逆矩阵A的特征值为λ1,λ2,…,λn，相应的特征向量分别为α1,α2,…,αn，则伴随矩阵A*的特征值为μi=|A|/λi(i=1,2,…,n)，相应的特征向量也分别为α1,α2,…,αn，即A*αi=μiαi(i=1,2,…,n).那么，如果矩阵A不可逆，其伴随矩阵A*的特征值和特征向量除常规求法外，有没有其他简便快捷的方法呢？本文从理论上给出当A不可逆时，不需要解线性方程组，只需要利用矩阵A本身并通过简单的计算，就能很快写出A*的特征值和特征向量的方法.

1 相关引理

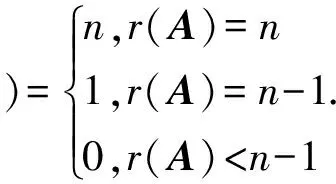
引理2[1]设矩阵A=(aij)n×n的特征值为λ1,λ2,…,λn，则λ1+λ2+…+λn=a11+a22+…+ann.

引理3设A是n阶矩阵，A*是A的伴随矩阵，Aij为A中元素aij对应的代数余子式. 若μ1,μ2,…,μn是A*的特征值，则μ1+μ2+…+μn=A11+A22+…+Ann.

引理3显然可以直接由引理2得出.

2 主要结论

定理设A是n阶不可逆矩阵，A*是A的伴随矩阵，Aij为A中元素aij对应的代数余子式，记μ1,μ2,…,μn是A*的特征值，则

(1)若r(A*)=0，则μ1=μ2=…=μn=0，此时，任一非零列向量均为A*的特征向量.

(2)若r(A*)=1，则μ1=μ2=…=μn-1=0，μn=A11+A22+…+Ann[2].

1) 若A11+A22+…+Ann=0，则A*的特征向量由A的n-1线性无关的列向量生成；

2)若A11+A22+…+Ann≠0，则A*的属于特征值0的特征向量由A的n-1个线性无关的列向量生成；如果A11,A21,…,An1不全为零，则属于μn的线性无关的特征向量为αn=(1,b2,…,bn)Τ，其中1,b2,…,bn为实数.

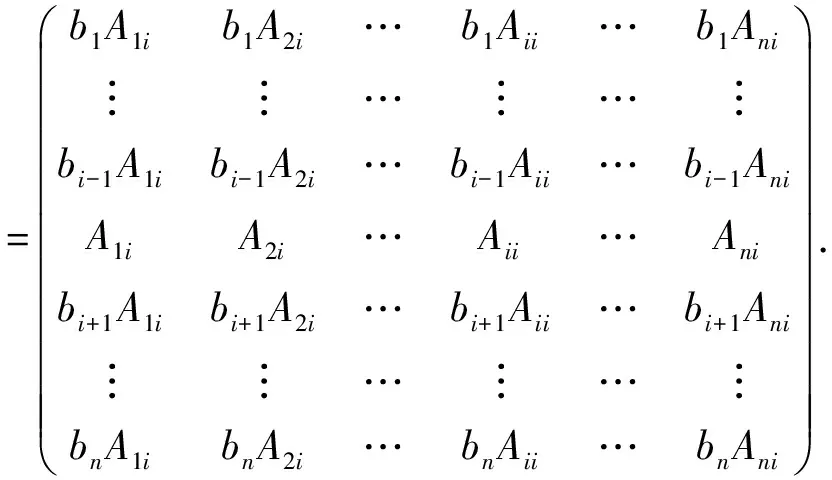
一般地，若A1i,A2i,…,Ani不全为零，则属于μn的线性无关的特征向量为αn=(b1,…,bi-1,1,bi+1,…,bn)Τ，其中bi(i=1,…,i-1,i+1,…,n)为实数.

证明当A不可逆时，由引理1知，r(A*)≤1.

(1)若r(A*)=0，则A*=0，则μ1=μ2=…=μn=0，显然，任一非零列向量均为A*的特征向量.

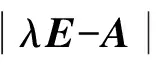
1)若A11+A22+…+Ann=0，此时，A*的特征值全为零，而由A*A=0，因r(A)=n-1，故A的列向量组的秩为n-1，而A的n-1个线性无关的列向量组为A*的特征向量，对应的特征值为0. 由A*X=0的解空间为n-1维的，因而A*的特征向量由A的n-1线性无关的列向量生成.

2)若A11+A22+…+Ann≠0，这时，A*有n-1个特征值为0，另一个特征值是μn=A11+A22+…+Ann≠0. 由A*A=0，则A中有n-1个线性无关的列向量均为A*的属于特征值0的特征向量.下求A*的对应于特征值μn=A11+A22+…+Ann的特征向量.

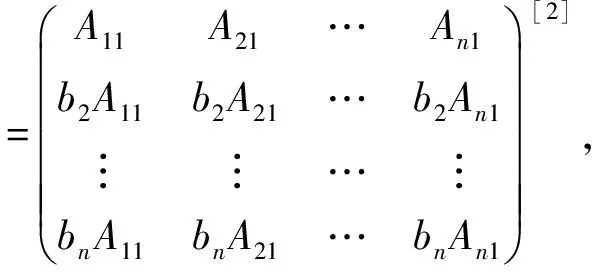
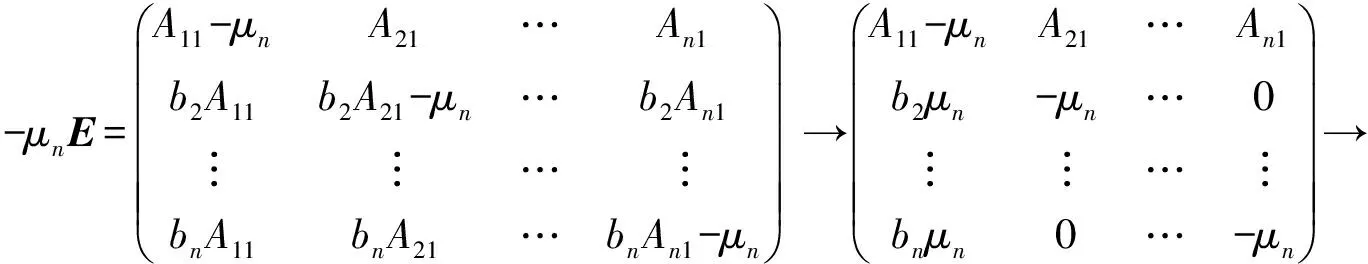
对应的同解线性方程组为

注意：由μn=A11+A22+…+Ann=A11+b2A21+…+bnAn1，得一个基础解系，即属于μn的线性无关的特征向量为αn=(1,b2,…,bn)Τ.

类似可证：A1i,A2i,…,Ani不全为零时，属于μn=A11+A22+…+Ann的线性无关的特征向量为αn=(b1,b2,…,bi-1,1,bi+1,…,bn)Τ. 只不过，在证明过程中设A*如下即可.

3 应用举例

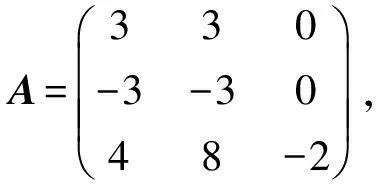
解因为r(A)=2，所以r(A*)=1，A*中每行元素对应成比例，且A中元素a11=3,a22=-3,a33=-2的代数余子式分别为A11=6,A22=-6,A33=0，因此A*的特征值为λ1=λ2=0,λ3=A11+A22+A33=6-6+0=0，由定理知，A的两个线性无关的列向量α1=(3,-3,4)Τ,α2=(0,0,-2)Τ是属于λ1=λ2=λ3=0的线性无关的特征向量.

因此A*的属于λ1=λ2=λ3=0的特征向量为k1α1+k2α2(k1,k2为任意常数).

解因为r(A)=2，所以r(A*)=1，A*中每行元素对应成比例，且A中元素a11=1,a22=-5,a33=1的代数余子式分别为A11=4,A22=-3,A33=1，因此A*的特征值为λ1=λ2=0,λ3=A11+A22+A33=4-3+1=2，由定理知，A的两个线性无关的列向量α1=(1,-2,2)Τ,α2=(3,-5,3)Τ是属于λ1=λ2=0的线性无关的特征向量.

又由r(A*)=1知，A*的矩阵的3行是成比例的，由A11=4,A21=3,A31=1和A11=4,A22=-3,A33=1知，b2=-1,b3=1，因此，属于λ3=2的线性无关的特征向量为α3=(1,-1,1)Τ.

因此A*的属于λ1=λ2=0的特征向量为k1α1+k2α2(k1,k2为任意常数)；属于λ3=2的特征向量为kα3(k为不等于零的任意常数).

[1]北京大学数学系几何与代数教研室前代数小组. 高等代数[M]．王萼芳，石生明，修订．北京：高等教育出版社，2003．

[2]王品超. 高等代数新方法[M].徐州：中国矿业大学出版社，2003.

TheMethodofEigenvaluesandEigenvectorsaboutAdjoin
MatrixofIrreversibleMatrix

WANG Lian-hua1, WANG Pin2
(1.CollegeofInformation,BeijingWuziUniversity,Beijing101149,China;
2.MathematicsGroup,FirstMiddleSchoolofKongjiTownship,Ningling476712,China)

The simple and convenient method of eigenvalues and eigenvectors about adjoint matrix of irreversible matrix is given when the matrixAis irreversible matrix. That is, ifr(A*)=0, then all the eigenvalues ofA*is zero. Ifr(A*)=1,n-1 eigenvalues ofA*are zero, and another eigenvalue isA11+A22+…+Ann. At this time, ifA11+A22+…+Ann=0, all the eigenvectors ofA*belonging to zero eigenvalue are generated fromn-1 linearly independent columnA. IfA11+A22+…+Ann≠0, the eigenvectors ofA*belonging to zero eigenvalue are generated ofn-1 linearly independent columnA, and the linearly independent eigenvectors ofA*belonging toA11+A22+…+Annare composed by matrixAline element proportionality coefficient.

irreversible matrix; adjoint matrix; eigenvalue; eigenvector

2013-08-14

北京物资学院专业建设——信息类专业群建设(PXM2012_014214_000022)

王莲花(1964—)，女，河南宁陵人，北京物资学院信息学院副教授，主要研究方向：代数及其应用.

10.3969/j.issn.1007-0834.2014.01.001

O172.2

A

1007-0834(2014)01-0001-03