函数在点x=x0处可导的充分条件

郭欣红(辽宁金融职业学院 素质教育学院， 辽宁 沈阳 110122)

函数在点x=x0处可导的充分条件

郭欣红

(辽宁金融职业学院 素质教育学院， 辽宁 沈阳 110122)

通过几个例子指出判断函数在一点处是否可导要注意它的充分条件，剖析了错误判断产生的原因.

函数；可导；充分条件

导数是微积分中的一个基本概念，关于函数f(x)在点x=x0处是否可导，一般是根据导数定义和定理，即函数y=f(x)在x=x0点可导的充要条件是：左右导数存在且相等.如果对导数概念没有深刻领会和理解，往往会对一些相关结论做出错误判断.本文列举了几个例子，剖析判断函数在x=x0处是否可导应注意它的充分条件.

1 函数y=f(x)在点x=x0处是否可导

例1设函数f(x)在x=a的某个邻域内有定义，则f(x)在x=a处可导的一个充分条件是( )[1].

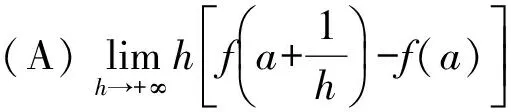
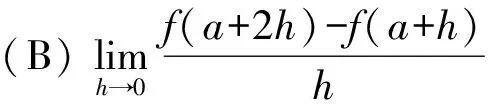
这道题很容易选错，如果对导数概念没有充分理解，会认为4个选项都对，而正确答案是(D)，下面我们来剖析一下其他3个选项错在哪儿.

1)剖析选项(A)： 如果函数在点x=a可导，根据导数定义，显然

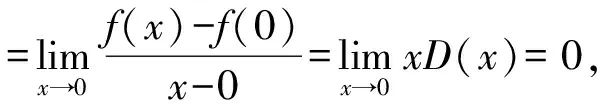
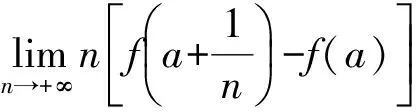
可见选项(A)是函数可导的必要不充分条件.

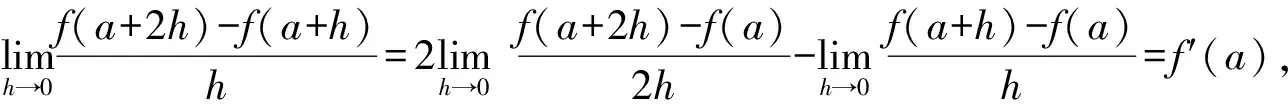
2 函数F(x)=f(x)+g(x)在x=x0处是否可导

例2函数f(x)和g(x)在点x0处可导是F(x)=f(x)+g(x)在该点处可导的( )[2].

(A) 充分不必要条件； (B) 必要不充分条件 ；(C) 充分必要条件 ；(D) 既不充分也不必要条件.

剖析此题容易错误地认为f(x)和g(x)在点x0处可导⟺F(x)=f(x)+g(x)在x0点可导，从而选(C).

例3函数f(x)和g(x)在点x0处可导是F(x)=f(x)·g(x)在该点处可导的( ).

(A)充分不必要条件；(B)必要不充分条件；(C)充分必要条件；(D)既不充分也不必要条件.

剖析同理此题也容易错误地认为f(x)和g(x)在点x0处可导⟺F(x)=f(x)·g(x)在x0点可导，从而选(C).

解如果f(x)和g(x)在点x0处可导，由导数定义可知，F(x)=f(x)·g(x)在x0处也可导；反之，则不一定成立.如f(x)=|x|，g(x)=-|x|，F(x)=f(x)·g(x)=-x2在点x=0处有导数，且F′(0)=-2x|x=0=0，然而f(x)=|x|，g(x)=-|x|,它们在点x=0处都不可导，因此选择(A)充分不必要条件.

3 函数在点x=x0处是否可导

剖析此题可以利用导数定义，分别求出左右导数，判断它们是否相等，也可以利用导数极限定理解决.

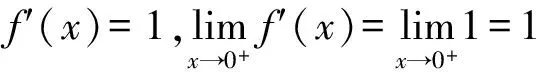
需要注意的是：导数极限定理只是函数在一点处可导的充分条件，如果把定理当做充要条件，很容易导致错误结果.

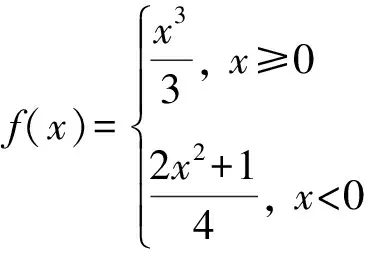
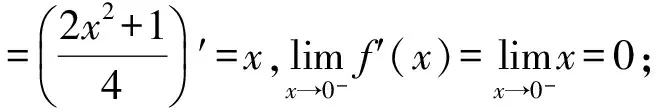
通过文中例题的剖析，我们看到，关注导数存在的充分条件，能更深入准确掌握导数的定义，加深对概念的理解.

[1]同济大学数学系.高等数学[M]. 6版.北京: 高等教育出版社, 2009：125

[2]吉米多维奇.数学分析习题集题解 [M]. 济南：山东科学技术出版社, 2005.

[3]时文俊. 分段函数分段点处可导性的讨论 [J]. 科技创新导报，2013(15)：168-169.

TheSufficientConditionfortheDerivableFunctionatthePointx=x0

GUO Xin-hong

(CollegeofQualityEducation,LiaoningFinanceVocationalCollege，Shenyang110122，China)

By several examples, it points out that sufficient condition should be paid attention to in judgment of whether the function is derivative and the reason of making error judgment is analyzed.

function; derivable; sufficient condition

2014-01-22

郭欣红(1969—)，女，辽宁沈阳人，辽宁金融职业学院素质教育学院教授，主要研究方向： 高等数学教学教法.

10.3969/j.issn.1007-0834.2014.01.002

O172.1

A

1007-0834(2014)01-0004-03