高一学生常见思维障碍的成因及对策
(江苏省青山高级中学,江苏 无锡 214000)
学好物理确实不容易,需要较强的能力,尤其是思维能力,它是学生顺利完成学习任务的关键和保障.从信息论的角度来看,思维是人脑对信息的加工过程.学生平时已经从日常生活经验和书本杂志以及互联网上获取了大量的信息,但是这些信息对物理问题的思考并不都有效,需要教师去引导、启发、归纳、分析和过滤,然后经过学生思维加工内化为学生掌握的知识和技能.高一学生常常因为思维定式和生活经验的误导,出现了一些思维障碍,造成学习物理的困难.
1 思维障碍的成因
1.1 生活负迁移
学生不自觉地绕过科学概念,从个人的日常经验和观念出发,想当然地对物理问题进行判断,得到错误结论.
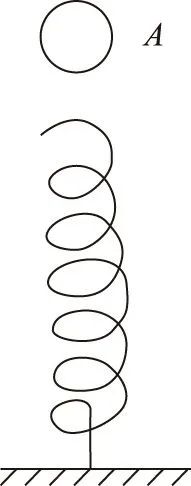
图1
例1 如图1所示,一个轻质弹簧竖直放在水平地面上,小球A由弹簧正上方某高度自由下落,与弹簧接触后,开始压缩弹簧,设此过程中弹簧始终服从胡克定律,那么在小球压缩弹簧的过程中,以下说法中正确的是( ).
A.小球速度一直增大
B.小球速度一直减小
C.小球速度先增大后减小
D.小球速度先减小后增大
在学生的答案中,第一次选择B的占70%以上,理由是“人运动中遇到障碍就会自我保护而减速,因此运动物体遇到弹簧弹力的阻碍也应该减速”.正确答案是C.
例2 甲、乙两队举行拔河比赛,甲队获胜,如果甲队对绳的拉力为F甲,地面对甲队的摩擦力为f甲;乙队对绳的拉力为F乙,地面对乙队的摩擦力为f乙,绳的质量不计,则有F甲F乙,f甲f乙.(答案:=、>)
在学生的答案中,第一空填“=”的占80%左右,而第二空填“>”的不足10%,理由 是“只有F甲>F乙时,受力不平衡了,运动状态改变,导致向甲队方向移动,最后甲队获胜”.
例3 物体A、B同时从同一地点、沿同一方向运动,A以10m/s的速度匀速前进,B以2m/s2的加速度从静止开始做匀加速直线运动,A、B再次相遇前,它们的间距变化情况是( ).
A.一直增大 B.一直减小
C.先增大后减小 D.先减小后增大
在学生的答案中,选择B的占60%以上,理由是“因为在日常生活的追打吵闹中获得了成功,所以只要去追,就应该缩小距离”.答案是C.
1.2 习题“惯性”负迁移
学生在相近或相关问题上多次获得成功的基础上形成了“惯性”,形成一种主观的、僵硬的、带有顽固性的心理准备,把思维限制在狭窄的通道上,得到错误的结论.
例4 在针对“例1”讲解后,为了巩固学生正确的解题思维过程,就问“那么,小球再次被弹出过程中,速度和加速度又如何变化呢?”引导学生再次从小球的受力分析、加速度大小和方向的变化以及与速度方向的关系分析,得到相同的结论,即“加速度先小后大,速度先大后小”.这时,部分学生很快从中总结得出“速度变化总是先大后小,而加速度的变化趋势总是与之相反”.
例5 一个物体从倾角为37°、足够长的斜面上水平抛出,初速度为10m/s,经过多长时间,物体离斜面最远?
为了分解难点,引导学生先解决另一个问题:物体被抛出,到达离斜面最远点时,有什么特点?学生们很快说出“速度为零”,其理由是“物体由于惯性冲上斜面的运动和竖直上抛相似,在最高点的速度都是零”.而正确的说法是:物体到达离斜面最远点时,其速度在与斜面垂直方向上的分量为零,与斜面平行方向上的分量不一定为零.
2 克服思维障碍的对策
2.1 一题多变
通过对某一题目进行图形变换、条件变换、结论探索、类比等多角度和多方位的探究,使一道题变为一类题,达到举一反三、触类旁通的目的,培养学生良好的思维品质.为克服例4中出现的思维障碍,笔者运用了如下变式.

图2
变式1:把例1中的弹簧和小球相连,倒置在升降电梯中(如图2),当电梯带着弹簧和小球匀速上升后,电梯突然停住,小球由于惯性压缩弹簧,那么在小球压缩弹簧的过程中,小球的加速度和速度大小如何变化?学生答:小球的加速度大小一直增加,速度一直减小.
变式2:在变式1中,电梯突然停止后改为突然加速上升,且做匀加速运动,小球由于惯性拉伸弹簧,那么在小球拉伸弹簧的过程中(设弹簧在弹性限度内),小球的加速度和速度大小如何变化?学生答:小球的加速度大小先增加后减小,速度一直增加.
变式3:各题中小球的动能、重力势能及弹簧的弹性势能如何变化?
通过变式3,引导学生比较各题中的能量变化情况,归纳出解决问题的步骤:先确定研究对象,然后进行受力分析,确定合外力大小、方向的变化,以及合外力(加速度)方向与物体初始运动状态的关系,最后得到物体运动状态的变化或能量变化的结论.
2.2 一题多解
对同一个问题,鼓励、启发、引导学生在所学知识范围内,尽可能提出不同的解题构想和方法,拓宽学生的思维空间,培养学生发散思维、创新意识.在克服例3中出现的思维障碍,笔者采用了如下做法.
2.2.1 物理分析法
物体A做速度vA=10m/s的匀速直线运动,B做初速度为零、加速度a=2m/s2的匀加速直线运动.根据题意,在开始的一段时间内,A的速度大于B的速度,它们间的距离逐渐变大,当B的速度加速到大于A的速度后,它们间的距离又逐渐变小.
2.2.2 数学极值法
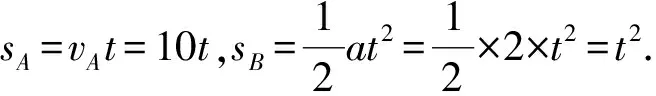
则A、B间的距离Δs=10t-t2,可见,这是一个开口向下的抛物线方程.在t≥0的范围内,Δs是先变大后变小的.
2.2.3v-t图像法

图3
根据题意,作出A、B两物体的v-t图像(如图3),由图可知:A、B再次相遇前它们之间距离有最大值的临界条件是vA=vB,即t1时Δs有最大值,之后Δs又逐渐变小.
解析四:相对运动法
因为本题求解的是A、B间距离的变化,所以可利用相对运动求解.选B为参考系,则A相对B的初速度、末速度、加速度分别是v0=10m/s、vt=vA-vB=0、a=-2m/s2.因此,A相对B先做匀减速远离运动,减速到零后,再反向匀加速靠近,即Δs先变大后变小.
2.3 生活类比法
对于一些极为陌生、抽象的物理概念或规律,用熟悉的、形象化的生活事例去类比,那么往往会产生“一语道破天机”的惊人作用,帮助学生加速认识.例如,在解决例3中出现的思维障碍,笔者这样进行教学.
教师问:你有没有这样的经历,你的某科成绩落后于你的同学,你经过一段时间的努力和追赶,取得了进步(学生基本上答“有”)?教师接着问:那么,你们的差距是变大、不变还是缩小了(学生回答不一)?教师引导学生分析得出结论:自己进步的同时,同学也可能在进步,各自的进步程度不同,导致差距变化不同.由此类比到例3的追及问题,这样类比,可以使学生领略“类比”这一重要的认识问题的思维方法,既加强了物理与生活间的横向联系,又激发了学生学习的兴趣;既降低了某些物理新知识、新规律的教学难度,又增强了学生学好物理的信心.
2.4 假设法
当某一变化因素的存在形式限定在有限种可能时,假设该因素处于某种情况,并以此为条件进行推理的方法,它是科学探究中的重要思想方法,是一种创造性的思维活动.通过对假设状态的分析、判断,使物理过程进行的情况迅速暴露出来,学生能从错综复杂的诸多因素的“纠缠”中解脱出来,大大缩短了分析和推理的时间,达到化难为易、快速解决物理问题的目的.
2.5 针对性实验
这是一种有目的性的操作实验.学生天生好奇好动,而物理实验有很强的吸引力,让他们观察生动有趣的实验,甚至亲手操作实验,极易唤起他们的直接兴趣,提高他们的注意力,有时出乎他们的意料之外的实验现象,更使他们兴趣盎然、印象深刻.具体措施:让学生近距离接触基本仪器,熟悉基本仪器的使用;让学生独立又熟练地完成实验的操作;逐步培养学生对实验数据的处理能力和对实验结果的分析能力,从而排除日常生活经验的干扰,突破思维障碍.例如,在解决例2中出现的思维障碍,笔者引导学生设计DIS实验来模拟两支队伍的拔河比赛,最后让学生分组处理数据及讨论、归纳实验的结果,反思拔河实例中两个拉力、两个摩擦力的大小关系.
总之,在学生学习过程中,不同程度地存在着各种各样的思维障碍,而造成思维障碍的原因是多方面的,教师应针对学生错误的或模糊的看法以及不合理的思维方式,加强教学的预见性和针对性,帮助学生练好基本功,及时排除他们存在的各种思维障碍,并且在运用中不断巩固、深化、提高思维能力.
参考文献:
黄生功.高中物理教学中学生思维能力的培养.长沙:湖南师范大学,2005.

