高中物理习题常见易错题解浅析
(江苏省南京市天印高级中学,江苏 南京 211100)
习题教学是高中物理教学的重要组成部分,对于高三来讲,它几乎占据整个物理教学的“半壁江山”.在实际的教学过程中发现一部分学生在某些问题上出错,往往不能一次更正,主要原因在于知识并没有完全内化.笔者从高一开始就让学生整理一本自己的错题集,用于复习和巩固易错问题,现依托学生的错题集,对学生错题集上部分力学习题进行归类分析,以期对高三物理教学有所启发.
1 概念理解较模糊,感性思维难过渡
经过一轮学习,学生对高中物理知识有了一定的整体认识,但由于高一、高二时学生思维能力的限制,加上时间因素,造成了不同程度的遗忘,学生对物理概念的理解不很清晰,甚至有偏差,易出现错误.
例1 两互相垂直的力F1和F2作用在同一物体上,使物体运动一段位移后,力F1对物体做功4J,力F2对物体做功3J,则合力对物体做功为:( ).
A.7J B.1J C.5J D.3.5J
学生思路:看到两个互相垂直的力,马上想到了力的合成的平行四边形定则,而后面的数值3和4又使我迅速想到了勾3股4弦5,便毫不犹豫地选了C.
教师点拨:功是标量,而力是矢量,它们遵循着不同的运算法则,即矢量和满足平行四边形定则,而标量和只需求代数和,故选A.
2 规律应用不完整,条件范围欠思考
高中物理中规律相对来说较抽象,而且有一定的适用条件和范围,学生对规律的理解不够深刻、全面,这也是学生易错的重要原因.
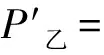
A.m乙=m甲B.m乙=2m甲
C.m乙=4m甲D.m乙=6m甲
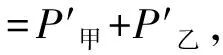

3 题意理解不透彻,关键字句少琢磨
学生大脑中已经形成了不少物理模型,不少习题也在学生的大脑中形成较深的印象,这就极易形成思维定势,对学生的解题产生负面影响.
例3 一根轻质弹簧悬挂在横梁上,在竖直方向上呈自然状态,现将一个质量为0.2kg的小球轻轻地挂在弹簧下端,在弹力和重力的共同作用下,小球做振幅为0.1m的简谐运动,设振动的平衡位置处为重力势能的零势面,则在整个振动过程中弹簧的弹性势能的最大值为多少?系统的总机械能为多少?
学生思路:弹簧伸长量最大时弹性势能最大,即在最低点时弹簧有最大弹性势能,由机械能守恒定律可知:Epm=2mgA=0.4J.弹簧和小球在振动的过程中总机械能等于最大弹性势能,所以E=EPm=0.4J.
教师点拨:对于水平方向的弹簧振子,最大弹性势能等于总机械能,但该问题是在竖直方向,还涉及到重力势能,不能随便套用.小球在初始位置时的机械能为E=mgA=0.2J.
4 对象选取欠灵活,思考角度常单一
在多体问题中,研究对象的合理选取往往决定了解题的繁易,甚至直接影响到结果的得出.学生的思维不够灵活,不注意研究对象的转换,从而造成错误.
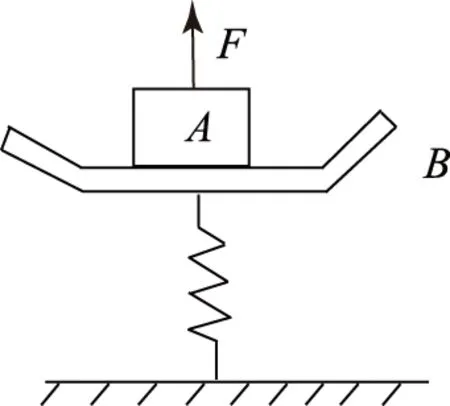
图1
例4 如图1所示,物体A静止在台秤的秤盘B上,A的质量mA=10.5kg,B的质量mB=1.5kg,弹簧的质量忽略不计,弹簧的劲度系数k=800N/m,现给A施加一个竖直向上的力F,使它向上做匀加速直线运动.已知力F在t=0.2s内是变力,在0.2s后是恒力,求F的最大值与最小值.
学生思路:分析A、B的运动情况可知:在t=0.2s时,A、B间的作用力为零,此时弹簧的作用力为F1,F1=kx1,F1-mBg=mBa.

A、B向上运动的过程中,B对A的作用力越来越小,因此在在t=0.2s时,F最大,由牛顿第二定律得:Fmax-mAg=mAa,解得Fmax=168N.开始时F最小,同理可得Fmin=mAa,Fmin=63N.
教师点拨:学生的解题思路基本清楚,但在最后求最小拉力Fmin时出现错误,当加上力F的瞬时,B对A的支持力发生了变化,不再等于A的重力.此时可把研究对象转换为A、B整体,因为弹簧的弹力不能产生瞬时变化,所以有:Fmin=(mA+mA)a=(10.5+1.5)×6N=72N.在分析问题时应注意研究对象的转换,这样在遇到问题时往往会有“柳暗花明”的感觉.
5 参考系选取不当,相对运动出混乱
中学物理研究的通常是在惯性系中的问题,物理规律的应用应相对于同一参考系,不能混淆.参考系的合理选取不仅有利于问题的解决,有时还能使问题得以简化.相反选取不当,也极易造成运动关系混乱.
例5 如图2所示,以速度v匀速行驶的列车车厢内有一水平桌面,桌面上的A处有一个水球沿图中虚线从A运动到B,则由此可判断列车( ).

图2
A.减速行驶,向北转弯
B.减速行驶,向南转弯
C.加速行驶,向南转弯
D.加速行驶,向北转弯
学生思路:据日常生活经验小球向北偏,则车向南转弯,小球向前运动,是因为小车向前加速行驶,故选C.
教师点拨:我们看到的小球桌面的轨迹是小球相对于桌面的运动情况.而车厢的运动是相对于地面,它们的参考系不同,不能看成是同一个参考系.小球由于惯性向前运动,在忽略阻力作用时可近似看成是匀速直线运动,故车厢的相对于小球的运动可看成相对于地面的运动,所以车厢的加速度向后,且向南偏转,即减速行驶、向南转弯.
6 受力分析多忽视,错误经验易干扰
受力分析是解决物理问题的关键,虽经过两年的学习,学生在受力分析这一关上吃的亏仍不少,主要问题是基本功不扎实和缺少受力分析的意识.
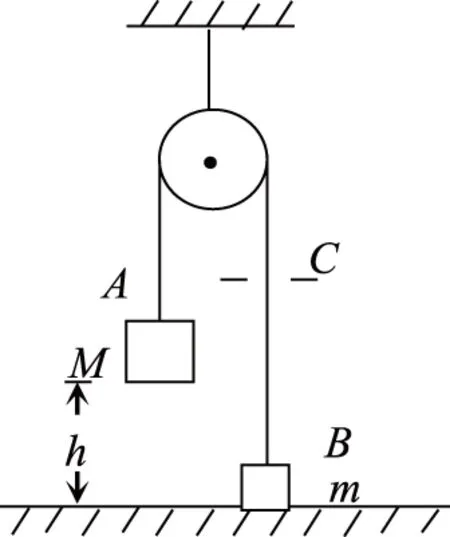
例6 如图3所示,三角形斜劈B静止在光滑水平面上,在斜劈的顶端轻置一个物块A,A物滑到三角形斜劈的底端,已知mA 图3 C.斜劈对A的支持力做了负功 D.斜劈B的斜面愈光滑,分离时B的速度愈大,位移也愈大 学生思路:由水平方向的动量守恒和人、船模型,易得A、D错误,B正确.由于斜劈对A的支持力不做功,故C错误. 教师点拨:分析C选项时,学生受到了错误经验的干扰,即“支持力不做功”.从力的角度去考虑(如图4),可以看出力FN和位移s的夹角大于90°,显然支持力做负功;从能量角度看,若支持力不做功,则A的重力势能全部转化为A的动能,而题中有一部分能量转化为B的动能,对A必有其他力做负功,此力显然为支持力. 图4 物理过程的分析是解题的核心,不少同学不注重过程的分析,往往根据经验,或套用公式导致错误,这在综合题的求解中较为常见. 图5 例7 如图5所示,质量为M的物体A用托板托着,抽走托板后,它将通过绕过定滑轮的绳牵引质量为m的物体B上升,已知m 高中物理解题方法较多,常见的有数学方法、极限分析法、比较法、近似处理法、图示法等,学生在运用这些方法时往往缺少对题意的进一步揣摩和分析,所用方法不恰当,从而造成错误. 图6 例8 如图6所示,质量为m的物块通过细线AO、BO悬于O点,OB与竖直方向的夹角θ=30°,物块处于静止状态.现保持O点的位置不变,OB绳方向不变,使OA绳在竖直平面内缓慢转到竖直方向,OA、OB在水平和竖直位置绳中的张力为多少?此过程中OA、OB绳中的张力如何变化? 学生思路:水平位置时OA绳中张力FA=mgtan30°,OB绳中张力FB=mg/cos30°;而在竖直位置时FA=mg,FB=0.故在OA绳转动过程中,FA逐渐变大,FB逐渐变小. 图7 教师点拨:学生在判断绳中张力变化时运用了极限思维方法,但没有注意到绳OA中的张力不是简单地单调递增,从而出现了错误.该处可用作图法(如图7),可较直观地判断出FA先减小后增大. 图8 例9 如图8所示,有面积很大的水池,水深为H,水面上浮着一个正方体木块,木块边长为a,密度为水的密度的一半,水的密度用ρ水表示,开始时木块静止,现用力F将木块缓缓地压到池底,不计摩擦.求: (1)从木块刚好完全没入到停在池底,池水势能的改变量. (2)木块从开始下降到刚好完全没入的过程中,力F做的功. 学生思路:(1)水面很大,木块没入到池底的过程中水位差可忽略,故ΔEp=0. 教师点拨:第(1)问是“从木块没入”到“停在池底的过程”,这一过程池水的整体水位高度并没有变化,但局部水位发生了变化,即木块和池底等体积的水位置互换,故ΔEp=m水g(H-a)=ρ水ga3(H-a).这里一定要在弄清题意的基础上用等效法处理,而不能不加分析地根据“水面很大”就用近似处理法. 第(2)问中合理地运用了近似处理法,计算出木块的位移.还可以在此基础上运用图象法、等效法算出力F的功. 在考试中因解题欠规范而失分的不在少数,因此良好的解题习惯对学生来说非常重要.一些同学认为只要考试时认真一点,就不会有问题,这种想法极不正确,因为好的习惯不是一天两天培养出来的,需要长期的积累和训练.常见的问题有列式不规范、符号使用不规范、无文字说明等. 笔者建议对错题分析应引起足够的重视,学生要整理,教师更要归类和分析.高三如此,基础年级也应从点滴做起,只有这样才能进一步深入了解学生,真正做到以学生为主体,有的放矢,提高习题教学效率. 参考文献: 刘世军. 通过习题教学培养学生直感思维能力的探讨 .物理之友,2014,30(1). 邵友娣.关于习题教学有效性的思考 .物理之友,2014,30(6).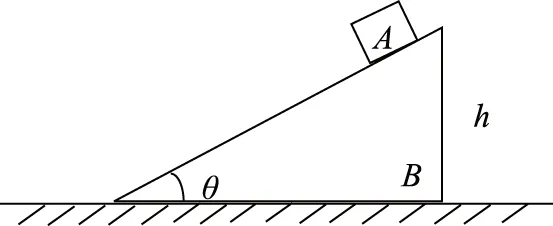
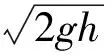

7 过程分析不到位,转换位置易出错
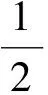

8 解题思路不严密,所用方法欠妥当


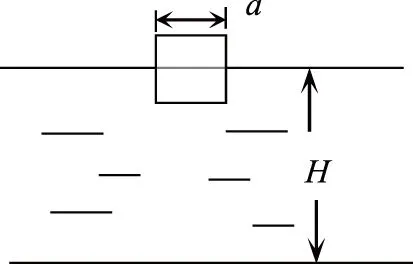
9 解题习惯有欠缺,规范训练须加强

