回旋加速器教学中应该注意的几个问题

(北京市第三十五中学高中部，北京 100032)

在教学中笔者发现，对回旋加速器原理的定性描述学生容易理解，而根据回旋加速器原理进行的定量分析，学生暴露出的问题比较多，具体体现在关于回旋加速器的同步问题、做功问题、动能问题的细节之中.现结合问题进行具体的分析讨论，并给出教学的相关建议.

例1 在高能物理研究中，粒子回旋加速器起着重要作用，如图1为它的示意图.它由两个铝制D型金属扁盒组成，两个D型盒正中间开有一条窄缝，两个D型盒处在匀强磁场中并接有高频交变电压.图2为俯视图，在D型盒上半面中心S处有一正离子源，它发出的正离子经狭缝电压加速后，进入D型盒中.在磁场力的作用下运动半周，再经狭缝电压加速.如此周而复始，最后到达D型盒的边缘，获得最大速度，由导出装置射出.已知正离子的电荷量为q，质量为m，两板间电压最大值为U，磁场的磁感应强度为B，D型盒间距离为d，半径为R.每次加速的时间很短，可以忽略不计.正离子从离子源出发时的初速度为零.

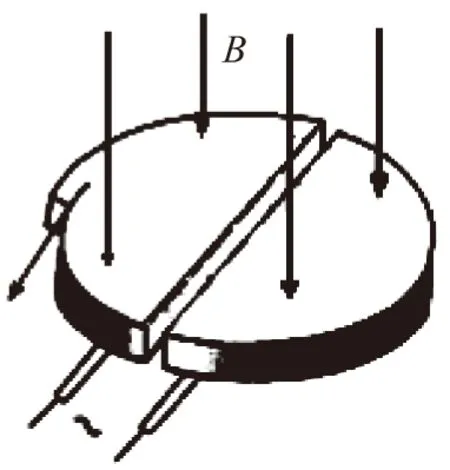
图1

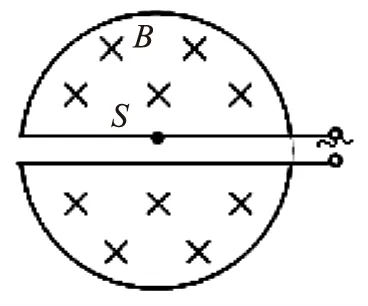
图2

(1)为了使正离子每经过窄缝都被加速，求交变电压的周期；

(2)每次加速所增加的动能；

(3)求离子能获得的最大动能；

(4)加速到上述能量所需时间为多少．

1 回旋加速器的“同步”问题

从题目的信息中可知：带电粒子经狭缝电压加速后，在磁场中运动半周，随后经狭缝处电场加速，再在磁场中运动半周——如此周而复始，最后到达D型盒的边缘，获得最大速度.

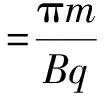
2 回旋加速器的“做功”问题

交变电场对某个带电粒子做功该如何计算呢？“每次加速的时间很短，可以忽略不计”，题目中已明确说明.即每次加速过程，电压恒定，电场力做功W=qU.

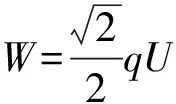
3 回旋加速器的“动能”问题

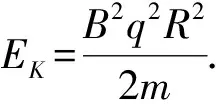
若一次加速就把动能增大到所需要的数值，就必需加速电压足够大.如此高的电压，其一是技术上不易做到，其二是即使能够提供高电压，由于电压过高，两极间电场太强，两极间介质容易被击穿放电.因此，一般采用低电压多次加速.回旋加速器就是采用这种方法.

那么，为什么回旋加速器粒子的最大动能却与加速电压无关呢？这是因为回旋加速器半径R一定.若加速电压较高，每次加速动能(速度)增加的快，磁场中回转半径增加的快，这样，经过很少的加速次数，回转半径就可达到回旋加速器半径R；若加速电压较低，每次加速动能(速度)增加的慢，磁场中回转半径增加的慢，经过很多的加速次数，回转半径仍可达到回旋加速器半径R，所以最大动能与加速电压无关.

综上所述，在指导学生学习中，帮助学生明白以上几个问题，学生就能很好的理解回旋加速器的原理.以上过程充分体现了对细节和思维过程的关注，这一做法值得在物理问题解决中推广贯彻.

4 回旋加速器中的“时间”问题

参考文献：

[1]胡扬洋，陈清梅，邢红军.中国物理变式教学研究：传统与发展[J].教育导刊，2014，(2).

[2]胡扬洋，石尧.由一道“北约”物理题的三种解法看自主招生备考[J].物理教学，2013，(12).

[3]陈清梅，胡扬洋，邢红军.物理高端备课：构建U-S合作的桥梁——以“生活中的圆周运动”为例[J].教育科学研究，2013，(12).

[4]邢红军，陈清梅，胡扬洋.科学方法纳入《课程标准》：基础教育课程改革的重大理论问题[J].教育科学研究，2013，(7).